基于曲率模态法识别轨道板的伤损研究

胡志鹏，刘婷林，谢铠泽，王 平

(西南交通大学高速铁路线路工程教育部重点实验室， 成都 610031)

基于曲率模态法识别轨道板的伤损研究

胡志鹏，刘婷林，谢铠泽，王 平

(西南交通大学高速铁路线路工程教育部重点实验室， 成都 610031)

无砟轨道轨道板在施工和运营中存在空洞及裂缝等伤损，伤损的出现会改变结构的动力学特性，由模态分析理论可知，系统特性的改变必然会引起模态参数的改变。建立轨道板-砂浆有限元模型，通过单元刚度的折减来模拟轨道板单处伤损和多处伤损，运用曲率模态识别伤损的方法对轨道板横向和纵向分别进行曲率模态计算分析。计算结果表明：轨道板横向和纵向任一方向的曲率模态和曲率模态差都能准确的识别出伤损位置，并且可以依据这两个指标识别出轨道板的多处伤损。

轨道板；CA砂浆；伤损；曲率模态；曲率模态差

无砟轨道以其稳定性好、耐久性好、平顺性高、少维修的特点在国内迅速发展。但随着无砟轨道的运营，各种损伤病害相继出现，轨道板、砂浆、支撑层等都出现不同类型不同程度的伤损[1]，伤损的出现直接影响列车的安全运营。就轨道板而言，有轨道板中的空洞伤损以及在列车荷载和外界环境作用下的裂缝伤损。伤损的出现会改变结构动力学特性。由模态分析理论可知，系统特性的改变必然会引起模态参数的改变。利用曲率模态来识别结构的伤损已在桥梁伤损识别中取得很好的效果，能够准确找出伤损位置[2-6]。文献[7-10]已经介绍了曲率模态在板式结构中伤损识别的应用，在此基础上对轨道板伤损进行曲率模态分析，并通过刚度的减小来模拟轨道板不同的损伤工况。

1 理论背景

由于轨道板的厚度比其长度和宽度小很多，轨道板在垂向可视为弹性薄板，薄板的受弯分析采用如下假定[11]：

(1)薄板的法线没有伸缩；

(2)薄板的法线在薄板弯扭后仍保持薄板弹性曲面的法线[6]。

基于上述假定，本文在研究过程中只考虑轨道板的弯曲变形。由材料力学知识可知，直梁曲率与弯矩M之间的关系为

式中，M(x) 为截面x处的弯矩;EI为截面抗弯刚度;k为曲率。

从式(1)中可以看出，曲率与刚度成反比，刚度的变化会引起曲率的变化。如果轨道板局部出现裂缝或其他伤损，则会引起相应部位刚度的变化，使得该处的曲率也发生变化。由于现阶段没有直接能测出结构曲率模态的仪器，通过有限元离散模型的振动模态分析，计算出等间距有限元离散单元节点处的位移模态，则结构的曲率模态可由中心差分方程求出

式中，h为单元长度；φi,j为第i阶模态在第j个节点处垂直方向位移。

对于梁式结构，一般求取中性轴的曲率模态，而板式结构，则需分别求解出x，y两个方向的曲率模态，并计算出曲率模态差，用这两个指标来判断伤损的有无以及伤损的具体位置。

2 模型建立

利用有限元软件进行建模分析，建立轨道板-CA砂浆模型，轨道板采用shell63单元模拟，砂浆采用combin14弹簧单元模拟。轨道板参数为：弹性模量E=3.65×104MPa，密度为2 500 kg/m3，泊松比为0.2；砂浆E=300 MPa；轨道板长度4.8 m，宽2.4 m。横向划分12份，纵向划分24份。

轨道板的伤损采用单元刚度的降低来模拟，如图1所示。轨道板四周及砂浆底部采用全约束，如图2所示。分析单处损伤和多处损伤两种工况下的曲率模态，伤损单元如图3所示。由于篇幅有限，本文只分析一阶曲率模态。

图1 轨道板-砂浆伤损模型图2 轨道板-砂浆伤损边界约束图3 有限元单元及伤损单元

3 数值仿真分析

伤损单元及伤损程度如表1所示，计算固有频率的变化及x方向和y方向一阶曲率模态、曲率模态差。

表1 伤损单元及伤损程度

3.1 固有频率伤损识别

轨道板模态分析中，固有频率是一个比较容易计算的参数，结构的损伤通常会引起质量矩阵和刚度矩阵的变化。由于在轨道结构中，质量分布基本不变，损伤常常使得结构的刚度降低。表2为轨道板-CA砂浆结构无损伤、单处伤损和多处伤损的前5阶固有频率。从表中可以看出，轨道板的伤损引起了固有频率的变化，但有些模态阶数的固有频率变化很微小，反映不出结构伤损，并且固有频率的变化也无法判断出伤损的具体位置，因此基于固有频率的变化在轨道板伤损判别中无实际意义。

3.2 曲率模态和曲率模态差伤损识别

通过计算无损伤、单处伤损及多处伤损的曲率模态和曲率模态差来识别伤损位置。仅取第一阶模态振型进行分析，图4～图15为3种工况下的曲率模态和曲率模态差计算结果。

表2 无损伤、单处伤损和多处伤损的固有频率 Hz

(1)无损伤、单处损伤曲率模态及曲率模态差

从图4可以看出，轨道板无损伤工况在x方向曲率模态图形较平滑，没有出现峰值。图5中，轨道板的x方向曲率模态在中间位置出现一明显峰值，并且该峰值对应区域也正是损伤预设位置，这说明利用单一方向的曲率模态可以判断出伤损及伤损位置。图6为一阶曲率模态差，在中间位置明显出现一尖峰，很容易判断出伤损位置，且伤损位置与预设伤损位置相符。

由图7可以看出轨道板在y方向无损伤时曲率模态曲线平滑。图8中轨道板一阶曲率模态中间区域出现尖峰，曲率模态发生明显突变，表明轨道板存在伤损且伤损位置与尖峰所处区域一致。图9曲率模态差很明显地反映出了伤损的存在及具体位置。比较x、y方向曲率模态及曲率模态差可以看出，y方向更能明显地反映出伤损及伤损的位置。

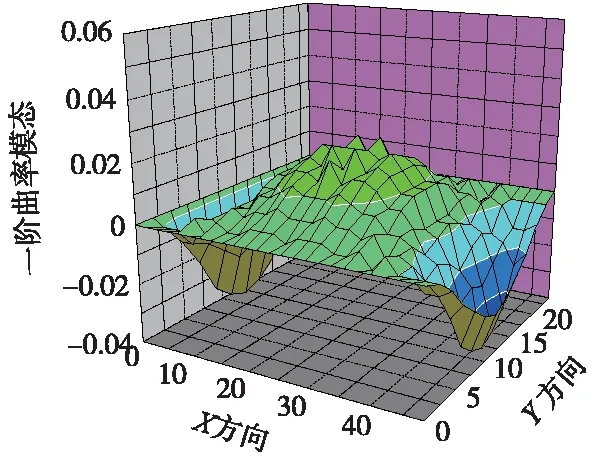
图4 x方向无损伤一阶曲率模态

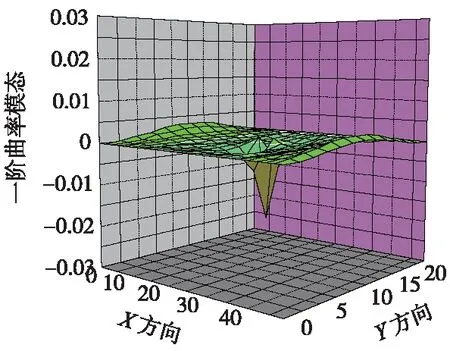
图5 x方向单处损伤一阶曲率模态

图6 x方向一阶曲率模态差

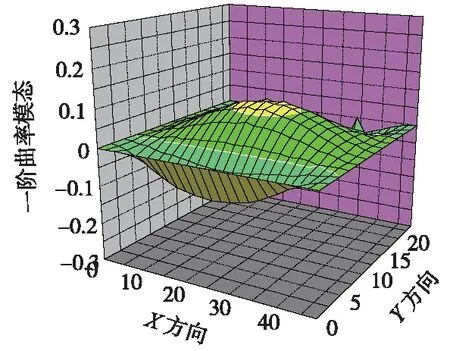
图7 y方向无损伤一阶曲率模态

图8 y方向单处损伤一阶曲率模态

图9 y方向一阶曲率模态差

(2)无损伤、多处损伤曲率模态及曲率模态差

从图10～图12可以看出，当轨道板存在多处伤损时，其x方向的一阶曲率模态存在明显的两个峰值，可以判断出伤损的具体位置。x方向的曲率模态差也能明显地反映出伤损的具体位置，说明这两个指标都能判断轨道板的伤损有无以及伤损具体位置。

图10 x方向无损伤一阶曲率模态

图11 x方向多处损伤一阶曲率模态

图12 x方向一阶曲率模态差

图13 y方向无损伤一阶曲率模态

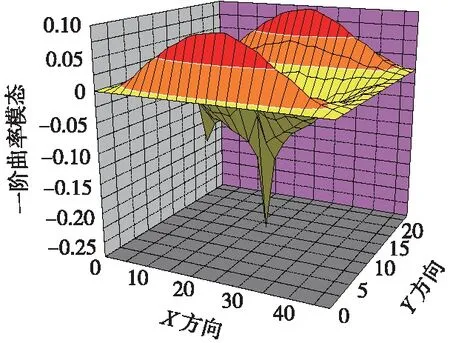
图14 y方向单处损伤一阶曲率模态

图15 y方向一阶曲率模态差

由图13～图15可以看出，y方向的一阶曲率模态和曲率模态差出现2个峰值，反应出轨道板的多处伤损位置。通过x，y方向分别计算的曲率模态和曲率模态差结果来看，两个方向都能识别出伤损位置，x方向伤损识别较y方向明显。在工程实际中，由于结构无损伤的参数不容易得到，因此还得依靠曲率模态来识别伤损，上述计算结果表明，只用曲率模态也可以很准确地识别伤损及伤损具体位置。

4 结论

(1)通过计算轨道板x，y方向的曲率模态和曲率模态差，其中x和y任意一个方向的曲率模态值变化都可以准确识别轨道板伤损的位置。

(2)从轨道板伤损的曲率模态结果来看，曲率模态可以很好地识别轨道板的伤损；由于轨道板伤损前的参数不容易得到，因此对轨道板伤损识别时可以只用曲率模态值进行判断。

(3)曲率模态法不仅可以准确识别轨道板单处伤损，还可以准确地识别轨道板的多处伤损。

[1] 魏祥龙，张智慧.高速铁路无砟轨道主要病害(缺陷)分析与无损检测[J].铁道标准设计，2011(3):38-40.

[2] 李德葆，陆秋海，秦权.承弯结构的曲率模态分析[J].清华大学学报，2002，42(2):224-227.

[3] Pandey A K， Biswas M. Samman M.Damage detection from changes in curvature mode shapes[J]. Journal of Soundand Vibration， 1991，145 (2):321-332.

[4] 陈江，熊峰.基于曲率模态振型的损伤识别方法研究[J].武汉理工大学学报，2007，29(3):99-102.

[5] 王静，张伟，王骑，等.基于曲率模态法的简支板桥损伤识别研究[J].工业建筑，2006(S1 ):225-227.

[6] 白羽.梁-板-网架结构损伤诊断研究[D].昆明：昆明理工大学，2008：28-33.

[7] 李建康，张春利，解辛辛.板类结构动力检测与控制中的一种新方法[J].动力学与控制学报，2005，3(3):73-77．

[8] 何钦象，杨智春，姜峰，田小红.薄板损伤检测的高斯曲率模态差方法[J].振动与冲击，2010，29(7):112-115．

[9] 张波，王赟，姜峰.基于曲率模态差的四边固支薄板的损伤检测[ J ].河北工程大学学报，2009，26(3):31-36．

[10] 沈庆阳，纪国宜.基于曲率模态的薄板结构的损伤定位研究[ J ].工业建筑，2013，(S1)：322-326．

[11] 刘学毅，赵坪锐，杨荣山，王平，客运专线无砟轨道设计理论与方法[M].成都：西南交通大学出版社，2010:56-85．

Study on Damage Identification of Track Slab Based on the Curvature Modal

HU Zhi-peng， LIU Ting-lin， XIE Kai-ze， WANG Ping

(MOE Key Laboratory of High-speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China)

Hollows and cracks develop in ballastless track slab during construction and operation. The occurrence of the damages will change the system dynamic characteristic. The modal analysis theory shows the change of the system characteristics will inevitably change the modal parameters. This paper illustrates the process to establish the finite element model of track slab-mortar， and to simulate single damage and multi damages of track slab by means of stiffness reduction of element. The calculation and analysis of curvature modal in transverse or longitudinal direction of track slab is conducted with the method of curvature modal damage identification. The results show that the curvature modal and curvature modal difference in either transverse or longitudinal direction of track slab can locate a single damage and multiple damages of track slab can also be identified.

Tack slab; CA mortar; Damage; Curvature modal; Curvature modal difference

2013-12-09；

：2013-12-13

四川省科技支撑计划项目(2012GZ0104)

胡志鹏(1990—)，男，硕士研究生，E-mail：779355629@qq.com。

1004-2954(2014)09-0052-03

U213.2+44

：A

10.13238/j.issn.1004-2954.2014.09.013