机载雷达告警系统中威胁等级判定方法研究

周 帆, 封吉平, 赵 喜, 韩壮志

(军械工程学院 电子与光学工程系，河北 石家庄 050003)

0 引 言

威胁等级判定是现代机载雷达告警系统中的一个重要内容，尤其是在实时的告警干扰应用中，对威胁程度不同的多个辐射源，实施不同优先等级的干扰措施才能达到最佳的干扰效果[1]。威胁等级判定是根据辐射源的技术参数、工作状态等指标，估计其危害能力和作战意图，通过加权处理，按照辐射源产生的威胁对我方可能造成的危害程度进行分类[2]，并考虑实战应用的特点，判定其所属的威胁等级。要判定辐射源的威胁等级，须从3个方面确定：威胁指标隶属度模型、威胁指标权重以及辐射源威胁等级判定函数。

本文首先通过分析威胁辐射源技术参数和工作状态的特点，建立了威胁指标隶属度模型；然后利用综合赋权法融合了主客观权重，获得了各个威胁指标的权重,并且依据作战飞机实际作战时对雷达告警系统的性能要求，建立了相应的威胁等级判定函数；最后通过应用举例证明了本文所提出的威胁等级判定方法的有效性。

1 威胁指标隶属度模型

在辐射源众多技术参数中，用于威胁等级判定的参数为脉冲载频(RF)、脉冲宽度(PW)和脉冲重复周期(PRI)，依次记为T1，T2，T3，加上辐射源的工作状态T4，记T={T1，T2，T3，T4}。这4个威胁指标的量纲和数量级各有不同，有的参数越小，威胁程度越小，还有的参数则要稳定在确定范围。利用模糊数学中的隶属程度，建立相应的隶属度函数，便可统一各威胁指标不同的要求，避免了运用精确数学处理此类问题时的不便[3,4]。

1.1 脉冲载频隶属度模型

一般的，辐射源发射的脉冲信号的载频范围为300 MHz～300 GHz，其中绝大多数脉冲载频集中在L,S,C,X,Ku 5个波段。脉冲多普勒雷达通常多工作在Ku或X波段，属于精密火控跟踪雷达，威胁等级最高，隶属度取值为1；辐射源工作在S或C波段时，威胁程度比较大，隶属度取值为0.7；辐射源工作在L波段时，威胁程度相对较小，隶属度取值为0.4；由于工作在其他波段的辐射源相对较少，隶属度取值为0.2。脉冲载频隶属度函数为

(1)

1.2 脉冲宽度隶属度模型

通常，脉冲宽度T2的取值范围0.1～200 μs，脉冲宽度越窄，测距精度越高，威胁程度越高，故精密跟踪雷达常采用很窄的脉冲。脉冲宽度隶属度函数可选为

u(T2)=

(2)

其中，k=0.000 5 。

1.3 脉冲重复周期隶属度模型

雷达的脉冲重复周期T3的大致范围为100～10 000 μs，且脉冲重复周期越小，威胁程度越大。精密的火控跟踪雷达通常都采用小的脉冲重复周期，以便能精确地跟踪打击目标。因此，脉冲重复周期隶属度函数可选为

u(T3)=

(3)

其中,k’=5 。

1.4 辐射源工作状态隶属度模型

对于作战飞机而言，辐射源的工作状态通常分为制导、跟踪、引导和搜索四种。辐射源工作状态在制导时的威胁程度最高，隶属度取值为1；其次为处于跟踪状态时，隶属度取值为0.75；再次为处于引导状态时，隶属度取值为0.5；威胁程度最小的是搜索状态下的辐射源，隶属度取值为0.25。辐射源工作状态隶属度模型为

(4)

2 威胁指标权重确定

不同威胁指标在辐射源威胁等级评定过程中存在着客观差别，弥补这些差别的方法是规定不同指标在威胁等级判定中的权重，以权重体现不同威胁指标在威胁等级判定中的差别[5]。

目前确定指标权重的方法主要有两类，第一类为主观赋权法，如专家调查法、层次分析法(analytic hierarchy process，AHP)和Delphi法[6]；第二类为客观赋权法，如因子分析法、熵值法[7]和重要性排序法。两种方法各有优点，但又各有缺点。为了兼顾专家对威胁指标重要的经验认知和战场环境提供的威胁指标重要性的客观信息，本文采用层次分析法获得各威胁指标的主观权重，用熵值法获得各威胁指标的客观权重，最后用综合赋权法对主客观权重进行融合，确定各威胁指标的综合权重。

2.1 威胁指标主观权重的确定

层次分析法是将与决策有关的指标分解成目标、准则、方案等层次，在此基础上进行定性和定量分析的方法。该方法是匹兹堡大学教授萨蒂(Satty T.L.)提出的。

对4个威胁指标T={T1，T2，T3，T4}构建层次结构图，如图1所示。在图1中目标层A的目的是合理确定各威胁指标的权重，指标层T包含4个威胁指标。

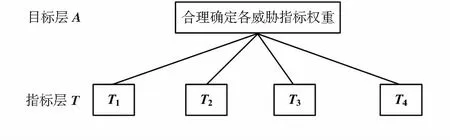
图1 确定各威胁指标权重的层次结构图

根据专家的先验认知，得到威胁指标两两之间重要性比较的判定矩阵

(5)

矩阵中amn表示威胁指标m较威胁指标n的重要性之比，且满足amn和anm互为倒数，amn取值为1时，表示2个威胁指标同等重要。

由于专家给出判定矩阵时具有一定的主观性，判定矩阵中的元素并不一定严格遵守数学规律，使得矩阵往往不能达到一致性的要求。一致性是指矩阵中的元素满足如下关系式

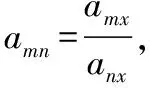
(6)

利用最优传递矩阵改进型的层次分析法[8]构造判定矩阵A的拟优一致阵便可解决上述问题。设矩阵B，使得bmn=lgamn，求出矩阵B的最小偏差传递矩阵C，即

(7)

从而可以求出A的拟优一致阵

A*=10C.

(8)

A*的最大特征值的特征向量为

(9)

归一化后，即可得到威胁指标的主观权重

(10)

2.2 威胁指标客观权重的确定

熵(entropy)是指体系的混乱程度，在不同的学科中也有引申出的更为具体的意义，是各领域十分重要的参量。熵由鲁道夫·克劳修斯(Rudolf Clausius)提出，最早应用在热力学中,后来，克劳德·香农(Claude Shannon)第一次将熵的概念引入到信息论中。熵值法是一种根据各项指标观测值所提供的信息量的大小来确定目标权重的方法[9]。

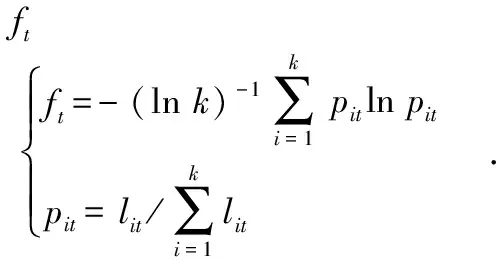
(11)

当pit为0时，pitlnpit为0。

威胁指标Tt的客观权重为

(12)

通过上式计算即可得到威胁指标的客观权重

(13)

2.3 综合权重的确定

建立如下的优化模型

(14)

其中,ρ为偏好系数，它由决策者对主客观权重的偏好程度而设定，取值范围为(0，1)。

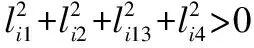
(15)

且威胁指标的综合权重满足如下条件

(16)

3 辐射源威胁等级判定函数的建立

不同辐射源的威胁程度差别较大，如跟踪雷达比警戒雷达威胁大，同为跟踪雷达，处于跟踪状态时的威胁程度大于处于搜索状态时。辐射源的参数和工作状态与辐射源的威胁程度有着密切的关系。根据作战飞机通常的实战环境，主要的威胁辐射源有警戒引导雷达、火控雷达以及各种由无线电制导的防空导弹等。根据机载雷达告警系统综合性能要求，将威胁等级级别分为七级，一级威胁程度最高，七级威胁程度最低。辐射源威胁等级判定函数为

(17)

设某辐射源各威胁指标的隶属度为L(lt)1×4，将其与综合威胁权重W相乘，便可得到该辐射源的综合威胁度Z，即

(18)

将综合威胁度Z与辐射源威胁等级判定函数对比，便可知道指定辐射源的威胁等级。

4 应用举例

首先，让专家对4个威胁指标在威胁等级判定中的重要性进行估计与评价后，给出的重要性判定矩阵为

(19)

由式(7)和式(8)得出A的拟优一致阵A*为

(20)

由式(9)和(10)可以得到威胁指标的主观权重为

W′=[0.126 0.073 0.248 0.553]T.

(21)

设作战飞机遭遇到了4个威胁辐射源，其技术参数和工作状态见表1。

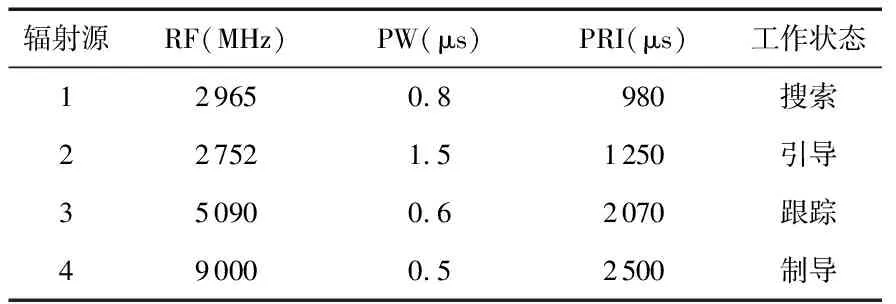
表1 辐射源的技术参数和工作状态

由式(1)～式(4)计算可得这4个辐射源的隶属度矩阵为

(22)

由式(11)～式(13)可以得到威胁指标的客观权重

W″=[0.090 0.011 0.146 0.753]T.

(23)

将偏好系数设为0.6，由式(15)和式(16)得到威胁指标的综合权重为

W=[0.112 0.048 0.207 0.621]T.

(24)

将式(22)与式(24)相乘，便可得到4个辐射源的综合威胁度

Z=[0.414 0.547 0.763 0.959]T.

(25)

将式(25)与辐射源威胁等级判定函数进行对比，可以得到辐射源1的威胁等级为六级，辐射源2的威胁等级为四级，辐射源3的威胁等级为三级，辐射源1的威胁等级为一级，辐射源4的威胁程度最高，辐射源1的威胁程度最低。

5 结 论

本文根据现在作战飞机所面临的作战环境，选取了辐射源的3个技术参数和工作状态作为威胁指标，更加贴近机载雷达告警系统的性能要求。将主客观权重相融合得到各威胁指标的综合权重，即考虑了专家对于威胁指标的先验知识，又使得威胁指标权重可随威胁辐射源和作战环境的动态变化而不断地更新，对于瞬息万变的现代战场有更好的适应性。实例应用的结果表明:本文所提出威胁等级判定的方法对于机载雷达告警系统是可行的、有效的，为机载雷达告警系统中的威胁等级判定提供了新的参考。

参考文献:

[1] 姜 宁,胡维礼,孙 翱.辐射源威胁等级判定的模糊多属性方法[J].兵工学报,2004,25(1):56-59.

[2] 麻士东,韩 亮,龚光红,等.基于云模型的目标威胁等级评估[J].北京航空航天大学学报,2010,36(2):150-153,179.

[3] 刘 清.Rough集及Rough推理[M].北京:科学出版社,2001.

[4] 朱志宁.基于模糊推理的雷达辐射源识别方法[J].火力与指挥控制,2009,34(4):95-99.

[5] 李亚楠.战场侦察警戒信息融合仿真系统及其关键技术研究[D].长沙:国防科技大学,2005.

[6] 郭红玲,黄定轩.多属性决策中属性权重的无偏好赋权方法[J].四川交通大学学报,2007,42(4):505-510.

[7] 陶菊春,吴建民.综合加权评分法的综合权重确定新探[J].系统工程理论与实践,2001(8):43-48.

[8] 李正东.量化目标威胁等级的改进[J].系统工程与电子技术,2003,25(5):563-567.

[9] 滕兆新,杨世兴,傅学庆.基于熵权的布雷作战方案优选[J].火力与指挥控制,2008,33(7):143-145,152.