用于数字D类放大器的双边PWM调制模块

史龙飞，樊养余，吕国云，袁永金，黄伯骅

（西北工业大学 陕西 西安 710129）

用于数字D类放大器的双边PWM调制模块

史龙飞，樊养余，吕国云，袁永金，黄伯骅

（西北工业大学 陕西 西安 710129）

文中介绍了一种双边PWM调制的数字D类放大器调制模块，使用伪自然采样法消除谐波失真。该伪采样算法是将牛顿-拉夫森迭代法和多项式逼近法相结合而形成的。近年来，虽有较多关于前沿PWM调制（LEPWM）和后沿PWM调制（TEPWM）的数字D类放大器的文献，但基于双边PWM（DEPWM）调制的数字D类放大器方面的文献较少。因此本文利用现有的 噪声整形技术，基于牛顿-拉夫森迭代法的伪采样算法等实现了一种用于数字D类放大器的双边PWM调制模块，并使用FPGA搭建了一个24位立体声数字音频D类放大器调制系统。经测试，该调制系统THD+N@6 kHz性能达到-80.5 dB。

数字D类放大器；伪采样PWM调制；双边PWM调制；牛顿-拉夫森迭代法；FPGA

数字D类放大器中PWM调制方式分为单边调制（SEPWM）和双边调制（DEPWM），两种调制方法均有不同程度的谐波失真，但双边调制较单边调制来说具有更小的奇次谐波失真，并且不包含载波的谐波和偶次谐波。然而由于数字D类放大器中的数字PWM调制方式使得调制后的PWM信号的谐波失真大大增加，为了减少谐波失真，需要使用伪自然采样（PNPWM）的方法来逼近自然采样PWM（NPWM），并要依据PWM调制方式制定一定的伪采样算法降低谐波失真。

单边PWM调制只有一个调制边沿，计算过程较为简单，因此有较多调制方法提出[1-3]，而双边PWM调制具有两个调制边沿，不能简单按照单边PWM调制的过程来进行调制。单边PWM调制的伪采样算法也不能直接被用做双边PWM调制，∑Δ噪声整形技术的使用也与单边PWM调制不同。因此，文中介绍了一种基于伪自然采样算法的双边PWM调制模块。

1 双边PWM调制

如图 1，图中 c（t）为三角载波，x（t）为被调制信号，y（t）为调制后的PWM信号。双边PWM调制和单边PWM调制区别在于双边PWM调制的载波为三角波，具有两个调制边沿，调制出的PWM信号的两个边沿均随信号的变化而变化；而单边PWM调制由于其载波为锯齿波，有一个边沿垂直于轴，因此其调制出的PWM信号同样有一个边沿固定，而另外一个边沿随着信号的变化而变化。因此，双边调制较单边调制来说具有更小的奇次谐波失真，并且不包含载波的谐波和偶次谐波。

依据[4]的结论，双边自然采样PWM（NPWM）的频谱可以分解为两个单边NPWM的频谱之差，如式（1）：

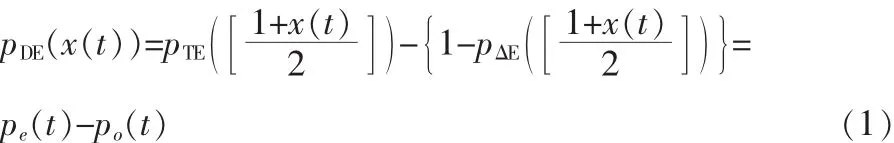
图1 单边和双边PWM调制Fig.1 Single-edge and double-edge PWM modulate

式中，pDE，pLE和 pTE分别为 DEPWM，LEPWM 和 TEPWM信号。如图2所示，DEPWM可以分为两个TEPWM信号，一个由信号和三角波的上升边沿交点决定宽度，另一个由信号和三角波的下降边沿交点决定宽度，最终的DEPWM信号为两个PWM信号之差。

图2DEPWM生成图示Fig.2 DEPWM generation diagram

在生成PWM信号之后，将PWM信号通过低通滤波器（LPF）滤除超出音频范围的频率成分。该过程可以用下面的式子表示：

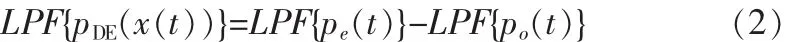
从式（2）可以看出低通滤波器在DEPWM的两个∑Δ部分上均有作用，且相互独立。因此可以分别使用两个调制器对DEPWM的两个部分进行噪声整形，将降低数据位宽造成的量化噪声推移至音频频带以外。

为了生成DEPWM信号，首先需要产生两路连续的采样数据，这两路数据为一个调制周期内 c（t）和 x（t）的两个交点，设为向量xk，该数据应为经过PNPWM模块调整过后的数据。然后分别对两路信号进行∑Δ噪声整形，设生成的低位宽的信号向量为yk。假设∑Δ调制器阶数为n，那么生成的信号在z域的表达式为：

其中Ek（z）为量化误差在z域的表示。

然后，信号经过 PWM 发生器，将所有成分（pe（t），po（t））转换成为 PWM 信号。 而两个信号成分的差值 pDE（x（t））=pe（t）-po（t）即为最终的DEPWM信号。DEPWM信号在时域可以表示为：

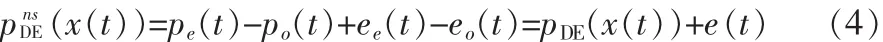
其中 ee（t）和 eo（t）分别为两路信号的量化误差。 和式（4）对应的信号z域表达式为：

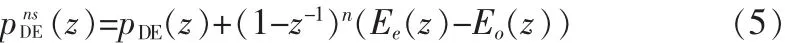
其中pDE（z）为最终DEPWM信号的z域表达式。由此可以看出分别使用两路调制器能够将正确的传递原始的DEPWM信号频率成分，并且将量化噪声推移至音频频带外，经过低通滤波之后能够还原为输入信号。

2 基于牛顿-拉夫森迭代法的伪采样算法

第一部分已经叙述了从∑Δ噪声整形到产生DEPWM信号的相关内容，而∑Δ噪声整形模块需要输入信号，该输入信号可以直接使用过采样之后的信号，但是由于数字信号在单个脉冲周期中保持不变，因此会产生较大的谐波失真[5]。为了消除该谐波失真，普遍采用伪自然采样的方法去模拟自然采样，使数字PWM调制器能够接近模拟PWM调制器低谐波失真的性能。本文利用牛顿-拉夫森迭代法和多项式逼近法实现了一种伪自然采样算法。该算法在一个PWM脉冲周期内使用多项式逼近法近似求出输入信号的表达式，然后使用牛顿-拉夫森迭代法求出信号和载波的交点，由于载波具有两个调制边沿，因此需要分别计算信号和载波两个调制边沿的交点。求出交点后，如第一部分所述，将经过伪采样调整之后的数据分别送入两个∑Δ调制器，最后经过PWM发生器即可得到最终的DEPWM信号。与用于单边PWM调制的为采样算法不同的是，用于双边PWM调制的单个脉冲周期跨越两个采样周期，因此双边PWM调制对原始信号的插值倍数较单边PWM调制要多一倍。

如图 3 所示，输入信号为 in（t），载波信号为 cw（t），单个脉冲周期区间为t0～t2。伪采样算法则要求输入信号in（t）和载波信号 cw（t）的交点，该问题可以转化为求方程 f（t）=cw（t）-in（t）=0的根，假设根为tr。因为能够获得的数据仅为离散的采样点，无法求得方程真正的根，只能求得方程根的逼近值，本文采用牛顿-拉夫森迭代法进行逼近计算。

假设时间轴的间隔为1，即t1-t0=1，载波幅度为-1到1，则载波两边的斜率的绝对值均为2，那么t0～t1之间的载波可以表示为，cw（t）=-2t+1，t1～t2之间的载波可以表示为，cw（t）=2t-1。首先，为了逼近方程f（t）的根，需要一个方程根的预测值作为迭代的初值，为了使得最终迭代结果精确，使用两个采样点连线和载波的交点作为迭代的初值，设为ta。在t0和t1之间，ta的值可以表示为：

然后在ta处使用一次牛顿-拉夫森迭代，得到te，即为较为精确的对tr值的逼近：

式中te的为对方程 f（t）根的估计，即较为精确的对tr值的逼近。将te带入载波方程cw（t）即可求得信号和载波的交点处的幅值。

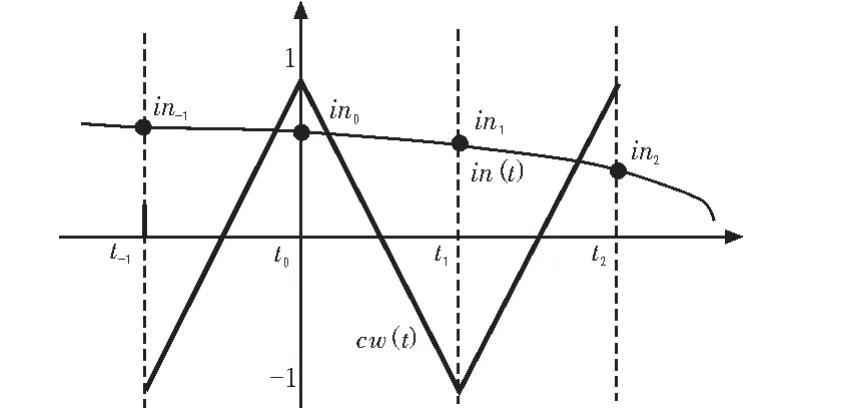
图3 双边PWM调制伪自然采样算法图示Fig.3 Pseudo natural sampling for double-edge PWM modulation

但是式（7）中的 in（t）和 in′（t）均为未知，因此需要对输入信号进行拟合，得到其近似的数学表达式。为了使计算过程不会过于复杂，这里使用三阶的插值多项式逼近，使用4个采样点作为参考点进行计算。假设逼近得到的信号表达式及其一阶微分为 i＾n（t）和 i＾n′（t），方程式 f（t）对应的逼近表达式及其一阶微分为f＾（t）和f＾′（t）。 它们可以表示为：

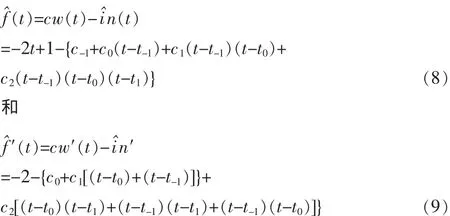
式（8）和式（9）中的多项式系数 ci（i∈{-1，0，1，2}）可以通过将已知采样点的值带入上面的式子中进行计算。可以得到：

至此，将 ta带入式（8）和式（9）即可得到 f（ta）和 f′（ta）的近似值，最终依据式（7）得到方程根的逼近值te，将te带入载波方程cw（t）即可得到交点处信号的幅值。

以上列出了在t0～t1之间（载波三角波的下降边沿）的计算过程，而在t1～t2之间（载波三角波的上升边沿），重新计算系数ci的值，将新的载波方程cw（t）以及信号方程的逼近值带入上述计算过程中即可得到方程根的逼近值，计算过程相似，这里不在赘述。

3 双边PWM调制模块

3.1 调制模块的数值仿真

为了验证调制模块的性能并确定模块的参数，本文首先使用MATLAB进行了数值仿真。图4为构建的调制模块输出频谱仿真结果（输入信号：6 kHz正弦波），由图可见调制模块产生的谐波失真和量化失真处在相同的水平上，不能被明显区分开来，模块的THD+N达到-90 dB。

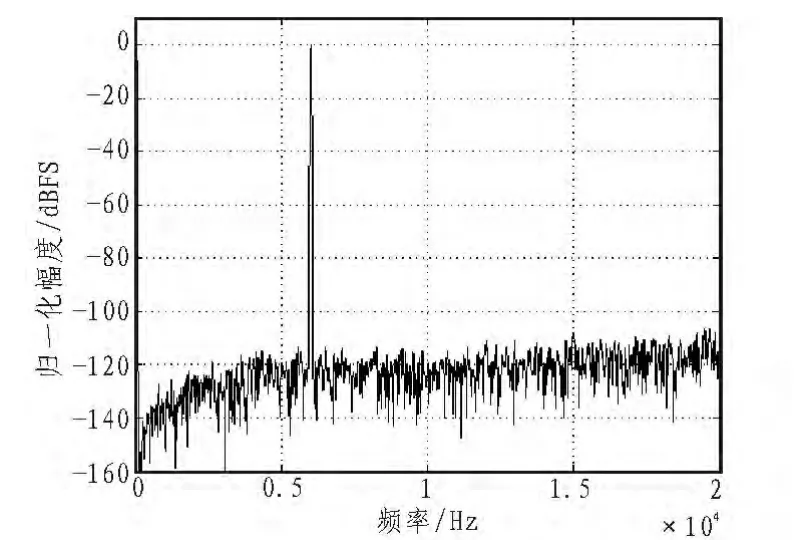
图4 调制模块输出频谱仿真结果Fig.4 Spectrum of modulator’s simulation result

3.2 调制模块的硬件实现

本文构建的双边PWM调制立体声音频数字D类放大器调制模块，使用Altera公司的Cyclone IV E（EP4CE30F23C6N）器件配合前端数字同轴接收模块和后端低通滤波器模块实现。前端模块主要包含数字同轴接口以及解码芯片（CS8416），解码后的数据使用I2S串行音频接口送至FPGA，FPGA在接受到数据后进行音量控制、过采样、调制以及DEPWM调制，将调制过后的PWM信号输出至后端的模拟低通滤波器进行低通滤波器，还原为输入信号。模块主要使用Verilog语言编写，使用FPGA内部的DSP硬核作为乘法器的实现资源，FPGA的通用I/O口作为串行音频输入口和PWM信号的输出口。

该调制模块能够处理48 kHz采样率的24位立体声信号。调制模块中音量控制能够对输入数据的大小进行调节，并能够实现防止输入饱和的作用。过采样部分实现了16倍过采样，采用了4级半带FIR滤波器的结构。调制模块的伪采样部分采用如图3所示的方法实现了双边伪采样。噪声整形部分使用两个5阶调制器来实现，量化精度为5位。PWM发生器部分使用计数器实现，工作于24.576 MHz时钟频率下，输出PWM信号的脉冲重复频率为384 kHz。

伪采样部分中，由于牛顿-拉夫森迭代法涉及到较多的乘法操作，因此使用单个乘法器，按照高频时钟进行分时计算，以降低逻辑资源的消耗。同时将迭代法的计算过程进行化简[6]，减少计算过程中重复的乘法运算，降低逻辑资源的消耗。

3.3 调制模块的性能测试

本文搭建了一个由PC机，数据采集卡以及该调制模块组成的测试系统。使用PC端生成6 kHz的正弦波经由数字同轴输出，经过调制模块之后，使用高速数据采集卡对模拟低通滤波器的输出进行采样，将得到的数据在MATLAB中进行分析，得到模块的性能指标。

图5所示的为对采集卡得到的数据进行频谱分析得到的频谱图。由图可知，调制模块输出的PWM波正确包含了输入的正弦波（6 kHz）信息，达到了调制的目的。但是由于电路的开关瞬态效应、FPGA的通用I/O口的电平转换速度以及模拟低通滤波器的谐波失真等非理想因素，与图4的仿真图比较起来，包含了更多的噪声和谐波失真。由图5可以看出，调制模块引入了2次和3次谐波失真，但其幅度均在-80 dB以下。从图中也可以看出由于量化产生的噪声被调制器推移至20 kHz以上，在音频频带内本底噪声达到了-100 dB左右。调制模块的THD+N在6 kHz达到了-80.5 dB，说明该双边PWM调制模块能够有效的抑制调制中产生的谐波，但是模拟滤波器明显增加了二次和三次谐波，同时本地噪声也有所增加。

图5 模拟低通滤波器输出频谱Fig.5 Spectrum of LPF's output

4 结 论

文中实现了一种用于数字音频D类放大器的双边PWM调制模块，使用牛顿-拉夫森迭代法和多项式拟合法相结合的伪自然采样算法，并通过两个∑Δ调制器进行噪声整形，最终使用PWM发生器产生双边PWM信号。并基于FPGA构建了一个立体声24位数字音频D类放大器调制模块，实现了从数字同轴输入至模拟低通滤波器输出的功能。通过高速数据采集卡采集输出，分析后得到调制模块的THD+N@6 kHz达到-80 dB。证明了该双边PWM调制模块的有效性，但PWM输出端口的高低电平转换特性以及模拟低通滤波器的滤波特性也同样制约着数字D类放大器的性能。

[1]Goldberg J M，Sandler M B.Pseudo-natural pulse width modulation for high accuracy digital-to-analogue conversion[J].Electronics Letters，1991，27（16）:1491-1492.

[2]Pascual C，Song Z，Krein P T，et al.High fidelity PWM inverter for digitalaudio amplification:spectralanalysis,Real-Time DSP implementation,and Results[J].IEEE Trans.Power Electron，2007，18（1）:473-485.

[3]Mellor P H，Leigh S P，Cheetham B G.Reduction of spectral distortion in class Damplifiers by an enhanced pulse width modulation sampling process[J].Circuits,Devices and Systems,IEE Proceedings G，1991，138（4）:441-448.

[4]SONG Zu-kui，SARWATE D V.The frequency spectrum of pulse width modulated signals[J].Signal Processing，2003，83（10）:2227-2258.

[5]Mouton H，Putzeys B.Understanding the PWM nonlinearity:Single-Sided modulation[J]. Power Electronics, IEEE Transactions on，2012，27（4）:2116-2128.

[6]Goldberg J M，SANDLER M B.New high accuracy pulse width modulation based digital-to-analogue convertor/power amplifier[J].Circuits,Devices and Systems，IEE Proceedings，1994，141（4）:315-324.

Double-edge PWM modulator for digital class-D amplifiers

SHI Long-fei， FAN Yang-yu， LV Guo-yun， YUAN Yong-jin， HUANG Bo-hua
（Northwestern Polytechnical University， Xi’an 710129， China）

This paper introduced a double-edge PWM modulator for digital class-D amplifiers，which used pseudo sampling algorithm to reduce the harmonic distortion，the pseudo sampling algorithm is based on Newton-Raphson method and polynomial approximation method.Although many works about single edge PWM modulation scheme have been done recently，but little work are reported on the design of the DEPWM based digital audio amplifier.In this paper we applied a double-edge PWM modulator for digital class-d amplifiers，using well known noise shaping technology and pseudo sampling algorithm.Also， a 24-bits stereo digital class-d amplifier’s modulation module was implemented based on FPGA.After testing， the THD+N@6 kHz of this module has reached-80.5 dB.

digital class-D amplifier； pseudo nature PWM modulation； double edge PWM modulation； Newton-Raphson method；FPGA

TN402

A

1674-6236（2014）15-0112-04

2013-10-27 稿件编号：201310207

陕西省科学技术研究发展计划项目（2012K06-10）；华为公司创新研究计划项目（YJCB2011062RE）

史龙飞（1989—），男，河南新郑人，硕士。研究方向：物理电子学、高速数字信号处理。