摄像机标定中总体最小二乘法抗噪性的研究

邰 晶，翟为刚，谭力宁

（1.第二炮兵工程大学 907教研室，陕西 西安 710025；2.第二炮兵工程大学 701教研室，陕西 西安 710025）

摄像机标定中总体最小二乘法抗噪性的研究

邰 晶1，翟为刚1，谭力宁2

（1.第二炮兵工程大学 907教研室，陕西 西安 710025；2.第二炮兵工程大学 701教研室，陕西 西安 710025）

为了降低摄像机标定中图形加性噪声给标定精度带来的不良影响，提出了基于总体最小二乘法的摄像机标定方法。由于总体最小二乘法具有消除或降低噪声的功能，本文将其用于求解单应性矩阵，既提高了单应性矩阵的精度，又为摄像机内外参数和畸变系数的精确测量提供了理论依据。在此基础上借助OpenCV函数库获取图形中角点高精度坐标的功能，在Visual C++环境下实现了对摄像机的标定。数值实验和实际标定实验均表明，提出的标定方法具有更高的精度和抗噪声能力。

总体最小二乘法；摄像机标定；噪声

摄像机标定是计算机视觉系统中不可缺少的前提和基础，其实质是确定摄像机内外参数的一个过程[1]。基于张氏两步平面模板标定法是目前通常采用的传统摄像机标定方法[2]，该方法过程简单，而且比主动视觉和摄像机自标定方法的精度高，经过多年的研究已经发展的比较成熟。

由于室内条件有限、设备成本较低，数据传输获取摄像机参数的过程中易受电磁信噪的影响，这属于通信系统的内部噪声，因此在采集、获取图像时，均会不同程度地受到干扰，降低图像质量。图像噪声的存在不仅降低了图像的视觉效果，而且对图像获取、边缘检测、特征提取、模式识别等都会带来影响[3]。来自图像传感器的数字图像会受到各种噪声的干扰，其中主要包括加性噪声、乘性噪声和混合噪声，而通信内部的噪声是独立于信号之外的噪声，并以叠加的形式对信号造成干扰，因此加性噪声被看成是通信系统的背景噪声。目前较常用的基于传统最小二乘的两步法，没有抑制图像噪声的有效性能，因而标定结果易受噪声影响。

总体最小二乘法具有抑制输入和输出噪声的能力，因此在很多领域都有着广泛的应用，例如：统计分析、线性和非线性回归、系统辨别、参数估计和信号处理等[4]。本文在考虑加性图像噪声的情况下，设计了基于总体最小二乘抗噪的标定方法，并借助OpenCV实现了对摄像机的标定。数值实验和实际标定实验均表明，基于总体最小二乘法抗噪的标定方法具有更高的精度。

1 相关知识介绍

1.1 标定原理

摄像机通过透镜将空间三维场景成像变换到摄像机二维图像的平面上，即成像变换的描述为摄像机成像的几何模型[5]。摄像机标定的关键是选择合适的成像模型，然后进一步运用成像模型的参数确定摄像机内外部参数。然而实际应用中由于透镜设计因素的影响，采用的摄像机大多都存在镜头畸变，因此，作为定位测量的一部分，必须消除或减小畸变的影响，才能为下一步的精确定位提供理论数值依据。对摄像机内外参数进行的有效标定不仅可以直接提高测量精度，而且可以为后续获取空间物体的尺度、度量信息奠定良好的基础。

在张氏平面标定法中，先采用针孔模型求解摄像机的内外参数，再引入透镜的径向和切向畸变。由于针孔模型很难准确的描述成像几何过程，只有采用校正后的成像模型进行标定才能得到更精确的摄像机参数。在该模型中，空间点在世界坐标系中的坐标值变换为图像平面上像素坐标系中对应点的坐标值的过程可分解为下述的4步变换[6]，如图1。

图1 摄像机标定的原理图Fig.1 Schematic diagram of camera calibration

1.2 单应性矩阵

在计算机视觉中，从一个平面到另一个平面的投影映射定义为平面的单应性。因此平面单应性的一个典型应用就是二维平面上的点映射到摄像机成像仪上的映射。

本文在针孔模型的基础上，采用张氏平面标定法求解摄像机内外参数，并充分考虑到径向畸变和切向畸变带来的影响，求解摄像机的畸变系数[5]。而由针孔成像模型可知，单应性矩阵是求解摄像机内外参数以及畸变系数的前提，它的精度影响摄像机内外参数以及畸变系数的精度，进而影响标定的精度。

如果对三维场景点Q到摄像机二维图像成像仪上的点q的映射使用齐次坐标，则可以用矩阵相乘的方式表示这种映射。

将单应性简单表示为：

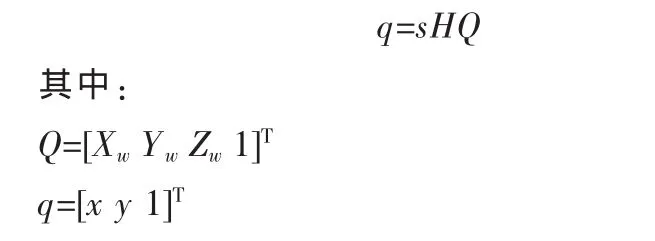
这里引入一个任意尺度比例的参数s。

考虑用平面模板进行标定，特征角点都在同一个平面上，所以令模板平面的Z=0，则单应性矩阵H把三维空间场景模板平面上的点与二维成像仪平面上的点联系起来，表示关系如下：

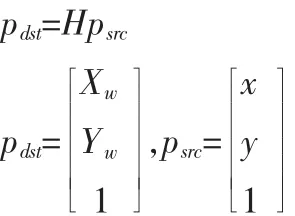
事实上，正是利用同一物体的多幅图像来计算每个视场的单应性矩阵。

1.3 总体最小二乘法

总体最小二乘法的思想很早就被提出来了，它被广泛的应用在统计分析、线性和非线性回归、系统辨别和参数估计以及信号处理中[4]。本文主要针对参数估计提出了总体最小二乘法优化参数的理念，而参数估计中很多问题都归结为求超定方程Ax=y的解。常用的求解方法是最小二乘法，但它只考虑了观测向量y的误差，而在实际问题中观测向量y和数据矩阵A一般都有误差，因此采用总体最小二乘法更为适宜。

总体最小二乘法的数学模型为：（A+E）x=y+e，式中E、e分别为系数矩阵和观测向量的随机误差，具有独立、同分布，服从零均值和方差相同[7]。总体最小二乘的准则为：min[e；E]‖[E；e]‖F，式中，‖‖F表示 Frobenius 范数；[E；e]表示增广矩阵，总体最小二乘法实质就是求解增广矩阵[E；e]的最小范数。

2 基于总体最小二乘法的摄像机标定

在张氏平面标定法中，得到单应性矩阵的方法是采用传统的最小二乘法求解方程组。但这样得到的解通常并不是最优解，而本文的基于总体最小二乘法的摄像机标定，是在考虑图像噪声的基础上[8]，用总体最小二乘法求解单应性矩阵，进一步求出更精确的摄像机内外参数以及畸变系数。

总体最小二乘法摄像机标定的步骤如下方法：

1）三维空间坐标间的变换：世界坐标系中物体点的坐标值 Pw（Xw，Yw，Zw） 和摄像机坐标系中对用点的坐标值 Pc（Xc，Yc，Zc）的转换如下：

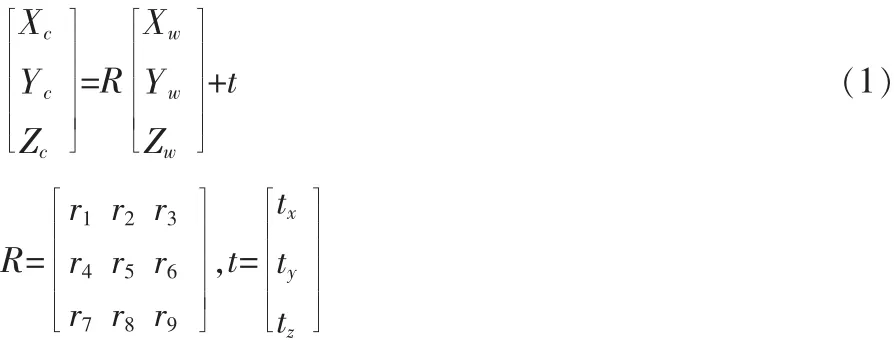
式中：R为一个的旋转矩阵；t为一个平移向量。

2）透视投影：摄像机坐标系中的坐标值 Pc（Xc，Yc，Zc）在针孔模型中透视投影到图像平面上的物理坐标（x，y），得到

其中：f为摄像机成像镜头的焦距。

3）引入透镜畸变后的坐标值 Pd（xd，yd）表示为：

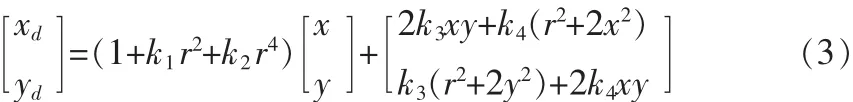
式中：r2=x2+y2；k1、k2为径向畸变系数；k3、k4为切向畸变系数。

4）将图像物理坐标（x，y）转换为图像像素坐标（u，v）：

各参数的意义：假设镜头光轴Z与图像平面的交点为Oi，则原点 Oi在图像像素坐标系下的坐标为（u0，v0），dx、dy 分别为单位像素在x轴与y轴方向上的物理尺寸。

5）摄像机的针孔成像模型：

7）总体最小二乘法求单应性矩阵：

根据n幅图像采集的角点坐标以及对应的世界坐标求单应性矩阵：

由Pdst=Hpsrc得到PsrcTHT=pdstT，一幅图像有m个角点，n幅图像的单应性表示为：

当mm≥9时式（7）有解，而总体最小二乘法的数学模型为：

①基于奇异值分解的总体最小二乘法。将增广矩阵[A；y]进行SVD得：

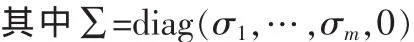
②总体最小二乘估计为：

3 基于OpenCV的摄像机标定的实现

OpenCV（Open Source Computer Vision Library）是一个开源的计算机视觉库，最初由Intel公司发起并开发[9]。它包含许多图像处理和计算机视觉常用的算法，有效提高了开发效率，已经广泛应用于对实时性要求较高的计算机视觉的系统开发。

为了实现摄像机的标定，调用 OpenCV函数库，它有采集图像和角点提取的功能，可以从不同的角度抓取几张平面标定模板的图片，获取高精度的图像坐标[10]。具体标定过程如下：

1）粗精度角点提取

读取一组标定用的图像数据，使用cvFind Chessboard Corners函数提取角点进行筛选图像。读入一组图像数据，当该幅图像上设定的角点数目和提取的相同，表示角点提取成功，该图像存储到文本文件中；否则，表示提取角点失败，返回该幅图像要放弃，则继续标定，直到可用的标定图的数目满足设定的最少标定用的图的数目。

2）亚像素级角点细化提取

当提取到了所需要角点的图像像素坐标值后，为了得到更为精确的角点位置，我们需要对这些角点做进一步的细化，使用函数cvFindCornerSubPix进一步精确得到角点位置的坐标；使用函数cvDrawChessboardCorners将检测到的角点在图像中显示出来。

3）计算内外参数

将角点在世界坐标系中的坐标值以及对应的图像坐标系中的坐标值代入式（6）中，结合式（7）（8）（9）（10）总体最小二乘法的求解原理，得到单应性矩阵。依据传统两步法的标定方法以及总体最小二乘法得到的单应性矩阵，求解摄像机内外参数以及畸变系数。

4）误差分析

根据标定得到的摄像机各内外参数，计算已知的角点三维坐标在图像上的投影坐标，即使用了重新投影的方法来计算定标误差，将其与通过角点提取得到的投影坐标进行比较，从而得到一个误差。

4 实验结果与分析

4.1 检验TLS的抗噪性

利用数值实验一次测量的数据，分别使用总体最小二乘法和传统标定的两步法进行摄像机的标定。单应性矩阵的精度直接影响后边标定摄像机内外参数以及畸变系数的精度。一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。本文中使用信噪比（Signal-to-Noise Ratio，SNR）描述噪声水平，SNR 的单位为dB，定义如下：

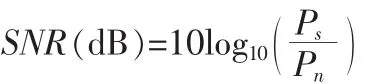
PsPn在考虑通信系统图像噪声为背景的情况下，加入10dB的白噪声得到如表1所示数据。

为了更直观的比较，本文采用误差百分比来描述总体最小二乘法和最小二乘法的性能优势，定义如下：

其中，无噪声为标准值，LS、TLS为测量值。

上述实验数据和图表显示，总体最小二乘法比传统最小二乘法的图像抗噪有明显的优势，这样得到的单应性矩阵的精度有所改进，更接近实际理论值。依据摄像机标定的原理，进而精确标定摄像机的内外参数以及畸变系数。

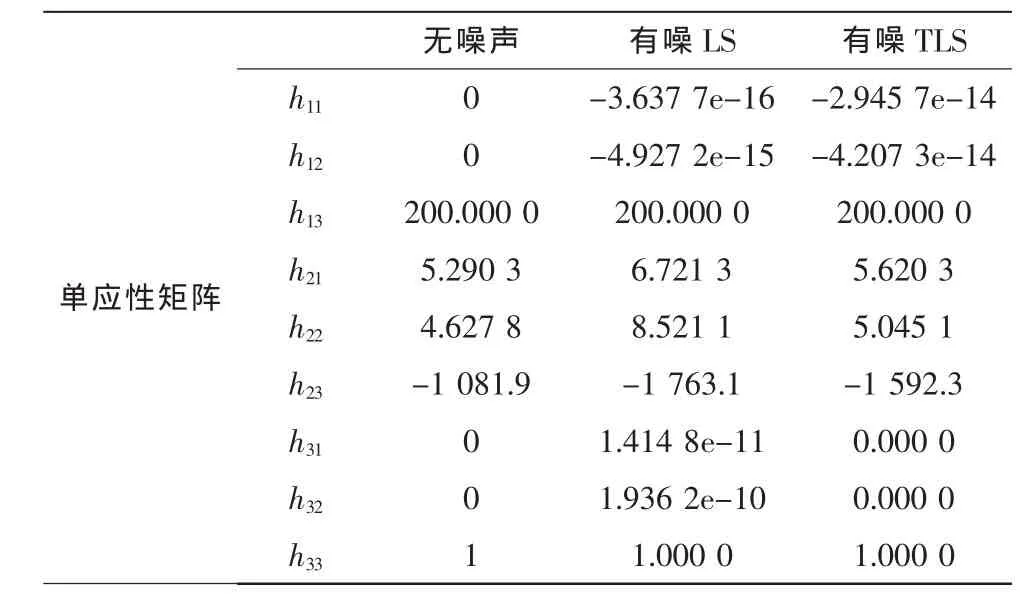
表1 单应性矩阵数值Tab.1 Homography matrix numerical

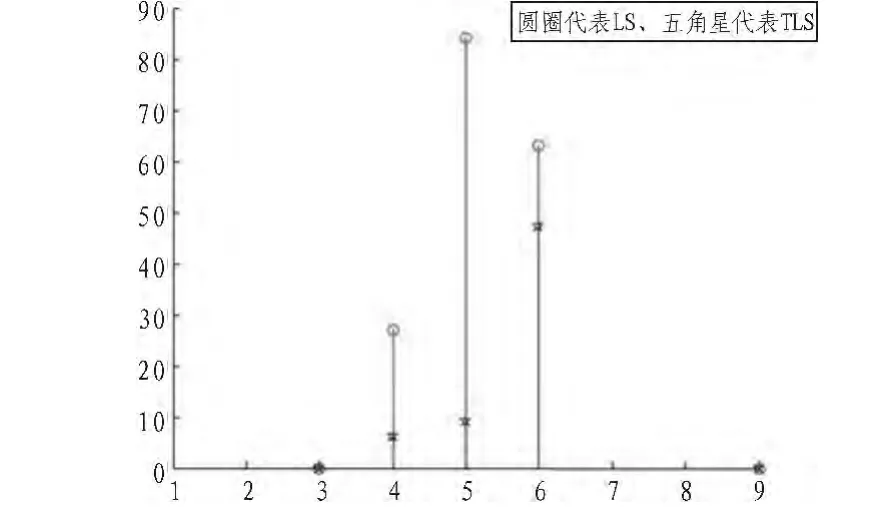
图2 误差百分比Fig.2 Percentage error

4.2 摄像机标定

本文的测量系统是应用在室内环境中，摄像机位置固定不变，测量前要先进行摄像机标定。基于上述标定算法的编写程序，对系统采用蓝色妖姬S8摄像头，在Visual C++的平台上，利用OpenCV摄像机标定的原理，进行基于总体最小二乘法的摄像机标定。标定过程中采用如图3所示的平面棋盘格作为标定的模板，从不同位置和角度拍摄模板图像，检测出棋盘格图像上的所有角点，即可标定出摄像机的内外参数以及畸变系数。

图3 平面棋盘格标定模板Fig.3 Planar checkerboard calibration template

标定过程中成功提取标定角点，如图4所示。

依据上述的标定原理，得到的结果如下表所示：

摄像机的内参矩阵如表2所示。

摄像机的外参矩阵如表3所示。

在得到摄像机的内外参数后，为了比较总体最小二乘法和最小二乘法标定的准确性和精度，本文采用反解棋盘格角点空间坐标的方法，与实际坐标进行对比。列出坐标比较的结果如表4所示。

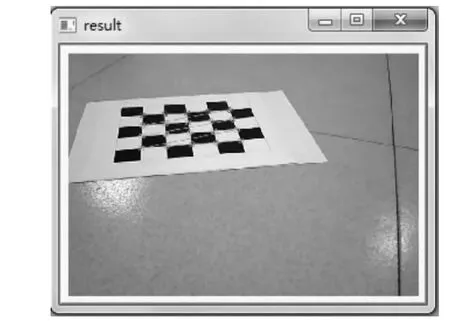
图4 角点提取成功Fig.4 Corner extraction success

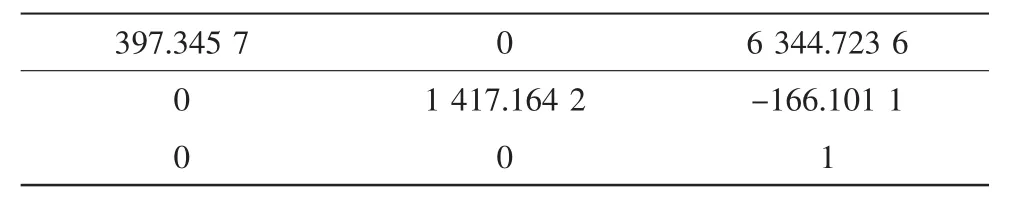
表2 内参矩阵Tab.2 Intrinsic matrix

表3 外参矩阵Tab.3 Extrinsic parameters

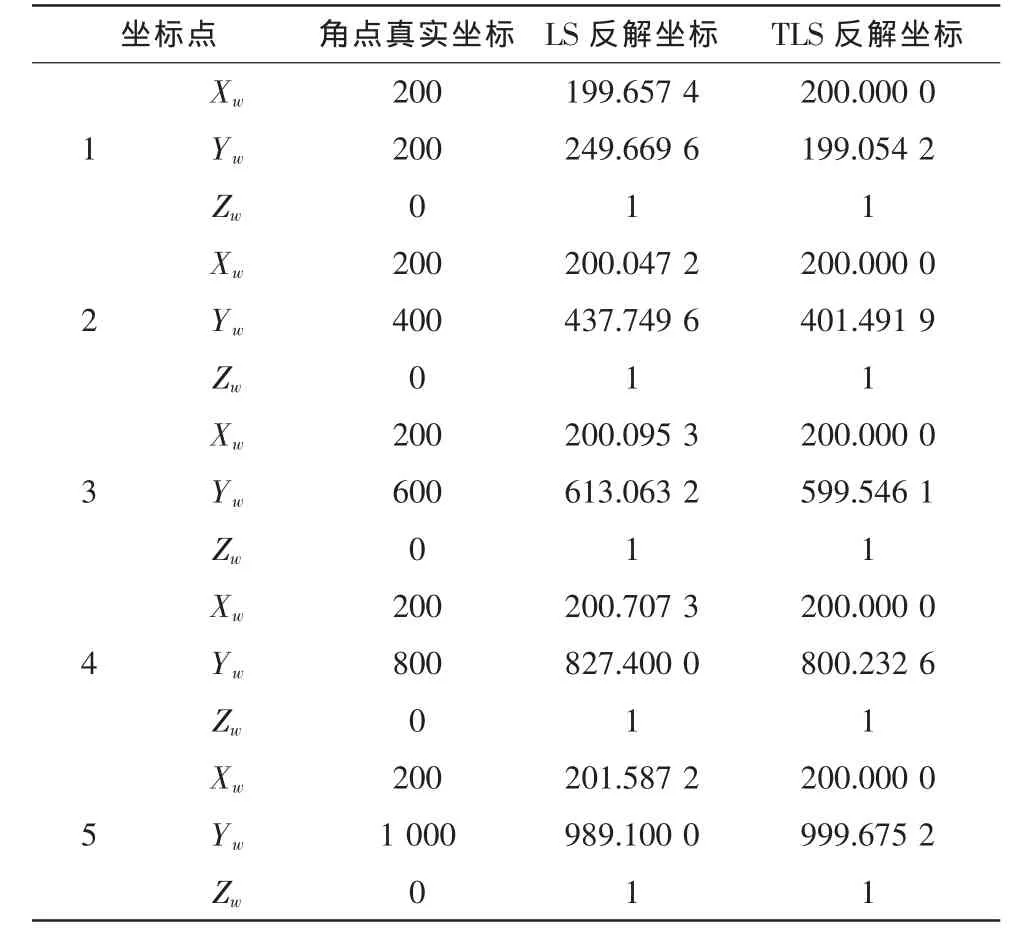
表4 角点实际坐标与反解坐标的比较Tab.4 Comparison of corner actual coordinates and Inverse coordinate

通过上述数据的比较，总体最小二乘法抑制噪声求解的标定参数精度更高，坐标更接近实际值，进一步说明了总体最小二乘法的抗噪性应用在摄像机标定中的可行性价值。

5 结束语

本文对基于OpenCV[11-12]的摄像机标定进行了研究，针对目前标定方法精度易变，通信内部噪声对图像的危害和测量误差影响的缺点，提出了总体最小二乘法抗噪的方法。总体最小二乘法有抑制噪声优化参数的性能，相比传统的最小二乘法更适宜，标定的结果更接近实际数值，而且具有方法简单、标定参数结果精度较高等特性，它可以有效的应用于测量、机器人和其他计算机视觉系统中。

[1]QIU Mao-lin，MA Song-de，LI Yi.Overview of camera calibration for computer vision[J].Acta Automatica Sinica，2006，26（1）:43-55.

[2]Jean-Yves Bouguet.Camera calibration toolbox for Matlab[EB/OL].2004.http：//www.vision.caltech.edu/Bouguetj/calib_doc.

[3]BING Yuan-yuan，WU Wen-bo.Image noise reduction based on wavelet packet and realization with Matlab[J].Journal of Liaoning TechnicalUniversity：NaturalScience Edition，2008，5（27）:224-226.

[4]K H irakawa，T W Parks Image denoising using total least squares[J].IEEE Trans on Image Processing，2006，15 （9）:2730-2742.

[5]WANG Hong-ping，CAO Guo-hua，LI Zhen-hui，et al.Study of Distortion Correction of Image Based on BP Neural Network[J].Journal of Changchun University of Science and Technology：Natural Science Editon，2009，32（4）:653-656.

[6]Zhang Z.A flexible new technique for camera calibration[J].IEEE Transaction on Pattern Analysis and Machine Intelligence，2000，22（11）:1330-1334.

[7]ZHANG Hong-yue，HUANG Jing-dong，FAN Wen-lei.Total lease square method and itsapplication to parameter estimation[J].Acta Automatica Sinica，1995，21（1）40-47.

[8]LI Xuan，SONG Zhan-jie，WANG Yin，et al.Image Denoising based on total least squares[J].Computer Engineering，2010，36（24）:206-207.

[9]LI Jian，CHEN Chang-ming.Improved two-step video camera calibration on the basis of OpenCV[J].Computer Applications and Software，2010，27（3）:104-106.

[10]MAO Jian-fei，ZHOU Xi-yong，ZHU Jing.Improved Twostages Camera Calibration From a Plane[J].Journal of Image and Graphics，2004，9（7）:846-852.

[11]王冬，夏乙，殷木一，等.基于OpenCV的摄像机标定方法实现[J].现代电子技术，2013（8）:97-100.WANG Dong，XIA Yi，YIN Mu-yi，et al.Method of camera calibration based on OpenCV[J].Modern Electronics Technique，2013（8）:97-100.

[12]雷建锋，汪伟.基于OpenCV的图像阈值分割研究与实现[J].现代电子技术，2013（24）:73-76.

LEI Jian-feng，WANG Wei.Research and implementation of image segmentation threshold based on OpenCV[J].Modern Electronics Technique，2013（24）:73-76.

The research on camera calibration of total least squares method for noise immunity

TAI Jing1， ZHAI Wei-gang1， TAN Li-ning2
（1.Faculty 907， The Second Artillery Engineering University， Xi’an 710025， China；2.Faculty 701， The Second Artillery Engineering University， Xi’an 710025， China）

In order to undermine the uncertain effect of image additive noise for the precision of the video camera calibration，a camera calibration method based on the total least squares is proposed.It is used to solve homography matrix because the method can remove or reduce the noise.The method can not only improve the accuracy of homography matrix but also provide the theory basis for the accurate measurement of the camera parameters and the distortion coefficient.With the help of high precision corner point coordinate obtained by OpenCV Library，the video camera can be calibrated by Visual C++.Numerical experiments and practical calibration experiments indicates that the calibration methods based on total least squares has more precision.

the total least squares method；camera calibration；noise

TP391

A

1674-6236（2014）15-0039-05

2013-09-24 稿件编号：201309178

邰 晶（1987—），女，河南新乡人，硕士研究生。研究方向：室内定位。