局部剪切破坏模式下的无重地基承载力

杨 扬，卢坤林，朱大勇

（合肥工业大学 土木与水利工程学院，合肥 230009）

1 引 言

地基极限承载力理论是土力学中的一个经典课题，虽已取得了许多硕果，但绝大多数的理论计算方法是建立在地基整体剪切破坏模式的基础上的，而对局部剪切破坏和冲剪破坏模式下的地基极限承载力理论的研究甚少。Terzaghi[1]采用了降低土体强度参数的方法，并给出了局部剪切模式下的地基承载力经验计算方法；Vesic[2]通过引入土的压缩影响系数修正地基承载力理论公式的方法来计算局部剪切或冲剪模式下的地基极限承载力；吴雄志[3]从极限平衡理论及地基中塑性区发展规律的角度出发，对局部剪切破坏模式下地基极限承载力进行了研究；Lu[4]讨论了砂土地基的冲剪破坏机制，并给出了理论计算方法。

综上所述，目前对局部剪切破坏模式下的地基承载力理论计算方法很不完善，已有代表性成果存在着经验成分偏多、缺乏理论根基的不足。鉴于此，本文将土体强度参数逐渐发挥的概念引入地基承载力中，建立了局部剪切破坏模式下的无重介质地基极限承载力计算方法，并与已有成果进行了比较分析，验证了方法的合理性。

2 地基3种破坏模式的划分

地基极限承载力受到了地基土的强度和变形两方面的制约，从渐进破坏的角度来说，随着荷载的逐渐增大，土体塑性区不断扩散，破裂面不断延伸，同时竖向沉降量也逐渐增大。若地基刚度较大，则土体强度占据主导作用，破裂面贯通并延伸到地面，发生整体剪切破坏；若地基刚度较小，则土体变形占据主要作用，沉降量达到了破坏标准，破裂面并未延伸至地面，此类破坏属于局部剪切破坏或冲剪破坏。

图1给出了3种地基破坏示意图，图中pu、q、γ0和d分别为地基极限承载力、超载、平均重度和基础埋深。当破裂面连续贯穿主动区（I区）、过渡区（II区）和被动区（III区）并延伸至地面，则属于整体剪切破坏（图1(a)）；当破裂面贯穿到被动区，但并未延伸到地面，此类破坏定义为局部剪切破坏（图1(b)）；若破裂面仅延伸到过渡区，地基达到了破坏，则界定为冲剪破坏（图1(c)）。

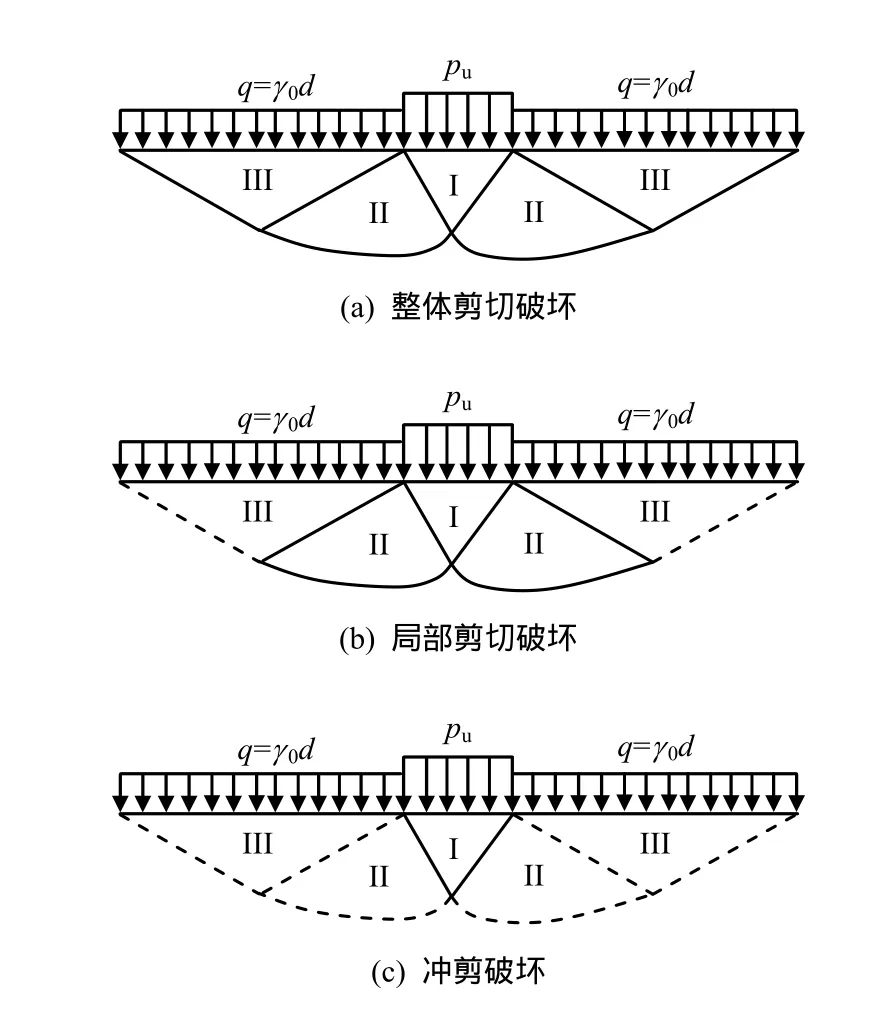
图1 地基3种破坏模式示意图Fig.1 Three kinds of failure modes of foundation

3 局部剪切破坏土体强度的发挥

如图2所示，当地基发生局部剪切破坏，破裂面(EABC)上的土体强度完全发挥出来，潜在破裂面(CD)上的土体抗剪强度并未完全发挥出来，即被动区的被动土压力处于非极限状态。Bang[5]认为，土体从静止状态到极限状态是一个渐变而非突变或跳跃的过程。Fang等[6]的模型试验结果表明，土体从静止土压力向被动土压力演化过程，实际上就是土体抗剪强度逐步发挥的过程。Chang[7]认为，其近似符合线性规律变化。结合上述观点，由地基从渐进破坏的角度可以认为，潜在破裂面上的土体抗剪强度是由被动土压力（C点）逐渐过渡到静止土压力（D点）。本文不妨也假定为变化规律符合线性关系，即C点和D点分别为被动土压力和静止土压力，CD间为非极限被动土压力。

对于无重介质，其具体表达式为

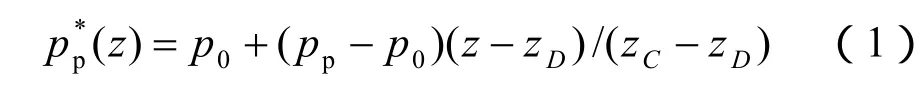
式中：pp*(z)、pp、p0分别为非极限被动土压力、被动土压力和静止土压力；z为计算点的竖向坐标；zC和zD为C点和D点竖向坐标。

图2 局部剪切破坏模式及潜在破坏区土压力Fig.2 Local shear failure mode and earth pressure of potential failure region

4 局部破坏模式下的无重地基承载力

4.1 基本假定

（1）地基土为无重介质；

（2）基底完全光滑；

（3）局部剪切破坏形态仍符合 Prandtl破坏机构；

（4）将两侧埋深土体重简化为两侧地面超载。

4.2 计算模型及受力分析

由于局部剪切破坏破裂面延伸至被动区内，从保守角度可以认为破裂面仅发展至过渡区与被动区的分界处，即图2中的B点。

以图2中的部分滑体FABG为研究对象，其受力情况如图3所示，图中pa、R、r、c和φ分别为主动土压力、反力、过渡区旋转半径、土体黏聚力和内摩擦角，其他符号意义同前。与整体剪切破坏模式相比，二者主要在BG面上的受力情况由被动土压力pp变成非极限被动土压力pp*。

各边界上作用力及几何长度分别如下：

（1）OF边界长度为0.5b，b为基础宽度，荷载为极限承载力pu。

图3 计算模型及受力情况Fig.3 Calculation model and force analysis

（3）FA边界长度为0.5b tan(45° +φ/ 2)，荷载为主动土压力

（4）AB边界黏聚力c沿着边界均匀分布，反力R作用方向指向螺旋线的极点A。

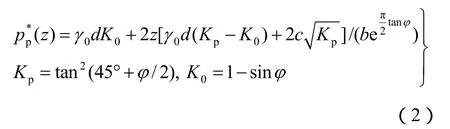
4.3 理论承载力的推求与分析

根据隔离体FABG的静力平衡条件，各边界作用力对极点A取弯矩，应有，则有

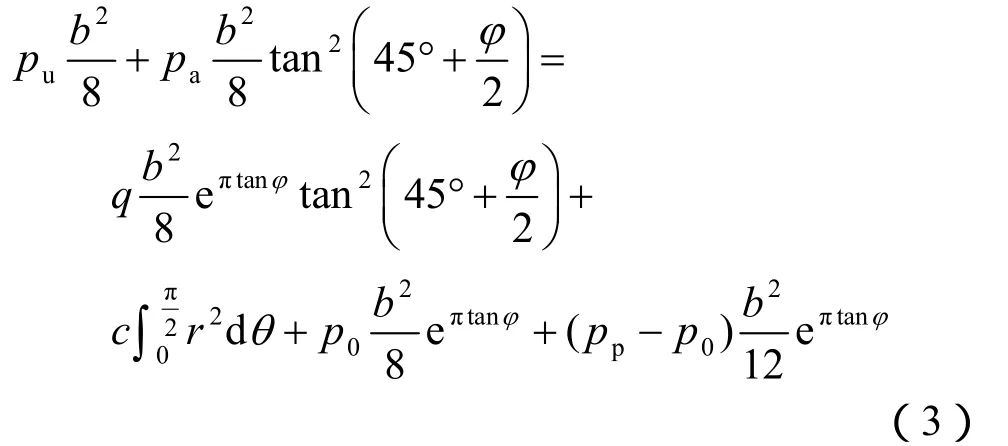
整理得

其中：

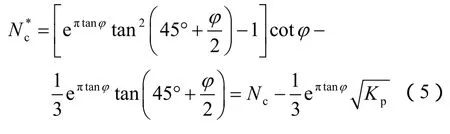
式中：Nc、Nq和分别为整体剪切和局部剪切破坏模式下的承载力系数。比较两种破坏模式下的承载力系数，可以发现：比Nc小比 Nq小

表1为Nc*和Nc以及Nq*和Nq的承载力系数表，可以看出：①局部剪切破坏模式下的承载力系数变化规律与整体剪切破坏模式相一致，均随着内摩擦角的增大而增大；②折减系数ξc、ξq随着内摩擦角的增大逐渐增大，也就是说，内摩擦角越大，Nc*和Nc以及Nq*和Nq之间的差距也越来越大。

表1 整体与局部剪切破坏地基承载力系数表Table 1 Bearing capacity factors of general and local shear failure modes

5 与已有成果比较分析

5.1 代表性成果

对于无重介质而言，局部剪切破坏模式下的地基承载力理论研究代表性的成果主要有Terzaghi的经验公式法[1]和Vesic修正方法[2]，均可统一表示为

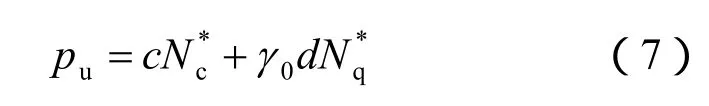
（1）Terzaghi[1]建议，当基底完全光滑时（将对c的折减纳入），分别为

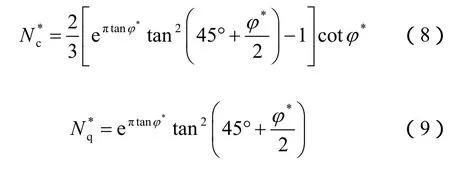
（2）Vesic[2]建议：当地基的刚度指标 Ir＜Ir(cr)时，发生局部剪切或冲剪破坏，此时有

根据Vesic[2]的研究，条形基础的ξc、ξq可表示为

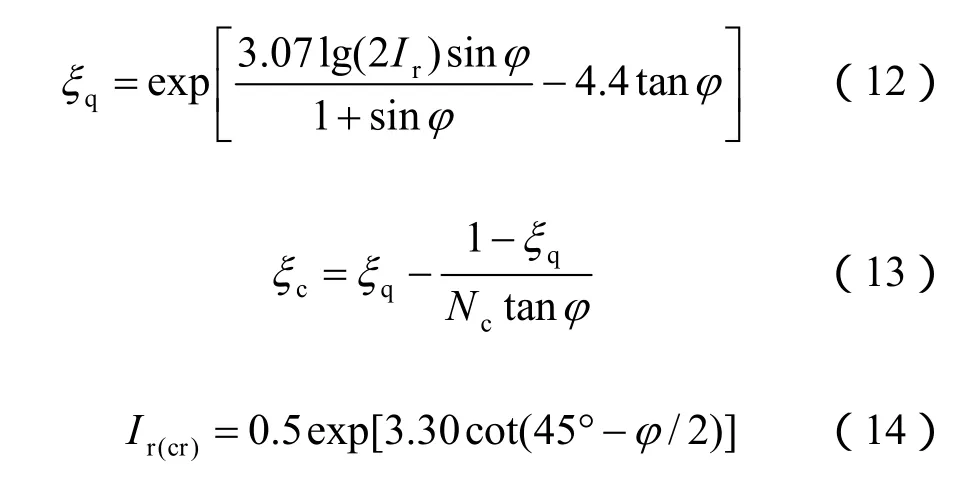
5.2 Nc*和Nq*的比较与评述

当基底完全光滑时，Terzaghi和Vesic的经验公式能够计算局部剪切破坏模式下的无重介质地基承载力，与本文建议公式（式（4））是具有可比性的，因此，通过比较Nc*和Nq*来验证本文方法的可行性。

图4比较了Terzaghi、Vesic和本文方法建议的Nc*和 Nq*，可以得到：①本文方法得到的地基承载力系数Nc*和Nq*随内摩擦角φ的变化规律及趋势与Terzaghi和Vesic经验公式相一致；②Terzaghi经验公式得到的局部剪切承载力偏小，似乎过于保守，文献[8]也得出类似的结论；③Vesic经验方法得到的Nc*和Nq*与Ir/Ir(cr)密切相关，当1.0≤Ir/Ir(cr)时，地基发生整体剪切破坏；当0.5≤Ir/Ir(cr)＜1.0时，该方法计算结果与本文方法比较一致，属于局部剪切破坏模式；若 Ir/Ir(cr)＜0.5，计算结果与本文方法偏差逐渐增大，可以认为地基发生了冲剪破坏。

另外，从理论严密性而言，Terzaghi和 Vesic的计算方法属于经验公式，本文方法则是在一定假设前提下通过严密推导获得的，具有一定的理论基础且计算公式比较简单。

图4 不同方法计算的Nc*和Nq*的比较Fig.4 Comparisons between Nc*and Nq* using different methods

5.3 算例对比分析

有一条形基础，宽为6 m，埋深为3 m，均质地基，土体强度参数c=12 kPa，φ=24°，地基土体的刚度指标Ir=44.58，试确定地基承载力。

首先根据 Vesic理论判断地基的破坏模式，计算得Ir(cr)=80.50，Ir＜Ir(cr)，地基发生局部剪切破坏。

若假定基地为无重介质，不同方法计算结果列于表2中，可以看出，不同方法得到的局部剪切破坏模式下的地基承载力差别较大，本文的上限计算结果与 Vesic方法的计算结果比较接近，下限略低于Vesic方法的计算结果，但高于Terzaghi的计算结果。综上分析，本文方法与前人经典成果基本相一致，验证了本文方法的合理性。

表2 不同方法计算结果的比较Table 2 Comparisons of calculated results using different methods

6 讨 论

6.1 关于3种剪切破坏模式的定义

本文主要依据破坏时地基土中破裂面延伸位置将地基破坏类型划分为3种，与已有划分标准既有联系也有区别。

已有划分标准主要依据 p-s曲线及地表隆起情况，由于3种破坏模式之间的演化是连续而非突变的，对于局部剪切破坏和冲剪破坏的界定就显得比较模糊。若从破裂面延伸位置划分地基破坏类型，就能够比较明确地给出各种破坏模式的界定范围，特别在局部剪切和冲剪破坏模式下地基承载力的理论计算方法研究方面具有优势。

对于局部剪切破坏模式而言，认为破裂面延伸至被动区才能属于局部剪切破坏，与已有划分标准相比，可能会缩小范围。笔者认为，对于工程地基或处理后的工程地基，浅基础地基破坏时破裂面基本上已经延伸至地面或接近地面，也就是说，本文对局部剪切破坏模式的划分，是符合实际工程情况的。另外，这种定义也考虑了计算方便的因素。

6.2 BG面上的土压力分布模式对Nc*和Nq*的影响

图3中BG面上土压力分布模式的不同对局部剪切承载力的大小是有影响的，由于无法得到其真实分布，在假设土压力从被动土压力到静止土压力过渡符合线性规律的前提下，其分布模式也是不确定的，以图5说明，图中J点为被动土压力过渡到静止土压力的分界点，此点位置并未确定，但可以确定的是：当J点与G点重合时，BG面上土压力达到上界；当J点与B点重合时，BG面上土压力达到下界。据此可以确定局部剪切破坏模式下的地基承载力的上界与下界值。

有关上界模式下的局部剪切地基承载力已经在在前文作了分析，结果见式（4）。对于下界模式，采用4.2和4.3节方法和过程，得到局部剪切地基承载力下界解：

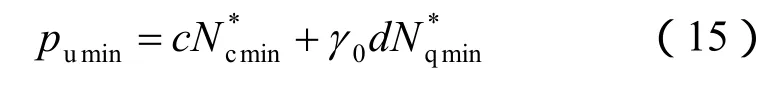
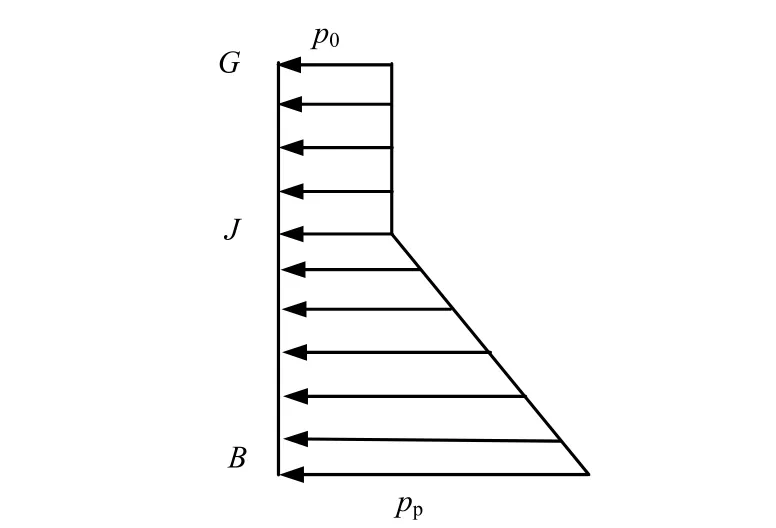
图5 BG面上土压力分布模式示意图Fig.5 Illustration of earth pressure distribution against BG section

其中：

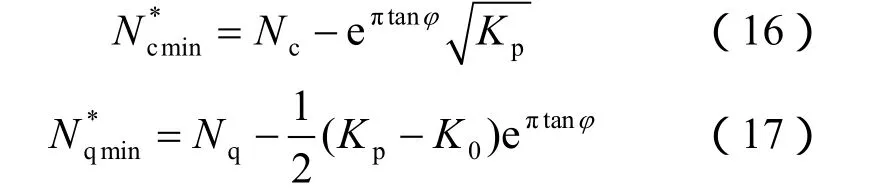
比较式（5）、（6）和式（16）、（17），地基承载力系数Nc*的上、下界之间相差Nq*相差图 6给出了地基承载力系数Nc*和Nq*上界与下界的相对关系，由图可知：承载力系数上、下界限差距随着内摩擦角增大逐渐增大。

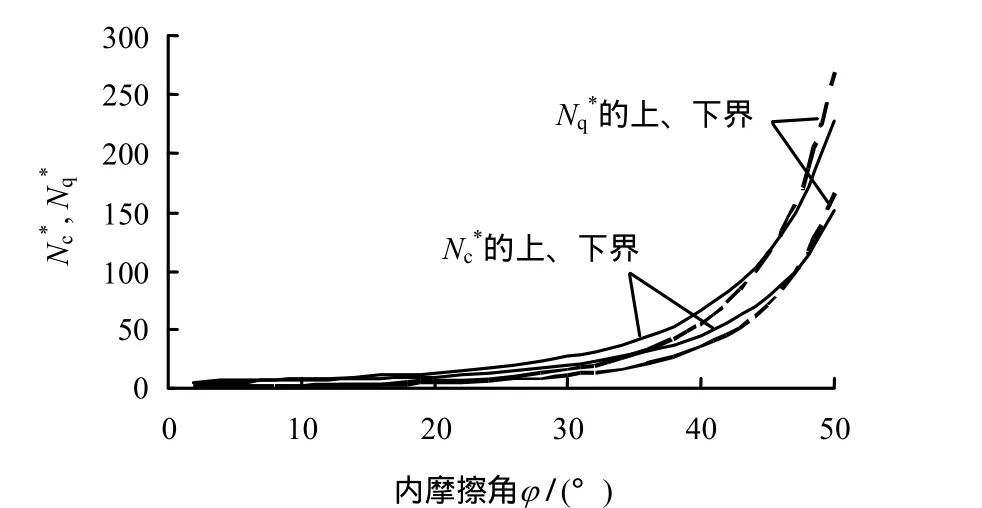
图6 Nc*和Nq*的上、下界值Fig.6 Upper and lower bounds of Nc*and Nq* values

7 结 论

（1）根据破裂面延伸位置，给出了地基3种破坏模式分类的量化标准。

（2）将土体强度参数逐渐发挥的概念引入地基承载力中，建立了局部剪切破坏模式下的无重介质地基极限承载力计算方法。另外，还讨论了土体强度发挥模型对局部剪切破坏承载力系数Nc*和Nq*的影响，给出了取值上、下界限，在实际工程应用中，可根据土体实际情况予以选取。

（3）对于有重介质以及考虑基底粗糙等情况的局部剪切破坏模式下的地基承载力将是下阶段研究的重点。

[1]TERZAGHI K.理论土力学[M]. 徐志英译. 北京: 地质出版社, 1960.

[2]VESIC A S. Bearing capacity of shallow foundations[M]//Foundation Engineering Handbook. New York: Van Nostrand, 1975: 121－147.

[3]吴雄志, 王育德. 局部剪切破坏模式下地基极限承载力的研究[J]. 工业建筑, 2003, 33(2): 41－42.WU Xiong-zhi, WANG Yu-de. Study on the ultimate bearing capacity of ground under local shear failure model[J]. Industrial Construction, 2003, 33(2): 41－42.

[4]LU T K. Punch-through of spudcan foundation in sand overlying clay[D]. Singapore: National University of Singapore, 2007.

[5]BANG S. Active earth pressure behind retaining walls[J].Journal of Geotechnical Engineering, ASCE, 1985,111(3): 407－412.

[6]FANG Y S, CHEN T J, WU B F. Passive earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, ASCE, 1994, 120(8): 1307－1323.

[7]CHANG M F. Lateral earth pressures behind rotating walls[J]. Canadian Geotechnical Journal, 1997, 34(4):498－509.

[8]钱家欢, 殷宗泽. 土工原理与计算[M]. 北京: 中国水利水电出版社, 1996.