岩体裂隙网络渗流变水温影响分析

徐维生 ，周创兵

（1. 武汉大学 水资源与水电工程国家重点实验室，武汉 430072；2. 武汉大学 水利水电学院，武汉 430072；3. 长江科学院 水利部岩土力学与工程重点实验室，武汉 430010）

1 引 言

渗流问题是岩土工程中常见的问题，当岩体裂隙较稀疏，岩块渗透系数非常小时，应采用岩体离散裂隙网络模型。裂隙网络渗流模型是以线性立方定律为基础发展起来的，然而岩体裂隙渗流本构关系并不一定全是线性的[1－2]。以往对于这类渗流本构非线性问题大多按线性简化，当渗流偏离线性渗流较远时按线性简化会带来较大误差[3－5]。

目前，考虑水流温度影响的主要有连续介质（等效连续）[6－12]和裂隙网络介质模型[13－15]。等效连续介质模型主要适合于裂隙分布较密集、集中，表征单元体较小的情况；而裂隙网络介质模型主要适合于渗流由主要的大稀疏裂隙控制的渗流[16]。

关于裂隙变水温流动，目前对于单裂隙内变水温影响大都将裂隙内水温按平均温度处理，这样单裂隙内水头分布为直线，也即裂隙水流与水力坡降成线性关系。然而裂隙渗流本构关系与水流温度相关，单裂隙变水温渗流裂隙水头分布为曲线，也即裂隙变温水流与水力坡降成非线性关系[2]。本文从水温对裂隙水流渗透系数影响出发，以水流黏滞系数与温度关系试验的经验公式为基础建立模型，推导相关公式，分析变水温对单裂隙及裂隙网络渗流的影响。

2 单裂隙变温水流渗流场分析

2.1 立方定律

对于不考虑水流温度场变化的单裂隙水流，水流满足立方定律：

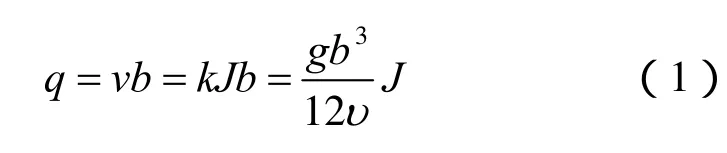
式中：q为单宽流量(m3/(s·m))；v为渗流速度(m/s)；b为裂隙宽度(m)；k为渗透系数(m/s)；υ为运动黏滞系数（m2/s）；J为水力坡降。

2.2 单裂隙变水温水流渗流场分析

2.2.1 单裂隙变水温水流渗流场近似解析解

考虑水流温度场变化的裂隙水流，可以得出水流在裂隙有限小长度内也满足立方定律：

式中：qfin、vfin、bfin、Kfin、Jfin、υfin分别为有限小长度内裂隙单宽流量(m3/(s·m))、裂隙流速(m/s)、裂隙隙宽(m)、裂隙渗透系数(m/s)、裂隙水力坡降、裂隙水流运动黏滞系数（m2/s）。

根据立方定律可知，裂隙渗透系数与水流运动黏滞系数成反比，而水流运动黏滞系数又是温度的函数[1]。目前，广泛采用以下经验公式：

式中：t为水温（℃）。

（1）单裂隙线性变水温分布规律

水流温度在单裂隙内成线性分布，且裂隙两端点温度不相等，则有

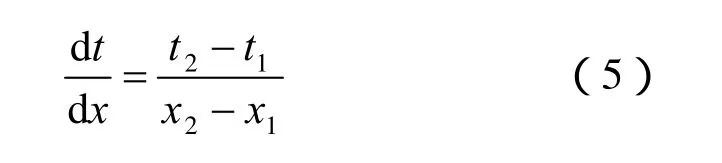
式中：x1、x2为点1、2的坐标值；t1、t2为点1、2的水流温度值；x为长度（m）。

（2）单裂隙线性变水温流量公式

将水头表示成温度场的函数，q为裂隙的单宽流量，裂隙渗透系数k是温度t的函数，运动黏滞系数υ(t)是温度值得函数，即

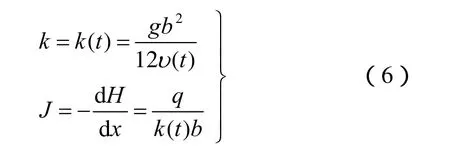
式中：H为水头值(m)。

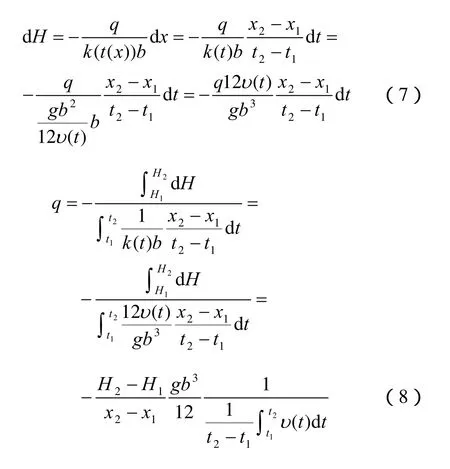
式中：H1、H2为点 1、2的水头值；k(t(x))为渗透系数，是水流温度t的函数，t又是坐标x的函数。

令单裂隙变温水流等效运动黏滞系数为υv，计算公式为

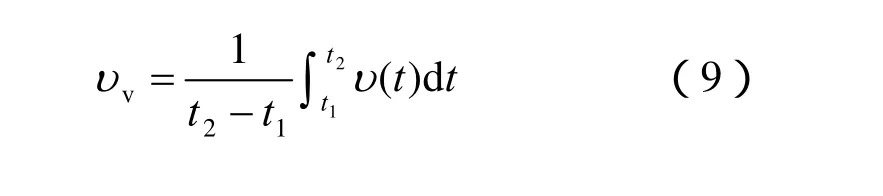
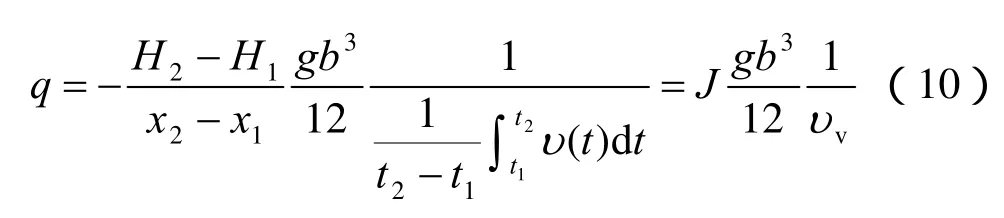
求流量的关键在于求式（11）中积分项，查积分公式可得

对应积分公式可得，a=0.000 221，b=0.033，c=1，b2＞4ac。

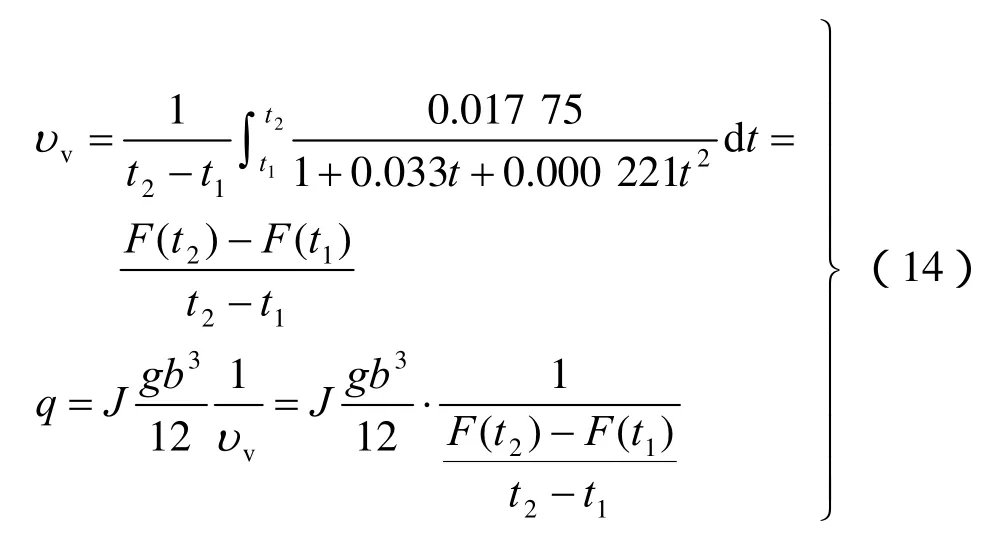
（3）单裂隙线性变水温水流水头公式

裂隙中水温值为t时的水头为H，可推得

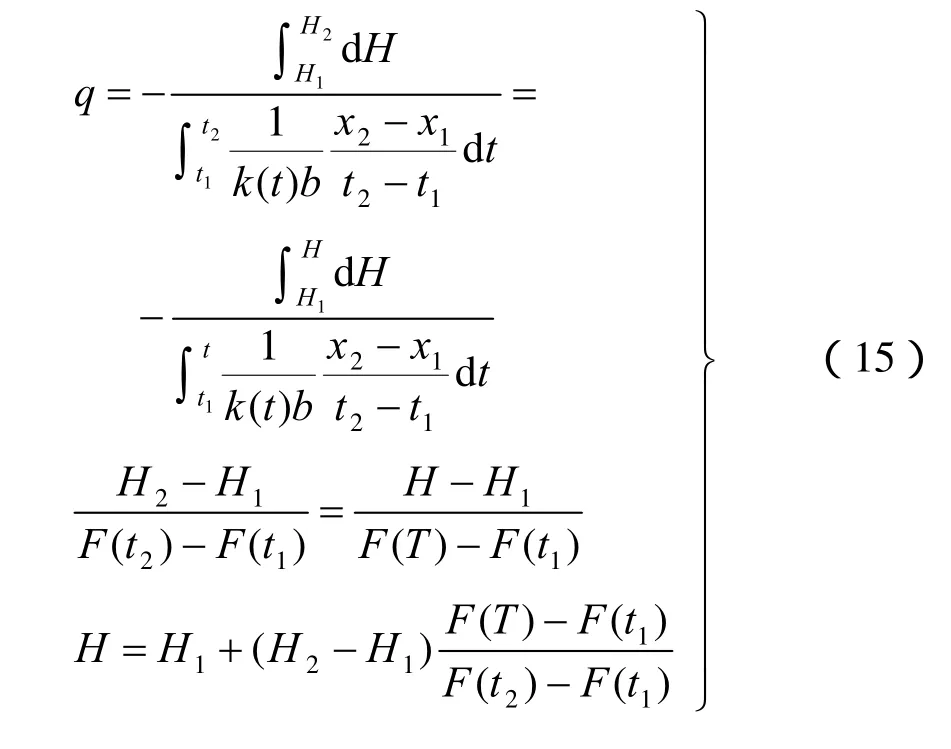
（4）单裂隙线性变水温水流水头分布规律

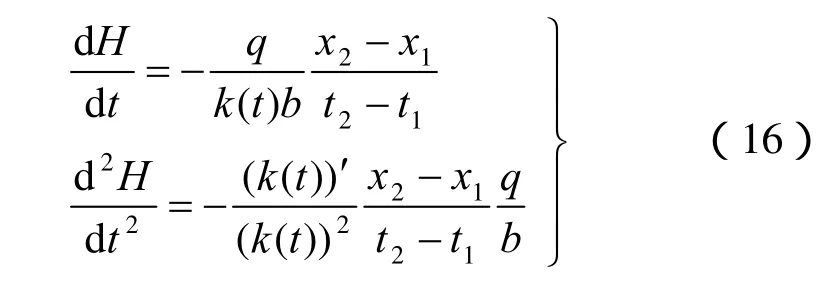
2.2.2 单裂隙变水温水流渗流场分析的有限元解

对于考虑温度场影响的单裂隙线性立方水流，通过第n段的单宽流量为qn，则有

式中：Jn为第n段水力坡降；bn为第n段平均隙宽；υn为裂隙第n段平均运动黏滞系数；Hn-1、Hn分别为第n-1、第n点水头；qn为第n段单宽流量；Δl 为裂隙段长度。

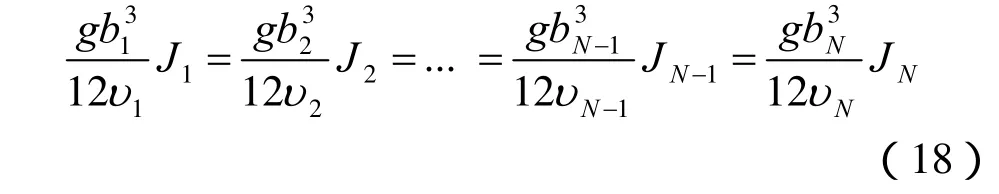
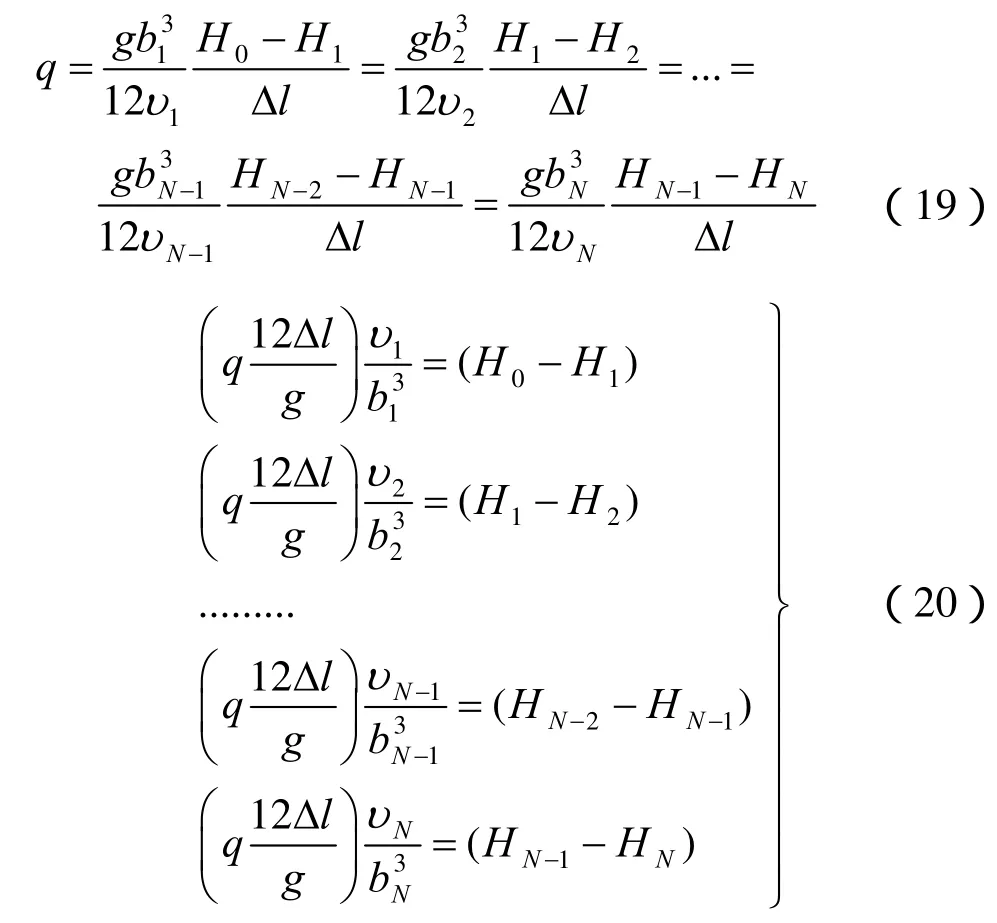
将式（20）中所有等式左右两边相加及将式前n（ n = 1,2,...,N - 1）项等式相加，可得

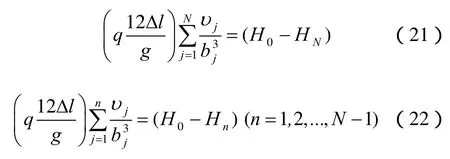
联立式（21）、（22）求解，可得线性立方流第n裂隙段上水头为

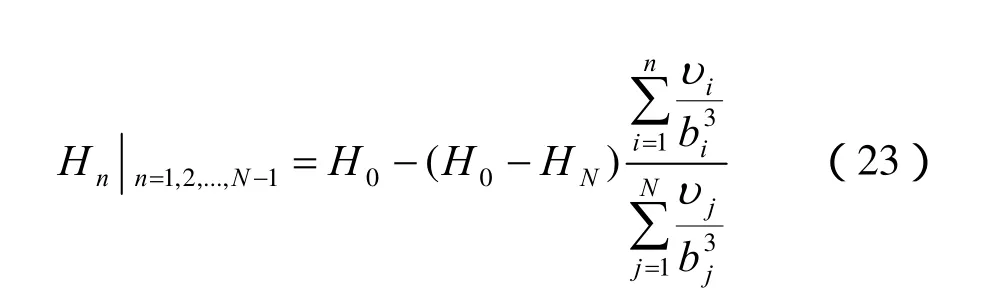
式中：Hn为节点n水头。

求解式（21）裂隙单宽流量q为

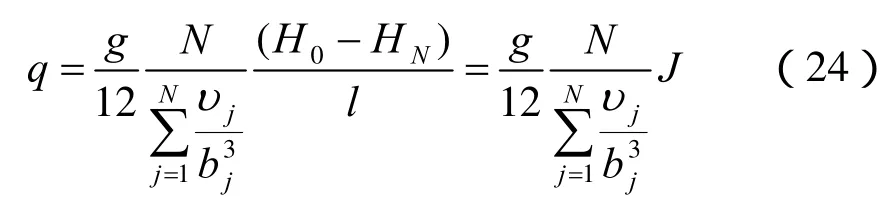
2.3 单裂隙渗流场水温影响分析

以一100 m长单裂隙为研究对象，分工况对裂隙水流进行分析，裂隙示意图见图1。分两种工况，工况表见表1。

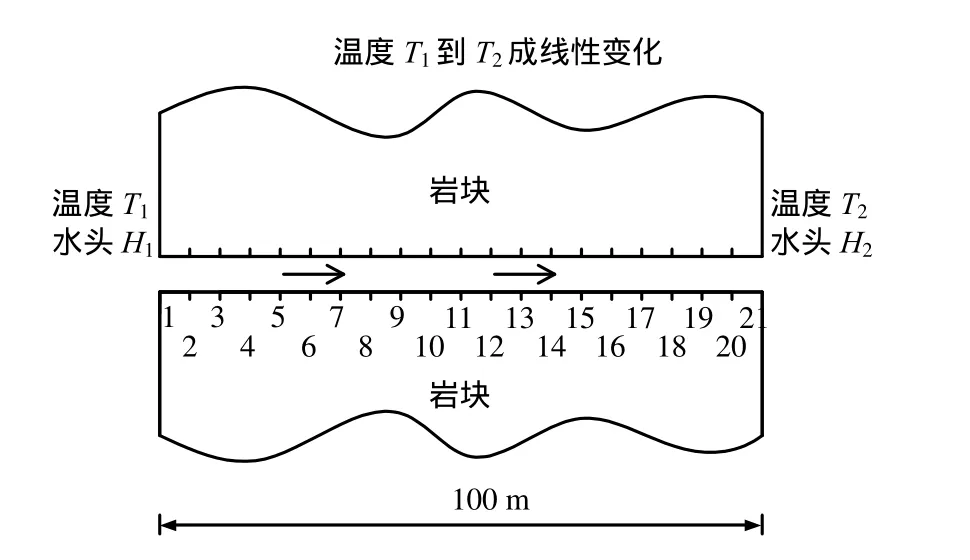
图1 裂隙示意图Fig.1 Sketch map of fracture

表1 计算工况Table 1 Computing conditions

计算结果见表2，由表2结果可得图2。

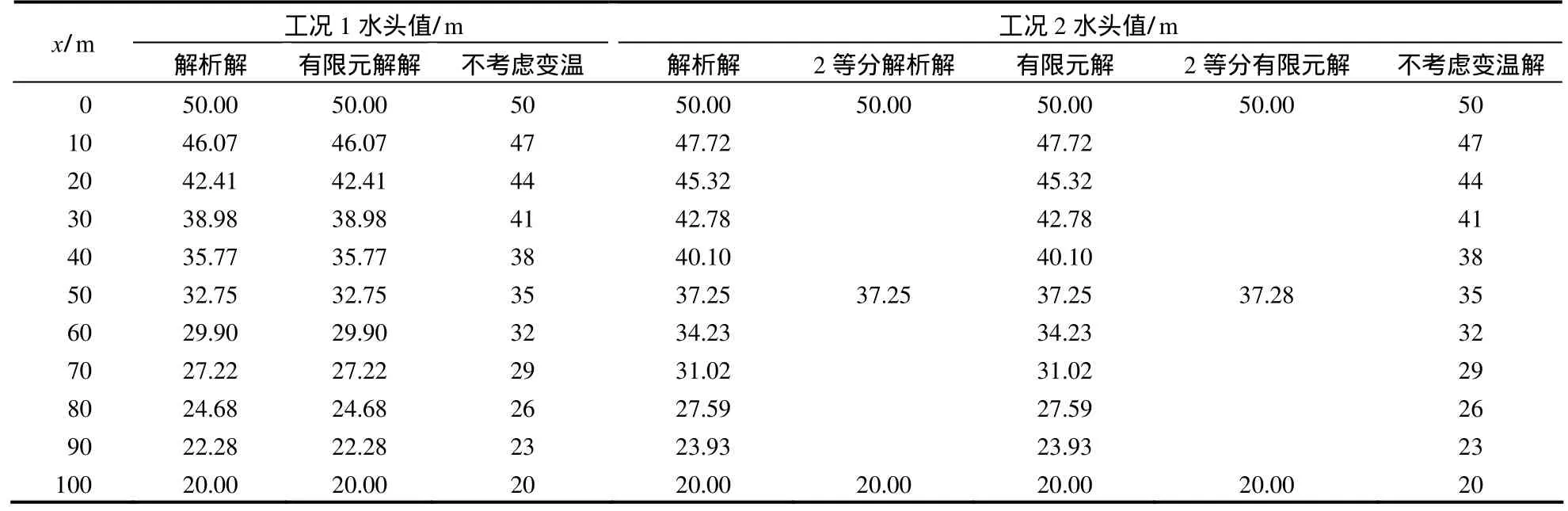
表2 计算结果Table 2 Computed Results

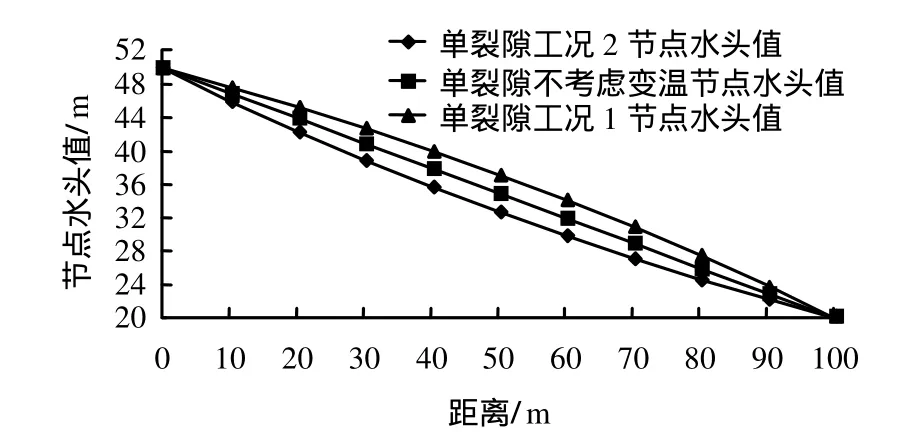
图2 单裂隙变水温水流水头值Fig.2 Water head in single fracture with variable temperature fluid

由表2、图2可以看出：单裂隙内水流由高温流向低温时，水头分布曲线为凸曲线，此时按线性渗流简化渗流水头整体偏小；单裂隙内水流由低温流向高温时，水头分布曲线为凹曲线，此时按线性渗流简化渗流水头整体偏大。当裂隙内节点多到一定程度就非常接近解析解。解析解和子结构解吻合较好，解析解与子结构解结果非常接近，有些节点数值相等，而与不考虑变温作用的水头值相差较大。

3 裂隙网络渗流温度影响子结构法

裂隙内水温不同，裂隙内不同点的水流黏滞系数不同，则水流渗透系数亦不同。因此，当裂隙较长、温度变化较大时，有必要分析裂隙内部水头分布趋势。

（1）裂隙网络变水温渗流近似解析解法

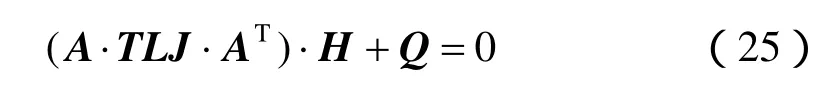
式中：TLJ为水力传导矩阵；T LJ =diag(Tlj1,Tlj2,⋅⋅⋅,T ljm)m×m，A称为裂隙网络的n×m阶衔接矩阵。该矩阵中的元素aij：当j线元不衔接i节点，取0；当j线元衔接i节点，指向离开i节点，取-1，指向i节点取1。

式中：Bj为裂隙网络中第j条裂隙的等效水力隙宽；υvj为第j条裂隙的水流等效运动黏滞系数，裂隙两端点温度不相等时计算方法见式（9），相等时见式（4）。求得裂隙节点水头后，可根据单裂隙渗流近似解析法求解裂隙流量和裂隙内任意一点水头值，具体求法见式（23）、（24）。

（2）裂隙网络变水温渗流子结构法

利用裂隙等效水力隙宽公式和裂隙单宽流量公式先求得裂隙网络中的各裂隙节点水头，再根据式（23）计算每条裂隙段的任一子单元水头和流速。裂隙节点水头公式为

式中：TLD为等效水力传导矩阵；T LD=diag(Tld1,Tld2,⋅ ⋅⋅,T ldm)m×m，且有

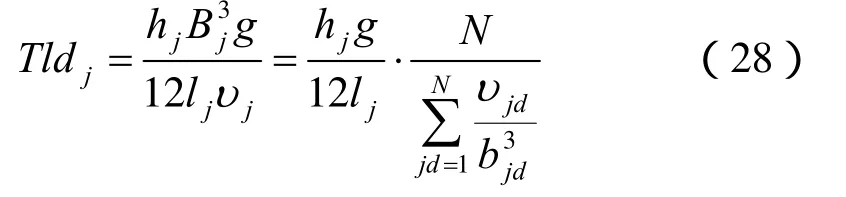
式中：bjd为裂隙网络中第 j条裂隙第d段（子单元）的平均隙宽；υjd为裂隙网络中第j条裂隙第d段（子单元）的平均运动黏滞系数。

求得裂隙的节点水头之后，根据式（23）、（24）分别计算裂隙的等分点（子单元端点）水头和单宽流量，然后求裂隙子单元流速。

4 二维岩体裂隙网络变温渗流分析

选择一200 m×200 m研究区域，区域内有5条裂隙见图3，分别为裂隙BH（裂隙1），裂隙HE（裂隙2），裂隙HF（裂隙3），裂隙HD（裂隙4），裂隙HG（裂隙5），AC、EF为定水头边界，CE、AF为零流量边界。裂隙2的10等分长度为L。

图3 简单裂隙网络Fig.3 Simple fracture network

分7种工况进行渗流计算，具体见表3。

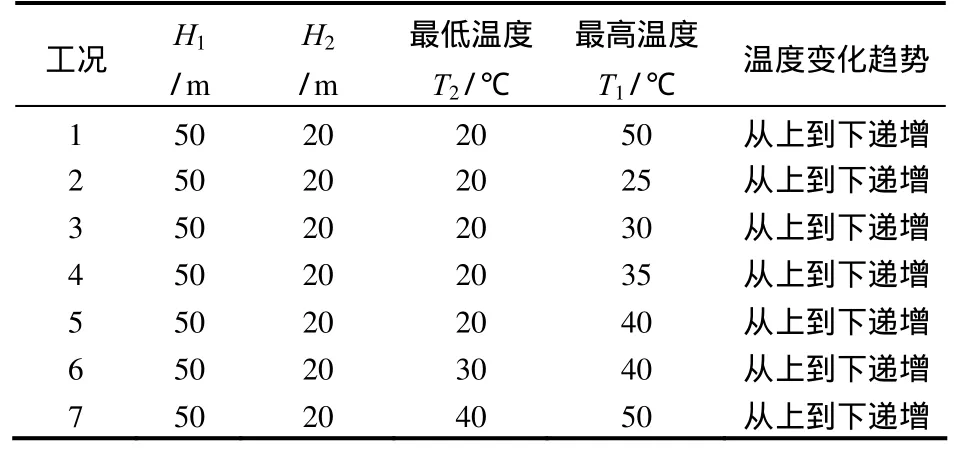
表3 工况表Table 3 Conditions table

表4为工况1、2条件下裂隙2、3内的水头分布值。

表4 工况1、2 裂隙2、3内水头分布Table 4 Water head distribution in fracture No. 1 and No. 2 in condition No. 1 and No. 2

从表4、图4和图5计算的工况1、2条件下的裂隙2、3的水头分布可以看出：单裂隙内，高水温地方水力坡降小，低水温地方水力坡降大。对于裂隙2，水从下往上流，是高温流向低温，裂隙2的水头分布曲线为凸曲线；对于裂隙 3，水从上往下流，是低温流向高温，裂隙3的水头分布曲线为凹曲线。裂隙水流整体温度值越高，裂隙各节点整体水头值越大。验证了文中前部分解析解是合理的。

表5为各工况下裂隙2、3流量值。由表可以看出，裂隙存在偏流效应，即节点水流有偏向水流温度高的区域流动的趋势；温度梯度越大，流量相差越大，水头值相差越大；反之温度梯度越小，则流量相差越小，水头值相差越小。

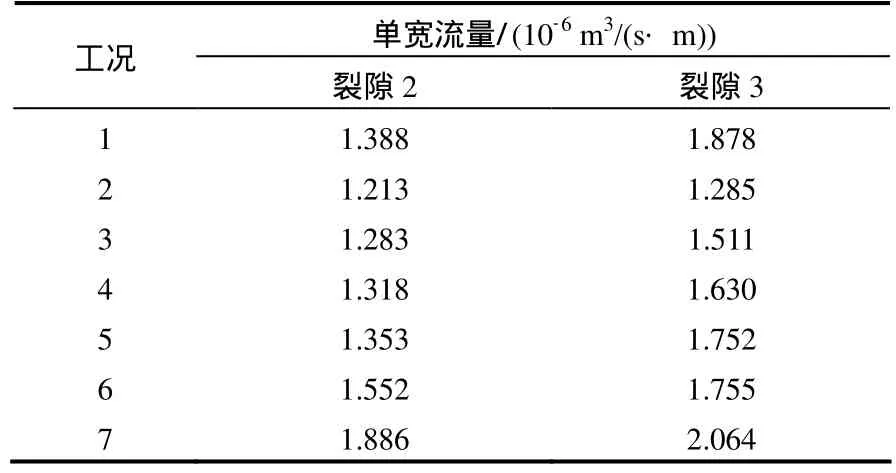
表5 各工况裂隙2、3流量表Table 5 Flows of fracture No.2 and No.3 under various conditions

5 结 论

（1）单裂隙变水温水流内水流水头与水力坡降成非线性关系，当水流由高温向低温流动时，水头分布曲线为凸曲线，此时按线性渗流简化渗流水头值整体偏小；当由低温向高温流动时，水头分布曲线为凹曲线，此时按线性渗流简化渗流水头值整体偏大。

（2）单裂隙内，高水温处水力坡降小，低水温处水力坡降大；裂隙网络内裂隙平均水温越高，流速越快；裂隙网络内存在与裂隙宽度相似的温度偏流效应，即节点水流有偏向水流温度高的流动趋势；温度梯度越大，流量、水头值相差越大；反之温度梯度越小，则流量、水头值相差越小。

[1]柴军瑞, 徐维生. 大坝工程渗流非线性问题[M]. 北京:中国水利水电出版社, 2010.

[2]徐维生. 高坝工程渗流力学中的几类非线性问题研究[博士学位论文D]. 西安: 西安理工大学, 2011.

[3]徐维生, 柴军瑞, 陈兴周, 等. 岩体裂隙网络非线性非立方渗流研究与应用[J]. 岩土力学, 2009, 30(增刊 1):53－57.XU Wei-sheng, CHAI Jun-rui, CHEN Xing-zhou, et al.Study of nonlinear non-cubic seepage in fracture network of rock mass and its application[J]. Rock and Soil Mechanics, 2009, 30(Supp. 1): 53－57.

[4]徐维生, 柴军瑞, 陈兴周, 等. 岩体粗糙裂隙网络渗流分析的子单元法[J]. 水动力学研究与进展(A辑), 2010,25(2): 175－182.XU Wei-sheng, CHAI Jun-rui, CHEN Xing-zhou, et al.The sub-element method on the analysis for the seepage in the coarse fractures network of rock mass[J]Chinese Journal of Hydrodynamics (Seris A), 2010, 25(2): 175－182.

[5]徐维生, 柴军瑞, 陈兴周. 含自由面岩体裂隙网络非线性渗流分析的传导矩阵调整法[J]. 水动力学研究与进展(A辑), 2010, 25(4): 484－482.XU Wei-sheng, CHAI Jun-rui, CHEN Xing-zhou. The conductivity matrix reforming method about non-linear seepage with free surface in fracture network of rock mass[J]. Chinese Journal of Hydrodynamics (Seris A),2010, 25(4): 484－492.

[6]杨更社, 周春华, 田应国. 寒区软岩隧道的水热耦合数值模拟与分析[J]. 岩土力学, 2006, 26(8): 2258－1262.YANG Geng-she, ZHOU Chun-hua, TIAN Ying-guo.Numerical simulation and analysis of moisture-heat coupling for soft rock tunnel in cold regions[J]. Rock and Soil Mechanics, 2006, 26(8): 2258－1262.

[7]张学富, 喻文兵, 刘志强. 寒区隧道渗流场和温度场耦合问题的三维非线性分析[J]. 岩土工程学报, 2006,28(9): 1095－1100.ZHANG Xue-fu, YU Wen-bing, LIU Zhi-qiang.Three-dimensional nonlinear analysis for coupled problem of seepage field and temperature field of cold regions tunnels[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9): 1095－1100.

[8]盛金昌. 多孔介质流-固-热三场全耦合数学模型及数值模拟[J]. 岩石力学与工程学报, 2006, 25(增刊 1):3030－3033.SHENG Jin-chang. Fully coupled thermo-hydromechanical model of saturated porous media and numerical modelling[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Supp.1): 3030－3033.

[9]陈波, 李宁, 糕瑞花. 多孔介质的变形场. 渗流场-温度场耦合有限元分析[J]. 岩石力学与工程学报, 2001,20(4): 467－472.CHEN Bo, LI Ning, GAO Rui-hua. FEM analysis on fully coupled thermo-hydro-mechanic behavior of porous media[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(4): 467－472.

[10]GUO R P. Thermo-hydro-mechanical modelling of the buffer/container experiment[J]. Engineering Geology,2011, 122(3－4): 303－315.

[11]ENGELER I, FRANSSEN H J H, MULLER R, et al. The importance of coupled modelling of variably saturated groundwater flow-heat transport for assessing river-aquifer interactions[J]. Journal of Hydrology, 2011,397(3－4): 295－305.

[12]FREI S, FLECKENSTEIN J H, KOLLET S J, et al.Patterns and dynamics of river-aquifer exchange with variably-saturated flow using a fully-coupled model[J].Journal of Hydrology, 375(3－4): 383－393.

[13]王如宾, 柴军瑞. 非连续裂隙岩体渗流场与温度场耦合分析[J]. 工程勘察, 2006, (6): 18－21.WANG Ru-bin, CHAI Jun-rui. Analysis of coupling seepage field and temperature field in discrete fracture rock mass[J]. Journal of Geotechnical Investigation &Surveying, 2006, (6): 18－21.

[14]ZHANG Y J, YANG C S. Coupled thermo-hydromechanical-migratory model for dual-porosity medium and numerical analysis[J]. Journal of Central South University of Technology, 2011, 18(4): 1256－1262.

[15]ZHANG Y J, ZHANG W Q. 3D thermo-hydromechanical-migratory coupling model and FEM analyses for dual-porosity medium[J]. Science China—Technological Sciences, 2010, 53(8): 2172－2182.

[16]仵彦卿. 岩土水力学[M]. 北京: 科学出版社, 2009: 6－7.