三阶一位量化CIFB结构∑-ΔADC调制器设计

李 新，王 龙，李 俊，黄 璜

（沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870）

三阶一位量化CIFB结构∑-ΔADC调制器设计

李 新，王 龙，李 俊，黄 璜

（沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870）

提出了一种基于Maltab SIMULINK的Sigma-Delta调制器的设计与仿真方法，采用单环三阶CIFB结构、一位量化器位数和256倍过采样率，设计中对噪声传输函数的零极点和系统反馈系数进行了优化，缩小了模拟电路的设计难度，提升了系统稳定性。在考虑积分器的有限直流增益、饱和电压、压摆率和增益带宽等非理想因素情况下进行建模，得到了SNDR和ENOB分别为123 dB，20.14 bits，仿真结果表明，该结构可在低量化位数的情况下，得到较高的精度和较好的稳定性，可在高层次上指导调制器晶体管级电路设计。

Sigma-Delta调制器；一阶量化；CIFB；噪声整形

Sigma-Delta ADC以其高分辨率、高性价比和低功耗等优点在音频处理、ISDN、电子测量和数字录像等中低频领域得到了广泛的应用[1]。其利用过采样(Over-sampling)技术、噪声整形技术，将噪声推向高频，可以精确地将模拟信号数字化。Sigma-Delta ADC包括Sigma-Delta调制器以及数字抽取滤波器，其中核心工作是Sigma-Delta调制器的研制。目前设计中广泛采用的是单环二阶多位量化调制器结构和三阶级联调制器结构。前者量化器位数高，容易受到DAC的非线性影响，后者对电路非理想性因素更加敏感，都增加了模拟电路的设计难度。本文综合考虑结构、系数、非理想性等多方面因素，设计了一种具有一位量化噪声比较器的单环三阶CIFB结构调制器，电路结构简单，受非理想因素影响小，通过在Matlab/SIMULINK环境下进行系统建模，得到了调制器设计所需的相关参数。

1 Sigma-Delta调制原理

一阶调制器基本结构如图1所示，它由模拟输入采样、积分器、一位量化噪声比较器和反馈数模转换器构成。X（t）为待转换输入信号，量化噪声用附加误差Q [nTs]表示，Q [nTs]定义为调制器的输出Y [nTs]与积分器的输出之差[2]。

图1 一阶调制器的基本结构Fig. 1 The basic structure of a first-order modulator

根据图1给出的输入输出关系可以用差分方程来表示：

对输出方程进行Z变换的表达式为：

其中X(z)、Y(z)和Q(z)分别是调制器输入、输出和量化噪声的z变换。X(z)的相乘因子为信号传输函数STF。Q(z)的相乘因子为噪声传输函数NTF[3]。观察 STF和 NTF，z=ejw=ej2πf/fs将z域转换到频域得其幅频响应，其中fs为采样频率。

一阶Sigma-Delta调制器信号传输函数频响为1，具有低通滤波器的特性，量化噪声传输函数有高通滤波特性。在输入信号相关区域，噪声很小而信号增益很大，在超越信号带宽的高频区域，噪声增加，有效抑制量化噪声，实现了噪声整形，提高了有效分辨率[4]。

2 调制器非理想模型

理论上单环三阶调制器可以得出较大信噪比，但调制器在实际工作中受到很多非理想因素的影响。设计采用开关电容（SC）Sigma-Delta调制器结构，为更好地估测实际电路所能达到的性能，起到指导晶体管级电路设计的作用，必须考虑到积分器非理想因素对建模的影响，最主要的非理想因素包括：

1）运算放大器直流增益（Finite Gain）

2）饱和电压（Saturation Voltage）

3）运算放大器增益带宽（Gain-Bandwidth）

4）压摆率（Slew-Rate）

通过SIMULINK结构模型来说明各非理想因素的影响。一个理想积分器SIMULINK模型如图2（a）所示，可推出传输函数为：

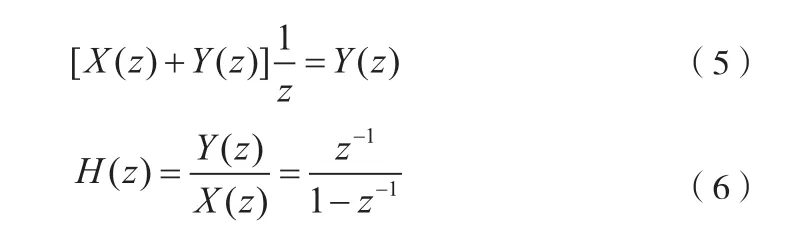
非理想积分器的SIMULINK模型如图2（b）所示，由于积分器电路采用折叠共源共栅结构设计，可以设计出不小于70 dB的直流增益，但仍然非常有限。这就使得直流增益不能全部通过反馈到达输入端，产生了积分器泄露现象。此时的传输函数变为：

有限直流增益为：

图2 积分器模型Fig. 2 Integrator model

运算放大器增益带宽和压摆率通过MATLAB Function引入到非理想积分器中，引起非线性增益，进而对系统产生影响。在SC电路中，有限的增益带宽和压摆率在每个时钟周期内都会输出误差电荷，影响积分器性能。它们对积分器影响可用一个分段函数表示：

其中，alfa为有限增益效应（理想运放为1），Tmax=1/2Ts

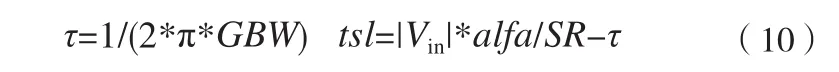
可求得通过MATLAB Function函数的输出为：

3 调制器结构选择及建模

能实现过采样技术和噪声整形技术的调制器结构有很多，常用的调制器结构分为单环和级联两种，其中单环又有一阶、二阶和多阶（包括三阶和三阶以上）结构。虽然一阶和二阶具有结构简单技术成熟等优点，但是在考虑到全差分积分器电路各种非理想因素时，一阶和二阶就很难实现高的动态范围。而三阶调制器可以在和量化器位数为1的情况下实现较大的动态范围、较小的谐波失真和较好的线性稳定性。级联结构是利用绝对稳定的一阶、二阶或稳定的三阶单环调制器结构进行级联实现稳定的高阶调制器。但级联结构需要添加噪声补偿电路，用以抵消前级产生的量化噪声，各级之间系数的偏差会导致噪声泄露，使电路对非理想性因素更加敏感，大幅度添加了模拟电路的设计难度。多位量化器是指采用多位内嵌量化器代替1位内嵌量化器，它的优点是在相同的条件下实现更高的动态范围，增加高阶单环系统的稳定性，但调制器中DAC的非线性限制了调制器性能，需要数字校正或者动态匹配电路来增加DAC的线性度，增加了设计的工作量。常见的单环多阶调制器结构有CIFB、CIFF、CRFB、CRFF。其中CIFB（Cascade-of-integrators, feedback form）结构具有增加调制器稳定性和动态范围的作用，因此选择CIFB结构进行建模。CIFB线性模型如图3，其中反馈回路代表开关电容。

在不考虑各种不理想因素条件下，一个阶数为L、过采样率为M、量化器位数为N的调制器，信号动态范围（DR）和有效位数（ENOB）可以表示为：

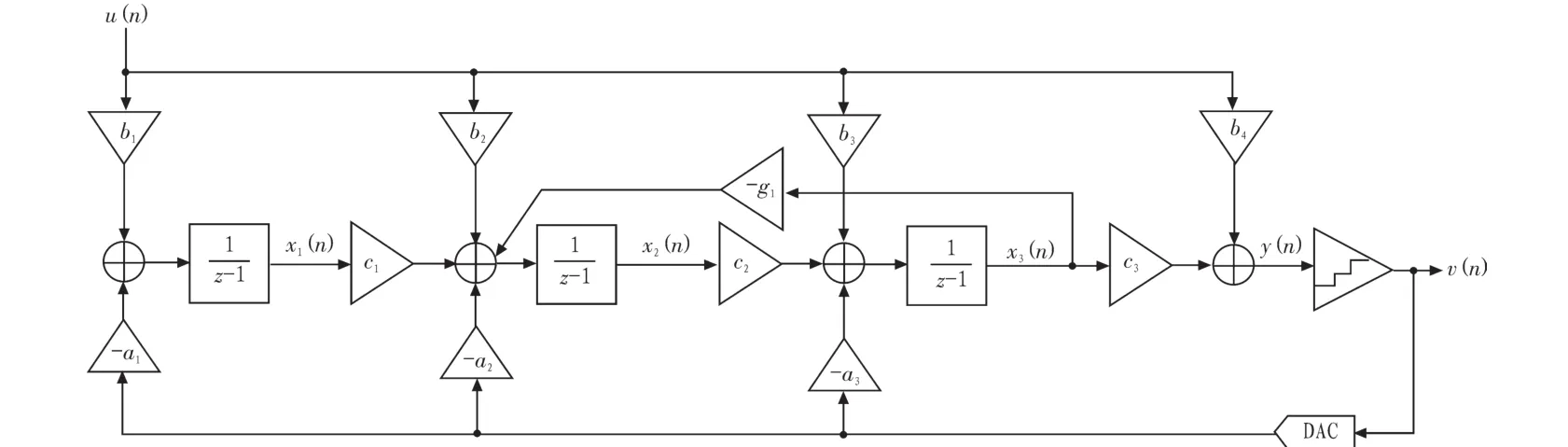
图3 CIFB拓扑结构Fig. 3 CIFB topology

由公式（12）（13）可知，调制器的动态范围与调制器的阶数，过采样率，量化器的位数成正比，当L、N不变时，过采样率M每提高一倍，动态范围提高6.02*（L+0.5）dB，相当于精度提高L+0.5位；当L、M不变时N每增加一位，动态范围提高6.02 dB，精度提高一位。由于实际电路和工艺的限制，调制器的阶数、过采样率和量化器位数不可能无限制的提高。当L=3，M=256，N=1时，通过公式（13）（14）可求得动态范围大于120 dB，有效位数超过20位。

谐振反馈系数g1负责建立在直流附近的两个复数零点，使传输函数的极点保持在单位圆内，用以确保系统的稳定性。一般反馈系数g1的值非常小，对系统的影响并不大，可以忽略不计。为简化分析，令c1=c2=c3=1，根据以上CIFB结构可以推导出环路滤波器的传输函数L0和L1（L0和L1分别是输入信号u(n)和输出信号v(n)到环路滤波器输出信号y(n)的传输函数）的表达式为：

系统的信号传输函数和噪声传输函数和环路滤波器传输函数的关系为：

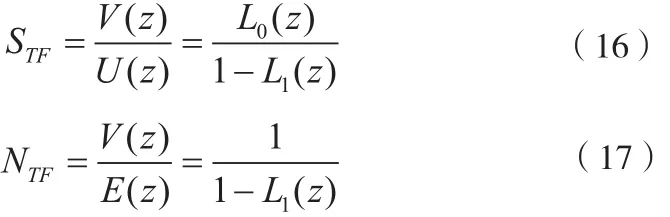
可以推导出信号传输函数为：

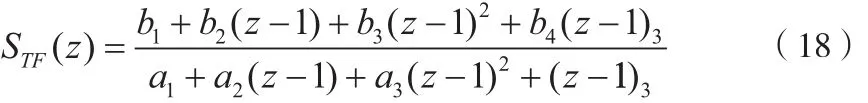
噪声传输函数为：

根据一阶调制器原理，为了保证信号在整个频域内为全通，通常令STF(z)=1。可以推得：

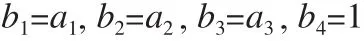
此时噪声传输函数设计就显得尤为重要，选择合适的反馈系数就是选择合适的具有高通特性的噪声传输函数。根据以上分析噪声传输函数的零点都置于直流增益处（z=1）。极点值影响系统反馈系数。为求得系数最优解，采用SDToolbox中的synthesizeNTF函数进行综合[5]，简化了繁琐的计算过程，得到噪声传输函数为：

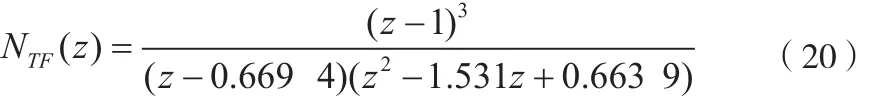
使用Matlab绘制噪声传输函数的零极点分布图以及幅频曲线如4所示。

图4 零极点分布图及幅频曲线Fig. 4 Zero pole distribution figure and amplitude-frequency curve

从图中可知噪声传输函数的零点全部分布在z=1处，极点全部位于单位圆内，证明了系统的稳定性。从幅频曲线上看噪声传输函数为高通滤波特性，信号传输函数为全通，在信号频率以内的噪声能够被大幅度衰减，增加了系统的信噪比。利用realizeNTF函数能够把噪声传输函数的取值映射到积分器的正馈和反馈系数中。最后通过Matlab计算可得：a={0.044,0.288 1,0.799 7};b={0.044,0.288 1,0.799 7,1}; c={1,1,1}; g=0;

但从realizeNTF函数得出的反馈系数并没有经过动态范围扫描，没有明确的输入动态范围，必须确定动态范围值来约束输入信号从而使系统保持稳定。根据“状态-状态”原理，对积分器的输入支路信号以k倍进行缩小，使信号缩减为原值的1/k，再将输出支路系数进行k倍放大，用以防止该级信号衰减对下一级积分器造成干扰。优化系数采用scaleABCD函数确定，对系统输入不同幅度信号，保证系统稳定可得信号输入的最高幅度，以及各级状态。再使用mapABCD函数进行计算，得出优化后的拓扑逻辑结构参数为：

将优化后的反馈系数加入到SIMULINK模型中，可以得到最后的系统模型如图5所示。

图5 三阶单环路系统结构Fig. 5 Three order single loop system structure

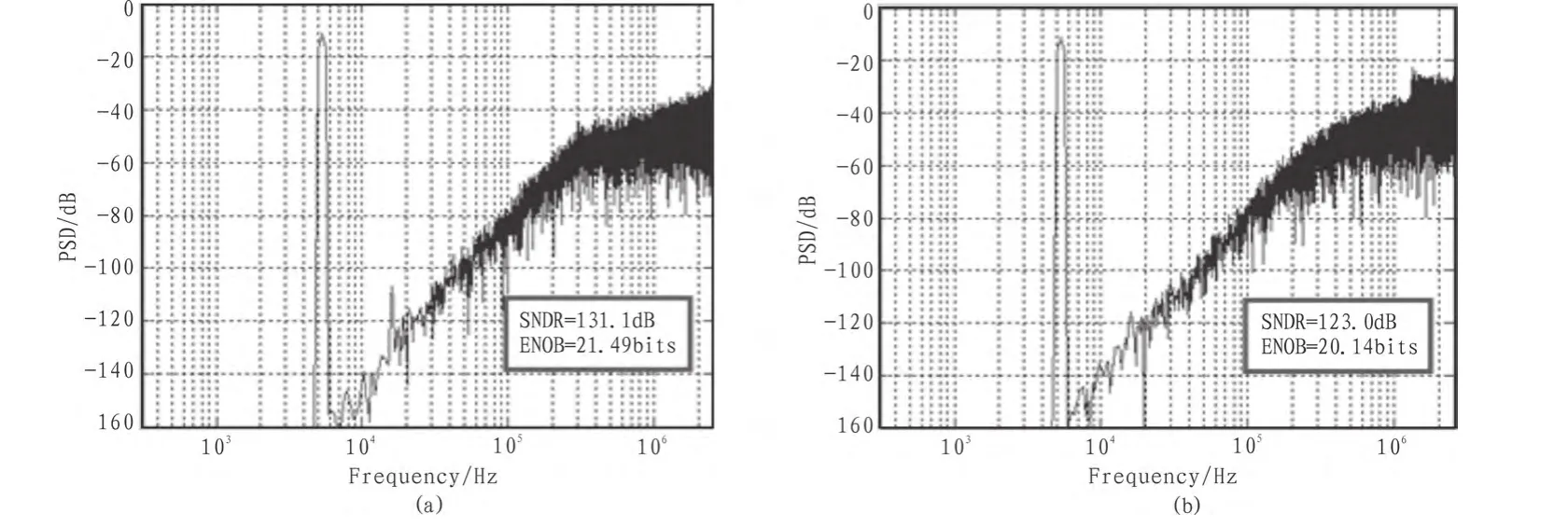
图6 理想和考虑非理想因素时调制器输出频谱Fig. 6 The ideal and non-ideal factors when considering the modulator output spectrum

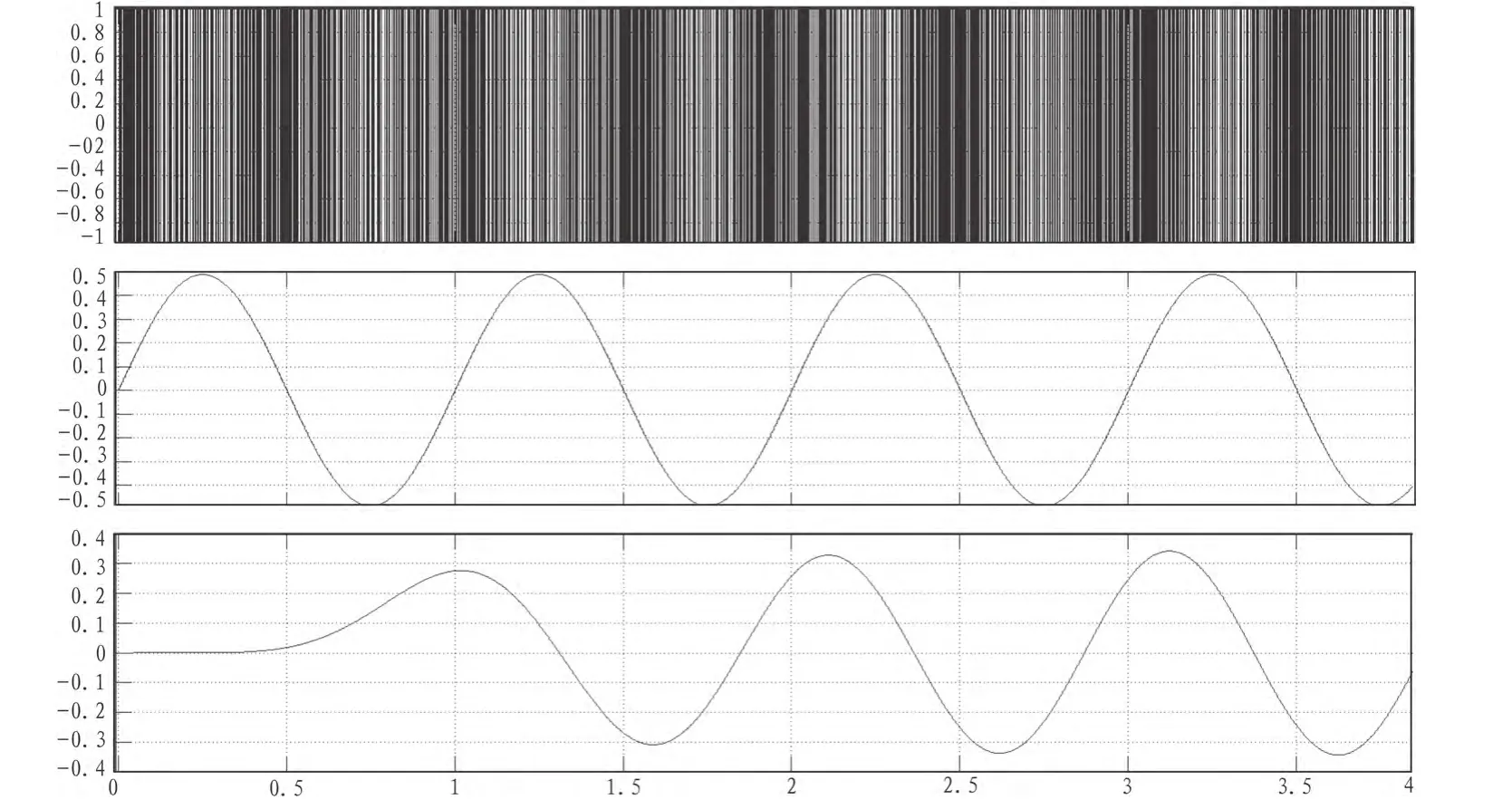
图7 一位量化器输出波形Fig. 7 A quantizer output waveform

图5中的第一级积分器为信号的输入端，信号采样也在第一级完成，因此第一级积分器的性能好坏直接影响到整个调制器的性能[6]。二三级积分器引入的噪声经过噪声整形不会影响系统性能，因此，第一级积分器采用非理想积分器建模。一位量化器采用SDToolbox中ADC-DAC模块。通过更改非理想积分器的各种相关参数，进行大量仿真可以确定调制器的最优参数。仿真时，输入信号幅度为0.5 V，频率为5 312.5 Hz的正弦信号，压摆率为100 V/μs，运算放大器增益带宽为100 MHz，仿真结果如图6所示。

用示波器观察输入输出信号波形如图7所示，最上面为调制器输出PDM码，中间部分为系统输入信号波形，下部分为还原后的输出结果，输出结果与输入信号相比，只是相位发生了变化，并不影响调制结果，这证明了此模型可以正常工作。

4 结束语

基于Matlab设计了具有一位量化噪声比较器的单环三阶CIFB结构∑-△调制器。在考虑各种非理想因素的情况下，采用SDToolbox工具包，进行了仿真验证，结果表明该结构得到了较高的精度，获得了各种性能参数可以用于指导实际电路设计，缩减了芯片设计周期，为其他类似电路设计提供了参考。

[1] Philips K,Nuijten P A C M, Roovers R L J, et al.A continuoustime ΣΔ ADC with increased immunity to interferers[J].Solid-State Circuits,IEEE Journal of,2004,39(12):2170-2178.

[2] Jaykar S,Palsodkar P, Dakhole P.Modeling of Sigma-Delta Modulator Non-Idealities in MATLAB/SIMULINK[C]//Communication Systems and Network Technologies(CSNT),2011 International Conference on.IEEE,2011:525-530.

[3] Chang R G,Chen C Y, Hong J H,et al. Wide dynamic-range sigma-delta modulator with adaptive feed-forward coefficients[J].Circuits,Devices & Systems,IET,2010, 4(2):99-112.

[4] 何乐年,王忆.模拟集成电路设计与仿真[M].北京:科学出版社,2008.

[5] Ranjbar M, Lahiji G R,Oliaei O.A low power third order delta-sigma modulator for digital audio applications[C]//Circuits and Systems,2006.ISCAS 2006.Proceedings.2006 IEEE International Symposium on.IEEE,2006:4762.

[6] Arpaia P,Cennamo F,Daponte P,et al.Modeling and characterization of sigma-delta analog-to-digital converters[J].IEEE Transactions on,Instrumentation and Measurement,2003,52(3):978-983.

Three order a quantitative CIFB Sigma-Delta ADC modulator

LI Xin, WANG Long, LI Jun, HUANG Huang
（ College of Information Science and Engineering, Shenyang University of Technology, Shenyang 110870, China）

Based on Maltab SIMULINK, the design and simulation method of Sigma-Delta modulator with single ring third-order CIFB structure, a quantizer bits and 256 times oversampling rate are investigated. The zero and pole of the noise transfer function and feedback coefficient are optimized to reduce the design difficulty of analog circuit and enhance the system stability. Finite Gain, Saturation Voltages, Slew-Rate, Gain-Bandwidth are analyzed, and the SNDR and ENOB are 123dB and 20.14bits. The simulation results show, in the case of low quantitative figures the structure can get higher precision and better stability. The design parameters can guide the modulator transistor level circuit design at a high level.

Sigma-Delta modulator; a quantitative; CIFB; noise shaping

TN433

A

1674-6236(2014)03-0156-05

2013–06–29 稿件编号：201306206

李 新(1974—)，男，辽宁昌图人，博士，副教授。研究方向：数模混合集成电路。