带有退化效应的多个交货期窗口单机排序问题

方 卓, 罗成新

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

带有退化效应的多个交货期窗口单机排序问题

方 卓, 罗成新

(沈阳师范大学 数学与系统科学学院, 沈阳 110034)

讨论带有退化效应的多个交货期窗口的单机排序问题。其目标函数有2种:第1种是带有提前、延误、交货期的开始位置、交货期的大小及最大完工时间的总费用;第2种是带有提前、延误、交货期的开始位置、交货期的大小和所有工件完工时间之和的总费用。目标是找到多个交货期窗口的最优位置、交货期的大小、属于每个交货期窗口的工件集合和工件的最优排序,使目标函数值最小。将该问题转化为指派问题,并证明其多项式时间可解。

单机; 退化效应; 多个交货期窗口; 提前; 延误; 最大完工时间; 完工时间之和

0 引 言

近年来有关交货期窗口的问题越来越受关注。交货期窗口是指:如果工件在交货期窗口之前完工则产生提前的费用,在窗口之后完工则产生延误的费用,在窗口之内完工则不会有任何费用。Liman[1]等分析了带有待定的公共交货期的单机排序问题。Mor等[2]研究了带有维修活动的交货期单机排序问题,并且每个工件都有一个大小相同的交货期,目标函数是包括提前、延误、交货期的开始时间和交货期大小的总费用。Wang等[3]讨论了带有学习和退化效应的单机排序问题,目标函数包括提前、延误和工期的总费用。Cheng[4,5]等研究了带有退化效应的工期指派问题,目标是确定最优工期及最优的排序使目标函数值最小。文献[6]研究了带有退化效应与维修活动的工期指派问题。文献[7-12]讨论了带有提前、延误的工期指派问题。

本文讨论了2种带有退化效应的多个交货期窗口的单机排序问题。给出了最优解的性质,将2种问题转化为指派问题,并证明其多项式时间可解。

给定m个交货期窗口(1≤m≤n)。di(≥0)和wi(≥di)分别表示第i个交货期窗口的开始时间和结束时间,i=1,2,…,m。Di=wi-di表示第i个交货期窗口的大小。如果m=1,则所有工件有一个共同的交货期窗口,如果m=n,每个工件都有一个交货期窗口。 定义Ii为第i个交货期窗口的工件的集合,当Jj∈Ii时,工件Jj的交货期窗口为[di,wi],i=1,2,…,m。目标是求最优的交货期窗口的开始时间d={d1,…,dm}、交货期窗口大小D={D1,D2,…Dm}、属于每个交货期窗口工件的集合I={I1,I2,…Im}和最优的工件排序,使以下两种目标函数值最小。

问题1 带有提前、延误、交货期开始时间、交货期大小及最大完工时间,目标函数为

问题2 带有提前、延误、交货期的开始时间、交货期的大小及所有工件完工时间之和,目标函数为

1 最优解性质

性质1[13]存在最优排序满足工件的开始加工时间从零时刻开始,且相邻工件之间没有空闲。

2 最优算法

引理1 问题(1)中目标函数可化简为

其中

证明 当m=1时,I={J[1],…,J[n]}

整理可得

其中

同理可得:m=2时,

整理可得

其中

由此可以找出规律,即得到式(3)、式(4)。证毕。

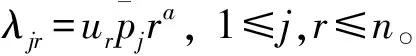
基于上面的分析,给出一个最优算法。

算法1

步骤2 通过式(4)计算λjr。

步骤3 通过解指派问题(5)确定工件的最优排序。

步骤4 计算最优排序的工件的实际加工时间。

步骤5 根据性质3计算最优交货期窗口的位置及交货期的大小。

定理1 对于给定的常数m,如果分配给每个交货期窗口的工件数是确定的,则根据算法1可求出问题(1)的最优解,且算法1的复杂性为O(n3)。

证明 算法1的最优性可由以上讨论所决定。步骤1、2、4和5皆能在线性时间内执行,步骤3转化为指派问题,所以需要O(n3)时间求解,因此算法复杂性为O(n3)。证毕。

引理2 对于给定的m个交货期窗口,分配给每个交货期窗口的工件数是确定的。则问题(2)的目标函数可化简为

其中

证明 与引理1类似。证毕。

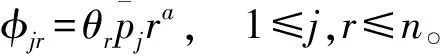
基于上面的分析,给出一个最优算法。

算法2

步骤2 通过(6)式计算φjr。

步骤3 通过解指派问题(7)确定工件的最优排序。

步骤4 计算最优排序的工件的实际加工时间。

步骤5 根据性质3计算最优交货期窗口的位置及交货期的大小。

定理2 对于给定的常数m,如果分配给每个交货期窗口的工件数是确定的,则根据算法2可求出问题(2)的最优解。且算法2的复杂性为O(n3)。

证明 算法2的最优性可由以上讨论所决定。步骤1、2、4和5皆能在线性的时间内执行,步骤3为指派问题,所以需要O(n3)时间内求解,因此问题(2)算法的复杂性为O(n3)。证毕。

3 结 论

本文讨论了2种带有退化效应的多个交货期窗口的单机排序问题。目标是找到多个交货期窗口最优的位置、交货期大小、属于每个交货期窗口的工件集合和工件的最优排序,使目标函数值最小。本文将问题转化为指派问题,给出了最优算法,并证明了在多项式时间内可解。

[ 1 ]LIMAN S D, PANWALKAR S S, THONGMEE S. Common due window size and location determination in a single machine scheduling problem[J]. J Oper Res Soc, 1998,49(9):1007-1010.

[ 2 ]MOR B, MOSHEIOV G. Scheduling a maintenance activity and due-window assignment based on common flow allowance[J]. Int J Prod Econ, 2012,135(1):222-230.

[ 3 ]WANG Jibo , GUO Qian. A due-date assignment problem with learning effect and deteriorating jobs[J]. Appl Math Model, 2010,34(2):309-313.

[ 4 ]CHENG T C E, KANG Liying, Ng C T. Due-date assignment and single machine scheduling with deteriorating jobs[J]. J Oper Res Soc, 2004,55(2):198-203.

[ 5 ]CHENG T C E, KANG Liying, Ng C T. Single machine due-date scheduling of jobs with decreasing start-time dependent processing times[J]. Int T Oper Res, 2005,12(3):355-366.

[ 6 ]YANG S J, YANG D L, CHENG T C E. Single-machine due-window assignment and scheduling with job-dependent aging effects and deteriorating maintenance[J]. Comput Oper Res, 2010,37(8):1510-1514.

[ 7 ]BAKER K R, SCUDDER G D. Sequencing with earliness and tardiness penalties: a review[J]. Oper Res, 1990,38(1):22-36.

[ 8 ]GORDON V S, TARASEVICH A A. A note: Common due date assignment for a single machine scheduling with the rate-modifying activity[J]. Comput Oper Res, 2009,36(2):325-328.

[ 9 ]BISKUP D, JAHNKE H. Common due date assignment for scheduling on a single machine with jointly reducible processing times[J]. Int J Prod Econ, 2001,69(3):317-322.

[10]SHABTAY D, STEINER G. The single-machine earliness-tardiness scheduling problem with due date assignment and resource-dependent processing times[J]. Ann Oper Res, 2008,159(1):25-40.

[11]KUO W H, YANG D L. A note on due-date assignment and single-machine scheduling with deteriorating jobs[J]. J Oper Res Soc, 2008,59(6):857-859.

[12]YANG S J, LEE H T, GUO J Y. Multiple common due dates assignment and scheduling problems with resource allocation and general position-dependent deterioration effect[J]. Int J Adv Manuf Tech, 2013,67(1/2/3/4):181-188.

[13]PANWALKAR S S, SMITH M L, SEIDMANN A. Common due date assignment to minimize total penalty for the one machine scheduling problem[J]. Oper Res, 1982,30(2):391-399.

[14]YANG D L, LAI C J, YANG S J. Scheduling problems with multiple due windows assignment and controllable processing times on a single machine[J]. Int J Prod Econ, 2014,150(4):96-103.

[15]GRAHAM R L, LAWLER E L, LENSTRA J K, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey[J]. Ann Discrete Math, 1979,5(2):287-326.

Multipleduewindowsassignmentandschedulingproblemswithdeteriorationeffectonsinglemachine

FANGZhuo,LUOChengxin

(School of Mathematics and Systems Science, Shenyang Normal University, Shenyang 110034, China)

This paper deals with the single machine multiple due windows assignment and scheduling problems with deterioration effect. We examine two models of the objective function.The first function is to minimize a total penalty function containing earliness, tardiness, due date windows and the makespan costs. The second function is to minimize a total penalty function containing earliness, tardiness, due date windows and total completion time costs. The objective is to determine the optimal due-windows location, due-windows size, the set of jobs assigned to each due window and the optimal sequence of jobs, thus to minimize the total costs. We formulate the problem as a assignment problem and show that the problem remains polynomial time solvable.

single machine; deteriorating effect; multiple due windows; earliness; tardiness; makespan; total completion time

2014-03-17。

国家自然科学基金资助项目(11171050)。

方 卓(1989-),女,辽宁铁岭人,沈阳师范大学硕士研究生;

: 罗成新(1958-),男,辽宁新宾人,沈阳师范大学教授,博士,硕士研究生导师。

1673-5862(2014)04-0471-05

O223

: A

10.3969/ j.issn.1673-5862.2014.04.004