三角高程代替几何水准的可行性
2014-09-22郭旭
郭旭
(深圳市勘察测绘院有限公司,广东深圳 518028)
1 引言
三角高程测量相对于几何水准测量而言,具有作业效率高、操作简单灵活等特点。同时,现在全站仪的测距和测角精度都有很大提高,且精度匹配合理,这使得三角高程测量的精度和可靠性,都有了很大改观。本文依据三角高程测量原理,根据误差传播理论,对三角高程测量精度进行分析和评定,得出在一定条件下,三角高程代替几何水准测量的可能性,使测量工作者可根据实际工作选择最佳水准测量方案。
2 三角高程测量原理及数学模型
2.1 单向三角高程测量及数学模型
实际测量工作中,三角高程测量的距离,通常是几百米甚至上千米。当距离超过 400 m时,地球曲率和大气折光的影响将不能忽视。
三角高程测量时,光线通过密度不均匀的介质时会发生折射,从而使光线成为一条复杂的空间曲线,由此而引起的测量误差,称为气象误差。引起气象误差的代表性原因通常有以下几种:①大气动力的不稳定性;②大气组成的密度梯度;③大气的温度梯度;④大气气压场、风场分布梯度;⑤大气湿度场分布梯度。
三角高程测量原理如图1所示。图1中,S为斜距,α为竖直角,D为水平距离,i为仪器高,v为棱镜高,p为地球曲率对高差的影响(简称球差),r为大气折光对高差的影响(简称气差)。
由图1可得,单向观测的高差计算公式为:
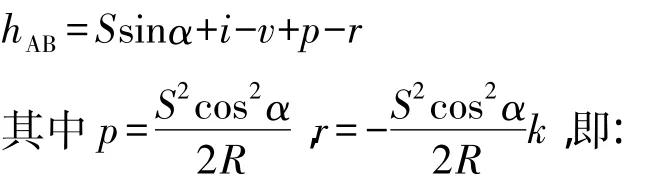
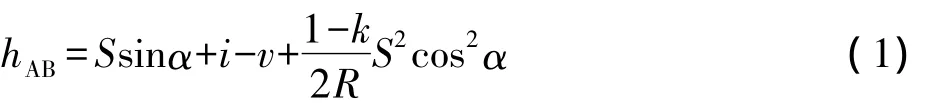
式(1)中,R为地球半径,k为大气折光系数。大气折光系数k与气温、气压,特别是大气密度有关,其值不易测定。
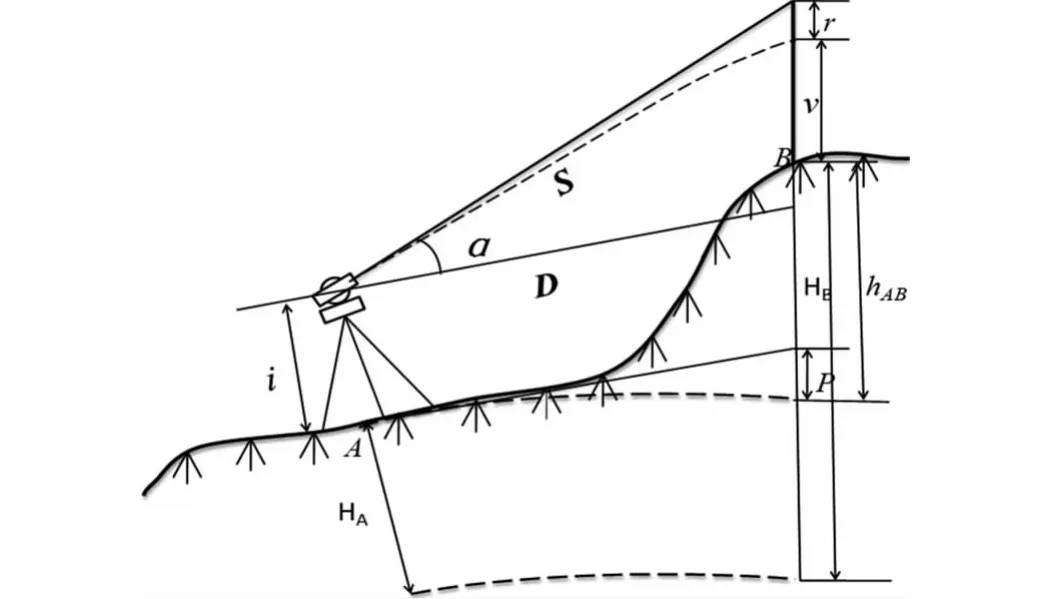
图1 单向三角高程测量
2.2 中间法三角高程测量的原理及数学模型
中间法是将两个棱镜架设在待测高差的高程点上,全站仪架设在距离两点的中间位置,测量原理如图2所示。
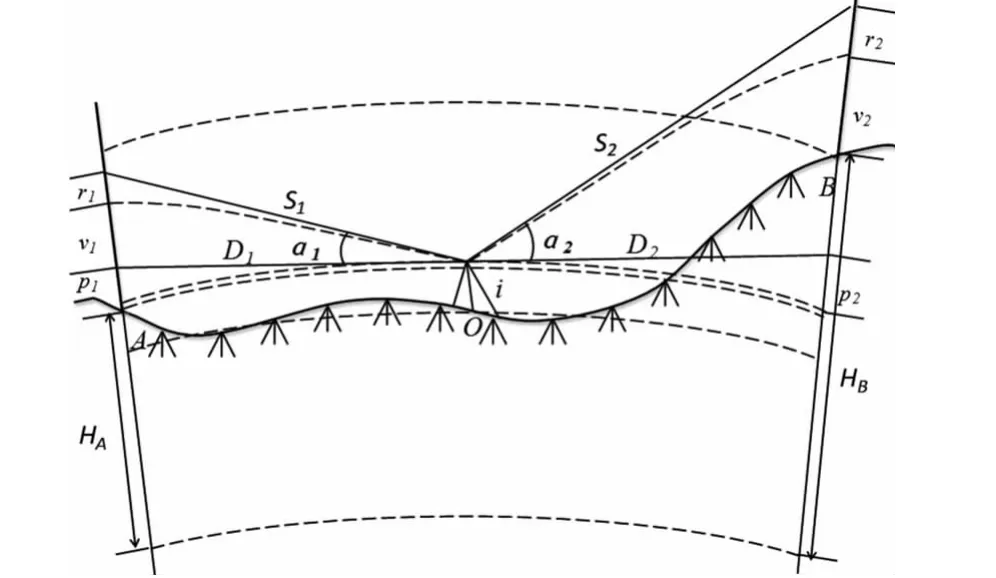
图2 中间设站法三角高程测量
如图2所示,将棱镜分别架设在待测高差的A、B高程点上,在A、B中间,选择与该两点均通视的设站点O,测量过程中无需对中。根据三角高程测量的原理,由式(1)可得,O、A两点的高差hOA为:
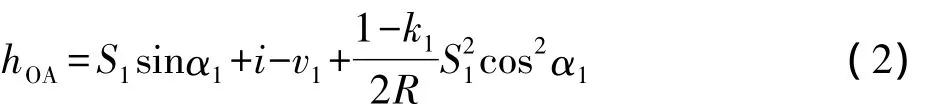
同理可得O、B两点的高差hOB为:
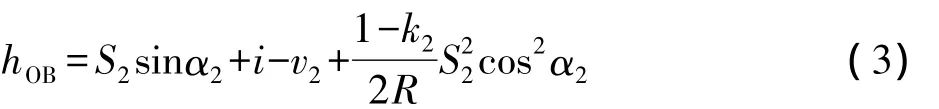
由式(2)、式(3),可得,A、B两点间的高差hAB为:
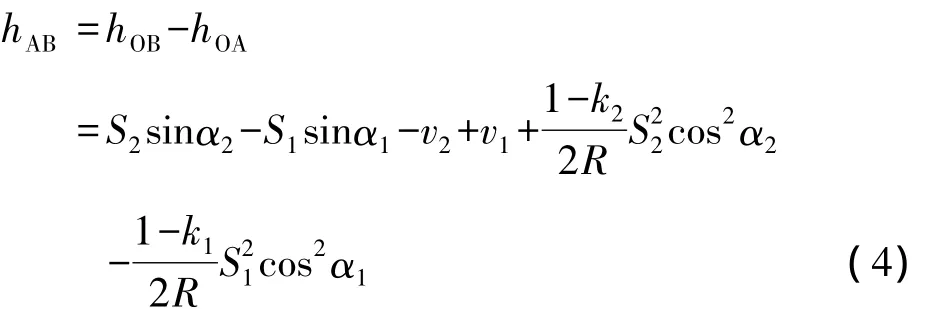
若两个棱镜高一样,则式(4)可简化为:
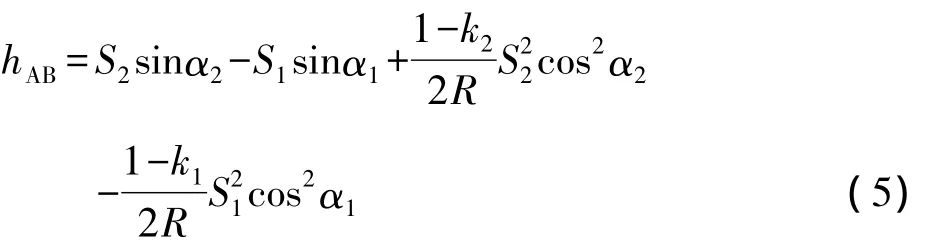
通过这种方法,可以使中间法高差的测量误差只与距离、竖直角和大气折光系数有关。
3 三角高程测量的误差来源和精度分析
3.1 单向观测的误差来源及精度分析
(1)单向观测三角高程测量的中误差
根据误差传播定律,对式(1)进行全微分,可得:

工程施工中常用全站仪的测角精度为2″,测距精度为2+2 ppm,因此,可假定:
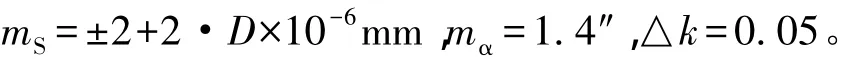
取2倍中误差为极限误差,通过式(6)及三四等水准规范可知,当 S<700 m时,三角高程可代替三等水准,当S<2000 m时,三角高程可代替四等水准。
由于k值由气象元素决定,在不同测区变化很大,故需要实测k值,确定k值通常有两种方法:
①用已知精密高差求k值

式中h1为精密水准测得高差,h2为未加球气差改正的高差,S、α、R 同上。
②同时对向观测解算k值

式中h3、h4为在两点间对向观测的高差观测值,S、α、R 同上。
(2)试验验证
为验证三角高程的实际精度,在某工程的高程控制测量中,我们分别施测了单向三角高程和二等几何水准,并将二等几何水准所测高程作为真值,与单向三角高程的测量结果进行比对。比对结果如表1所示。

单向观测三角高程测量实测精度表 表1
由表1可知,单向三角高程测量结果与真值接近,离散不明显。距离不超过 700 m时,单向三角高程能较好地满足三等水准测量的精度要求;距离在 700 m至 2000 m时,单向三角高程能较好地满足四等水准测量的精度要求,但不一定满足三等水准测量的精度要求。另外,利用实测k值计算三角高程时,所得三角高程的精度更高。
3.2 中间法观测的误差来源及精度分析
(1)中间法三角高程测量的中误差
中间法使两测段的测距误差ms相等,同时两段竖直角的中误差也大致一样,在实际测量之前应使两个棱镜高保持一致。小区域内短时间可视k值为不变量,则式(5)可简化为:
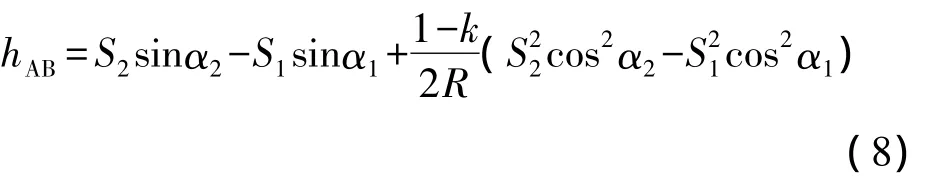
将式(8)全微分后,转化为中误差形式,可得:
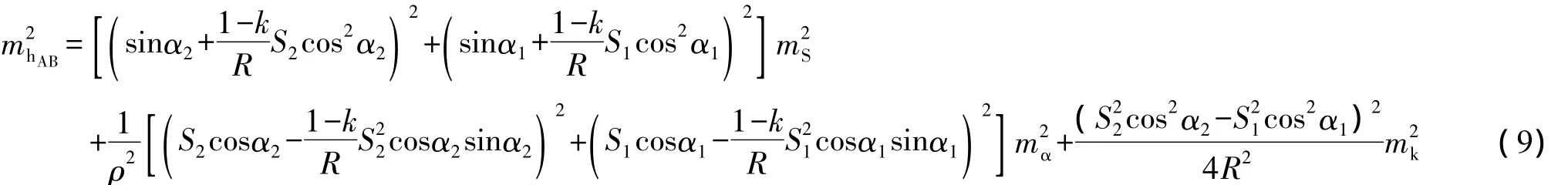
将式中微小量忽略不计,可进一步简化为:
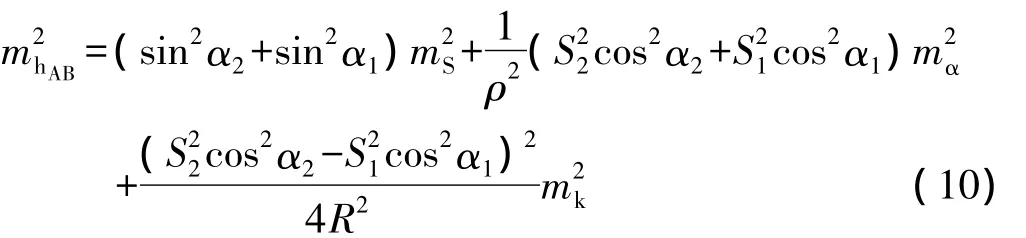
由式(10)可知,中间法高差中误差仍然主要是由距离和竖直角测量中误差决定。
(2)精度分析
假定两个棱镜高一样,由式(10)可知,中间法三角高程测量的误差来源为斜距误差,竖直角误差和k值误差,它们对高差的影响分别为:
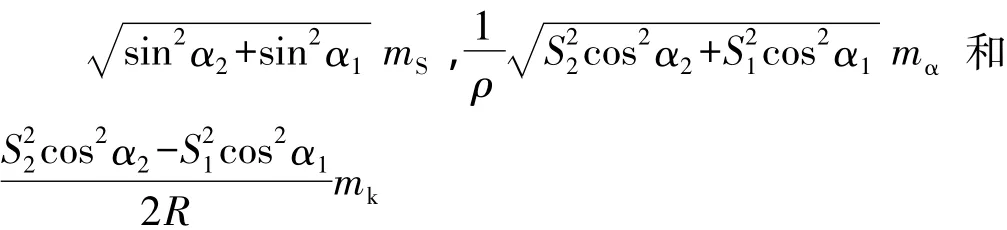
设置不同距离的测段,组合不同的两次竖直角值,得到表2为竖直角和距离分别对高差的影响量。
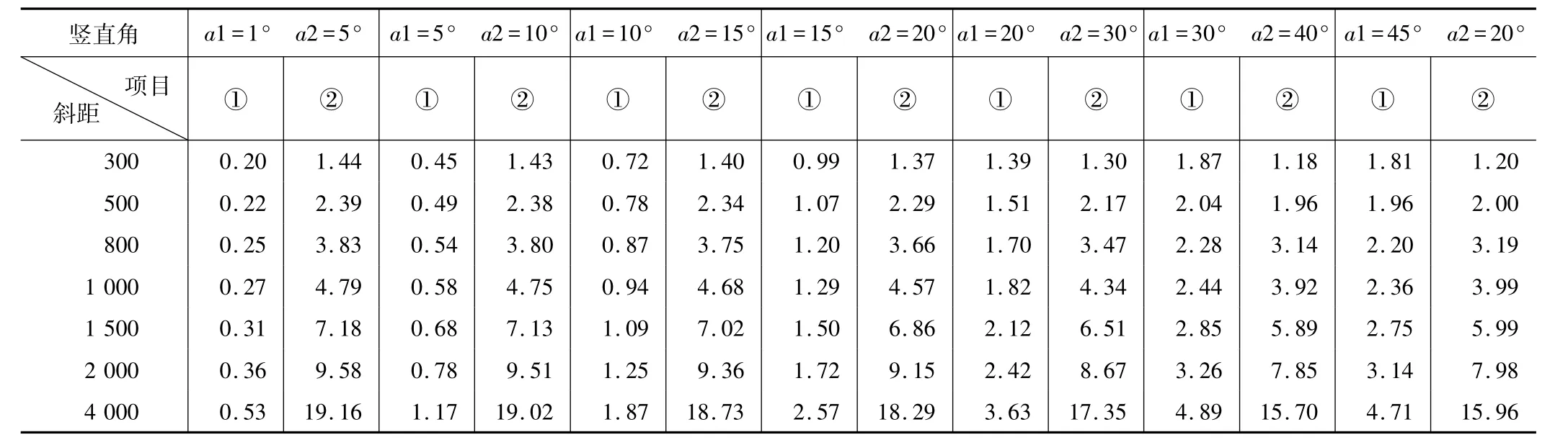
中间法观测不同斜距与竖直角时测距、测角误差对高差的影响 表2
表2表明,中间法观测的主要误差仍然是竖直角误差和斜距误差。其中竖直角误差为主要误差来源。
不考虑由棱镜高带来的误差,可得到在此条件下,中间法的高差中误差,并以2倍中误差为极限误差,可得表3。
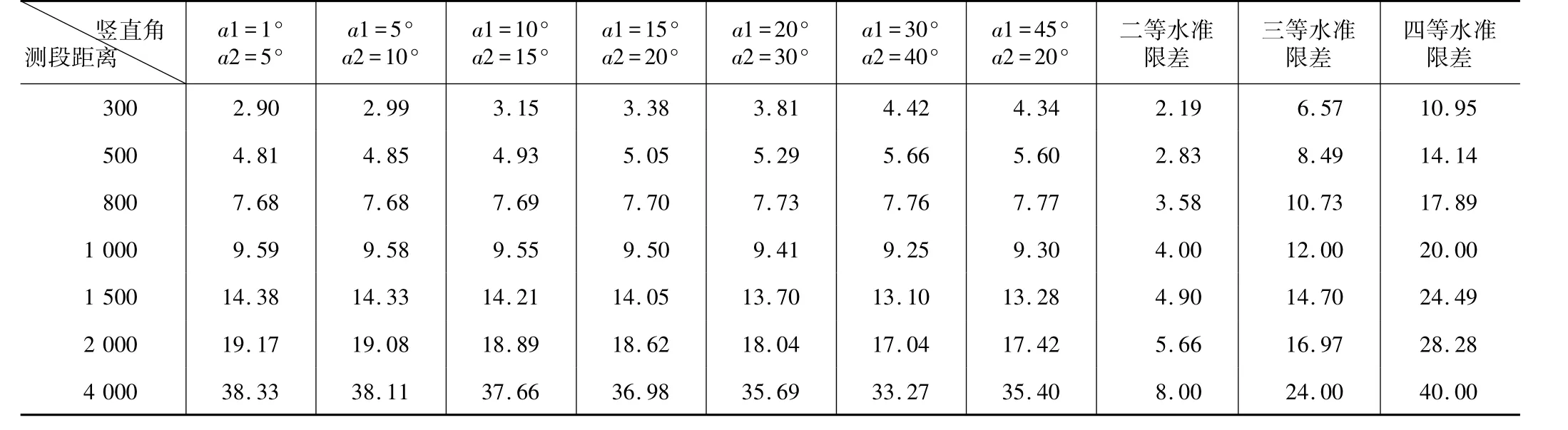
中间法三角高程极限误差与各等级水准限差比较 表3
(3)试验验证
利用二等水准和中间法三角高程测量进行实测验证,并将二等水准测量结果作为真值进行比对。测量时,前后棱镜等高,采用2″级全站仪观测两个测回,独立测距三次,成果如表4所示。

中间法三角高程测量与二等水准高程比较 表4
由表4可知,中间法观测中,当仪器架设在中间位置时,测量成果与二等水准测量高差(设定真值)进行比较,较差均很小。距离小于 1500 m时,三角高程能较好地满足三等水准测量的精度要求,但不能保证满足二等水准的精度要求。当中间法三角高程前、后视不对称时,测量误差将随前后视距差的增大而急剧增大。因此,采用中间法三角高程时,前后视距应尽量相等。
4 结语
通过以上分析和实际验证,可得出以下结论:
(1)三角高程测量中,竖直角的误差为主要误差来源,距离与高差中误差成正比;当距离一定时,竖直角与高差中误差不成简单的正反比关系;单向观测中k值要准确选取。
(2)在2″级全站仪,测距精度为2+2 ppm前提下,代替三等水准测量时,单向观测距离不大于 700 m,中间法距离不大于 1500 m;代替四等水准测量时,单向观测距离不大于 2000 m。
(3)不能将测角精度在长距离和观测条件不好时视为不变量,观测时应选择在阴天中午条件下观测。
(4)与几何水准相比,三角高程测量效率高、作业简单灵活,可作为普通高程控制测量的主要手段。
[1]张正禄.工程测量学[M].武汉:武汉大学出版社,2005(10):201~204.
[2]李青岳,陈永奇.工程测量学(修订版)[M].测绘出版社,1995(5):102~104.
[3]武汉测绘科技大学《测量学》编写组.测量学(第三版)[M].测绘出版社,1991(6):377~379.
[4]徐万鹏.对高速铁路施工测量的几点看法[J].铁道工程学报,1999(4):29~32.
[5]徐万鹏.隧道位移监测新方法的可行性探索[J].铁道工程学报,2000(2):65~67.
