GPS高程平面拟合法的应用
2014-09-22常红斌苏恒
常红斌,苏恒
(1.新疆电力设计院,新疆乌鲁木齐 830000;2.武汉市测绘研究院,湖北武汉 430022)
1 引言
目前,水准测量和三角高程测量是高程传递的两种最常见的手段,GPS水准高程拟合是众多测量专业研究的一种新的高程测量方法,也在一些工程中得到了很好的应用。常规的高程测量方法劳动强度大,投入的人力物力多,操作复杂,效率低下,发生错误时不易查找,尤其是长距离的高程传递更是非常辛苦,而GPS水准高程恰恰可以解决以上难题,简单又经济。
2 GPS高程拟合概述
众所周知,GPS高程是相对于WGS84椭球的高度,称为大地高H84,而我们常用的高程系统是正常高Hr,是相对于似大地水准面的高度,两者之间的差距通常称为高程异常ζ,三者的关系为:

似大地水准面是一个与地球形状比较接近的不规则的曲面,所以如何求得高精度的大地高和高程异常是我们大家一直探讨的问题[1]。静态GPS高程测量通过延长观测时间、增加观测时段和避开多路径效应等手段可以得到高精度的大地高。而高程异常的推算相对比较复杂,常用的方法大致可分为:①多项式曲线拟合法;②三次样条曲线拟合法;③Akima曲线拟合法;④多项式曲面拟合法;⑤多面函数曲面拟合法;⑥移动曲面拟合法等。前3种方法适用于GPS控制网布设成测线时使用,后3种方法适用于GPS控制网布设成网状时使用[2]。目前工程测量应用中最常用的是多项式曲面拟合法,此方法又分为平面拟合法和二次曲面拟合法,基本原理是:在一定区域内,高程异常呈平缓变化,利用测区内一定数量已知点的大地高和正常高求解出各点的高程异常值,将这些高程异常值近似看作一定范围内各点坐标的曲面函数,用这一函数计算其余GPS点的高程异常和正常高。这一模型函数可以表达为:

当测区内已知点数少于3个时,只能求出a0一个系数,当已知点数大于3个且小于6个时,可以求解出平面拟合中的a0、a1、a2三个系数,当已知点数大于6个时,可以求解出曲面拟合中的所有系数[3,4]。平面拟合法一般适用于高程异常变化平缓的平地或低丘地区,二次曲面拟合法适用于高程异常呈抛物单曲面地区,或似大地水准面呈两个以上凹凸面时使用,但已知点数量要达到6个以上且均匀分布于整个测区[5],所以当控制点稀少的地方且地形趋势变化不大的地方用GPS高程平面拟合的方法较适用。为此我们通过工程实例对这一方法进行了验证和总结。
3 目前工程应用
现在,大多数工程都以曲面拟合法为主。一般作业步骤如图1所示:
在选取GPS高程拟合点时应选取均匀分布于测区周围的点和具有地形特征的点,做平面拟合时至少需要3点以上,做曲面拟合时应至少选取6点以上。内符合精度是将参与计算的高程点的异常值与计算后得到的异常值进行比较,求出残差,按相应公式求解出内符合精度。外符合精度是将没参与拟合的GPS水准高程和拟合过的高程值进行比较,求解出拟合残差,按相应公式求解出外符合精度[6,8]。
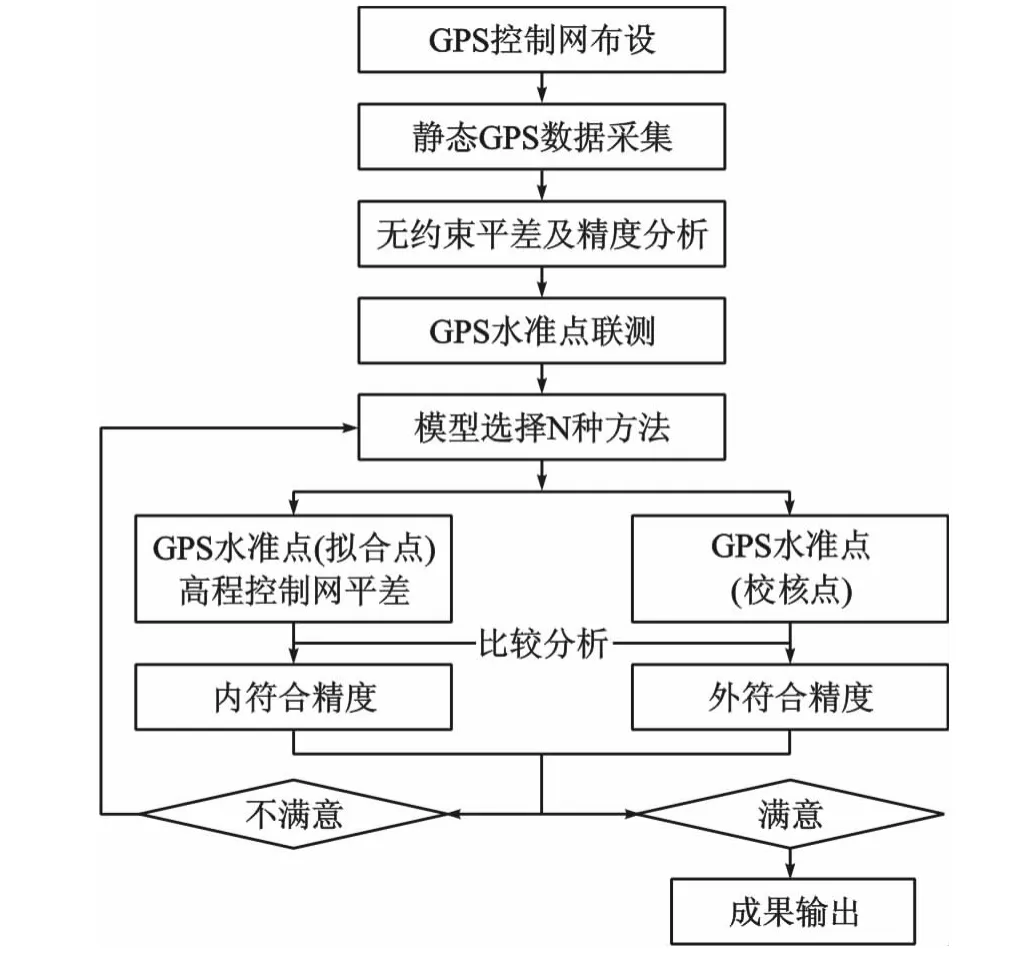
图1 GPS水准作业流程图
4 工程实例
4.1 测区概况
工程实例测区位于某市附近,由于当地控制点遭到严重破坏,且是冬天,天气寒冷,积雪较厚,为水准联测工作带来极大困难,但为验证此方法的可行性,为以后工作提供经验,作者单位还是做了四等水准的测量工作。经实地踏勘后只找到离测区相对最近的4个可靠且保存完好的控制点,其中GL与TYC为一等水准高程,YSG与GTL为三等水准高程,高程基准为1985国家高程基准,4点之间地形基本都为平地,地面起伏比较平缓,测区位于4点范围内。内业经基线解算和无约束平差后得到4个水准点的高程异常值,数据如表1所示:
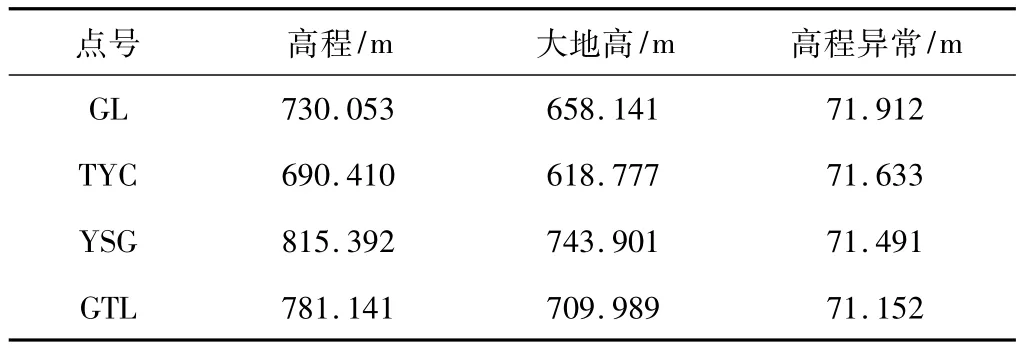
控制点高程异常值 表1
从表1可以看出该地区的高程异常变化比较平缓,4个已知水准点间距离较远,最近约为 16 km,最远约为 27 km,测区内布设E01-E05,本工程要求做测区内的控制测量工作,高程基准要求1985国家高程基准,控制网分布图如图2所示:
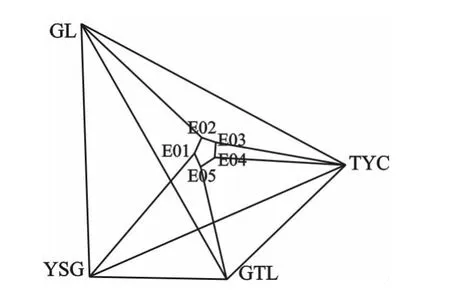
图2 控制网分布图
4.2 水准联测
本工程水准测量路线为一附合路线,顺序为GL-E01-E02-E03-E04-E05-TYC,外业施测按四等水准要求进行施测,内业采用Power Adjust 2005软件进行平差,经平差后得各点的高程值,具体过程略,数据如表2所示。

测区内高程控制点成果 表2
4.3 GPS网观测
由于收集到的控制点距离较远,所以本次外业施测均采用双时段观测,每个时段观测时间都大于60 min,使用5台双频GPS接收机进行同步观测,仪器高量测至毫米,外业观测完后对数据采用中海达软件进行数据处理,模型采用平面高程模型。
4.4 不同网形结构数据处理分析[7]
由于本次所有观测点精度相同,所以检测点就任意选取测区中的E01和E04作为检测点。
(1)选取任意一个控制点构网进行高程拟合,检查其余已知点及E01与E04,高程中误差均在 2 m左右,拟合高程数据不可用。
(2)选取任意两个控制点构网进行高程拟合,检查其余已知点及E01与E04,高程中误差均在 1 m左右,拟合高程数据不可用。
(3)选取GL、TYC、GTL三个控制点构网进行高程拟合,检查另一已知点及E01与E04,最大高程中误差为 0.004 m,测区位于拟合范围内,拟合高程可以满足四等水准测量精度要求。
(4)选取GL、TYC、YSG三个控制点构网进行高程拟合,检查另一已知点及E01与E04,最大高程中误差为 0.003 m,测区位于拟合范围内,拟合高程可以满足四等水准测量精度要求。
(5)选取GL、YSG、GTL三个控制点构网进行高程拟合,检查另一已知点及E01与E04,最大高程中误差为 0.007 m,测区位于拟合范围外,但距离拟合范围较近,拟合高程数据精度可能不满足四等水准测量精度要求,但可以满足等外水准测量精度要求。
(6)选取GTL、TYC、YSG三个控制点构网进行高程拟合,检查另一已知点及E01与E04,最大高程误差为 0.005 m,测区位于拟合范围外,但距离拟合范围较远,拟合高程数据精度不能满足四等水准测量精度要求,也不满足等外水准测量精度要求。
(7)选取4个控制点构网进行高程拟合,检查E01与E04,最大高程中误差为 0.003 m,测区位于拟合范围内,拟合高程可以满足四等水准测量精度要求。
不同网形拟合的误差统计如表3所示:

误差统计表 表3
(8)选取4个已知点和测区内任意一点或两点进行拟合,其余点拟合高程与水准高程都非常接近,误差均在毫米级,这是由于测区比较小而且比较平,所以高程拟合的精度较高。
5 结论
(1)在控制点稀少且高程异常变化平缓的区域或联测水准有困难的情况下,可以用GPS高程平面拟合的方法代替四等水准,但高程拟合至少需要3个点,且测区应分布于3个点组成的拟合范围内。
(2)对高程拟合外的高程精度将随着距离拟合面的增大而降低,不能满足四等水准测量精度要求,但距离原拟合面较近时可以满足普通水准的精度要求。
(3)对超出高程拟合外的高程中误差不可信[9]。
(4)结合以往案例和相关资料得知,GPS高程拟合的精度主要取决于:GPS大地高的精度、GPS水准联测精度、GPS水准点分布情况及数量、高程拟合模型的选择等四大因素。
在以上因素都能保障的情况下,GPS高程拟合精度可以达到四等水准测量的精度要求。
[1]徐绍铨,张华海,杨志强.GPS测量原理及应用[M].武汉:武汉大学出版社,2004.
[2]王明华,李浩.GPS高程拟合的模型优选[OL/DB].中国科技论文在线,2005.
[3]赵云,曹先密.平坦地区GPS高程异常拟合方法研究[J].测绘工程,2010,19(3):24~25.
[4]郏红伟.GPS水准测量应用探讨[J].测绘通报,2005(8):29~52.
[5]南亲江,卜建阳.GPS高程曲面拟合算法的精度分析[J].现代测绘,2008,31(4):17~19.
[6]蔡庆立.基于二次曲面拟合的区域似大地水准面确定[J].矿山测量,2010(4):24~26.
[7]伍青云.GPS高程拟合的方式及可靠性分析[J].现代测绘,2006(4):29~31.
[8]沈云中,高达凯,张兴福.GPS水准点优化选择法[J].工程勘察,2004(6):49~51.
[9]邓连利.在GPS测量中起算点对高程精度的影响分析[J].西部探矿工程,2012(5):145~146.
