GNSS接收机天线相位中心改正的影响分析

张碧波 ，李江卫，熊佑祥，孙伟

(1.天门市勘察测绘研究院，湖北天门 431700;2.武汉市测绘研究院，湖北武汉 430022;3.武汉市汉南区勘察测量队，湖北武汉 430090)

1 引言

GNSS观测是通过伪距及载波相位计算的卫星天线相位中心至接收机天线相位中心之间的距离，IGS精密星历和GNSS广播星历所给出的卫星在轨位置信息均是基于卫星的质心，而卫星质心与卫星天线相位中心存在一定的偏差，两者并不重合。另外，随着卫星的位置和高度角的改变，GNSS接收机天线相位中心与平均相位中心之间的偏差也将发生变化，因而在测量数据处理中，存在接收机天线的平均相位中心与瞬时真实载波相位中心不一致而产生的接收机天线载波相位中心偏差。根据相关研究，这种偏差可以达到 1 cm～2 cm［1，3，7］。因此，对于精密测量而言，卫星相位中心改正与接收机天线相位中心改正均是必须考虑的因素之一。本文主要针对GNSS天线相位中心改正方法及其影响进行讨论。

2 GNSS接收机天线相位中心改正

GNSS天线相位中心改正包括:天线相位中心偏差PCO(Phase Center Offset)和天线相位中心漂移改正PCV(Phase Center Variation)。PCO指的是天线平均相位中心与天线参考点ARP(Antenna Reference Point)之间的偏差，而PCV指的是天线平均相位中心与瞬时相位中心之间的变化，该变化量随着卫星的高度角、可视卫星的空间结构以及天线方位等而变化。对于高精度的GNSS数据处理，不仅要考虑天线相位中心偏差PCO、天线相位中心变化PCV、而且还要考虑GPS接收机天线整流罩(Radomes)对天线相位中心的影响［2，6，7］。GNSS 天线相位中心改正方法包括相对相位中心改正(只考虑接收机天线)和绝对相位中心改正(同时考虑卫星天线和接收机天线)。

在GNSS测量中，能够直接得到的是地面标石到天线参考点或者天线盘面上某些可量测到的几何点之间的垂高或斜高。因此，在GNSS数据处理时，首先需要将这个高度改化为瞬时相位中心与地面标石间的距离。地面标石到瞬时相位中心的高度改化H⇀分为三部分［5］，如图1 所示:

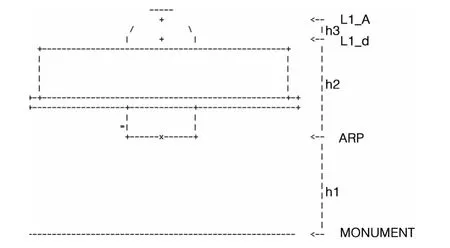
图1 天线高组成示意图

2.1 接收机天线相位中心偏差PCO

L1和L2载波各自的天线相位中心偏差值可从GNSS天线生产厂家或IGS(International GPS Service)、NGS(National Geodetic Survey)根据其天线类型查取得到。接收机生产厂家或IGS、NGS提供的相位中心偏差常用局部坐标，即天线相位中心相对于ARP的垂直方向偏差△H、北向偏差△N和东向偏差△E表示。因此，在进行改正时，需要通过旋转将局部坐标系中的偏心向量转换至地固系［2，6，7］，即:

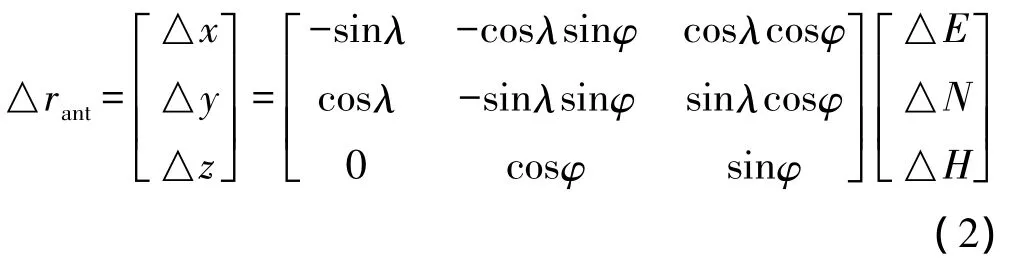
式中，λ、φ为测站的大地经度和纬度。

PCO也可以按照下式直接对相位观测值进行改正［2，6］:

式中rS和rR分别为卫星和测站在地固系中的位置矢量，λ为波长。

2.2 接收机天线相位中心漂移改正PCV

自2006年11月开始，IGS使用绝对相位中心改正模型(IGSyy_wwww，其中yy、wwww表示模型发布的年份和周)，取代至1996年开始采用的相对天线相位中心模型。绝对相位中心模型考虑了卫星天线相位中心变化，并顾及了接收机天线的方位角、整流罩的影响［2，6］，改正模型的精确性在实际高精度GNSS数据处理中得到了检验，从而被广泛应用于GNSS精密数据处理。

PCV 改正方法有以下 3 种［4，5，8］:

(1)NONE:对天线相位中心变化不进行改正，即△XL1=△XL2=0。

(2)ELEV:将PCV看成是卫星高度角的函数，采用多项式对L1和L2的单差残差进行拟合，得出由相位中心随高度角变化而引起的观测值的变化［3］，从而进行后续数据处理，即PCV为:

其中，△φ'(z)为相位中心在卫星高度角为z时的PCV，nmax为拟合多项式的最阶数，ci为拟合系数。

图2为NGS给出的某型号接收机天线的PCV随卫星高度角的L1、L2改正数及其改正残差:

图2 不同高度角PCV改正数及改正误差图

(3)AZEL:将PCV看成是卫星高度角和方位角的函数。即PCV表示为以卫星高度角和方位角为参数的球谐函数［3］，其数学表达式为:

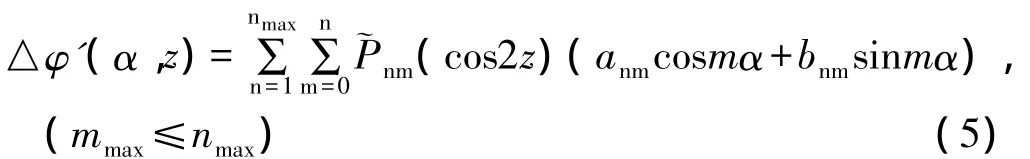
其中，△φ'(α，z)为相位中心在卫星方位角为α、高度角为z时的PCV，～Pnm为n阶、m次标准化的缔合勒让德函数，anm、bnm为谐函数系列参数。

图3为NGS给出的某型号接收机天线的PCV随卫星高度角的L1、L2改正数及其改正残差:

图3 不同卫星高度角、方位角的PCV改正数及改正误差图

按照 IGS公布的 ANTEX(ANTenna Exchange，天线数据交换格式)1.3版的说明，采用绝对相位中心改正模型时:卫星天线只考虑位于0°～14°天底角范围内的一维相位中心变化改正，改正值每隔1°给出;接收机天线同时考虑卫星位于0°～90°的天顶角、0°～360°方位角范围内的二维相位中心变化改正，这两类改正值每隔5°给出。对于非格网点上的改正，可以通过一定的算法内插得到。

在实际应用中，可根据卫星当前历元的天顶角和方位角确定天线相位中心偏差改正所在的格网，再根据四个格网点的天顶角、方位角以及相位中心偏差改正采用双线性模型内插确定该卫星实际的改正，双线性内插数学模型如下:

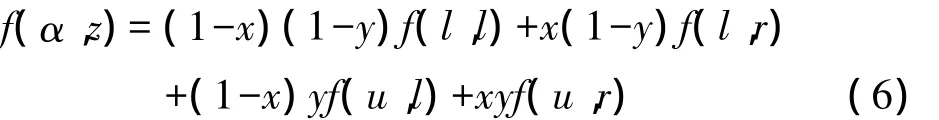
式中:f(α，z)是卫星天顶角为z、方位角为α时的相位中心偏差改正，△E为格网高度角间隔，一般为5°，z0为左下角格网点对应的天顶角α0为左下角格网点对应的方位角，△A为格网方位角间隔，其值一般为 5°;f(l，l)、f(l，r)、f(u，l)、f(u，r)分别为左下角、左上角、右下角、右上角格网点的PCV改正数值。

3 算例分析

为分析GNSS天线相位中心改正的影响，选取武汉市连续运行卫星定位服务系统(WHCORS)1 d的观测数据进行处理与分析。数据整理阶段，采用TEQC软件将 24 h的原始数据分割为两个 12 h的观测文件，采样率 10 s。接收机均为Trimble NetRS，接收机天线有两种型号，除WHKC参考站为TRM39105天线外，其余参考站均为TRM41249天线。

基线解算软件采用GAMIT10.32，分别采用RPCV(相对相位中心改正模型)和APCV(绝对相位中心改正模型)两种模式进行解算;网平差软件采用COSAGPS，固定WHCD的三维坐标，在WGS84框架下进行三维无约束平差。最终得到的其余8个参考站的坐标差值如图4所示，图中(x，y)为经高斯投影后的WGS－84平面坐标，h为大地高:

从图4可以看出:采用ELEV和AZEL两种模式进行基线解算，再采用相同的平差设置，处理后参考站的水平坐标差值较小，最大的只有 0.6 mm;高程差值明显大于平面差值，而与固定点WHCD使用不同类型天线的WHKC站高程差值要明显大于其他参考站，所有的高程差值都在 2 mm以内。

图4 APCV与RPCV解算参考站坐标差值

为分析APCV对实时数据处理的影响，选取WHKC和WHQJ两个参考站(基线长 133 km)2 h的数据进行了分析处理。图5为两测站G16、G31卫星在观测期间的高度角变化图;图6为两测站G16、G31卫星在观测期间的经PCV改正后的双差相位残余项的变化图:

图5 测站卫星高度角变化图

图6 测站PCV及其双差残余变化图

图6表明:由于天线类型不同，不同测站相同卫星经PCV改正后的差值可达 4 mm左右，基线间双差残余项的影响仍达 2 mm左右。

因此，可以认为:对于相距不远的测站(通常小于35 km)，在基线解算设置相同的情况下，天线相位中心变化双差残余项对平面坐标的影响很小，可以忽略;对于使用同类型接收机天线的测站，高程差异明显小于不同类型天线的结果，而对于使用不同类型接收机天线的测站，对高程的影响也不一样，其差异与天线性能及插值算法有关。因此，高精度GNSS测量中应尽量使用相同类型的接收机天线，并采用一定的改正算法，以削弱天线相位中心改正残差对高程的影响。

4 结语

通过以上分析，得到以下结论及建议:

(1)对于相距不远的测站(35 km以内)，卫星天线相位中心变化双差残余项的影响可以忽略;

(2)在天线定向标志指北的情况下，使用同类型接收机天线，相位中心变化双差残余项的影响较小，大多数情况下是可以忽略的;使用不同类型接收机天线，相位中心变化双差残余项的影响不可以忽略。

针对于实际工程控制测量，建议:

①为避免不同类型天线相位中心双差残余项的影响，在实际测量时，最好采用同类型天线测量，且在架设天线时所有天线的定向标志指北;

②虽然常用基线处理软件提供了多种相位中心模型选项，建议使用IGS的绝对相位中心改正模型。

［1］Markus Rothacher.Comparison of Absolute and Relative Antenna Phase Center Variations［J］.GPS Solutions，2001，4(4):55～60.

［2］Ralf Schmid，Peter Steigenberger，Gerd Gendt，et al.Generation of a Consistent Absolute Phase Center Correction Model for GPS Receiver and Satellite Antennas［J］.Journal of Geodesy，2007，81:781 ～798.

［3］郭际明，史俊波，汪伟.天线相位中心偏移和变化对高精度GPS数据处理的影响［J］.武汉大学学报·信息科学版，2007，32(12):1143 ～1146.

［4］周命端，郭际明，郑勇波等.卫星天线相位中心偏移对GPS精密单点定位精度的影响研究［J］.测绘通报，2008(10):8～13.

［5］田雪冬，郭际明，郭麒麟等.GNSS定位技术在水利水电工程中的应用［M］，长江出版社，2009.

［6］S.Y.Zhu，F.－H.Massmann，Y.Yu，et al.Satellite antenna phase center offsets and scale errors in GPS solutions［J］.Journal of Geodesy，2003，76(11－12):668 ～672.

［7］Ralf Schmid，Markus Rothacher，Daniela Thaller et al.Absolute phase center corrections of satellite and receiver antennas－Impact on global GPS solutions and estimation of azimuthal phase center variations of the satellite antenna［J］.GPS Solutions，2005，9(4):283 ～293.

［8］余龙飞，张姣姣，吴桂栋等.GPS天线相位中心偏差的削弱方法［J］.城市勘测，2013(6):106～108.