基于EDEM的掘进机后支撑腿振动造型模拟研究

王成军，何 涛，韩董董，陈 蕾，李 龙

（1.安徽理工大学 矿业工程博士后流动站，安徽 淮南 232001；2.安徽理工大学 机械工程学院，安徽 淮南 232001）

掘进机后支撑腿可防止和缓解履带的接地比压偏移及机体的侧向滑动，对提高掘进机的稳定性有着重大作用［1－2］.由于后支撑腿结构较为复杂，难以采用普通铸造成型，目前多采用焊接成型，但焊接难度大，且易变形.消失模铸造（EPC）具有精度高，无污染，无砂芯等特点，特别适合铸造内腔复杂的铸件［3－4］，因此可采用EPC法替代后支撑腿的焊接成型工艺.

振动造型是EPC工艺中的关键技术，振动造型过程中的干砂充填是一个复杂的散粒体动力学过程［5］，振动台将振动产生的能量传递给砂箱和模样进而传递给砂群，砂群因获得能量而流态化，而砂箱和砂粒之间，砂粒和模样之间及砂粒与砂粒之间的能量传递是通过接触碰撞来完成的，因此传统的分析过程中忽略砂粒间的相互作用以简化分析过程，难以反映砂群运动的真实性［6－7］.本文采用三维离散元法，在考虑接触影响的前提下，模拟不同振动方向下的干砂充填运动规律.

1 三维离散元法

离散元法（DEM）是一种计算散体物料行为的数值方法［8］.EDEM是第一个使用先进的离散元技术进行颗粒系统仿真计算的软件.传统的干砂充填分析方法仅仅局限在对竖直或水平放置的EPS模样的简单孔进行分析，而基于三维离散元法的工程应用软件EDEM可对不同姿态的复杂孔进行分析，同时EDEM软件还基于软球接触模型考虑了砂粒间的相互作用对砂群运动的影响，这种分析方法能有效提高对干砂充填运动数值计算的准确性.EDEM的软球接触模型如图1所示.模型将颗粒间的相互作用分解为法向力、切向力和滚动摩擦力矩，在上述因素的共同影响下，颗粒的运动状态发生改变［9］.通过接触力学分析可得两颗粒之间的相互作用力和力矩［10］如式（1）～（4）所示.

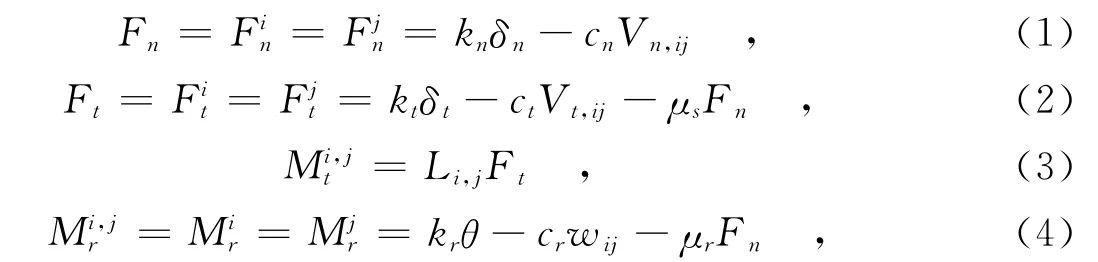
式中：F为力，M为力矩，k为刚度，δ为重叠量，c为阻尼系数，V为相对速度，μ为摩擦系数，θ为扭转变形，w为角速度，L为质心至接触点距离，n为法向，t为切向，r为滚动，s为滑动，i为第i个颗粒，j为第j个颗粒.

图1 软球接触模型

2 模拟实验

干砂充填过程与振动频率、振动时间、振幅、砂子粒径、砂子材料特性及加砂方式等因素有关，本文运用EDEM来模拟干砂充填过程，通过统计干砂充填的数目来研究振动方向对干砂充填运动的影响规律.

2.1 模拟实验装置

模拟实验装置如图2所示，运用三维建模软件建立砂箱和掘进机后支撑腿模型（即模样），将模型导入EDEM软件中，调整模型位置使填充腔Ⅰ在系统坐标系中沿YZ方向布置，即使砂箱开口方向与EDEM中Z坐标轴同向，长度方向向左与Y轴同向，宽度方向垂直纸面向外与X轴同向，并进行运动参数设定，在砂箱内顶面设置一虚拟的颗粒工厂用于产生模拟实验的砂子.

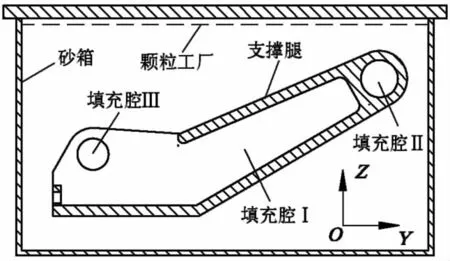
图2 模拟实验装置

2.2 模拟实验参数

结合现有的实验结论［11－13］及EDEM 数值仿真方法的特点［9，14］，确定实验参数如表1、表2、表3所示.

表1 几何及振动参数

表2 材料参数

表3 接触参数

2.3 模拟实验过程

掘进机后支撑腿振动造型的干砂充填过程如图3所示.振动造型开始时，采用雨淋式加砂0.5s，不施加振动，干砂在重力作用下自砂箱顶部的虚拟颗粒工厂向砂箱底部运动，并充填掘进机后支撑腿的周边空隙（见图3a）；加砂结束后，干砂已基本充填了后支撑腿的所有周边间隙，此时开启振动，对砂箱和掘进机后支撑腿施加多个方向的正弦往复振动（见图3b）；施加振动后，振动迫使干砂开始向后支撑腿内腔充填（见图3c）；如果施加振动合适，干砂将逐步充填砂箱及支撑腿内部的空腔，并使充填的干砂得到紧实（见图3d）.然后对关键充填部位的砂粒数目进行统计，得到不同振动方向下的干砂充填数目曲线（见图4）.

图3 干砂充填过程切片图

3 实验结果及分析

3.1 实验结果

由图4可知，掘进机后支撑腿主要填充腔有3个，其中填充腔Ⅱ和填充腔Ⅲ是水平通孔，容易充填，而填充腔Ⅰ是倾斜向上盲孔，充填困难，故本实验主要考察填充腔Ⅰ的

充填规律.图4中X、Y、Z分别表示砂箱沿X、Y，Z单向振动，XY、XZ、YZ分别表示砂箱同时沿X、Y或X、Z或Y、Z两个方向振动，XYZ表示同时沿X、Y、Z3个方向振动.由图4可知，3DOF和2DOF振动都能使干砂完全充填，且充填速度快，而1DOF振动充填时间较长，极限充填数目少，不能实现完全充填.模拟条件下振动方向对填充腔Ⅰ充填效果的影响规律如下：

（1）3DOF振动（XYZ）效果最好，2DOF振动（XY、XZ、YZ）次之，1DOF振动（X、Y、Z）最差.

（2）2DOF振动（XY、XZ、YZ）中，以YZ向振动效果最好，XZ向次之，以XY最差.

（3）1DOF振动（X、Y、Z）中，以Y向振动效果最好，X向次之，Z向最差.

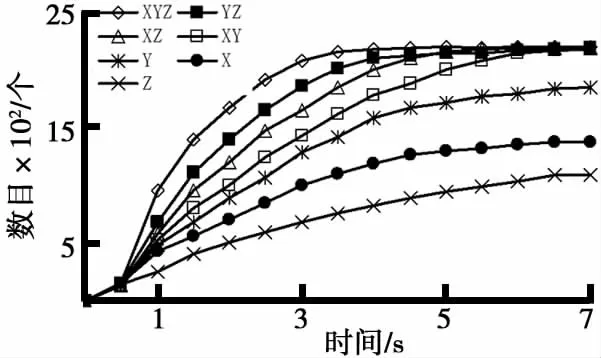
图4 干砂充填数目曲线

3.2 结果分析

由散体力学可知，砂群具有固体及流体的二象性，静止时位于砂箱上部的砂子对位于砂箱下部的砂子具有一定压力，同时砂子在振动的作用下具有振动助流的性质，振动助流有效增加了砂群的流动性，因此砂群是在砂压及振动助流的共同作用下，克服外界阻力向填充腔内部的砂群低密度区运动的.

（1）在砂压相同的条件下，3DOF振动、2DOF振动及1DOF振动的振动激烈程度依次降低，振动助流的效果也逐渐降低，故干砂充填效果也依次下降.

（2）2DOF振动中，振动助流效果相当明显，都具有较强充填能力.由于YZ振动方向与填充腔Ⅰ的走向非常吻合，同时Z向分振动有利于克服砂粒自重使砂群向上充填，因此充填效果最好；同样对于XZ向振动，由于Z向分振动的存在，其充填效果较好；而对于XY向振动，由于缺少Z向分振动，充填效果最差.

（3）1DOF振动中，振动助流作用效果已经很弱，Z向振动在克服重力的影响后，对振动助流的激励作用已经很小，所以Z向振动的振动助流效果最差，干砂充填效果也就最差；而Y向振动与填充腔Ⅰ的走向相近，有利于砂群沿着填充腔Ⅰ的内壁向盲端充填，充填效果相对最好.

4 结论

模拟实验中3DOF振动干砂充填效果最好，2DOF振动次之，1DOF振动最差；2DOF中振动中，又以YZ向振动最好，XY向振动最差；1DOF振动中，又以Y向振动效果最好，X向次之，Z向最差.采用EPC成型工艺替代掘进机后支撑腿的焊接成型工艺，并运用三维离散元法对EPC成型的干砂充填过程进行模拟研究，可快速优化干砂充填过程，缩短产品周期，降低研发成本.与传统分析方法相比，三维离散元法不仅可对不同放置方式下的复杂孔进行充填分析，同时还可计算了砂粒间的相互影响，提高数值计算的真实性，为深入研究和完善干砂充填理论提供一种新思路和新方法.

［1］赵丽娟，孙晓娜，刘旭南，等.掘进机后支撑腿的力学特性分析及结构优化设计［J］.现代制造工程，2012（9）：13－15.

［2］胡方海，王秀梅，胡建华.掘进机后支撑结构形式探讨［J］.煤矿机械，2012（6）：116－117.

［3］俱英翠，李日，刘宏伟，等.消失模铸造与普通铸造充型过程特点的数值模拟对比分析［J］.铸造，2006（11）：1 158－1 159.

［4］叶升平，郝礼，周德刚.V法铸造与消失模铸造的比较及复合铸造实践［J］.铸造，2010（6）：578－579.

［5］杨卯生，宝音，乔凤歧，等.消失模干砂紧实过程性能测试与分析［J］.铸造设备研究，1997（6）：8－9.

［6］来进勇，袁子洲，陈秀娟.消失模振动造型充填极限深度的动力学试验研究［J］.特种铸造及有色合金，2010（12）：1 135－1 136.

［7］张万红，巩济民，李锋军，等.消失模铸造工艺干砂充填垂直管的动力学分析［J］.铸造，1998（9）：9－11.

［8］Zhu H P，Zhou Z Y，Yang R Y，ct al.Discrete particle simulation of particulate systems：A review of major applications and findings［J］.Chem.Engng.Sci，2008，63（23）：5 728－5 770.

［9］胡国明.颗粒系统的离散元素法分析仿真－离散元素法的工业应用与EDEM软件简介［M］.武汉：武汉理工大学出版社，2010.

［10］何涛，王成军，张东速.基于EDEM的EPC干砂造型中的型砂运动特性［J］.特种铸造及有色合金，2013（2）：542－545.

［11］李增民，李德华，邓 宪.EPC干砂造型工艺分析［J］.特种铸造及有色合金，1996（2）：5－8.

［12］杨卯生，宝音，刘宏志.消失模铸造干砂紧实特性的试验研究［J］.铸造技术，2000（2）：42－46.

［13］冀守勋，邓金涛，张映宏，等.实型铸造干砂振动紧实性能的研究［J］.中国铸造装备与技术，1998（2）：21－23.

［14］王国强，郝万军，王继新.离散单元法及其在EDEM上的实践［M］.西安：西北工业大学出版社，2010.