一类具有两个边界层现象的奇摄动边值问题

叶珊珊，陈怀军

（安徽师范大学 数学计算机科学学院，安徽 芜湖 241000）

奇摄动边值问题的一个显著特征是小参数与最高阶导数相乘，使得因变量在越过一个非常窄的区域时经受急剧的变化，并且这些窄的区域常常毗连感兴趣区域的边界，通常称它们为边界层.处理边界层问题的方法有很多，其中包括：匹配渐近展开法、合成展开法以及多尺度方法［1－5］.例如在奇摄动边值问题［5］.

当A，B为正常数时，退化方程y2＝0不满足其中任何一个边界条件，故在区间［0，1］两端各有一个边界层.利用匹配渐近展开法，需要在x＝0和x＝1附近将边界层放大，通过引进适当的伸展变换分别求出内展开式，然后按照匹配原则将内展开式与外展开式进行匹配，得到在整个区间上一致有效的复合展开式.

本文考虑如下形式的奇摄动二阶半线性边值问题

其中ε＞0是小参数，n≥2为正整数，f（x）在区间［0，1］上连续且f（x）＞0，A和B为确定的正常数.先分析在区间［0，1］两端可能出现边界层现象的条件，利用直接匹配法（即Prandtl匹配原则）构造出在整个区间上一致有效的复合展开式，得到该问题具有边界层性质的近似解.所做工作推广了文献［5］的结果.

1 主要结果

方程（1）中小参数与最高阶导数相乘，退化方程为

因为f（x）＞0，A，B为正常数，退化方程（3）不满足（2）中任何一个边界条件，故在区间［0，1］两端各有一个边界层.我们先来寻找形式为

的外展开式.将（4）代入方程（1），并比较εo的系数，得y0（x）＝0，因此外部解yo～0.

其特异极限对应于λ＝1，上式写为

设

将（6）代入（5）和边界条件（2）的第一式，并比较εo的系数得

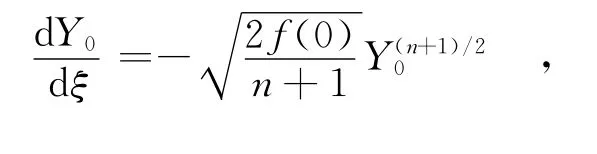
分离变量并积分得

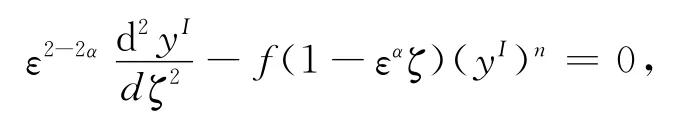
其特异极限对应于α＝1，上式写为

设yI＝（ζ）＋L将它代入（10）和边界条件（2）的第二式，并比较εo的系数得

因为

仍根据Prandtl匹配原则得到

. 于是类似上面的讨论可得

最后把内、外两展开式相加并减去其公共部分，便构成复合展开式的零次近似yc＝yo＋yi＋yI－（yi）o－（yI）o，即

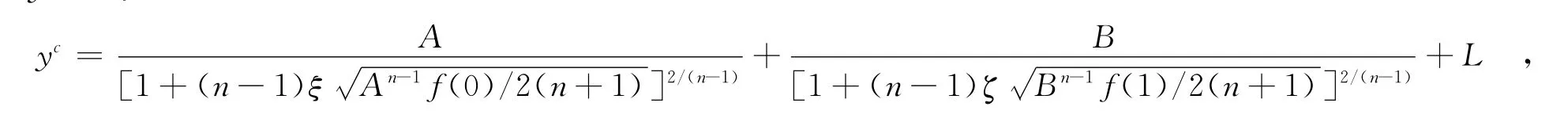
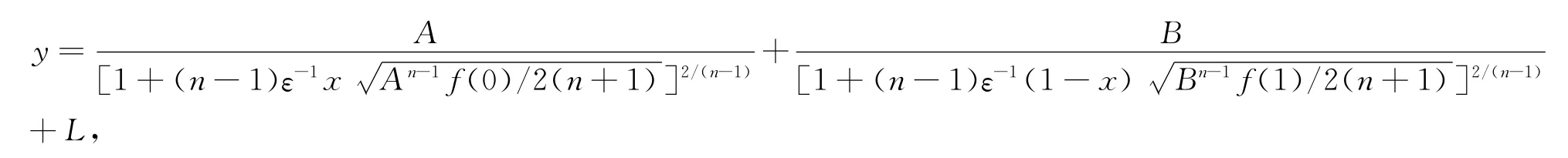
下面我们利用所得结果考虑两个特殊情形.

Ⅰ.在问题（1），（2）中，取f（x）≡1，则边值问题

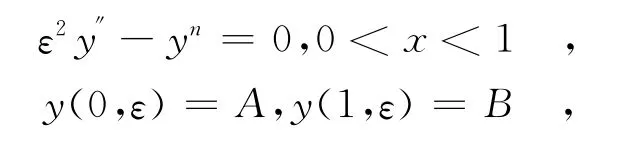
的零次近似解为

Ⅱ.在问题（1），（2）中，取f（x）≡1，n＝2，则边值问题ε2y″－y2＝0，0＜x ＜1，y（0，ε）＝A，y（1，ε）＝B，的零次近似解为

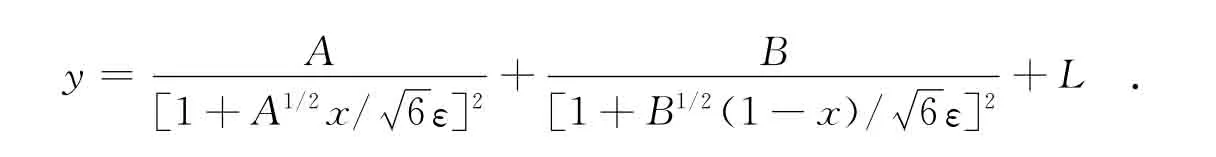
情形Ⅱ与文献［5］所得结果是一致的.

2 小结

匹配渐近展开法的基本思想是一个问题的近似解虽然不能用单一尺度的展开式给出，但可先用不同尺度的展开式分别给出，它们分别在所考虑的部分区域内有效，这些部分区域的并覆盖了所考虑的整个区域，然后再在内、外两个展开式有效区域相互重叠的部分将它们匹配，使其构成一个在整个区域内有效的近似解.人们通常应用微分不等式理论和方法研究边界层问题，通过分析微分不等式与相应的微分方程的解之间的关系，构造出一对适当的界定函数，在对所论问题的解作出先验估计的同时，也证明了解的存在性.但该方法仅给出精确解与退化解之间的一个估计，未能构造出具有边界层性质的近似解.利用匹配法则容易构造出边值问题在整个区间上一致有效的复合展开式，从而得到更精细的精确解的近似式.

［1］ 刘树德，鲁世平，姚静荪，等.奇异摄动边界层和内层理论［M］.北京：科学出版社，2012.

［2］ 陈怀军，莫嘉琪.双参数奇摄动非线性反应扩散问题［J］.物理学报，2010，59（7）：4 409－4 412.

［3］ 刘树德，孙建山，谢元静.一类奇摄动拟线性边值问题的激波解［J］.数学物理学报，2012，32（2）：312－319.

［4］ Holmes M H.Introduction to Perturbation Meyhods［M］.New York：Springer－Verlag，1999.

［5］ Nayfeh A H.Introduction for Perturbation Techniques［M］.New York：John Wiley ＆ Sons，1981.