超高层建筑结构竖向地震响应的谱单元分析

何 政，张昊强

超高层建筑结构竖向地震响应的谱单元分析

何 政，张昊强

（大连理工大学土木工程学院，116024辽宁大连）

为研究脉冲型强震中的竖向分量对超高层建筑结构动力响应的影响，针对常见的框架——核心筒体系，应用谱单元分析其简化的主结构体系模型在脉冲型强震竖向分量作用下的波动效应，并与基于振动力学的动力时程分析结果进行比较.为反映结构体系中巨型水平联系构件中剪切变形的影响，推导了考虑剪切变形的Timoshenko梁谱单元，竖向构件的轴向反应则用谱单元中的杆单元来模拟，在分析中通过对波动方程的修正来反映地震波传播的时延性.算例分析结果表明：在脉冲型强震竖向分量作用下，竖向构件的轴力波动较为明显，内部核心筒与外部巨型柱的相对错动效应显著，横向构件剪切问题不容忽视，此类损伤与后继水平地震分量作用的非线性耦合效应更须注意.

超高层建筑；脉冲型激励；竖向地震；谱单元方法；波动效应；剪切变形；Timoshenko梁

随着高度的增大，超高层建筑结构轴向刚度沿其平面分布以及楼层质量分布的不均匀性呈现加剧趋势，这些不均匀性使得结构体系对脉冲型强震中的竖向分量更加敏感，且超高层建筑的高度较大导致结构的宏观振动显著滞后.加之，相比于剪切波（S波），传递速度更快的压缩波（P波）能够在更短时间内将能量输入给上部结构，从而使结构总体抗震性能存在隐患.在近断层地区，较大V／H值（竖向分量与水平分量峰值加速度之比）或较大的脉冲型竖向地震分量均可造成这种脉冲波动效应，体现在工程结构上，可能会引起桥墩轴力的波动，进而导致其剪切承载力的下降［1］，也可能引起一些结构中不利的竖向相对错动效应［2］.对于多塔结构，其连体部分和悬臂部分的内力响应对竖向地震分量也较为敏感［3］.此外，这种分量也会使结构梁柱节点处出现较大的动应力集中［4］.

波谱单元（又简称谱单元）法是谱分析法、动态刚度法和有限单元法3种方法的优势集成，它结合了谱分析法中的波模态叠加、动力刚度法中的动力刚度矩阵形成以及经典有限单元法的矩阵装配和单元划分.谱单元是以频域波动方程为插值函数，以整个构件为一个单元，具有较高的计算精度和较好的计算效率［5］，在波传播相关研究中已有较多应用，如复合板中波的传播模拟［6］、板中损伤检测［7］、多孔介质中波的传播模拟［8］、动态裂缝发展模拟［9］等等，这些研究大多聚焦于材料层面的分析.对于谱单元法在建筑结构层面的应用也有少量进展，吴志静［10］在应用谱单元分析刚架结构动力响应时发现，谱单元方法中的傅里叶变换可能会产生周期性问题，Igawa等［11］借助拉普拉斯变换解决了这一问题，张俊兵［12］研究发现，可以在单元刚度矩阵中通过修改振动波数考虑阻尼效应.

拟针对超高层建筑结构体系中常见的框架——核心筒体系展开相关研究.考虑到核心筒与外周巨型框架柱之间横向联系构件的受力特点，结合谱单元方法，拟推导考虑剪切变形的Timoshenko梁谱单元，并通过修正波动方程以考虑P波在结构传播过程中的时间延迟，即时延性问题.为提高波动分析的计算效率，根据文献［13-14］的建议方法，拟对此类结构体系进行简化，如图1所示.

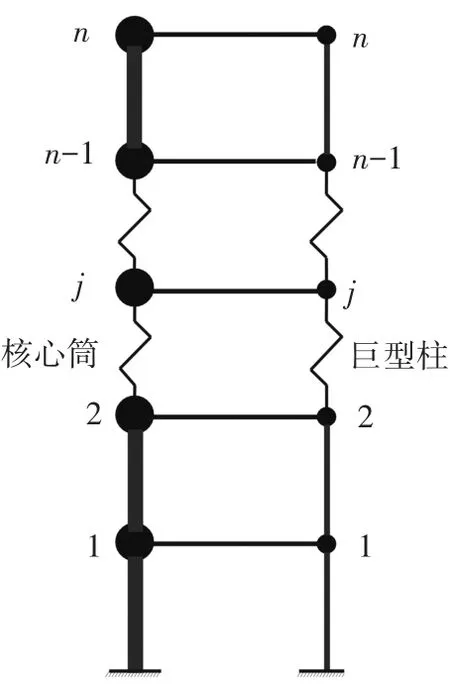
图1 模型简化示意

图1中左侧和右侧轴向构件分别代表核心筒和巨型框架柱，楼板以集中质量表示，横向联系代表联系核心筒和巨型框架柱的伸臂桁架.轴向构件采用杆谱单元［11］来模拟，Timoshenko梁波谱梁单元模拟用来模拟构件的转动变形和横向变形.由于结构竖向刚度相对较大，结构整体（尤其是主结构）进入弹塑性状态的可能性不大，加之目前谱单元方法的材料非线性问题考虑尚不够成熟，因此，本文仅考察结构的弹性波动效应，但分析结果仍有参考价值.

1 考虑剪切变形的Timoshenko梁谱单元刚度矩阵的推导

考虑阻尼效应和剪切变形的Timoshenko梁的转动和平动振动微分方程

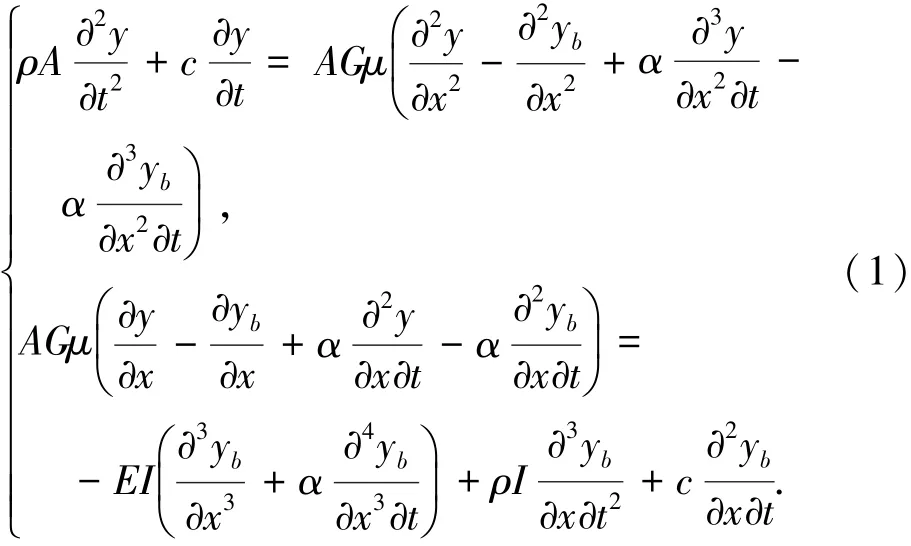
式中：y和yb分别为梁的总挠度和弯曲引起的挠度，则y-yb即为剪切变形引起的挠度；ρ为材料密度；A为截面面积；α为内部粘滞阻尼系数；μ为截面剪切系数；G为剪切模量；I为截面惯性矩；E为弹性模量；c为外部粘滞阻尼系数，参考文献［12］的作法，可直接建立波动阻尼和振动阻尼之间的等价关系，即c＝ρAa0，其中a0为比例质量阻尼常数.

为方便推导，忽略内部粘滞阻尼，即令α＝0，对式（1）作拉普拉斯变换，得

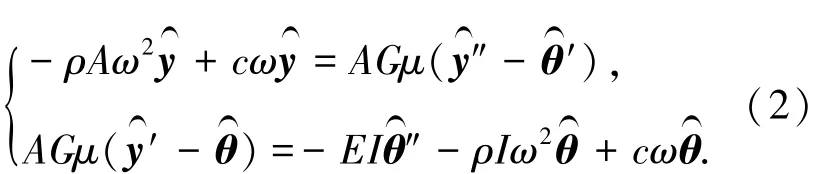
式中ω为频率.假定式（2）的一般解为

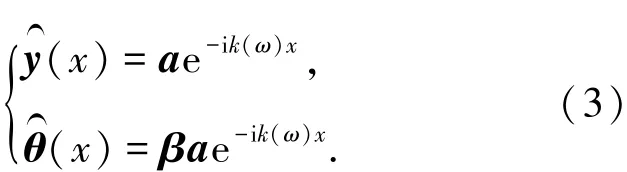
式中：a为常数向量；β为对角阵，β＝diag（βp）（p＝1，2，3，4）；k（ω）为振动波数（下文简写为k）.

将式（3）带入式（2）可得

令η1＝ρIω2／E I，η2＝ρAω2／A Gμ，η3＝cω／E I，η4＝cω／AGμ，χ＝μA G／E I，η＝η1＋η2-η3-η4，κ＝η1η2-η2η3＋η3η4-η4η1.式（4）成立的条件是其左侧矩阵行列式为零，即得

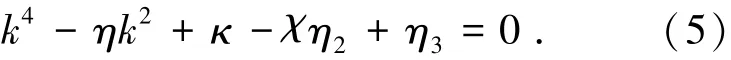
求解式（5）可得方程的根为

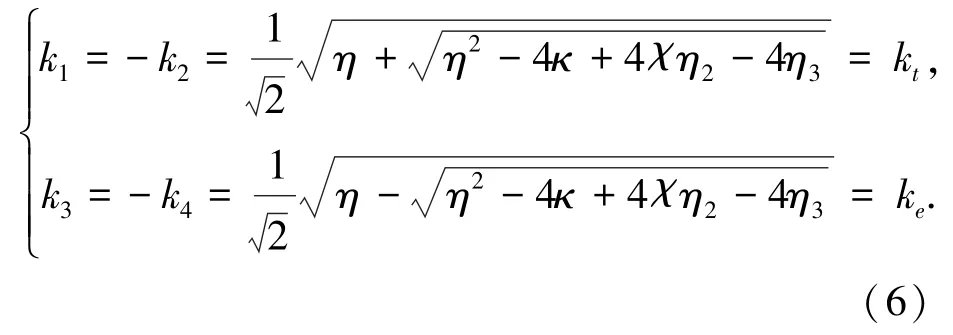
将式（6）中的kp（p＝1，2，3，4）代入式（4）中的第二式，可得βp＝（-η2＋η4）／i kp（p＝1，2，3，4）.由式（6）所得的4个振动波数来表示方程的解为

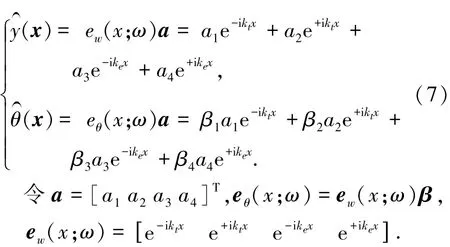
由式（7）得节点位移为

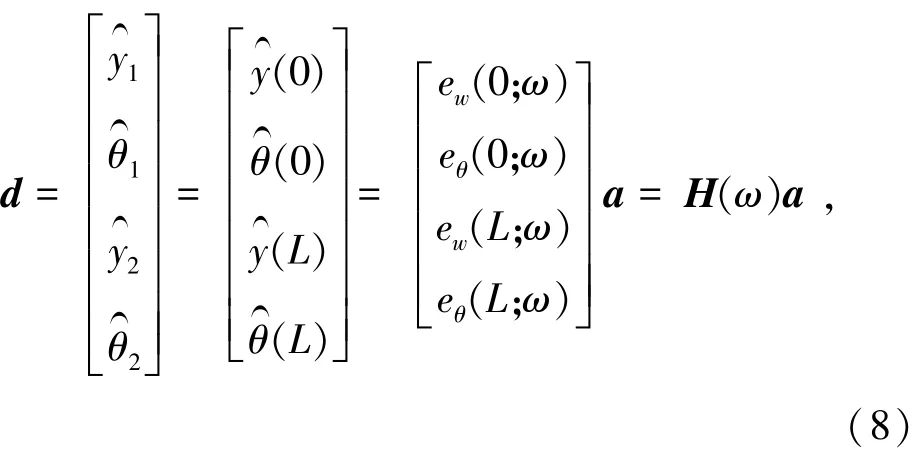
由式（8）变换得到

考虑荷载边界条件，节点荷载位移见图2.

图2 梁单元

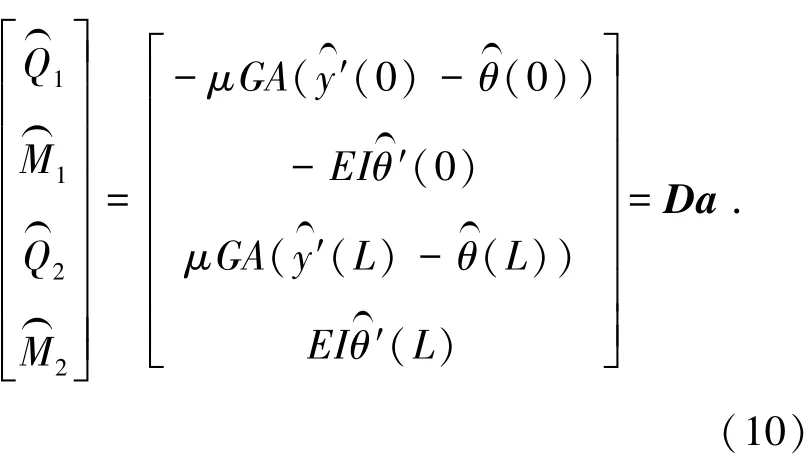
则由式（9）和式（10）结合得Timoshenko梁的谱单元刚度矩阵为

2 构件单元刚度矩阵

计算竖向地震下超高层建筑结构的动力响应，构件的轴向变形不得不考虑，因此需要在单元刚度矩阵中添加轴向变形分量.文献［12］已经推导了轴向变形构件的单元刚度矩阵：

式中kr为构件轴向振动波数.在构件单元刚度矩阵中结合式（11）和式（12）即可得到考虑轴向变形、横向变形和弯曲变形的构件单元刚度矩阵.

3 考虑时延性的动力方程

在一般动力学方程中考虑的是一致激励输入，即假定地震波同时作用于结构底部至顶部［15］，这是一种简化的作法，与事实并不完全相符.地震动在任何一种介质内部传播时都要经历一定的时间，即结构各个部分的振动在时间上存在差异，即所谓的时延性.当结构高度较低或层数较少时，这种时延性并不突出，然而对于超高层建筑结构来说，时延性的影响逐渐凸显，无论是基于传统的振动力学还是波动力学，均需要在振动方程的建立过程中作适当考虑.据此，文中假定地震波通过每层所需要的时间均为Δt（层高除以地震波传播速度），地震波到达上一层总比下一层滞后Δt，通过修正动力方程的右边项，如下式所列：

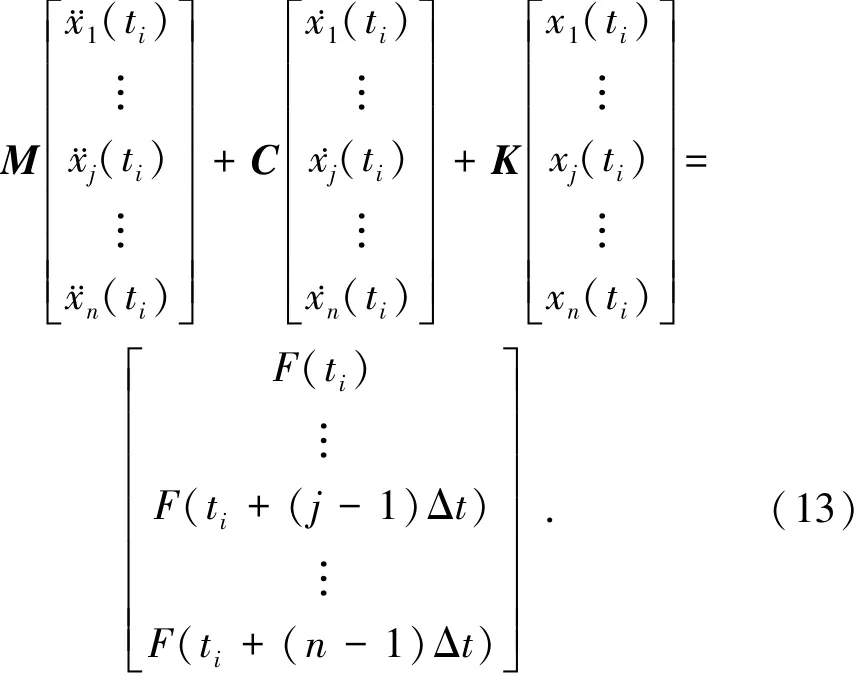
式中：M、C和K分别为结构质量矩阵、阻尼矩阵和刚度矩阵，xj是质点j处位移，F是外部动力荷载，Δt是层间传播所用时间.在进行时域修正之后，再利用拉普拉斯变换或傅里叶变换将其转换成频域荷载.

4 谱单元法计算流程

图3给出了超高层建筑结构在竖向地震作用下的谱单元分析流程，其中的拉普拉斯变换参考文献［11］的作法，借助傅里叶变换来实现，即使拉普拉斯变量s＝σ＋iω（ω是圆频率，σ是变换实常数）.采用Matlab语言进行编程，以算例5.2为例，程序由1个主程序和3个子程序构成，主程序为分析流程控制程序，3个子程序分别用来形成左侧柱、右侧柱和横向联系梁的谱单元刚度矩阵.为了保证收敛性，所有算例程序中拉普拉斯的复频常数均取为4 096个.

图3 谱单元法计算流程

5 算例分析

为验证推导的Timoshenko梁谱单元，先将其应用到悬臂梁动力响应分析，通过与理论解析解对比自振频率及自由端位移响应来考察其准确性和有效性.其后，再将其应用于一个简化的超高层框架——核心筒主结构算例，研究结构在脉冲型强震竖向分量下的动力响应，包括相对错动效应，轴力波动和横梁剪切等.算例程序均采用MTALAB语言编写.

5.1悬臂梁算例

图4所示悬臂梁的几何物理参数列于表1，梁右端作用集中荷载f（t），输入如图5所示阪神地震波，由拉普拉斯变换所得的采样时间间隔Δt＝0.01 s，实常数变换为σ＝2π／（NΔt）.通过对悬臂梁进行扫频（0～1 000 rad）得到如图6所示的频率响应曲线（简称频响图）.扫频得到的悬臂梁前三阶固有频率与式（14）给出的理论解相当相近.采用Timoshenko梁谱单元刚度矩阵和文献［12］中Euler梁谱单元刚度矩阵计算得到的悬臂梁自由端位移时程比较如图7所示，两种谱单元刚度矩阵得到的结果吻合很好，都能较准确地计算梁的动力响应，只是在极值点处稍有差异.采用两种谱单元刚度矩阵计算得到的自由端峰值位移随跨高比的变化如图8所示，当跨高比小于10时，Timoshenko梁谱单元计算的峰值位移更大.由于此类梁考虑了剪切变形，因此对于模拟一些剪切效应显著的构件更具针对性.

表1 悬臂梁参数

图4 悬臂梁

图5 阪神地震波

图6 频率响应

图7 悬臂梁自由端位移时程

图8 悬臂梁自由端峰值位移随跨高比的变化

5.2超高层建筑结构算例

图9所示一个主结构为三层的简化框架——核心筒计算模型，图9中一个谱单元代表一个主结构构件，如核心筒、巨型框架柱和作为横向联系构件的伸臂桁架，单元编号与几何参数见图9.仍以阪神地震波（图5）作为输入的竖向地震加速度时程，由于谱单元分析中频域分析耗时较多且涉及大量时域分析与频域分析的切换，计算效率较低，仅将输入竖向地震动的幅值调至200 Gal，E取40 GPa，ρ＝2 500 kg／m3，波速4 000 m／s，则两质点间40 m需0.01 s的传播时间.对于高度达到400 m的建筑，地震波在结构中传播一个来回需要0.2 s的时间，由此产生的时延性应予以考虑.

图9 简化的高层算例

如图10所示为计算得到的左侧底层质点位移时程响应（通过该质点的绝对位移时程与阪神地震动相应的位移时程相减后的结果），与图5相比发现，在峰值以及相位变化方面两图有显著差别.图10显示底层核心筒最大竖向位移约为0.3 mm，按照弹性力学可近似求解得到该部位核心筒的轴力变化为ΔN＝E AΔL／L＝6 000 kN，由此计算得到的轴压比变化约为Δn＝ΔN／fcA＝1.6%.需要指出的是，由于巨型构件轴向刚度远大于其抗侧刚度，200 Gal的地震动幅值显得偏小，如果输入地震动峰值加速度参考日本东北大地震记录到的最大竖向地震动峰值（超过1 200 Gal），则底层巨型构件的轴压比变化可能在10%左右.如果再考虑后继到达的水平分量，造成的耦合损伤可以预见.由于谱单元方法自身的计算特点，目前的应用更多聚焦于弹性分析，针对弹塑性分析的谱单元仍在发展中.

图10 左侧底层质点位移时程

图11 顶层位移差时程

根据式（15）中构件位移与节点位移之间的关系，可得图9所示左侧中间构件位移时程.

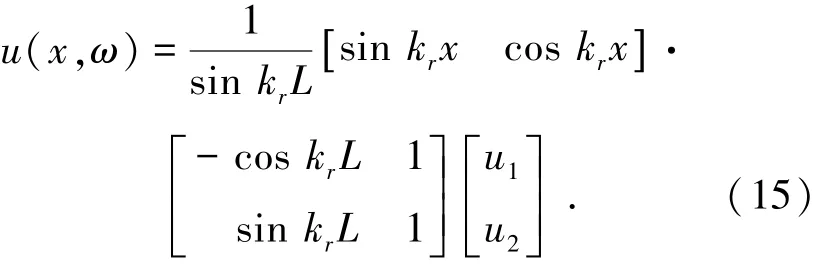
图11为不同刚度比下顶层两质点的相对位移（即位移差）时程，此处刚度比为下一层的轴向刚度与本层轴向刚度的比值［13］.由图11可见，在不同刚度比下，顶层质点位移差峰值存在相对明显的变化，且最大位移差随刚度比的增大而增大.当刚度比为100∶1时，最大位移差约为0.35 mm.类似地，如果输入地震动峰值进一步加大的话，最大位移差也将同步放大，如果地震动峰值取1 200 Gal，按照弹性分析思路来外推，最大位移差可达2.1 mm，如此大的内部核心筒与外部巨型柱的相对变形，会对连接两者的横向伸臂桁架产生累积剪切损伤，造成节点应力集中.作为保障结构体系抗侧刚度的关键联系构件，横向伸臂桁架的提前受损无疑会大大降低框架部分的框架作用，当核心筒部分和框架部分的动力特性相差悬殊时（事实往往如此），损伤将会加重.当后继水平强震分量到来的时候，这种累积损伤将降低结构的水平抗震能力.此外，图11还显示出对应刚度比为5∶1的曲线与对应其他两种刚度比的曲线存在显著相位差，这主要归因于刚度比和质点质量对入射地震能量反射和透射的影响，详细讨论见文献［13］.

本算例没有考虑轴向刚度和质量沿结构高度不均匀变化对结构响应的影响，相关影响在文献［13-14］中有详尽讨论，关于时延性的影响在文献［14-15］中均有较详细表述，在此不宜赘述.需要说明的是，算例中所取参数及得到的计算结果均是为了验证文中所提方法的有效性，在参数取值上进行了简化处理，出于计算效率的考虑，并没有直接对实际结构进行计算，这也是后续针对算法优化方面的研究重点.

6 结 论

1）在超高层建筑结构中，地震动在结构传播过程中的时延性问题需要认真考虑，无论是基于传统振动力学的平衡方程，还是以频域形式表达的波动方程.

2）推导得到的Timoshenko梁谱单元可以考虑阻尼效应，但不能直接得到阻尼系数，需要采用外部粘滞阻尼系数、内部粘滞阻尼系数与瑞利阻尼比例常数之间的关系来建立波动阻尼和振动阻尼之间的等价关系.

3）在脉冲型强震竖向分量作用下，超高层建筑结构存在较明显的波动效应，竖向结构构件的轴力存在一定的波动，尤其是底层竖向构件的轴力变化需要额外关注.内部核心筒与外部巨型柱的相对错动效应不容忽视，这种错动效应对承担横向联系的伸臂桁架影响更须重视，特别要避免与后继到来的强震水平分量作用下的损伤产生非线性耦合效应.

［1］KIM S J，HOLUB C J，ELNASHAI A S.Analytical assessment of the effect of vertical earthquake motion on RC bridge piers［J］.Journal of Structural Engineering，ASCE，2011，137（2）：252-260.

［2］黄吉锋，邵弘，杨志勇.复杂建筑结构竖向地震作用的振型分解反应谱分析［J］.建筑结构学报，2009，增刊（1）：110-114.

［3］石文龙，孙飞飞，李国强.某多塔连体高层建筑的竖向地震反应分析［J］.建筑结构，2007，34（8）：65-69.

［4］HAYASI P，MASUDA Y，HASHIMOTO S，et al.Photoelastic analysis of stress waves in building subjected to vertical impact under laboratory earthquake experiments［J］.International Journal of Impact Engineering，Elsevier，2009，36（9）：1150-1155.

［5］LEE U.Spectral element method in structural dynamics［M］.Republic of Korea：John Wiley＆Sons（Asia）Pte Ltd，2009.

［6］KUDELA P，ZAK A，KRAWCZUK M，et al.Modelling of wave propagation in composite plates using the time domain spectral element method［J］.Journal of Sound and Vibration，Elsevier，2007，302（4／5）：728-745.

［7］PENG H K，MENG G，LI F C.Modeling of wave propagation in plate structures using three⁃dimensional spectral element method for damage detection［J］.Journal of Sound and Vibration，Elsevier，2009，320（4／5）：942-954.

［8］MORENCY C，TROMP J.Spectral⁃element simulations of wave propagation in porous media［J］.Geophysical Journal International，2008，175（1）：301-345.

［9］LIU Z L，MENOUILLARD T，BELYTSCHKO T.An XFEM／spectral element method for dynamic crack propagation［J］.International Journal of Fracture，2011，169（2）：183-198.

［10］吴志静.谱元法研究杆系结构的动力学问题［D］.哈尔滨：哈尔滨工业大学，2011.

［11］IGAWA H，KOMATSU K，YAMAGUCHI I，et al.Wave propagation analysis of frame structures using the spectral element method［J］.Journal of Sound and Vibration，Elsevier，2004，277（4／5）：1071-1081.

［12］张俊兵.基于波谱单元法的结构动力分析［D］.武汉：华中科技大学，2011.

［13］何政，张昊强.简化波动方法分析结构竖向脉冲效应的反射与透射系数［J］.工程力学，2013，30（7）：153-160.

［14］何政，张昊强.竖向地震下超高层建筑结构的简化波动分析［J］.哈尔滨工业大学学报，2013，45（10）：93-99.

［15］李东升，贾辉，李宏男，等.论高耸结构地震动响应的时延性［J］.建筑结构，2010，40（增刊）：119-123.

（编辑赵丽莹）

Spectrum elements for simulating responses of ultra high⁃rise building structures excited by vertical component of impulse⁃type strong earthquakes

HE Zheng，ZHANG Haoqiang
（Dept.of Civil Engineering，Dalian University of Technology，116024 Dalian，Liaoning，China）

To investigate the influence of the vertical component of impulse⁃type strong earthquakes on the dynamic responses of ultra high⁃rise buildings，spectral elements are applied to analyze the wave effect of a simplified computational model for the main structure of typical frame core⁃wall structural system excited by the vertical component of impulse⁃type strong earthquakes.Then，the dynamic time⁃history results from this method are compared with those from classical vibration mechanics.In the wave propagation analysis，the spectral element using the Timoshenko’s beam theory is developed to reflect shear deformation in mega horizontal transverse link members.The axial responses of vertical members are modeled by rod spectral element and the dynamic wave equilibrium is modified to account for the time delay as earthquake waves propagating through structures.The results from examples analysis indicate obvious fluctuation of axial force in vertical members and significant relative displacement between core walls and external mega columns.Hence，shear problem in transverse link elements cannot be ignored.Such shear⁃induced damage would be nonlinearily coupled with the subsequent horizontal component of impulse⁃type strong earthquakes，requiring special attention.

ultra high⁃rise building；impulse⁃type excitation；vertical earthquake；spectral element method；wave propagation effect；shear deformation；Timoshenko beam

TU355

A

0367-6234（2014）08-0072-06

2013-08-05.

国家自然科学基金资助项目（90915005，91315301）；高等学校博士点专项科研基金资助项目（20120041110001）.

何 政（1971—），男，教授，博士生导师.

何 政，hezheng1971＠126.com.