砂浆泵的节能调速控制系统研究
2014-09-21赵雪松
汤 超,赵雪松
(安徽工程大学机械与汽车工程学院,安徽 芜湖 241000)
泵是一种输送液体或增加液体能量的流体机械,在各类泵中以单级单吸离心泵的应用最广,砂浆泵属于其中一种.据调查,泵的耗电量约占世界总发电量的1/4,而光单级泵的耗电量就占到总电量的1/12.面对当今工业生产节能降耗的要求,在泵行业开发出节能高效的单级单吸离心泵产品显得尤为重要.
目前人们在泵的可靠性方面研究多一些,对其节能调速控制的研究还比较少.国内尚未见到将自适应控制运用于砂浆泵的研究,也未对泵的高效转速控制范围进行分析,划分的控制范围过大,控制效果往往不能令人满意[1].市场上有一些泵的电机转速是恒定的,当遇到某些特殊工况时,需手动调节阀门,这种调节方式不够精确且劳动强度大.最主要的缺陷是这样操作即便达到工况要求,电机仍保持恒定转速.如果此时泵在低于设计流量的情况下工作,就会加速损耗过流部件并造成很大的能源浪费.
综上所述,展开对泵的节能调速控制研究具有明显的经济和环保意义.目前常用的控制方法有PID控制、模糊控制、自适应控制和鲁棒控制[2].本文采用传统PID控制和模型参考自适应模糊控制对砂浆泵系统进行仿真对比研究,比较两种控制方案的结果,选出实现泵节能调速的最好方案.
1 建立砂浆泵调速控制系统数学模型
1.1 节能调速控制系统
节能调速控制系统的框图如图1所示.

图1 砂浆泵节能调速控制系统框图
如图1所示,砂浆泵节能调速控制系统由砂浆泵、模糊控制器、变频器、转速传感器和电机组成,控制量为给定转速,被控制量为实际转速.控制过程为:比较输入给定转速与实际转速,用模糊控制器控制差值信号,将所得到的输出变量去控制变频器,变频器控制电机转速,进而达到砂浆泵的调速控制目的[3].
1.2 建立调速控制系统数学模型
砂浆泵的数学模型可简单等效为纯滞后惯性环节和带死区惯性环节的串联,表示为

式中,K为总增益,τ为纯滞后时间常数,T1为惯性时间常数,T2为变频器时间常数.
参考市场上砂浆泵实际参数,取K=20,T1=10,T2=4,τ=4.代入(1)式可得砂浆泵系统的数学模型为

1.3 建立调速控制系统参考模型
根据本文控制方法要求,需建立一个合适的与实际系统相配套的参考模型,它会影响到后面模糊控制器的性能.在这里,砂浆泵系统采用典型的二阶模型.传递函数为

根据相关参数选取原则,得到砂浆泵系统参考模型为

2 传统PID控制及仿真研究
PID是当前最常用的一种控制方式,因其控制器结构简单、控制效果不错,已有很普遍的应用.本文先用传统PID控制进行仿真研究.通过分析计算,选出一个控制效果最佳的PID控制器,在SIMULINK中搭建模型,如图2所示.仿真结果如图3所示.
由图3可以看出:系统在第1 s内无响应,运行到20 s后才达到稳定,且超调量明显较大,难以满足系统节能调速控制的要求.对于非线性、时变和参数不定的系统,传统PID无法做到精准控制,有明显缺陷,因此针对本文砂浆泵调速控制系统其控制效果并不理想.

图2 传统PID控制的SIMULINK模型

图3 传统PID控制的仿真结果
3 自适应模糊控制及仿真研究
3.1 模型参考自适应模糊控制原理
模糊控制是当前控制领域的一大热门,它结构简单,鲁棒性好,与自适应控制相结合,对于那些非线性、大时滞的复杂系统有着更好的控制效果.图4为模型参考自适应模糊控制的工作原理框图[4],在整个系统中输入信号r是一单位阶跃函数,输出信号ym为一单调上升曲线趋近于1.当对象的结构或参数发生变化时,系统的自适应机构发生作用,不断修正两个输入的增益信号E和˙E.Yp要能跟上ym,当t→∞时,有

模型参考自适应模糊控制系统原理图如图4所示.

图4 模型参考自适应模糊控制系统原理图
本文采用控制更精准的电流控制,即输入输出的信号都为电流信号.
3.2 设计模糊控制器
3.2.1 建立隶属度函数
建立e和e˙的隶属度函数:
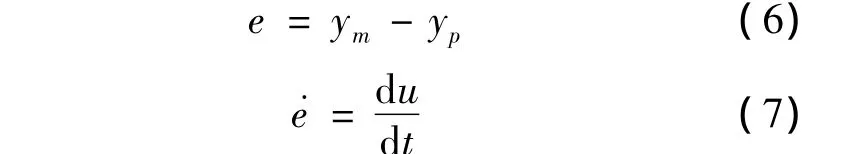
(6)式中ym和yp分别表示参考模型和实际系统在单位阶跃输入下的输出量.

(8)式中K1是输入变误差e的量化因子,(9)式中K2是误差变化˙e的量化因子,(10)式中K3是输出校正量u的量化因子.设定模糊控制器的输入输出论值域为[-6,6].在对称的隶属函数中,以钟型、梯形和三角形隶属度函数的应用最广,钟型隶属度函数相较另外两种函数,其曲线上的点平滑且都为非零点,因此本文全部选用钟型隶属度函数[5-6],则E和˙E的隶属度函数如图5所示.
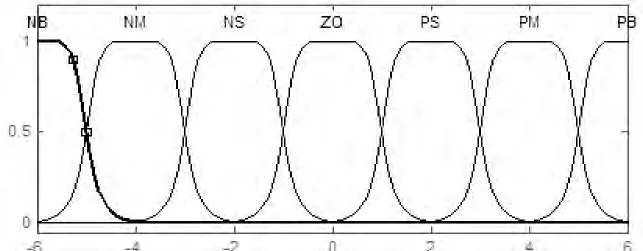
图5 E和˙E的隶属度函数
输入变量E的语言变量取值:负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB).E的隶属度赋值表如表1所示.

表1 E的赋值表
同理,输入变量˙E取值也是:负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB).˙E隶属度赋值表如表2所示.

表2 ˙E的赋值表
模糊控制器的输出模糊论域通过量化因子转化,取值为[-6,6],即 e=[-emax,emax]=[-6,6],Δe= [- Δemax,Δemax]= [-6,6].由经验得到E和˙E的基本论域分别为:
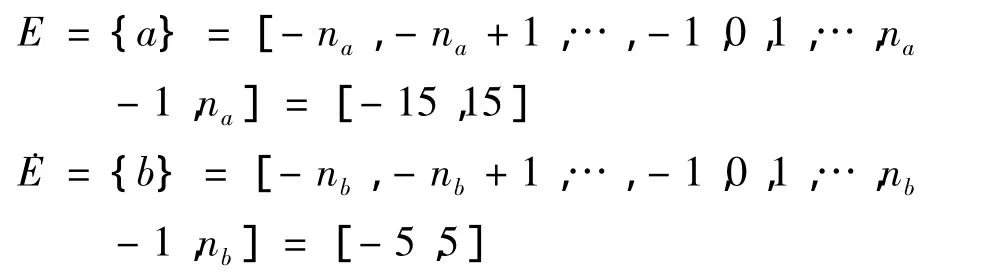
对它们量化因子,得到:

同理,根据经验取基本论域 u=[-umax,umax]=[-1,1],而模糊论域 U={c}= [-nc,-nc+1,…,-1,0,1,…,nc-1,nc] = [-1,1],这样就可求出输出变量U的量化因子K3:
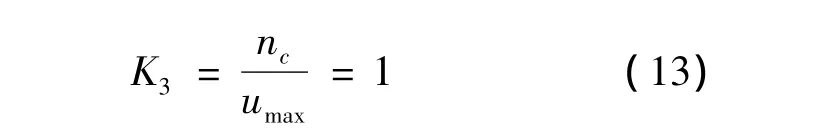
输出变量U的隶属度函数如图6所示.

图6 输出变量U的隶属度函数
输出变量 U取值:负大(NB),负中(NM),负小(NS),零(ZO),正小(PS),正中(PM),正大(PB).其赋值表如表3所示.

表3 U的隶属度赋值表
3.2.2 建立控制规则
通过以上的计算分析得出E和˙E的控制规则,如表4所示.
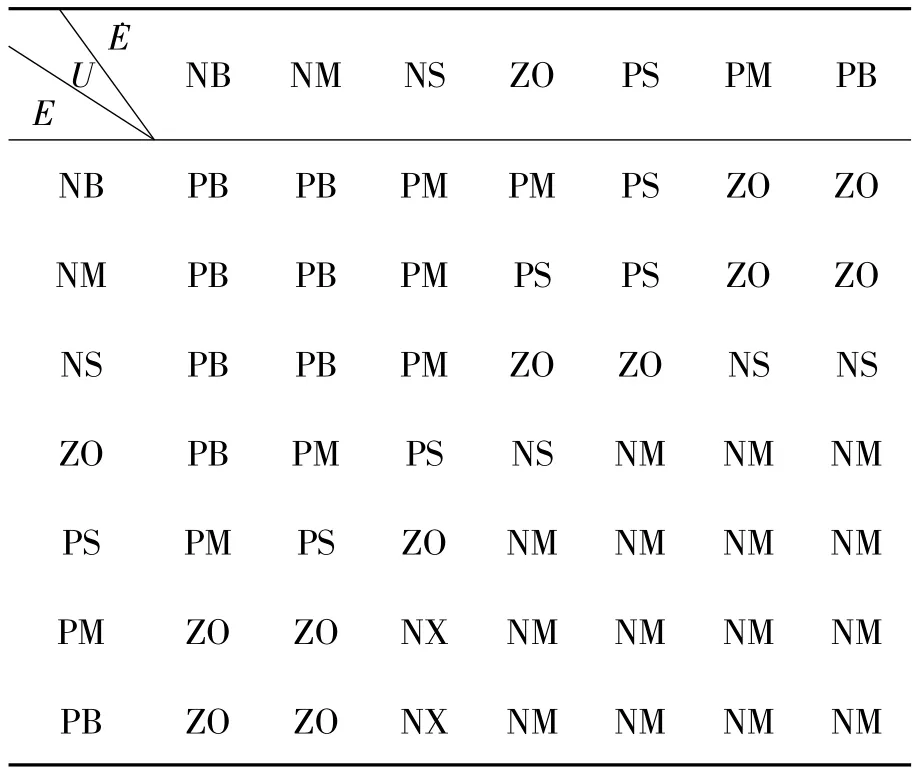
表4 E和˙E的控制规则
3.2.3 计算模糊关系
根据模型参考自适应模糊原理,输入变量,误差E和误差变化˙E要不断修正,因此它们是平行关系用“and”表示,而输出变量U用“then”表示,逻辑关系为:If E=NB and˙E=NB then U=PB.
总的模糊关系为

即:

根据以上分析,在MATLAB中建立起模糊控制器,接下来进行仿真.
3.3 自适应模糊控制系统仿真
按图4所示系统结构搭建控制系统的模型,如图7所示.

图7 自适应模糊控制系统的Simulink模型
将时间设为0~10 s,进行仿真后的结果如图8所示.横坐标为系统响应时间;纵坐标为控制量转速.

图8 模型参考自适应模糊控制仿真结果
由图8可以看出:因系统存在纯滞后环节,第1 s内无响应,到第4 s时就达到稳定,并且系统超调量较小,对比图3可以看出模型参考自适应模糊控制比PID控制的效果更理想[7-10].
4 结论
1)传统PID控制对于简单的线性系统控制效果较好,但当运用到砂浆泵这种复杂的非线性系统中时,它易受干扰而产生超调,延长系统达到稳定状态时间,超调量大,不能满足砂浆泵节能调速控制的要求.
2)模型参考自适应模糊控制将泵实际系统与参考模型的输出信号作比较,通过模糊控制器对误差划分论域,最后给出相应的控制量,最终系统在误差趋近于0时达到稳定.采用模型参考自适应模糊控制,砂浆泵调速控制系统稳定时间大大缩短,超调量小,可作为砂浆泵节能调速的控制方案.
[1]刘钊,张珊珊.变量泵控制方式及其应用[J].中国工程机械学报,2004(3):304-307.
[2]安宁,邱玮炜,戚烜.智能控制综述[J].技术与市场,2010(5):10-11.
[3]冯浩.变频调速技术在离心泵节能中的应用[J].石油化工设计,2009(3):45-47,21.
[4]摆玉龙,杨利君,柴乾隆.基于系统辨识的模型参考自适应控制[J].自动化与仪器仪表,2011(3):23-26.
[5]邢清华,刘付显.直觉模糊集隶属度与非隶属度函数的确定方法[J].控制与决策,2009(3):393-397.
[6]赵永娟,孙华东.基于Matlab的模糊PID控制器的设计和仿真[J].微计算机信息,2009(1):48-49,40.
[7]郝朝会,孙传祝,苏夏侃.自适应模糊PID控制在茶叶杀青机中的应用[J].农机化研究,2013(2):201-204.
[8]刘修廷,潘宏侠.自适应模糊神经控制系统及其MATLAB实现[J].机械工程与自动化,2010(3):162-164.
[9]徐彤,崔高健,曲永利.模糊控制集中供热控制器的MATLAB 仿真[J].区域供热,2013(1):39-42.
[10]Wu C Y,Zhao J,Zheng B C.State tracking of MRAC systems in the presence of controller temporary failure based on a switching method[J].Mathematical Problems in Engineering,2013,213:1-9.
