顶管工程管道土压力分布模式探讨*
2014-09-20黄金明
黄金明 徐 震 朱 熊
1. 上海市城市排水有限公司 上海 200233; 2. 上海市政工程设计研究总院(集团)有限公司 上海 200092
0 引言
盾构隧道、顶管等顶进式管道,在其受力分析和设计的因素中,管周土压力分布研究是关键。为了保证管道受力分析的正确性,并能更加合理、经济的设计管道方案,对管土作用体系中的管周土压力性质及分布规律进行研究具有重要意义。
近年来,国内外学者从理论分析、模型试验和现场测试等方面对管道所受的土压力进行了相关研究。在国外,Eisenstein等[1]通过实测分析,得出土压力的大小、分布与衬砌安装时间、顶进速度有关的结论;Mashimo等对隧道上的土压力荷载进行现场测试,认为浅埋隧道上土压力用太沙基土压力计算较为合理,而作用在深埋隧道上的土压力以水压力为主。在国内,侯学渊[2,3]等通过研究得出了圆形隧道轴对称情况下衬砌所受土压力的弹塑性和黏弹性解析解;周小文[4]通过对盾构隧道的离心模型试验对太沙基松动土压力公式进行了改进,并分析研究了盾尾空隙对土——结构的相互作用和土压力影响;张云[5]对埋管隧道进行了离心模型试验并结合有限元分析推求了衬砌所受的土压力;魏纲[6]等对小直径、浅覆土中顶管受力进行了现场测试,分析了管道的内力和施工前后管壁接触压力的变化;雷晗等[7]通过数值模拟对顶管管道受力模式进行了研究,并提出了建议模式。但目前在国内,对顶管工程管周土压力分布的研究并不多,大多以盾构隧道工程研究成果为参考;对现行各国在顶管设计上土压力计算模型的合理性、是否有改进的可能等也缺乏研究。本文针对顶管工程管道设计的土压力计算模型,根据对国内外顶管工程设计规范的调研结果,对现行几种土压力计算模型的合理性进行讨论、分析,并结合文献[7]对土压力分布模式进行改进性研究,提出改进的整体土压力分布模型。最后,结合工程实测验证进行了模型改进,从而为优化管道结构设计提供建设性参考。
1 国内外顶管管道受力模式调研与分析
1.1 顶管管道整体受力性状
土压力是管道设计荷载的主要组成部分,合理地确定地下管道上的土压力及其分布是进行管道设计的主要依据,是管道结构设计安全、经济的基本要求。作用于管道上的土压力实际上是周围土层与管道共同作用面上的接触应力,其大小及分布形式不仅与地层的物理力学性质、管道的刚度有关,且与施工方法、管道的埋深、直径、形状等几何参数有关。图1给出了不同规范下的刚性管道的土压力分布图。
由图1可见,土压力大致可以分为3 块:垂直土压力、侧向土压力以及地基反力。结构上部垂直土压力基本上都采用均布荷载假定。
而对于侧向土压力和底部反力以及侧向抗力各国规范都有不同的假定。
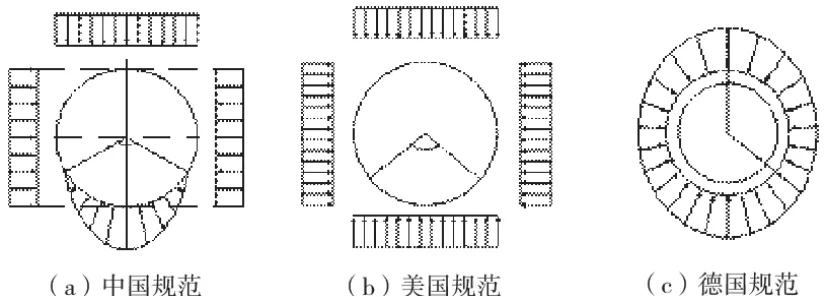
图1 国内外顶管管道受力模型
1.2 各国管道规范的土压力计算
美国规范:垂直土压力,直接采用太沙基理论计算;侧向土压力以管顶垂直土压力为基础,乘上一个与注浆有关的经验系数,均匀分布;地基反力分布模式与垂直土压力相同,具体如图1(b)所示。
德国规范:作用在钢筋混凝土管道上的土压力呈椭圆形分布,椭圆形顶点荷载确定采用太沙基筒仓模型,侧向采用经验系数法,地基反力分布模式与垂直土压力相同,均采用克莱茵分布模式,其支承角为180°。具体如图1(c)所示。
中国规程(《给水排水工程顶管技术规程》):作用在钢筋混凝土管道上的竖向土压力采用简化的太沙基模型;侧向土压力采用朗肯主动土压力模型;土弧基座采用支承角为120°的克莱茵反力假定。具体如图1(a)所示。
综上,表1给出了各国规范管周土压力计算汇总比较。
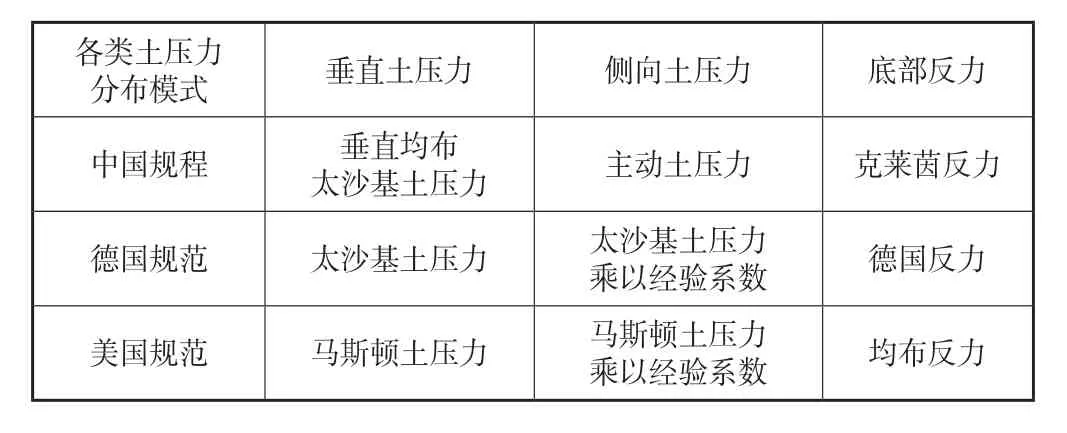
表1 各国规范管周土压力计算汇总
1.3 各种理论比较分析
从调研可见,垂直土压力、侧向土压力、地基反力等都有很多计算方法,采用哪种方法需要经过缜密的分析。
美国规范与德国规范有些类似,侧向水平土压力都引入了一个经验系数,但该系数的取值有差别。无注浆时,美国规范中的经验系数为0.25,而德国规范中为0.3;注浆体性质良好时美国规范为0.5,而德国规范为0.4。两者的地基反力分布形式也不同,德国规范中的分布模式更加均匀,而美国混凝土管道施工手册显然更具有经验性。
我国规程综合了各国规范的特点,管顶同样采用了太沙基松弛土压力。但侧向土压力采用均布的主动土压力却值得商榷,其大小和分布形式有待改进,同时地基反力的分布太过集中,使得整个结构受力相对不均匀,内力偏大。
结合工程算例:顶管内径4 m,外径4.64 m,平均覆土厚度7.6 m,主要位于土层③,土体弹性模量E=15 MPa,初始孔隙比为e0=1.18,黏聚力C=2.5 kPa,μ=0.35,渗透系数k=3×10-8,密度=1.8 kg。比较各国规范,土压力模式下管道内力见表2,其中0°、90°、180°分别指管顶、管侧和管底。
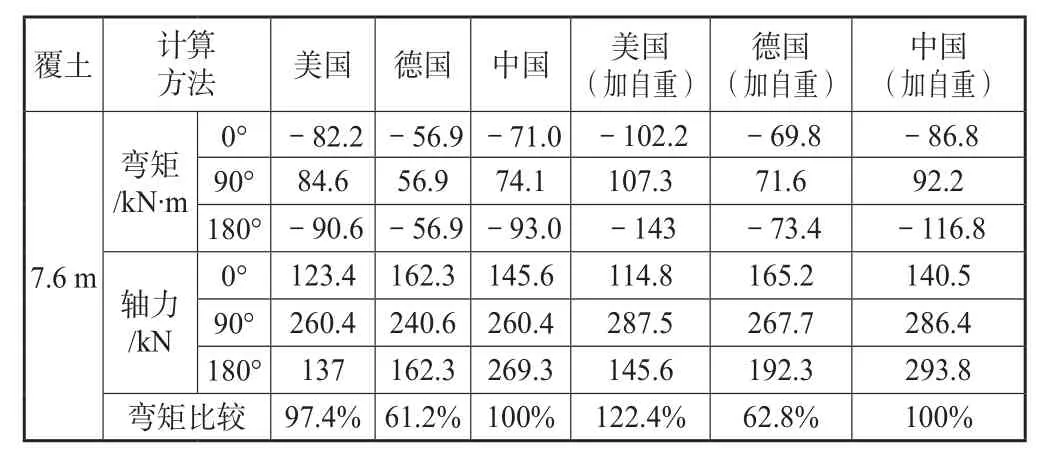
表2 管道内力比较
比较可见,美国规范计算的弯矩和轴力值略小于我国规程计算结果;德国规范计算得到的管道弯矩和轴力均明显小于中国规程计算值。因此,采用我国规程相对于其他国家规范偏于保守,计算得出的管道内力值要较其它国家规范大,这将直接导致管材消耗过大,因此有必要对我国管道土压力分布模型进行改进研究。
2 顶管管道受力计算模型改进研究
将上述各国规范管道土压力计算模型的计算值与文献[8]中关于管道受力特性的数值模拟结果进行对比可见,各国规范规定的管顶垂直土压力分布模式的计算值都接近文献[8]有限元计算结果,明显的差异主要体现在管侧和管底土压力。其中,德国规范土压力分布基本被有限元包住,两侧略小;美国规范和我国规程的两侧土压力计算值明显小于文献[8]有限元计算结果;我国规程管底土压计算值最大。基于以上对比,可对侧向土压力分布模式和管底土反力分布模式分别加以改进,进而提出改进的整体土压力分布模型,使计算结果更加符合实际。
2.1 管侧土压力分布模式的改进
图2给出了文献[7]模拟的有7.6 m覆土顶管的接触压力换算的管道侧向土压力和我国规程采用的拱内主动土压力计算的侧向土压力的比较,可以看出,采用有限元计算得到的结果相对于我国规程在侧向土压力上有较大的增加。
在上述分析基础上,提出管道侧向土压力的取值按照图2(图中虚折线)所示,划分为2 个分段函数,其中:
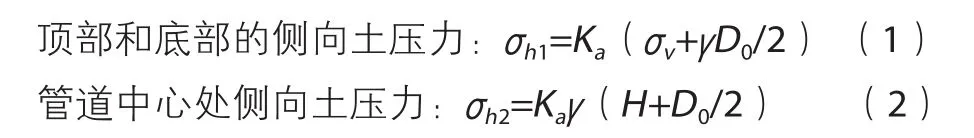
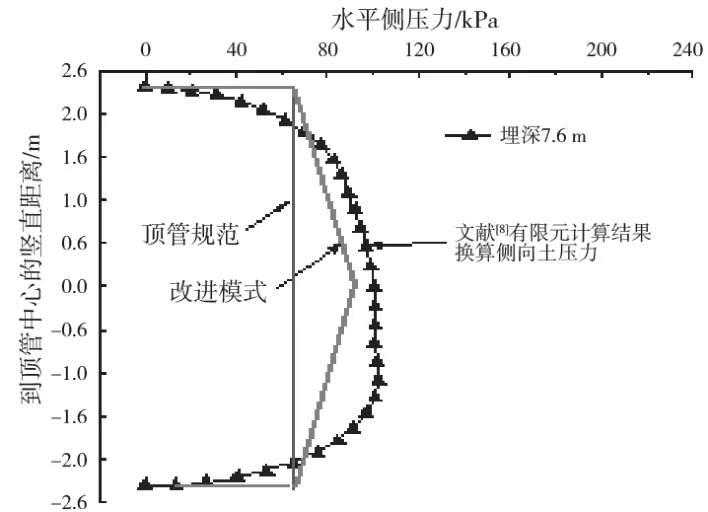
图2 顶管侧向土压力改进模式
为了判断改进后的侧向土压力分布模式是否合理,在我国规程的基础上,我们不改动管顶竖向土压力和地基反力分布,而在侧向均布土压力基础上加上一个三角形荷载,如图3所示。根据该模式结合上文算例计算管周接触压力(不计管上腔内土重和管内满水作用),结果如图4所示。可见,侧向加三角形荷载后管土接触压力仍没有文献[7]有限元结果均匀,但相对于我国规程,改进模式的侧向接触压力增加、底部接触压力变化不大,能对管道设计进行一定的改进。
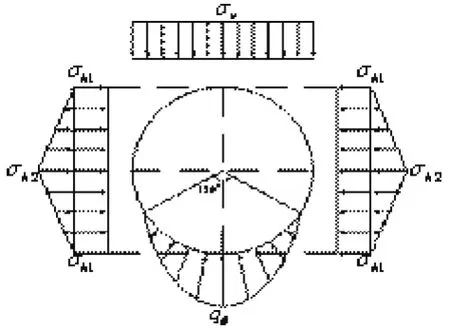
图3 规程[11]侧向加三角形荷载
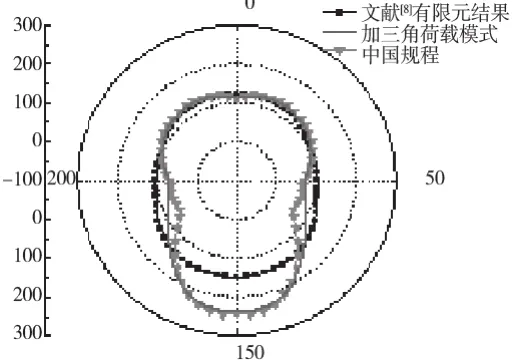
图4 侧向土压力对比
2.2 地基反力分布模式的改进
地基反力属于被动抗力,其分布形式既与上部荷载的分布形式有关,又与下部土层条件有关。我国规程和德国规范中均采用克莱茵分布模式,而美国规范采用均布模式,且支承角不一致,三者之间的差距明显。
我国规程的地基反力假设都比较大,由于外荷载分布的不均匀会使得管道产生较大弯矩,在我国规程的地基反力模式下设计管道,需要考虑较大的管道内力设计值。
结合上文算例,重点讨论法向力,将我国规程假定的支承角2φ=120°、德国规范规定的支承角2φ=180°的克莱茵反力分布模式计算结果,与文献[7]的有限元计算结果进行比较,支承角2φ=120°克莱茵分布模式的计算值与有限元的计算值相差比较明显,在120°~240°范围内地基反力由0~242 kPa,分布很不均匀。而180°角克莱茵分布模式的计算值在90°~270°内地基反力为0~148 kPa,其分布较前者要均匀很多。三者之间的差别一方面为有限元计算与理论计算本身的差别,另一方面则在于理论计算中忽略了支撑角以外部分侧向压力对于管片的压力。由此可以判断,基底反力计算的差异主要在于支承角度的取值问题。有关测试与研究表明,基底反力的分布与基底土层性质有关。美国规范中对于不同土层建议采用不同的基底反力支撑角,我国规程建议取120°克莱茵反力分布模型,其主要适用于土质条件较好的地基中。而支承角为180°的克莱茵反力分布模型更适合软黏土层地基。
考虑基底土层影响并与现行规范保持一定连贯性,对管道下半部分的法向土压力分布模式,采用如图5所示的圆弧状,即支承角为2(90°-φ)=(180°-2φ)的克莱茵反力分布模式加以改进,且(180°-2φ)不小于120°。
2.3 改进的整体土压力分布模型
综合上述对管侧土压力和管底地基反力分布模式的改进分析,我们将管侧土压力分布考虑为分段线性、地基反力扩大至(180°-2φ),从而提出了更符合文献[7]数值分析结果的土压力分布模型,如图6所示。
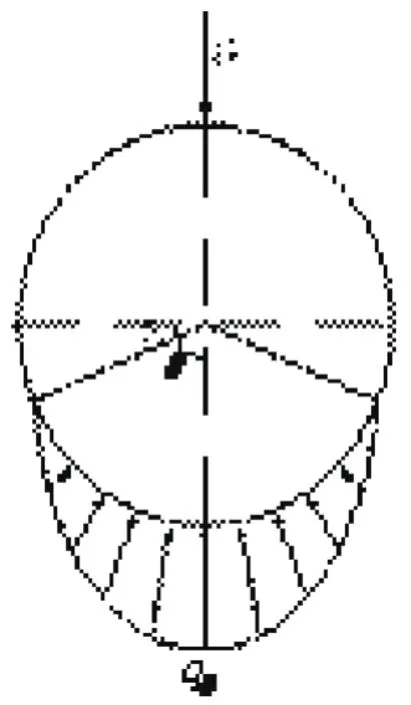
图5 地基反力分布改进模式
不计管上腔内土重和管内满水作用,仍结合上文算例分析,图7给出了改进后整体土压力分布模型的计算结果与我国规程和文献[7]有限元计算结果的对比。从中可见,改进后的整体土压力分布模型计算结果,仍没有文献[7]的有限元计算结果均匀,但相对于我国规程,管侧土压力有所增加,仍小于有限元计算值;管底反力有所减小,却仍大于有限元计算值。因此,改进后的模型既能有效地减小管道内力,同时仍保证了一定的安全度。
2.4 结合工程实测验证改进模型
结合上海市污水治理白龙港片区南线输送干线完善工程(东段输送干管)实施过程中的测试标段顶管施工,进一步验证提出的改进模型。
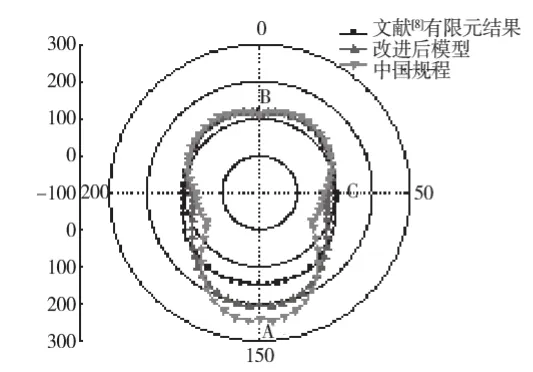
图6 整体改进模式
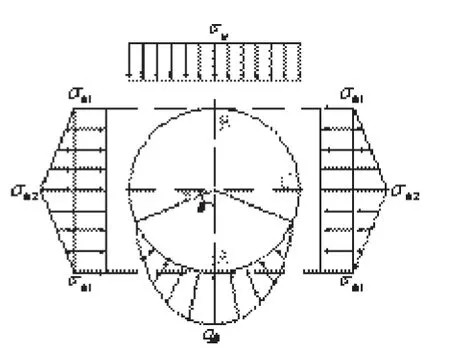
图7 管土接触压力对比
该工程顶管内径为4 000 mm,外径为4 640 mm,顶管底埋深14.0~15.0 m,管道材质为钢筋混凝土预制管,每节管长度为2.5 m。测试标段1顶管平均覆土厚度7.6 m,土层信息同上文算例。测试标段2顶管平均覆土厚度10 m,位于土层④,土体压缩模量Es=2.3 MPa,初始孔隙比e0=1.43,黏聚力C=11 kPa,泊松比μ=0.35,渗透系数k=3×10-8,密度=1.68 kg,内摩擦角10.8°。
表3给出了2 种覆土厚度条件下顶管实测结果和不同土压力分布模型的计算结果。对比可见,实测管周土压力相对均匀,形态上与文献[8]有限元模拟的结果的分布形态相近;美国、德国规范的管顶、管底土压计算值与实测结果很接近,所有模式的管侧土压计算值都小于实测结果;改进模型计算的管底土压较我国规程略有减小,管侧土压稍有增加,可适当的减小管道内力设计值,差异大小主要由土层条件决定,虽然德国规范和美国规范与测试结果更加接近,但从结构安全设计角度来看,改进模式更适用于优化管道结构设计。
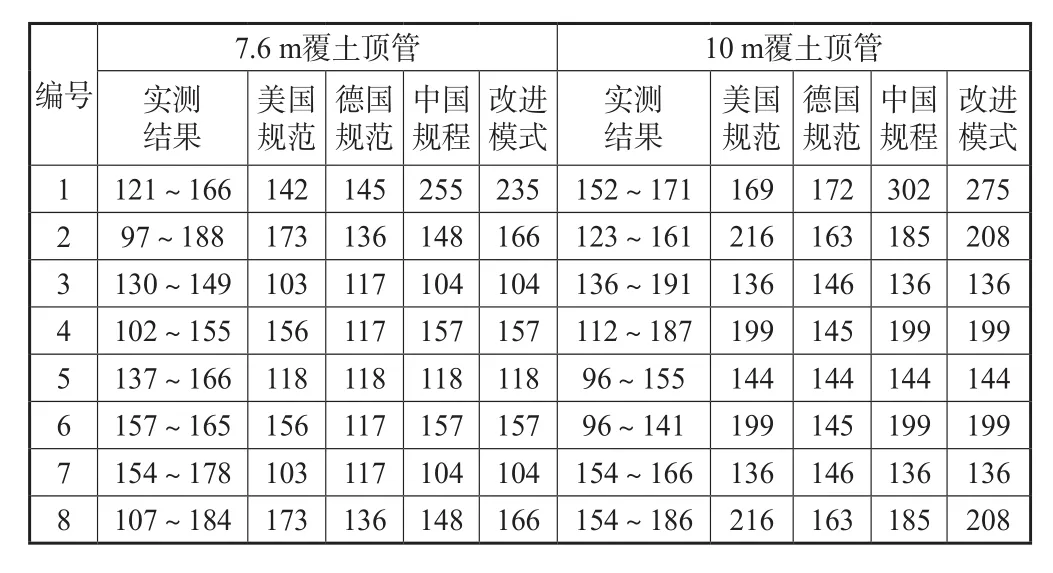
表3 顶管实测结果与各类土压力分布模式对比 单位:kPa
3 结论
本文从理论上对顶管所受土压力的分布模型进行了研究,并结合文献[7]的研究结果和工程实测分析,得出结论如下:
(a)美国与德国规范相比,侧向土压力计算都引入了经验系数,但各自取值有差别;两者的地基反力分布形式也不同,德国规范中的分布模式更加均匀,而美国混凝土管道施工手册显然更具经验性。我国顶管规程综合了各国规范的特点,但侧向土压力采用均布的主动土压力,地基反力的分布太过集中,使得整个结构受力相对不均匀,内力偏大,用于管道设计偏于保守。
(b)管侧土压力分布模式采用在我国规程规定的管侧土压力分布模式基础上加上1 个三角形荷载;考虑管底土层的影响,管底采用支承角为2(90°-φ)=(180°-2φ)的克莱茵反力分布模型;综合提出的改进后的整体土压力分布模型计算结果,虽没有文献[8]有限元计算结果均匀,但可以适当地减小管侧和管底的设计内力。
(c)工程实测结果表明:实际管周土压力分布较为均匀,并验证了改进模型的合理性,可以为优化管道结构设计提供建设性参考。
