基于断路器零阻抗特性的PMU量测状态估计方法

陈 亮，毕天姝，薛安成，杨奇逊

（华北电力大学 新能源电力系统国家重点实验室，北京 102206）

0 引言

同步相量测量单元PMU（Phasor Measurement Unit）能够监测系统动态过程[1-6]，在电力系统动态安全监测中得到了广泛应用。然而，由于互感器和通信系统噪声的影响，PMU量测量不可避免地存在随机误差，这可能使得PMU无法准确监测系统动态过程，甚至导致控制系统给出错误的控制指令。因此，针对PMU量测量，开展系统动态过程的状态估计方法研究对进一步推广基于PMU的应用具有重要价值。

已有计及PMU量测信息的电力系统状态估计研究[7-10]主要针对PMU应用初期系统可观性不足问题，结合测控终端 RTU（Remote Terminal Unit）的量测，进行混合非线性状态估计。这些方法尝试利用高精度PMU量测信息提高传统静态断面状态估计的精度，没有涉及系统动态过程量测信息精度的提升。

近年来，我国500 kV及以上电压等级变电站和100 MW及以上发电机均装设了PMU，这使得完全基于PMU量测的状态估计成为了可能。文献[11-12]提出一种变电站-调度中心两级分布式线性状态估计的体系结构和方法，但该方法仍针对的是静态状态估计问题，不涉及系统动态过程。

然而PMU主要用于系统动态过程监测，而且系统动态条件下电气量变化范围更大、电磁环境更为复杂，PMU量测受各种干扰因素影响造成随机误差的可能性更大。因此近年来，基于PMU量测的系统动态过程状态估计方法逐渐引起人们的关注。文献[13]给出了一种系统机电暂态过程中分布式发电机动态状态估计方法。由于系统故障后的动态过程中，网络拓扑可能发生变化，且难以实时获得，传统的集中式状态估计方法无法适用。如何提升系统动态过程中变电站内PMU量测的精度仍是一个悬而未决的问题。

本文针对故障后网络拓扑改变，集中式状态估计不再可行的问题，提出适用于动态过程的分布式状态估计框架；并在系统发生故障后，断路器状态未知的情况下，根据断路器零阻抗特性构造了断路器的非线性零阻抗虚拟量测方程；进一步建立了动态过程中考虑断路器零阻抗特性的状态估计模型，推导了雅可比矩阵的具体形式，并采用非线性加权最小二乘 NWLS（Nonlinear Weighted Least Square）对模型进行求解。将所提出的状态估计方法应用于IEEE 39节点测试系统，结果表明，该方法不但具有良好的滤波效果，还能够对断路器的状态进行判断。所提算法满足应用的实时性要求，具有一定现实意义。

1 分布式状态估计总体框架

电力系统发生故障后，断路器动作，状态改变，难以实时获得动态状态，传统的在调度中心基于网络拓扑结构进行集中式状态估计的方法已经不再可行。这就需要研究动态过程中，断路器状态未知情况下的电力系统状态估计的框架结构。

针对上述问题，本文构建了一种电力系统动态过程中分布式状态估计框架，如图1所示。该框架结构主要包括3个部分：发电厂内的发电机状态量动态状态估计、变电站内的计及零阻抗特性状态估计和调度中心全网状态估计。

发电机状态量动态状态估计主要利用系统动态过程中发电机转子内在惯性使得发电机状态量不能突变的特性作为约束，进一步提升估计精度，这部分研究工作已经取得成果[6]。变电站内状态估计主要针对故障后断路器状态未知情况下，在变电站内利用PMU量测信息和断路器零阻抗特性对节点电压和断路器电流相量进行估计并确定断路器状态；将估计后的熟数据以及静态数据库中的拓扑信息上送至调度中心进行全网状态估计。这部分研究工作将在本文展开。调度中心的全网模型静态数据库含有系统中所有变电站、发电厂以及线路的拓扑信息。调度中心的全网数据整合单元利用这些拓扑信息对各个变电站和发电厂上送的估计结果和变电站模型静态数据进行整合，得到全网的节点-支路拓扑结构以及节点电压和支路电流相量，最后进行全网线性状态估计。全网状态估计的难点在于全网数据整合，后续工作中将对此展开研究。

图1 分布式状态估计架构Fig.1 Frame of distributed state estimation

2 基于零阻抗特性的状态估计模型

2.1 断路器模型

电力系统状态估计的基本原理就是利用量测冗余度对系统状态量进行估计。变电站中存在的断路器阻抗很小，在对其建立数学模型的过程中，可以假设断路器阻抗为0。如果利用该特性进行状态估计的虚拟量测则可以更进一步提高冗余度，从而提升估计精度。将变电站中每台断路器都作为变电站拓扑结构中的1条支路，断路器两侧分别作为2个节点建立模型。假设变电站中某断路器编号为k，两端节点编号分别为i和j，其模型如图2所示。由于断路器阻抗为0，如果仅仅将节点电压相量作为状态变量，则无法得到电流量的估计值。针对该问题，将断路器两侧节点电压幅值和相角以及断路器支路电流实部和虚部同时作为状态变量，则状态量x为：

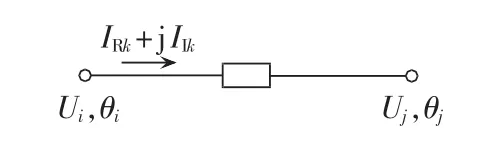
图2 断路器模型Fig.2 Model of circuit breaker

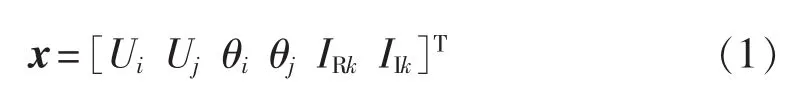
其中，Ui、Uj和 θi、θj分别为断路器 k 两端节点 i和 j的电压幅值和相角；IRk和IIk分别为流过断路器k的电流的实部和虚部，规定电流正方向为从断路器两侧编号较小的节点流向编号较大的节点。

在系统运行过程中，断路器有断开与闭合2种状态。系统故障后，断路器状态发生改变，难以实时获得，此时，断路器实际状态未知。根据对断路器状态的掌握情况将断路器分为闭合、断开和状态未知3种类型，数量分别为N1、N2和N3。分别对这3种类型的断路器建立模型。

a.闭合型断路器（k=1，2，…，N1）。 由于断路器阻抗为0，闭合断路器两侧节点电压的幅值差和相角差必然为0，即：

b.断开型断路器（k=N1+1，N1+2，…，N1＋N2）。流过断开型断路器的电流必然为0，即：

c.状态未知的断路器（k=N1+N2+1，N1+N2+2，…，N）。发生故障后，断路器状态发生改变，如果断路器的实际状态无法实时获得，则式（2）和（3）的约束条件就无法继续使用。然而，由于断路器阻抗为0，若断路器闭合，则其两端节点电压的幅值差和相角差为0；若断路器断开则没有电流流过，则其电流实部和虚部为0。因此，无论断路器处于何种状态，断路器电流相量与两端节点电压幅值差和相角差的乘积总是为0。利用该特性，将断路器电流实部和虚部与两端节点电压的幅值差和相角差分别相乘，构造断路器状态未知情况下，零阻抗约束条件：

其中，N为变电站中断路器总数，N=N1+N2+N3。无论断路器处于断开还是闭合状态，式（4）都成立。

将断路器在闭合、断开以及状态未知情况下的约束条件作为虚拟量测，可以进一步提升状态估计量测冗余度，进而提升估计精度。将节点电压相量和断路器电流相量的PMU量测值以及断路器零阻抗虚拟量测量和节点零注入电流虚拟量测量共同作为状态估计的量测量。给出各量测量的量测方程并求得雅可比矩阵，就可以利用NWLS进行求解，得到估计结果。

2.2 量测方程

状态估计中的量测量包括节点电压幅值和相角、断路器电流实部和虚部以及变电站进出线电流实部和虚部。此外，状态估计中还应考虑节点零注入电流虚拟量测和断路器的零阻抗特性虚拟量测，进一步提升量测冗余度。要利用量测量进行状态估计，需要得到量测量与状态量之间的函数关系，即量测方程。由于考虑了节点零注入电流虚拟量测，将节点分为含有进出线的非零注入节点和零注入节点2类，2类节点的个数分别为N4和N5。

对于非零注入节点，进出线电流实部和虚部量测量分别为IRinp和IIinp，规定注入节点电流为正，则IRinp和IIinp与状态量之间的函数关系为：

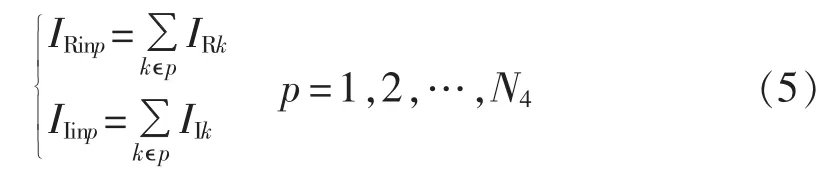
其中，IRinp和IIinp分别为含有进出线的非零注入节点的电流量测量的实部和虚部；kϵp表示断路器k与节点p相连。

对于零注入节点，虚拟量测方程为：

其中，NL为变电站中节点总数，NL=N4+N5；kϵq 表示断路器k与节点q相连。

电压幅值和相角的量测值Uzi和θzi与状态量之间的函数关系为：

断路器的电流实部和虚部的量测IRzk和IIzk与状态量之间的函数关系为：

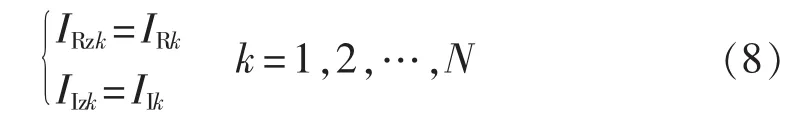
此外，量测方程还包括断路器的零阻抗特性虚拟量测。因此，式（2）—（8）共同构成了基于断路器零阻抗特性的状态估计量测方程：

其中，z为量测向量；h为非线性量测方程；x为状态向量；O 为零向量，维数为 1×（2N1+2N2+4N3+2N5）；v为量测误差，其满足均值为0、方差为σ2的正态分布。

NWLS状态估计中需要用量测误差方差矩阵的逆矩阵作为权重矩阵。因此，需要得到各量测量的量测误差方差。对于节点电压幅值和相角直接量测，误差方差就是幅值、相角PMU量测误差方差。零注入电流虚拟量测和零阻抗特性虚拟量测通常认为是绝对准确的量测，可以选取一个较小的正数作为量测误差方差。由于PMU电流相量量测量为电流幅值和相角，而状态估计中采用的是电流实部和虚部，因此，需要将极坐标下的PMU电流相量量测转化至直角坐标下，相应的量测误差方差也需要根据误差传递公式[14]进行转换。将PMU量测和虚拟量测误差方差作为对角元素形成量测误差方差矩阵R：

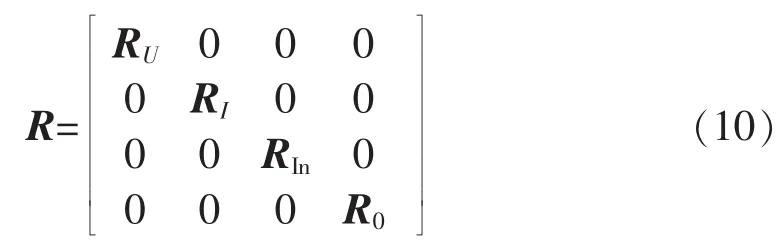
其中，RU和RI分别为节点电压和断路器电流量测误差方差阵；RIn为进出线电流量测误差方差阵；R0为虚拟量测误差方差阵。

得到量测误差方差矩阵后，对方差矩阵求逆就是NWLS量测量的权重矩阵。对量测方程关于各状态量求偏导数，就可以得到雅可比矩阵，进而就能够利用NWLS进行状态估计。

3 雅可比矩阵的计算

NWLS状态估计中需要利用量测量修正方程对状态量进行迭代修正，最终得到状态量估计值。量测量修正方程为：

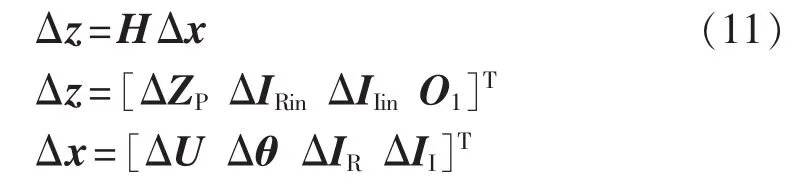
其中，H为量测方程的m×n维雅可比矩阵，m和n分别为量测量维数和状态量维数；Δz和Δx分别为量测量和状态量的修正量；ΔZP为节点电压幅值和相角以及断路器电流实部和虚部量测量修正量；ΔIRin和ΔIIin分别为进出线电流量测量修正量；ΔU、Δθ、ΔIR和ΔII分别为节点电压和支路电流相量的修正量；O1为4N3×1维零矩阵。 将式（11）展开为下列形式：

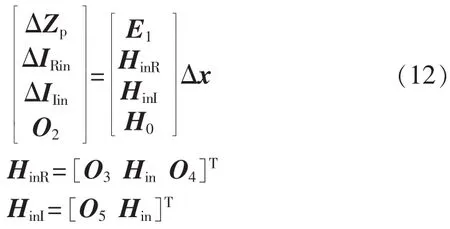
其中，E1为 2（NL+N）×1 维单位矩阵；HinR和 HinI分别为进出线电流实部和虚部量测的雅可比矩阵；O2—O5均为零矩阵，维数分别为 2（N5+N1+N2+2N3）×1、N5×2NL、N5×N、N5×（2NL+N）；H0为虚拟量测的雅可比矩阵，由零注入电流以及断路器零阻抗特性虚拟量测雅可比矩阵组成，表达式如式（13）所示。

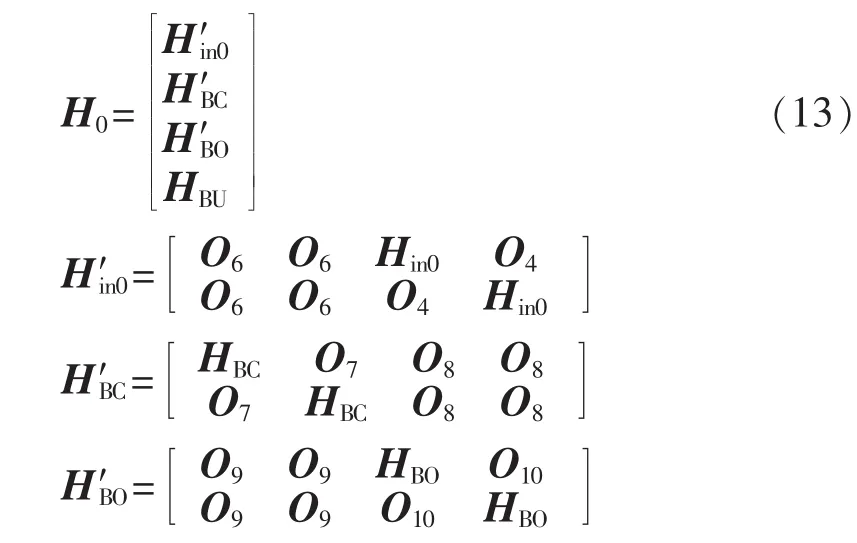
其中，Hin0为节点零注入电流实部和虚部虚拟量测雅可比矩阵；HBC、HBO和HBU分别为断路器闭合、断开和状态未知情况下虚拟量测的雅可比矩阵；O6—O10均为零矩阵，维数分别 N5× NL、N1× NL、N1× N、N2×NL、N2×N。

对于进出线电流量测量IR4和II4，式（12）中雅可比矩阵Hin的第i行第k列元素hinik取值为：

其中，i、j为断路器 k 两端的节点；i=1，2，…，N4。

对于式（6）所示的节点零注入电流实部和虚部虚拟量测，式（13）中雅可比矩阵Hin0中的第i行第k列元素hin0ik取值为：

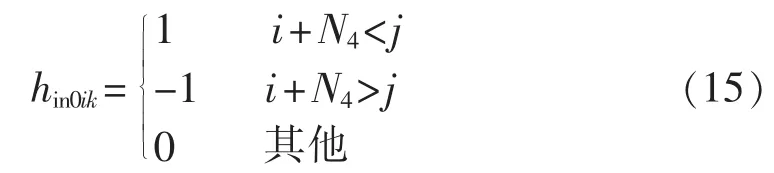
其中，i+N4表示断路器 k 的端点；i=1，2，…，N5。

对于式（2）所描述的闭合断路器零阻抗虚拟量测，式（13）中雅可比矩阵HBC的第k行第i列元素hBCki为：

其中，k=1，2，…，N1。

对于式（3）所描述的断路器断开虚拟量测，式（13）中雅可比矩阵HBO为：

其中，O11、O12分别为 N2×N1维、N2×N3维的零矩阵；E2为 N2×N2维单位矩阵。

对于式（4）所描述的断路器状态不确定情况下的虚拟量测雅可比矩阵计算，先将式（4）写为如下形式：

则式（13）中的雅可比矩阵HBU为：

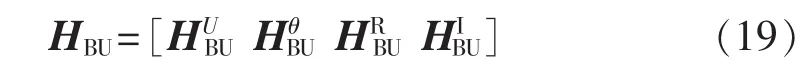
其中，HUBU和HθBU均为4N3×NL维矩阵；HRBU和HIBU均为4N3×N维矩阵。式（19）中各元素的取值如式（20）—（23）所示。

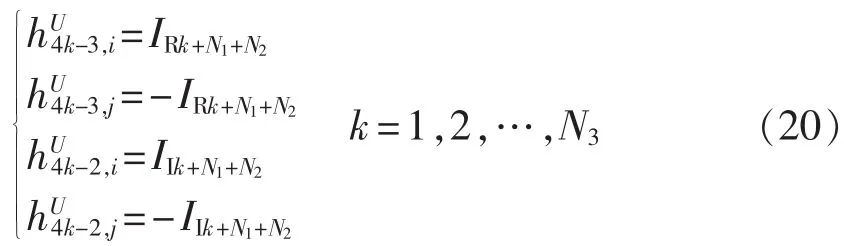
其中，i、j表示断路器k+N1+N2两端的节点。

其中，i、j表示断路器k+N1+N2两端的节点。

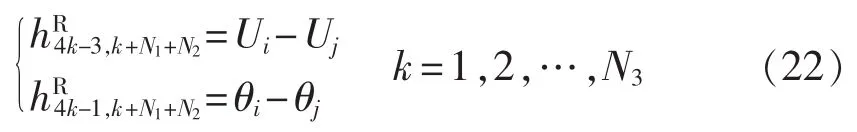
其中，i、j表示断路器k+N1+N2两端的节点。

其中，i、j表示断路器k+N1+N2两端的节点。

得到量测误差方差矩阵和雅可比矩阵后，就可以利用NWLS对状态量进行迭代计算，最终得到估计值。迭代计算公式为：

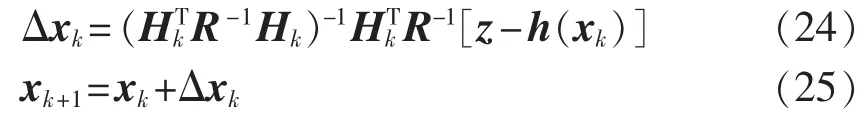
4 仿真研究

利用IEEE 39节点测试系统对所提出的状态估计方法进行仿真研究。该测试系统中节点16的具体接线形式如图3所示，图中下方的图形为虚线框内部分的放大，其中断路器左侧箭头表示流过断路器电流的正方向。利用Matpower潮流程序计算结果作为真值，在真值的基础上叠加均值为0的高斯白噪声作为量测值。根据电力系统实时动态监测系统技术规范[15]的规定，PMU相角量测误差标准差通常为0.2°，即0.0035 rad；幅值量测误差标准差为0.2%，即0.002。因此，相角和幅值所叠加的高斯白噪声标准差分别为0.0035 rad和0.002。虚拟量测的误差方差比PMU量测低一个数量级，选为10-8。断路器9的实际状态为闭合，计算过程中假设其状态不确定。

状态量估计结果见表1、2，其中电流、电压均为标幺值。可以看出，所有节点的电压幅值和相角估计值都相等，这是由于考虑了断路器的零阻抗特性。对于闭合断路器1—6，其两端节点的电压幅值和相角都相等；对于状态不确定的断路器9，则一定满足式（4）所示的虚拟量测，由于其实际状态为闭合，因此，其两端节点电压相量也必然相等。同时，流过断路器7和8的电流实部和虚部的估计结果为0，这是因为断路器为断开状态，满足式（3）所示的虚拟量测。

图3 IEEE 39节点测试系统Fig.3 IEEE 39-bus test system

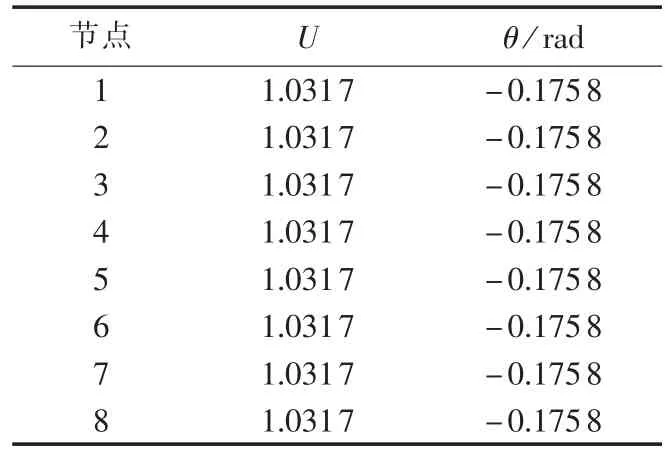
表1 节点状态量估计结果Tab.1 Results of nodes state estimation

表2 断路器状态量估计结果Tab.2 Results of breakers state estimation

此外，由估计结果可以看出，断路器9两侧节点的电压幅值和相角均相等，且电流也非零，由此可以判断断路器9的状态为闭合。

为了获取量化的估计指标，定义滤波系数η：

其中，M为量测量个数；SEi、STi和SMi分别为量测量的估计值、真值和测量值。经过300次计算取平均值，得到了较为稳定的数值0.2729。可见，本文提出的状态估计方法能够有效滤除量测量的随机误差。

进一步对算法的实时性和收敛性进行分析。通过IEEE 39节点测试系统对本文的方法进行仿真验证，单步计算时间约为0.0047 s，能够满足系统动态监控的实时性需求。由于本文提出的分布式状态估计是针对每一个变电站单独实施，因此，随着系统规模的扩大，每个变电站内基于零阻抗特性的状态估计计算速度不会发生变化。此外，非线性最小二乘的收敛条件ε设置为10-8，电压幅值和相角的初值分别设为1和0；电流相量初值均采用量测值。算法经过2次迭代就达到收敛条件。2次迭代状态量残差绝对值最大值分别为 0.1762和 3.2×10-10。可见，算法具有较强的收敛性。

5 结语

针对故障后网络拓扑结构改变，难以实时获得，传统集中式状态估计不可行的问题，提出了一种系统动态过程中基于PMU量测的分布式状态估计框架结构。充分考虑断路器的零阻抗特性约束条件，在变电站内进行状态估计，并将估计结果上送至调度中心。对于故障后状态未知的断路器，利用零阻抗特性对其构造虚拟量测方程，提升冗余度。仿真分析表明，该方法不仅具有较好的滤波效果，同时能够根据估计结果判断出状态未知的断路器的实际开合状态。算法能够满足实时性需求，并可靠收敛，具有一定的现实意义。