马科维茨模型、相对方差与出口地理集中度

蔡一鸣

（华南师范大学 经济与管理学院，广东 广州 510006）

一、前 言

二战结束以来，国际贸易发展迅速。一些国家特别是发展中国家出口地理集中度较高的问题凸显出来①出口地理集中度是衡量出口市场多元化程度的一个指标，地理集中度越高表明多元化程度越低。，并在一定程度上导致了出口收入的波动［1］。国内外相关文献主要侧重于研究出口地理集中度的衡量方法及其与出口波动之间的因果关系。国外学者衡量地理集中度的方法主要包括Hirschman指标、Ogive指标、Entropy指标、Herfindahl指标和Aggregate Specialization指标［2］。其中，Hirschman指标较为常用，Herfindahl指标和Aggregate Specialization指标等都由其衍生而来。国内学者根据各自的研究目标也构建了一些指标，如各出口市场出口份额的标准差［3］、均匀度［4］等。另外，还有一些比较简单的方法，如使用出口国最大的5个或10个出口市场的出口份额表示地理集中度［5－6］。

一般认为，地理集中度过高会导致出口收入的不稳定。这种观点已经成为各国政策制定者实施出口市场多元化战略的依据［7］。可是，在经验分析中二者的关系并不明确。Hirsch和Lev［8］270－277对丹麦、荷兰和以色列三国共500家企业的统计分析表明，地理集中度越低出口收入越稳定。Qian［9］和Sarada等人［10］分别对美国企业和印度企业的研究也支持Hirsch＆Lev的结论。国内一些学者对中国出口贸易的研究也证明二者之间存在上述因果关系［11－12］。另一方面，却有研究表明二者的关系并不显著甚至负相关［13－14］。事实上，如果出口市场的需求平稳，即使地理集中度较高也不会造成出口收入的较大波动；反之，如果各出口市场的需求波动较大且正相关程度较高，较低的地理集中度也会导致较大的出口波动。

在优化出口地理集中度方面，很多研究往往建议“开拓新市场”。但是如何开拓以及安排各出口市场的出口比例，并没有给出具有可操作性的解决途径［15］［16］。很明显，如果以稳定出口为目标，地理集中度的优化至少应考虑出口的波动风险。马科维茨［17－18］的均值—方差方法为此问题提供了一条解决思路。Hirsch和 Lev［8］270－277的研究较早将马科维茨的理论与出口市场多元化联系起来，但是仅仅验证了出口市场多元化与出口波动之间的反向关系。随后，一些学者开始尝试将此方法应用于旅游业客源国市场的最优选择。比如，Board等人［19－20］、Kennedy［21］、Jang和Chen［22］使用不同的预期“收益”变量——来自各客源国的夜床次（bednights）、旅游收入的增长率以及旅客数量，分别研究了西班牙、爱尔兰和台湾地区旅游业客源国市场的有效组合。这些研究虽然没有计算出口地理集中度（根据有效组合可以直接计算），但其研究目的本质上与后者相同。不过，Board等人和Kennedy的研究没有考虑预期“收益”变量的均值之间的显著差异，而这种差异会导致方差或标准差衡量的风险不具有可比性；而Jang和Chen的研究没有区分旅客数量的波动特点，对于不同的波动特点需要构建不同的理论模型（详见后文第四部分）。本文试图克服上述局限，为政策制定者优化出口地理集中度提供更加坚实的理论基础。

二、出口与证券投资之间的异同点

马科维茨的均值—方差方法最初主要应用于有价证券等资本市场。经过不断发展，这一方法扩展到几乎所有真实资产和金融资产的选择问题。“不确定性”和“不完全正相关性”是应用马科维茨方法的两个必要条件。资产收入的不确定性意味着存在降低风险的必要性，而资产收入之间的不完全正相关性意味着通过分散化投资可以降低风险。出口收入与证券收入类似，也存在不确定性和不完全正相关性两个特点。

投资者和出口国都面临着收入的不确定性，但是不确定性的表现形式并不相同。对于证券投资者而言，投资数量一般仅取决于投资者的购买力和购买意愿，而证券价格却受到一系列外在因素的影响，比如国际局势、新发明以及企业经营管理的失误等都能影响一种或多种证券的价格从而影响收益水平。因此，投资者收入的不确定性主要来自价格的波动。对于出口国而言，除了其供给能力和供给意愿，出口市场的国内政局、供需状况和国际局势等因素既影响出口产品的价格也影响出口数量。所以，一国出口收入的不确定性表现为出口数量和出口价格二者的波动。以中国出口（根据中国海关统计数据）为例，在2001年至2012年期间，由于出口数量和出口价格两方面的波动，对亚洲15经济体（包括东盟10国、日本、韩国、中国香港、中国台湾和中国澳门）、亚洲其他市场、欧盟、欧洲其他市场、北美、大洋洲、非洲和拉美8个地区市场的出口收入增长率存在明显的波动性，并导致中国总出口收入的增长率最高时达到35.4%，而最低时为－16%。

出口和证券投资中不确定性方面的差异，意味着投资者与出口国为了降低波动风险而选择的稳定目标可能不同。比如，投资者会选择最小化预期收益率的波动风险作为目标，而出口国则可以选择最小化预期出口量（出口数量或出口收入）或者最小化预期出口增长率的波动风险作为目标。进一步地，出口国和投资者稳定目标的不同导致方差不适合用来衡量出口所面临的波动风险。如果完全采用马科维茨的方法，以方差衡量出口波动风险并构建出口市场组合模型，存在以下三个方面的问题：第一，方差概念一般被认为不适合用于比较不同水平的数列的波动程度［23］。而一国对各出口市场的出口量或出口增长率的均值并不相同，并且往往存在显著差异①以中国在2000年至2012年期间对8个地区市场的出口为例，来自亚洲15经济体的年均出口收入为大洋洲的20.3倍，而来自拉丁美洲的出口收入的年均增长率比亚洲15经济体高出10.5个百分点。进一步地，如果考虑的出口市场为单个国家或经济体，这种差异会更加显著。。如果不同数列的均值之间存在差异，只有剔除均值的影响，才能更准确地比较不同数列之间的波动程度；第二，如果一国对各出口市场的平均出口量或平均出口增长率存在显著差异，该国在各出口市场所面临的以方差衡量的风险也往往存在显著差异，理论上可能最终导致组合市场的方差趋于上升甚至无界［24］；第三，对于既定的预期出口量（或预期出口增长率）和市场组合风险，方差越大的市场被分配的出口比例往往越小，而方差越小的出口市场被分配的出口比例往往越大。但是方差越小的出口市场其市场规模一般也较小，从而可能无法承受大规模的出口。除了不确定性外，证券投资的另一个突出特征是证券价格或收益之间存在不完全正相关性。类似地，一国对各市场的出口也往往具有一定的同步性。仍以中国出口为例，在2001年至2012年期间对上述8个地区市场的出口收入增长率之间都存在不完全正相关的关系（相关系数最大的为0.923，最小的为0.689）。

综上所述，鉴于出口与证券投资在不确定性和相关性方面所存在的相似性，理论上借鉴马科维茨的方法以降低出口中的非系统性风险具有可行性。但是，二者在不确定性方面表现形式的不同，意味着需要寻找合适的方法去衡量出口所面临的波动风险。

三、相对方差与出口波动风险

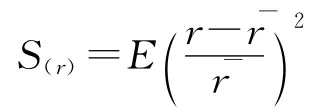
此公式度量的不再是数列中各数据相对于均值的绝对偏离的平均水平，而是相对于均值的相对偏离的平均水平。与标准差系数一样，相对方差也可用于不同性质、不同单位或具有不同水平的数列的离散程度的比较。在数值上，相对方差等于标准差系数的平方，因此避免了均值为负值时使用标准差系数衡量离散程度的复杂情况。并且，相对方差越大反映各数据之间的相对差异越大，相对方差越小则反映相对差异越小。

进一步地，根据相对方差的定义，可以得到如下推论：

根据相对方差的上述性质，同时考虑到出口国对各出口市场平均出口量或平均出口增长率之间的差异往往较大，我们认为相对方差比方差更适合衡量出口波动风险。其原因在于，一方面相对方差衡量的是出口量或出口增长率相对于均值的离散程度，消除了均值的影响，从而使各出口市场的波动风险具有可比性。另一方面，使用相对方差衡量风险将使各出口市场的风险差异程度显著降低（相对于方差衡量的风险），从而减少了理论上组合风险趋于上升甚至无界的可能性。

四、出口市场组合与最优地理集中度

一国对各出口市场出口量的波动特点，理论上大致存在三种可能：围绕均值波动、呈上升趋势和下降趋势。如果借鉴马科维茨模型的方法以降低出口中的非系统性风险，那么针对不同的波动特点应该选择不同的预期“收益”变量。比如在第一种波动中，出口国面临的是该类市场中所有出口量的不确定性，从而预期的“收益”变量可以选择为出口量，并需要构建以稳定出口量为目标的出口市场组合模型。而在第二和第三种波动中，出口国面临的只是出口增长率的不确定性，从而预期的“收益”变量可以选择为出口增长率（如果仍然选择出口量作为预期收益变量，将高估各出口市场的风险），并需要构建以稳定出口增长率为目标的出口市场组合模型。

（一）以稳定出口量为目标的出口市场组合模型

1.假设

（1）出口国对各出口市场的出口量为服从正态分布的随机变量；（2）出口量围绕均值波动；（3）出口国建立出口市场组合的原则是，在既定的出口量下使波动风险最小化。

2.模型

根据前文第三部分中的推论1，如果稳定目标为最小化预期出口量的波动风险，则目标函数及其约束条件为：

其中，Xi表示出口国对第i个市场的出口量占总出口量的份额，bi表示出口国对第i个出口市场的潜在最大出口份额。对Xi的非负限制，类似于证券投资场合对卖空的限制，即不考虑出口国作为贸易中间商的情形。MP表示出口市场的组合风险。σ2i表示出口国对第i个出口市场出口量的方差，σik表示对第i个出口市场与第k个出口市场出口量的协方差。¯Ri表示对第i个出口市场的预期出口量，Rp表示N个出口市场组合的预期出口量。

（二）以稳定出口增长率为目标的出口市场组合模型

如果考虑出口量呈上升趋势的情形（呈下降趋势的情形也可以使用本小节的模型稳定出口），出口国可以选择出口增长率作为稳定目标，并构建出口市场组合模型。该模型的假设条件如下：

（1）出口国对各出口市场出口量的增长率为服从正态分布的随机变量。

（2）出口量呈上升趋势。

（3）出口国建立出口市场组合的原则是，在既定的出口增长率下使波动风险最小化。

为了最小化预期出口增长率的波动风险，出口国的目标函数及其约束条件在形式上与以稳定出口量为目标的组合模型基本相同，但是具体含义已经发生了如下变化：

其中，Xi表示不考虑预期出口增量时出口国对第i个市场的出口份额。MP仍然表示出口市场的组合风险。σ2i表示出口国对第i个出口市场出口增长率的方差，σik表示对第i个出口市场与第k个出口市场出口增长率的协方差。¯Ri表示对第i个出口市场的预期出口增长率，Rp表示N个出口市场组合的预期出口增长率。

由于Xi没有考虑预期出口增量，因此出口国对第i个市场的出口份额需要另外计算。令A代表出口国对所有出口市场的预期出口量，B代表其中的预期出口增量，则预期出口增长率为B／（A－B）＝Rp。同时，出口国对第i个市场的预期出口量为 Xi（A－B）＋Xi¯Ri（A－B）。因此，出口国对第i个市场的出口份额为 Yi＝Xi（1＋¯ri）／（1＋Rp）。进一步地，对Xi的约束如下：

bi≥Xi（1＋¯Ri）／（1＋Rp）≥0，i＝1，2，…，N。其中，bi代表对第i个市场出口份额的潜在最大值。

根据上述两类模型，设定不同的预期出口量或预期出口增长率，可以分别求解一国三类出口市场（出口量围绕均值波动、呈上升趋势和下降趋势）的有效组合。在不同的市场组合内，出口国对各出口市场的出口比例并不相同，从而地理集中度（比如可根据Hirschman指标计算得到）也往往不相同。由于每个市场组合都意味着在给定的预期出口量或预期出口增长率下已经实现了波动风险的最小化，所以与证券投资者类似，出口国政策制定者对最优市场组合从而最优地理集中度的选择，取决于其对待风险的态度。根据政策制定者的风险偏好所对应的有效市场组合，可以分别得到三类出口市场的最优地理集中度。进一步地，也可以根据出口国在所有出口市场上的出口比例，计算总的最优地理集中度。

五、全文结论及进一步的讨论

鉴于出口与证券投资在不确定性和相关性方面所存在的相似性，理论上借鉴马科维茨模型的方法以稳定出口具有可行性。同时，由于二者在不确定性方面表现形式的不同，相对方差比方差更适合衡量出口的波动风险。以稳定出口为目标，综合考虑预期出口及其波动风险，可以从稳定出口量和稳定出口增长率两个视角构建出口市场组合模型用于分析出口市场的多元化问题。根据出口市场组合模型，可以发现一国出口市场的有效组合。在此过程中，可以得到对应于不同预期出口量或预期出口增长率且已经实现风险最小化的地理集中度。而出口国对最优地理集中度的选择，取决于政策制定者对待风险的态度。

在现实中，出口市场组合模型可以为企业、行业乃至整个国家优化出口地理集中度提供理论指导。对于一个国家而言，在使用出口市场组合模型引导出口活动的过程中，应该提供相应的支持政策鼓励出口企业转换市场，当然，这个转换过程不会如证券投资者改变证券组合那样容易，甚至可能是一个中长期的过程。另外，如果出口国与有效组合中的某进口国发生贸易摩擦，则意味着对该国的出口比例可能无法实现。但是，理论上仍然可以找到另一组出口市场替代该国，从而不影响预期出口目标下的风险最小化。

［1］UNDP.Towards Human Resilience：Sustaining MDG Progress in an Age of Economic Uncertainty［J／OL］.Report of Bureau for Development Policy，2011：25.

［2］Samen，S.A Primer on Export Diversification：Key Concepts，Theoretical Underpinnings and Empirical Evidence［J／OL］.Growth and Crisis Unit World Bank Institute working papers，2010：16－17.

［3］方堃.中国外经贸市场多元化状况的计量分析［J］.国际经贸探索，2001（2）：7－11.

［4］魏浩，马野青.中国出口商品的地区结构分析［J］.世界经济，2006（5）：22－31.

［5］程国强.中国农产品出口：增长、结构与贡献［J］.管理世界，2004（11）：85－95.

［6］杨长湧.我国出口市场多元化战略的现状、影响及对策［J］.宏观经济研究，2010（6）：12－18.

［7］Adams，F.G.and Behrman，J.R.Commodity Exports and Economic Development［J］.Econometric Studies，1982（28）：23－45.

［8］Hirsch，S.，Lev，B.Stabilization Through Export Diversification［J］.The Review of Economics and Statistics，1971，53（3）.

［9］Qian，G.Assessing Product－Market Diversification of U.S.Firms［J］.Strategic Management Journal，1997（21）：155－174.

［10］Sarada，C.，Ravisankar，T.，Krishnan，M.，Anandanarayan，C.Indian Seafood Exports：Issues of Instability，Commodity Concentration and Geographical Spread ［J］.Indian Journal of Agricultural Economics，2006，61（2）：238－252.

［11］刘靖，毛学峰，辛贤.我国农产品出口不稳定性成因的初步探析［J］.中国农村观察，2006（1）：2－10.

［12］徐颖君.中国出口贸易能稳定增长吗［J］.世界经济研究，2006（8）：36－43.

［13］Massell，B.F.Export concentration and export earnings：a cross－section analysis ［J］.American Economic Review，1964，54（2）：47－63.

［14］MasselL，B.F.Export instability and economic structure［J］.American Economic Review，1970，60（4）：618－630.

［15］Love，J.Export instability in less developed countries：consequences and causes［J］.Journal of EconomicStudies，1987（14）：3－80.

［16］Piya，S.，Kiminami and A.，Yagi，H.Evaluating the Impact of Geographic Concentration on Nepalese Agricultural Export ［J］.South Asia Economic Journal，2010，11（2）：207－222.

［17］Markowitz，H.M.Portfolio selection［J］.The Journal of Finance，1952，7（1）：77－91.

［18］Markowitz，H.M.Portfolio selection：efficient diversification of investments［M］.Wiley Press，1959：26.

［19］Board，J.，Sinclair，T.and Sutcliffe，C.A portfolio approach to regional tourism［J］.Built Environment，1987，13（2）：124－137.

［20］Board，J.and Sutcliffe，C.Risk and income tradeoffs in regional policy：A portfolio theoretic approach［J］.Journal of Regional Science，1991，31（2）：191－210.

［21］Kennedy，V.Risk management in the Irish tourism industry：the contribution of aportfolio investment approach ［J］.Tourism Management，1998（2）：119－126.

［22］Jang，S.and Chen，M－H.Financial portfolio approach to optimal tourist market mixes ［J］.Tourism Management，2008（29）：761－770.

［23］贾军平，何晓群，金勇进.统计学［M］.北京：中国人民大学出版社，2000：80.

［24］马科维茨.资产选择——投资的有效分散化［M］.刘军霞，张一驰，译.北京：首都经济贸易大学出版社，2000：126－128.

［25］蔡一鸣.几种方差概念的比较［J］.统计与信息论坛，2008（4）：20－22.