叉-杆传动在阀门操作中的应用
2014-09-20
(天津冶金职业技术学院,天津 300400)
一、概述
对于传动装置而言,一般讲在电机直接驱动的情况下,其电机的转数及输出都受到一定的限制。输出功率较大的电动装置多以回转电动装置与二级减速器的组合型式进行。通常,大传动比传动的二级减速器常采用蜗轮-蜗杆传动方式。虽然蜗轮-蜗杆传动具有传动比大和工作平稳等特点,但输出扭矩的损失较多。由蜗轮和蜗杆作为驱动减速装置,如阀门(球阀、蝶阀等)的驱动装置,其扭矩特性不好。如果采用齿轮机构实现大传动比,则传动装置势必体积大而且传动效率低。如采用本文所述的叉-杆机构作为驱动减速装置实现大阀门的启闭则可以解决以上问题。
二、叉-杆装置的结构
实现直线移动和旋转运动转换的是杆和拨叉。叉-杆传动机构主要由拨叉、输出轴、限位螺钉、运动滚轮组成(见图1)。拨叉用键固定在输出轴上;传动轴(作为叉-杆传动的主动侧)安装在气缸活塞杆的端部。传动轴随气缸拉杆的伸缩而上下移动;滚轮(安装在传动轴上)在拨叉内移动迫使拨叉摆动。气缸及导向杆两端固定在箱体上。
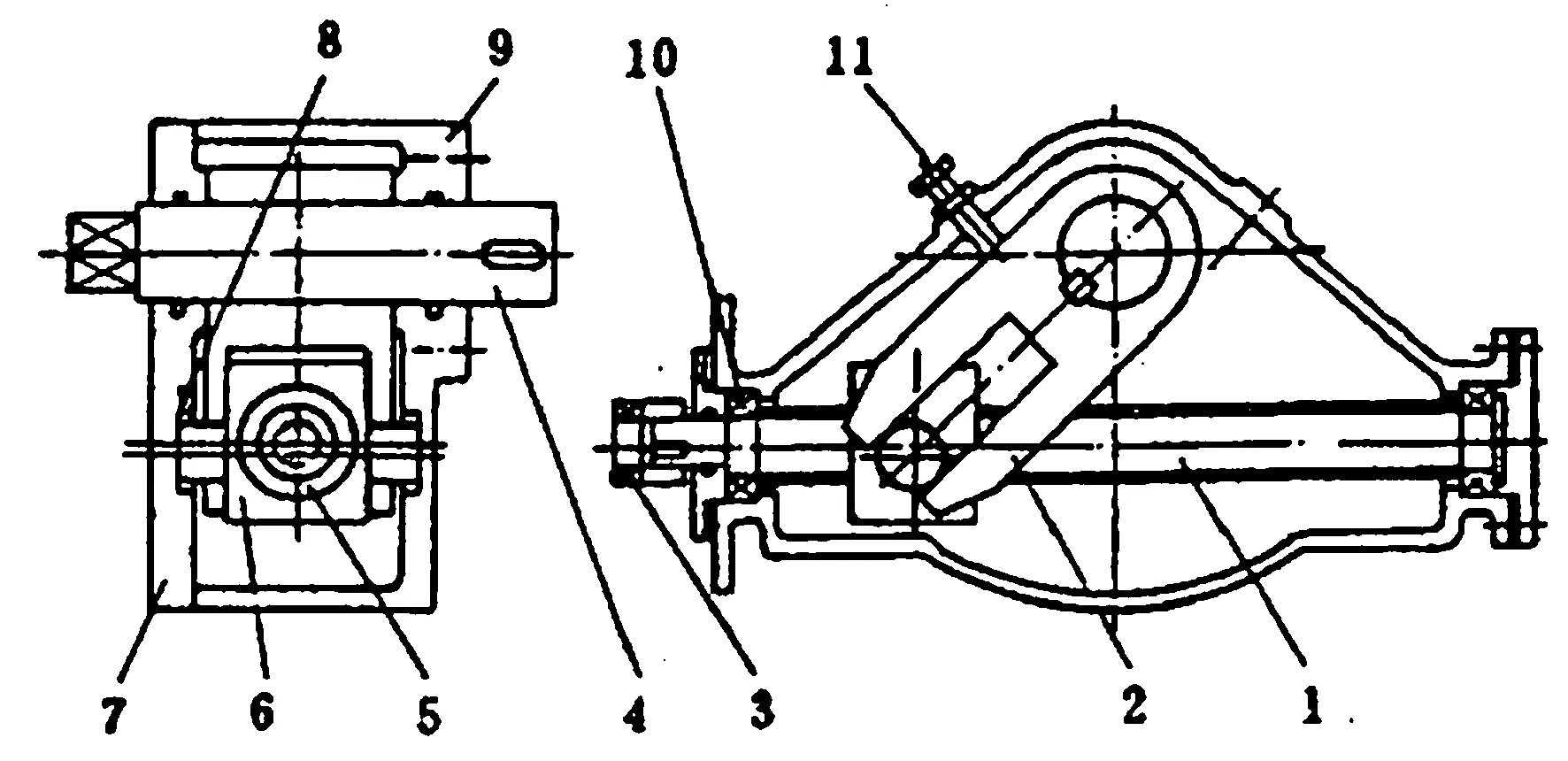
图1 叉-杆结构
当气缸进、排气时,传动轴在活塞的推拉下做上下移动并带动安装在传动轴上的滚轮在拨叉内移动,使拨叉摆动。拨叉的回转摆动驱动机构 —— 阀门启闭件(球体或蝶板)实现启闭动作。拨叉上设有可调式螺杆机构作机械限位用。
三、特点
1.叉-杆型传动机构的扭矩特性较好。其双滚轮导向结构能有效地在拨叉内移动,并能承受拨叉摆动中产生的径向力,降低了磨损,提高了传动精度,延长了部件的使用寿命。
2.传动轴与滚轮采用分体式结构,成本低,维修方便。气缸及导向套筒采用双支座支撑刚性好,移动平稳。
3.与蜗轮-蜗杆传动比较,叉-杆型减速器传动效率高,结构简单,制造成本和维修成本低。
4.可操作性高,操作灵活;由于滚轮移动范围小且灵活,不会产生卡死现象。
5.可控性高,可实现任意位置的操纵。应用于阀门启闭时可根据要求实现阀门的开启。
四、计算

图2 拨叉
1.输出力矩的计算(参见图2)
M= ηQL/cos2α —— (1)
式中
M - 输出轴的输出力矩
η- 传动效率
Q - 气缸活塞杆作用于传动轴上的轴向力
α- 输出角行程
L - 拨叉与传动轴中心距
2. 气缸推拉力的计算
设计时,应使输出预定的角行程与所需的气缸行程相匹配,以确保阀门的开度指示与实际输出的角行程相符合。下面的计算以阀门的开启和关闭为例:
气缸推力
P1=ηF*A1 —— (2)
气缸拉力
P2=ηF*A2 —— (3)
公式中:
P1-气缸产生的推力,P2 -气缸产生的拉力,η - 传动效率,F - 气体压强,A1 - 气缸内活塞面积,A2 =1/2 Л (R2- r2),R- 活塞半径,r - 活塞杆半径,活塞的行程:
S=L*tg-1α—— (4)
2S- 气缸活塞行程,α- 输出角行程,L - 拨叉与传动轴中心距。
为保证活塞运行平稳,气体回路上安装有阻尼装置,在此不作详述。从上面的公式中可以看出,影响拨叉摆动的因素为L 、P 及α , 设计时应综合考虑; L 越大,拨叉转动所需驱动力越小。但不宜取值过大,否则.对活塞杆作用的附加力矩将影响其刚性。
五、扭矩特性
从上述公式可以看出,其传动轴受到的轴向推力Q 及拨叉与传动轴之中心距L 为定值,而减速器的输出角行程α为变量。在拨叉回转过程中,其值在 -45 - +45°之间变化。因此,在输出扭矩一定的情况下,拨叉回转全过程中所需的推拉力,即拨叉的扭力也随着角行程的变化而变化。如拨叉结构图2(b)所示, 当导向滑槽的对称中心线与拨叉及传动轴的中心连线重合,其拨-叉扭矩特性如图3所示,在角行程为 45°和 -45°时输出轴扭矩最大且相等。角行程中点的扭矩最小。
对于有特殊要求的装置,如球阀和强制密封蝶阀的最大扭矩值出现在关闭终了和开启初始,即角行程等于0°的瞬间。因为在关闭终了的瞬间密封副间将产生强制密封力矩,以保证可靠的密封性。而在开启初始的瞬间,除需要克服密封副间的摩擦力矩外,还需克服密封副间的粘滞力矩。
为了使叉-杆传动具有适应于球阀和蝶阀的输出扭矩,将拨叉导向槽的对称中心线绕传动轴中心相对于拨叉输出轴与传动轴两中心连续顺时针方向旋转角度θ(见图4),此时的关闭终了(开启初始)瞬间的输出轴扭矩

图3 输出轴扭矩特性
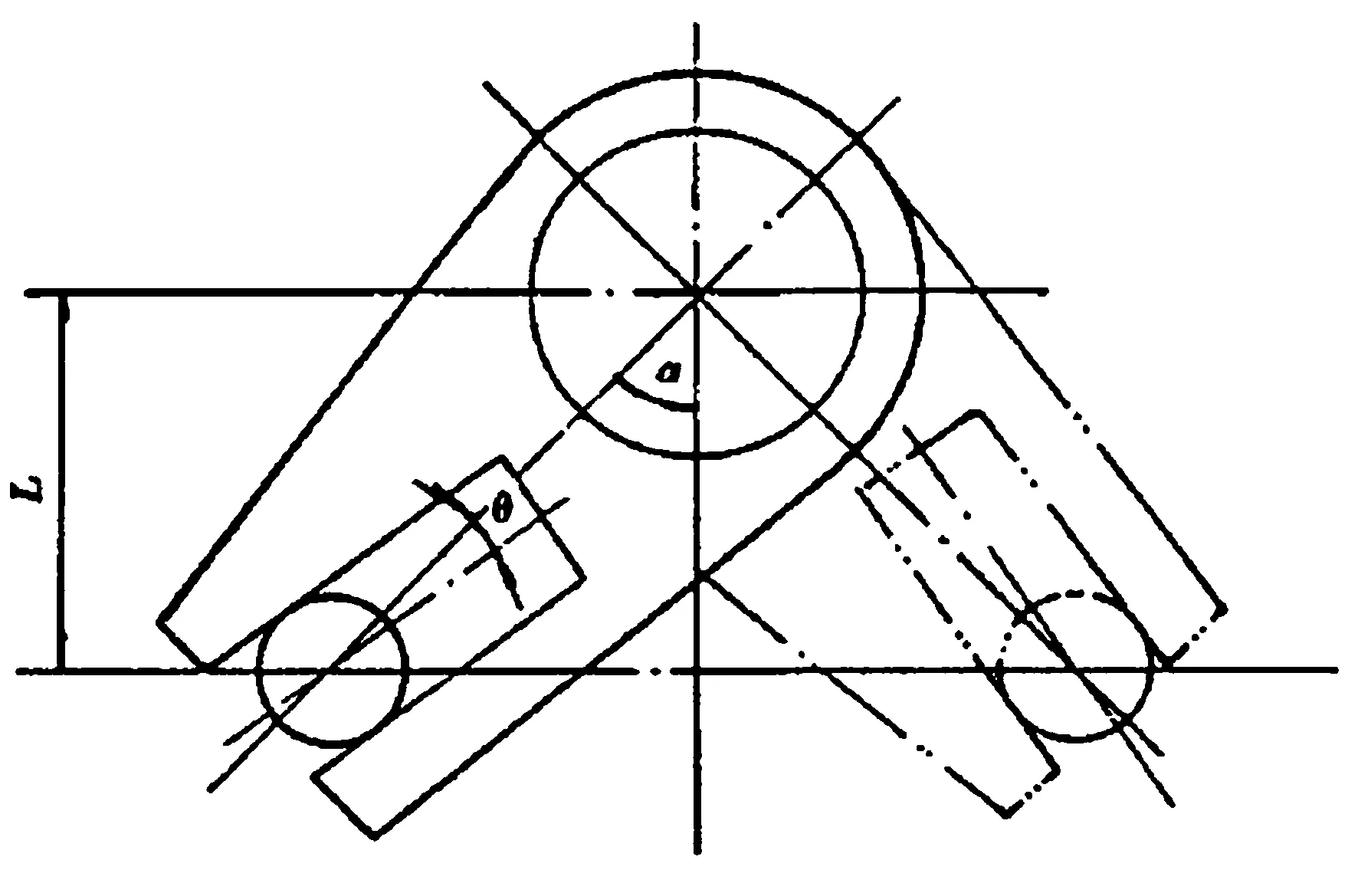
图4 拨叉顺时针旋转
Mc =ηQLcosθ/cos (α+ θ) cosα ——(5)
而开启终了(关闭初始)瞬间的输出轴扭矩
Mo= ηQLcosO/cos(α -θ) cosα——(6)
显然, Mc/ Mo >l 即 Mc > Mo
一般θ取8° -10°较为合适,其扭矩特性见图3。
六、结语
叉-杆传动减速器具有结构紧凑,传动效率高,扭矩特性好等特点,是密闭型球阀和蝶阀的理想驱动装置。
参考文献:
[1]郭仁生.机械设计基础[M].北京:清华大学出版社,2005.
[2]张秉荣.工程力学[M].北京:机械工业出版社,2007.
[3]徐锦康.机械原理[M].北京:机械工业出版社,2011.
