GOCE引力梯度数据滤波方法的设计与结果分析*

杨洪国 黄 强

1)青岛农业大学，青岛 266109

2)西南交通大学地球科学与环境工程学院，成都 610097

GOCE引力梯度数据滤波方法的设计与结果分析*

杨洪国1)黄 强2)

1)青岛农业大学，青岛 266109

2)西南交通大学地球科学与环境工程学院，成都 610097

为了滤掉GOCE引力梯度数据的低频误差，基于引力梯度数据的频谱特性设计了3种滤波方法，并选取其中滤波效果最优的一种方法处理了2009-11-02～2010-01-10共70 d的引力梯度数据。利用滤波后的70 d引力梯度数据恢复的1个200阶次的重力场模型结果显示，引力梯度数据恢复的模型必须进行正则化处理，施加了正则化的模型与GO_CONS_GCF_2_TIM_R3在160阶前具有一致的精度。

GOCE;引力梯度;低频误差;快速傅里叶变换;带通滤波器

GOCE卫星的目的是恢复高精度静态地球重力场模型。ESA预期可恢复大地水准面精度为1 cm、重力异常精度为10－5ms－2、空间分辨率为100 km(半波长)的地球重力场模型［1－3］。由于GOCE卫星自身的技术特性，导致6个梯度分量中的4个(Vxx，Vyy，Vzz，Vxz)精度较高，另外两个(Vxy，Vyz)精度较差［4］。此外，引力梯度分量含有巨大的低频误差，低频误差的滤波处理直接影响到恢复重力场模型的计算。目前，ESA已发布了大量的引力梯度数据，包括两种数据产品:EGG_TRF_2_和EGG_NOM_2_。其中，EGG_TRF_2_为经过高通滤波处理、在局部指北坐标系LNOF(local north oriented frame)下的引力梯度数据;EGG_NOM_2_为未经滤波处理，在梯度仪坐标系GRF(gradiometer reference frame)下的引力梯度数据。由于EGG_TRF_2_在处理时引入了大量的外部模型信息，并在坐标系之间进行了转换，受到姿态误差的影响，不能用于恢复重力场模型。EGG_NOM_2_可用于恢复重力场模型的计算，但必须进行滤波处理。本文主要对引力梯度数据的噪声特性和滤波处理方法进行研究。

1 滤波方法的设计

为了避免引力梯度数据滤波后失真，将滤波对象定为观测值减去模拟值的剩余部分OMC(observation minus computation)。模拟引力梯度数据所用的模型为EGM2008的前300阶次，模拟引力梯度数据的Laplace算子的绝对值达到了10－21数量级。以2009-11-02的引力梯度数据为例，4个精度较高的梯度分量的OMC时间序列见图1。

根据引力梯度数据的频谱特性，本文设计了3种引力梯度数据滤波方法。

方法1:利用FFT技术把时域下的引力梯度数据转换到频域，将频带外的各频率点赋0值，观测频带为5 mHz～0.1 Hz，并利用FFT技术将频域下的序列值转换到时域。

方法2:直接采用FIR(finite impulse response)滤波器对引力梯度序列进行处理。带通滤波器的阶数设定为1 000阶，通带设定为5 mHz～0.1 Hz，窗函数为汉宁窗。为了避免滤波结果出现相位漂移现象，将引力梯度序列分别按正向和反向通过FIR滤波器，即

式中，h(n)为带通滤波器，x0(n)为原始梯度数据序列，x1(n)为正向滤波后的梯度序列，x2(n)为反向的梯度数据序列，x3(n)为反向滤波后的梯度数据序列，x4(n)为经过正反向滤波后的梯度数据序列。

方法3:在傅里叶多项式的基础上，以每个频率点处的相位值作为未知参数，建立引力梯度观测值关于各频率点相位的观测方程，利用最小二乘法解算出各频率点的相位值，然后利用各频点的相位值计算出各历元的低频误差，在观测值中扣除各历元的低频误差。利用带通滤波器或低通滤波器处理高频误差，即

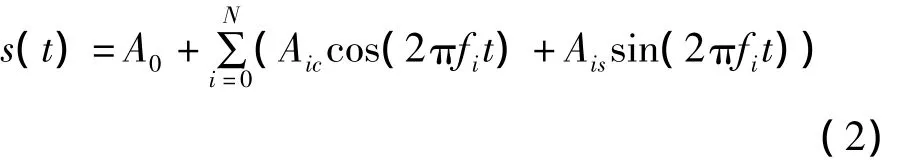
图1 OMC的时间序列Fig.1 The time series of OMC data

式中，s(t)为时刻 t处的引力梯度值，A0、Aic和 Ais为傅里叶多项式的系数，fi为第i点的频率，fi的最大值为低频带的上限0.005 Hz。利用式(2)通过最小二乘法即可得到低频误差。

2 数据计算与分析

利用3种滤波方法对2009-11-02～2010-01-10的引力梯度数据进行滤波处理，方法1滤波后的功率谱密度见图2。

图2 方法1滤波后的结果Fig.2 The filtered results with method 1

从图2可见，引力梯度在频带(5 mHz～0.1 Hz)内的信号被提取出来，频带外的梯度信号被全部去掉。由于频带外的信号为0，在FFT逆变换时出现了混频现象，并导致频带内梯度信号的谱密度降低。这种滤波方法降低了引力梯度在频带内的精度，最终将影响重力场模型的恢复。

方法2滤波后的功率谱密度见图3。从图3可见，FIR带通滤波器能够完整地提取出频带内的梯度信号，并且保留频带外的引力梯度信号，滤波效果较好。

方法3滤波后的功率谱密度见图4。图4中，OMCxx0、OMCyy0、OMCzz0 和 OMCxz0 为减去低频误差 后 的 结 果;OMCxx1、OMCyy1、OMCzz1 和OMCxz1为最终的滤波结果。可见，滤波后的结果能较好地提取出观测频带内的信号。

在引力梯度张量中，Laplace算子是评价引力梯度质量的重要指标。为了更好地评估3种方法，计算了3种方法滤波后梯度的Laplace算子的绝对值(表1)。从表1可见，方法1的平均值和标准差都为最小，但是个别值的精度极差，大于100×10－12s－2，远低于梯度测量仪在频带内的精度。由此可见，方法1出现的混频现象使滤波后的引力梯度数据失真。方法2和方法3滤波后的结果精度接近，但总体上看，方法3的精度最高。从实测的引力梯度数据的滤波结果可知，实测的引力梯度数据精度略低于标称精度［5］。

表1 3种滤波结果的统计(单位:10－12s－2)Tab.1 Statistics of the results from three filtered methods(unit:10 －12s－2)

图3 方法2滤波后的结果Fig.3 The filtered results with method 2

采用第3种方法对2009-11-02～2010-01-10共70 d的引力梯度数据进行滤波，并以滤波后的引力梯度数据为基础利用时域法恢复200阶次的地球重力场模型(参与计算的数据包括精度较高的4个分量，精度较差的两个分量不参与反演计算)。由于GOCE卫星的太阳同步轨道特性，导致观测数据无法完全覆盖地球，在地球两极分别有半径约为6.5°的空白区域［6－7］。两极空白将会导致法方程严重病态，解算的模型的带谐位系数附近会形成一个严重的低精度带(图5(a))。为了抑制法方程的病态，对法方程进行Kaula正则化，最优正则化参数α=10－12.3，选取的原则是以反演模型的大地水准面误差最小为标准。施加了Kaula正则化后恢复的模型能有效体现出引力梯度数据在中短波信息方面的优势(图5(b))。

从图5(a)可见，无正则化的模型在带谐位系数附近误差很大，而施加了Kaula正则化之后带谐位系数精度得到了明显改善(图5(b))，但个别低阶次位系数精度仍然偏低。从梯度数据反演的模型可见，梯度数据的优势在重力场模型的高阶次部分。

图4 方法3的滤波结果Fig.4 The filtered results with method 3

为了比较恢复的重力场模型精度，计算了3个模型的阶方差，包括利用70 d梯度数据无正则化反演的模型Model1，利用70 d梯度数据施加Kaula正则化反演的模型Model2，ICGEM公布的利用近18个月的GOCE观测数据反演的模型GO_CONS_GCF_2_TIM_R3，用Model3表示。阶方差比较见图6。

图5 无正则化和Kaula正则化恢复的模型Fig.5 Gravity field model without regularization and with Kaula regularization

图6 3个模型的阶方差比较Fig.6 Comparison of degreevariance of three models

从图6可见，无正则化的模型Model1不可用;施加了Kaula正则化的模型Model2在160阶以前与Model3具有相同的精度，在160阶以后，Model2的精度低于Model3。在160阶以后精度略低的原因可能是恢复 Model2仅用了70 d数据，而恢复Model3用了近18个月的数据。从恢复的模型可知，本文所用的引力梯度数据能有效地滤掉低频误差，滤波后的引力梯度数据能满足恢复重力场模型的需要。

3 结论

1)从3种滤波方法的滤波结果可知，GOCE实测引力梯度数据的精度并未达到发射前设计的标称精度3.2×10－12s－2，略低于 ESA 的标称精度。由于低频误差的量级较大，未经滤波的梯度数据不能用于恢复重力场模型。

2)利用滤波方法3处理的70 d引力梯度数据恢复了1个200阶次的重力场模型，施加正则化后能体现出GOCE引力梯度数据在中短波方面的优势。施加了正则化的模型在160阶以前与ICGEM公布的GOCE时域法模型精度一致;160阶以后本文恢复的模型精度略低，原因可能是本文参与计算的数据量较少。

3)从恢复的模型可见，本文所采用的引力梯度数据滤波方法可用于恢复地球重力场模型。GOCE卫星的远期目标是恢复高精度的静态重力场模型，本文的工作为进一步联合GOCE轨道和引力梯度数据恢复高精度重力场模型作好了准备。

1 Pail R，et al.First GOCE gravity field models derived by three different approaches［J］.Journal of Geodesy，2011，85(11):819－843.

2 万晓云，于锦海，曾艳艳.GOCE引力梯度的频谱分析及滤波［J］.地球物理学报，2012，55(9):2 909 －2 916.(Wan Xiaoyun，Yu Jinhai，Zeng Yanyan.Frequency analysis and filtering processing of gravity gradients data from GOCE［J］.Chinese J Geophys，2012，55(9):2 909 －2 916)

3 Floberghagen R，et al.Mission design，operation and exploitation of the gravity field and steady-state ocean circulation explorer mission［J］.Journal of Geodesy，2011，85(11):749 －758.

4 徐新禹，等.GOCE卫星重力梯度测量误差分析及其模拟研究［J］.大地测量与地球动力学，2010(2):71 －75.(Xu Xinyu，et al.Research on analysis and simulation of gravity gradiometry error of GOCE satellite［J］.Journal of Geodesy and Geodynamic，2010(2):71 －75)

5 钟波.基于GOCE卫星重力测量技术确定地球重力场的研究［D］.武汉:武汉大学，2010.(Zhong Bo.Determination of earth’s gravitational field based on the GOCE gravity measurement technigue［D］.Wuhan:Wuhan Univercity，2010)

6 Metzler B，Pail R.GOCE data processing:the spherical cap regularization approach［J］.Studia Geophysica et Geodaetica，2005(4):441 －462.

7 Ditmar P，Kusche J，Klees R.Computation of spherical harmonic coefficients from gravity gradiometry data to be acquired by the GOCE satellite:regularization issues［J］.Journal of Geodesy，2003，77(7 －8):465－477.

DESIGN OF FILTERING METHOD OF GOCE GRAVITY GRADIENT AND ANALYSIS OF RESULT

Yang Hongguo1)and Huang Qiang2)
1)Qingdao Agriculture University，Qingdao 266109
2)Faculty of Geoscience and Environment Engineering，Southwest Jiaotong University，Chengdu610097

For the reason that GOCE gravity gradients is impacted badly by low frequency error，three filtered methods were designed based on the spectral characteristics of GOCE gravity gradients.The best method was choosed through comparison of the results with the three methods.The method was applied to filter 70 days gravity gradients between 2009-11-02—2010-01-10.An Earth’s gravity field model with 200 degree and order was reconstructed based on 70 days filtered gravity gradients.The results show that reconstruction of model have to be processed with regularization.The precision of the regularized model is consistant with that of GO_CONS_GCF_2_TIM_R3 with 160 degrees.The results prove that the designed method can filter gravity gradients successfully.

GOCE;gravity gradients;low frequency error;fast Fourier transform;band pass filter

P223.0

A

1671-5942(2014)03-0146-05

2013-08-23

中央高校基本科研业务费专项(20120184120006)。

杨洪国，男，1976年生，工程师，主要从事大地测量学与测量工程研究。E－mail:874143839@.qq.com。