一种基于向量的空间圆检测方法*

赵鹏飞

(上海市测绘院，上海 200063)

一种基于向量的空间圆检测方法*

赵鹏飞

(上海市测绘院，上海 200063)

提出一种新的空间圆检测方法。首先以观测点拟合平面，然后采用空间向量构成中垂面的方法拟合球壳，并加入圆心在拟合平面内的限制条件，直接解算空间圆的圆心坐标及半径;同时在拟合过程中加入粗差剔除。该方法的数学模型可靠、拟合精度高，相比其他拟合方法，其实现更加简便。

空间圆检测;平面拟合;中垂面;球壳拟合;粗差剔除

在工程实践中，经常会遇到空间圆形物体的检测，例如地铁工程中的洞门检测、隧道断面检测、收敛测量等，都可以归纳成空间圆的检测问题。空间圆检测的目的是精确获得空间圆的圆心三维坐标和空间圆的半径。

一般来说，数据采集多使用高精度全站仪，以免棱镜模式获得空间圆特征点的三维坐标，通过对测量点拟合来确定空间圆的参数。目前拟合方法主要有以下3种:

方法一［1］，直接把空间圆看成平面圆进行拟合。这种方法存在较为明显的缺陷，即很难保证特征点的采集是完全在一个平面上。所以，这种方法只是一种近似的拟合，适用于要求不是特别高的空间圆检测。

方法二［2－4］，首先对观测数据进行平面拟合，将观测点投影到拟合平面上;然后采用坐标转换方式，将三维坐标转换到平面内，在平面内进行平面圆的拟合，得到圆心和半径;最后将平面圆的圆心经过坐标反算转换到原坐标系中，得到空间圆的圆心。这种方法是目前使用最多也是较为成熟的一种方法，但其拟合过程复杂，实现起来也较繁琐。

方法三［5－6］，分别拟合空间平面和球壳。球壳的拟合采用球体的标准二次方程的形式，用空间平面和球壳相交的方法确定空间圆。文献［5］与［6］存在微小差异，文献［6］增加了限制条件，即满足球心在拟合平面上，其数学模型更为严密。

本文对空间圆的表达方式类似方法三，即以空间球壳和空间平面相交来表达一个空间圆。在拟合空间球壳的过程中采用空间向量构成中垂面，通过中垂面求解球壳参数，再加入平面限制条件，最终精确求解空间圆的参数。为方便起见，将此方法称为方法四。

1 空间平面的拟合

空间圆上的观测点为 Pi，其坐标为(xi、yi、zi)，i=1，2，3，…，n。空间平面的方程一般表达式为［7］:

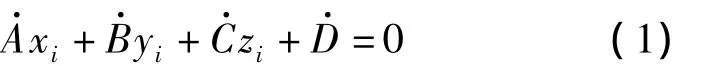
观测点Pi到拟合平面的距离为di，称为点面距:

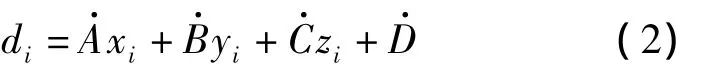
平面度体现了平面的平整程度与平面拟合的质量。拟合平面的平面度可表示为:

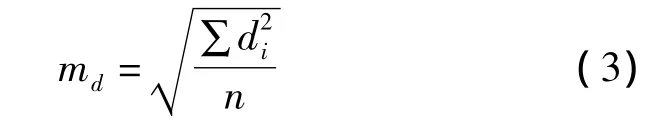
在平面拟合时，可以根据点面距的大小剔除粗差。若某观测点的残差大于限差，则视该观测量为粗差。限差可设定为2md或3md，或某个具体的数值。剔除粗差后重新解算参数，从而获取最佳拟合平面。

2 球壳拟合的限制条件

可将观测数据分别拟合成一个平面和一个空间球壳，用平面和空间球壳相交表示空间圆。但是拟合平面唯一，而拟合球壳有无穷多个。为使球壳唯一，可对其进行限制。文献［6］提出将其限制为该球壳的球心位于该拟合平面上，本文亦沿用该思路。如此，则观测点沿平面法线方向的扰动在空间圆径向方向的方向余弦为0，即平面拟合的误差对球壳拟合没有影响，也避免了所有观测点均在同一平面而造成无数组解的特殊情况。

3 空间圆的拟合

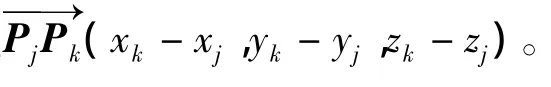
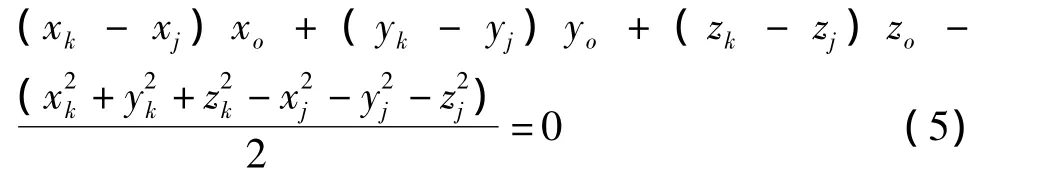
球壳的拟合需加入球心位于拟合平面的条件约束，即公式(1)写成约束方程的标准形式:

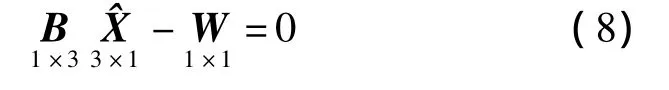
在此方法中，球壳的半径即为空间圆的半径，球壳的球心坐标即空间圆的圆心坐标。球的半径是球面上各个点到球心的距离的最或然值，即平均值。解出球心坐标后，反算各观测点到球心的距离为:

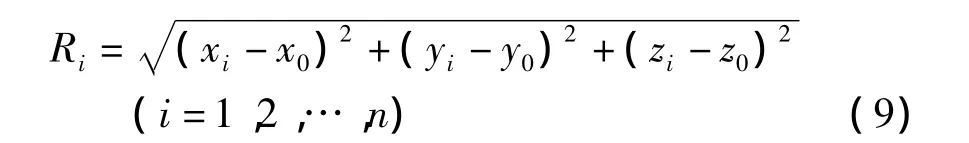
则球的半径为:

观测点到拟合球壳的距离为vi=Ri－R，称为点球距。而此时点球距等价于空间圆的点圆距，所以空间圆的圆度可表示为:

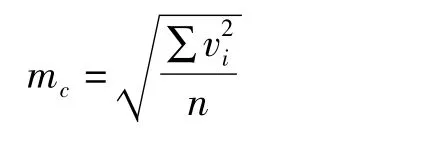
同样，可以根据点圆距的大小剔除粗差。若某观测点的点圆距大于限差，则视该观测点为粗差。限差可设定为2mc或3mc，或某个具体的数值。剔除粗差后重新解算参数，从而获取最佳拟合球壳。

4 工程算例

为了验证本文方法的正确性，以文献［4］的数据为例对其进行验证(表1)。采用方法二、方法三、方法四3种方法分别对数据进行拟合计算，结果见表2。

表1 观测点三维坐标(单位:m)Tab.1 3D coordinates of observed points(unit:m)

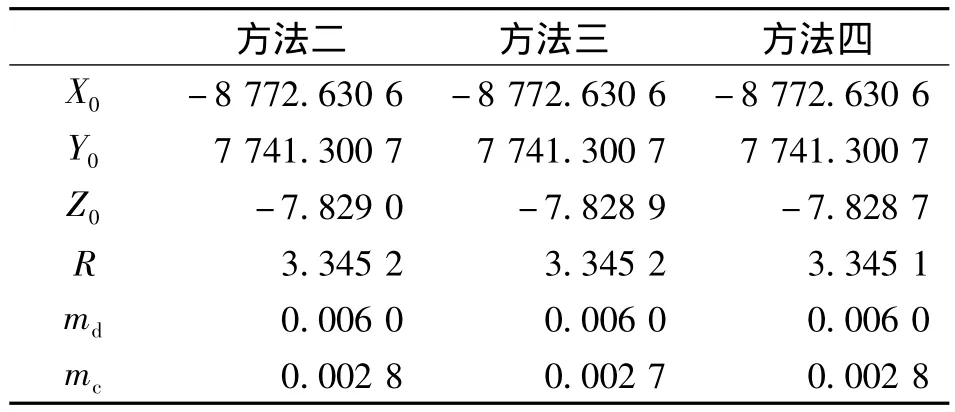
表2 3种方法的拟合结果(单位:m)Tab.2 Results fitted with the three methods(unit:m)

采用上述几种方法进行数据处理，得到几乎完全一致的计算结果，参数互差均在1 mm以内，可认为这几种方法完全等效。而方法四相比其他方法具有明显的优势:数学模型简便，便于电算程序实现，可直接获得空间圆参数，而且计算过程无需给定初值，无需繁琐的拟合计算。

5 结论

本文提出一种平面与球壳相交，球壳拟合基于中垂面的空间圆检测方法。其实现简单，是一种行之有效的方法。在实际工作中，空间圆的检测还需要注意以下几点:

1)数据的采集应尽量均匀地分布在整个空间圆的圆周上，避免拟合时产生病态矩阵。

2)粗差剔除应根据实际情况设置限差。笔者在长期隧道洞门检测工作中总结的粗差剔除经验如下:首先，在平面拟合中，将 di＞3md或 di＞1.5 cm的测量点作为粗差进行剔除，直到满足条件;然后，在空间圆拟合中，将vi＞2mc或vi＞1 cm作为粗差点进行删除，直至所有观测点满足条件，最终解算出空间圆的参数。

1 高俊强，陶建岳.利用免棱镜全站仪进行地铁遂道断面测量与计算［J］.北京:测绘通报.2005(10):41 －43.(Gao Junqiang，Tao Jianyue.Profile survey and computation of the subway tunnel using total-station instrument without prism［J］.Bulletin of Surveying and Mapping，2005(10):41 －43)

2 潘国荣，谷川，施贵刚.空间圆形物体检测方法与数据处理［J］.大地测量与地球动力学，2007(3):28－30.(Pan Guorong，Gu Chuan，Shi Guigang.The methods and data processing for 3D circular object［J］.Journal of Geodesy and Geodynamics，2007(3):28 －30)

3 王解先，赵向阳.圆形轨道变形测量［J］.工程勘察，2003(4):60 － 64.(Wang Jiexian，Zhao Xiangyang.Deformation surveying of circular orbit［J］.Geotechnical Investigation and Surveying，2003(4):60 －64)

4 赵鹏飞，雷婉南.隧道洞门安装检测新方法［J］.工程勘察，2012(3):76 －78.(Zhao Pengfei，Lei Wannan.The new test method for installation and inspection of tunnel portal［J］.Geotechnical Investigation and Surveying，2012(3):76－78)

5 潘国荣，陈晓龙.空间圆形物体数据拟合新方法［J］.大地测量与地球动力学，2008，28(2):92 －94.(Pan Guorong，Chen Xiaolong.A new method for 3D circular object fitting［J］.Journal of Geodesy and Geodynamics，2008，28(2):92－94)

6 谷川，秦世伟.圆形隧道断面检测数据拟合新方法［J］.大地测量与地球动力学，2010(5):97－101.(A new method for fitting detection data of circular tunnel section［J］.Journal of Geodesy and Geodynamics，2010(5):97 －101)

7 王解先，季凯敏.工业测量拟合［M］.北京:测绘出版社，2008.(Wang Jiexian，Ji Kaimin.Industrial surveying fitting［M］.Beijing:Surveying and Mapping Press，2008)

A METHOD FOR TESTING 3D-CIRCLE BASED ON VECTOR

Zhao Pengfei
(Shanghai Surveying and Mapping Institute，Shanghai200063)

A new method for 3D-circle testing was presented.In the method，all observed points are fitted to a plane，and the sphere can be fitted by mid vertical planes，which are composed of the space vector，the 3D-circle center locates in the fitted plane.The coordinates of the center and the radius can be calculated by the method directly.The gross error will be eliminated during the fitting process.Compared with other methods，the method is very easy to realize，and reliability and fitting precision are higher.

testing of 3D-circle;plane fitting;mid vertical planes;sphere fitting;elimination of gross error

P258

A

1671-5942(2014)03-0072-03

2013-09-13

赵鹏飞，男，1985年生，工程师，硕士，主要从事精密工程测量和测量数据处理。E－mail:zpf_paper@163.com。