二乙基次膦酸铝的热分解动力学研究
2014-09-19邵先钊
邵先钊
(陕西理工学院化学与环境科学学院,陕西汉中 723000)
二乙基次膦酸铝的热分解动力学研究
邵先钊
(陕西理工学院化学与环境科学学院,陕西汉中 723000)
以TG-DTG为手段,研究二乙基次膦酸铝阻燃剂在氮气气氛中的热分解动力学;利用Kissinger-Akahira-Sunose(KAS)法、Flynn-Wall-Ozawa(FWO)法对其进行热分解动力学研究,计算出该阻燃剂的平均热分解表观活化能分别为260.2和259.4 kJ/mol;利用Šatava-Šesták法研究该阻燃剂的热分解机理属于相边界反应,得到其热分解动力学方程为g(α)=1 -(1 - α)1/3。
阻燃剂; 二乙基次膦酸铝; 热分解动力学; 机理
0引言
近年来,烷基次膦酸盐阻燃剂作为绿色环保阻燃剂的研究已成为磷系阻燃剂行业发展研究的热点之一[1-3]。将其添加到聚酰胺或尼龙等工程塑料中,可以达到UL94-V0的阻燃级别,并获得非常优越的机械加工性能、电性能,非常适合作为小型、薄壁、透明的电子电器原件材料。其中以德国克莱恩公司研发的二乙基次膦酸铝[(C2H5C2H5P(O)O)3Al]最具代表性[4-5]。关于烷基次膦酸盐的热分解与热稳定性的研究一直是研究人员非常关注的问题之一。国内外许多学者对于二乙基次膦酸盐与高分子复合阻燃材料的热稳定性和热分解机理进行了广泛而深入的研究[6-8],但都为定性研究,而在实际应用当中,人们更关心热分解与热稳定性方面的定量数据,以期能够对其研制和使用有所帮助。本论文运用热重法(TG)系统地研究了二乙基次膦酸铝(DEPA)的热分解动力学,采用Kissinger-Akahira-Sunose(KAS)、Flynn-Wall-Ozawa(FWO)、Kissinger和Šatava-Šesták法对其热分解的非等温动力学数据进行分析,求出其热分解表观活化能及指前因子,并推测可能的热分解机理和动力学方程。讨论了DEPA的结构对其热分解行为的影响,为其使用提供了必要的理论依据。
1 实验部分
1.1 试剂与仪器
阻燃剂二乙基次膦酸铝购于克莱恩公司。
TG-DTG分析在美国TA公司的SDT Q600上进行。实验条件:升温速率分别为10,20,30和40℃/min,氮气氛,气体流速为100 mL/min,升温范围室温至600℃,样品重量3~5 mg。
1.2 热分解动力学方法
基于非等温动力学理论并结合Arrhenius公式,热分解动力学方程通常可以表示为[9]:

式中:α为物质的转化百分率;β为升温速率(K/min);E为反应活化能(J/mol);R为气体常数,R=8.314 J·mol-1·K-1;T为绝对温度(K);A为表观指前因子(s-1)。
1.2.1 Kissinger-Akahira-Sunose(KAS 法)
KAS法[10-11]是一种常用的等转化率线性积分方法:

在不同的升温速率β下,选择相同的转化率α,则g(α)是一个定值,因此ln与之间呈线性关系,从其斜率即可求出活化能E值。该方法同其他积分法相比,在求解热分解动力学参数时,既不需要了解热分解机理,也不需要引入热失重微分数据,避免了因反应机理函数的假设不同可能带来的误差。
1.2.2 Flynn-Wall-Ozawa(FWO)等转化率法
FWO等转化率法[12-13]是另一种常用的积分方法,其最突出的优点在于不需要预先知道反应机理,避免了假设不同反应机理带来的误差,因此常被用来检验有假设的反应机理函数求出的活化能值。FWO等转化率法的公式如下:

对于同一反应体系,不同升温速率下选择相同的α,lg β与1/T呈线性关系,根据其斜率即可求得分解表观活化能Eα。
1.2.3 Kissinger法
Kissinger法[14]是研究热分解行为的微分方法,由多条DTG曲线的峰值温度Tp和升温速率β的关系来求解热分解表观活化能E。Kissinger法的表达式如下:

pE和指前因子A。

式中g(α)取自文献[16]中的30种机理函数形式。
计算中使用的实验数据与原始数据相同,对于固定的升温速率β,对应的Tj和αj的数值代入方程(5)中就得到包含k个的方程组
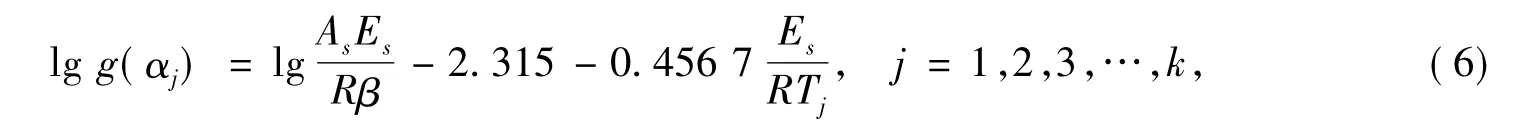
由于β固定,lg(AsEs/(Rβ))就是一个常数,所以方程组式(6)是一个线性方程组,从而可利用线性最小二乘法求解。
对于每个固定的β(10,20,30和40 K/min)和机理函数g(α),利用上述方法都可以计算出对应的Es和As值。通常,要求保留条件满足0<Es<400 kJ/mol的Es及其相应的lg As;分别用这些Es与FWO法计算出的Eo相比较,找出满足条件|(Eo-Es)/Eo|≤0.1的Es,分别用lg As与Kissinger法求得的lg Ak相比较,找出满足|(lg As-lg Ak)/lg Ak|≤0.2的lg As。对于上述符合要求的g(α),计算出相关系数和剩余方差值。
2 结果与讨论
2.1 DEPA的热分解过程
图1给出了DEPA在不同升温速率下的TG和DTG曲线,从图中可以看出随着升温速率的增加,DEPA的初始分解温度和DTG的峰值也同样升高,所有TG曲线的形状基本相同,可以说明DEPA的质量损失与加热速率无关,DEPA在400~550℃温度范围内分解,这对于聚合物的燃烧过程非常重要。即DEPA在添加到聚合物的加工过程中既不会提前分解,也不会在聚合物燃烧后分解,可以充分发挥阻燃的作用。

图1 DEPA在不同升温速率下的曲线
2.2 DEPA的热分解动力学
2.2.1 热分解表观活化能的计算
根据KAS法和FWO等转化率法、式(2)和式(3)可知,在相同的百分转化率时,热分解活化能可由曲线斜率求得。本文选用0.10~0.65的转化百分率,由实验数据拟合,得到一系列的曲线。图2给出了不同转化百分率时的拟合直线,各拟合直线近似平行,表明KAS法和FWO法均适用于所研究体系,图中各拟合直线的相关系数的平方在0.90以上。

图2 DEPA在不同转化率下的拟合曲线
如表1所示,由拟合直线的斜率计算得到活化能及相对误差R的平方。根据不同转化百分率所对应活化能的平均值,得出DEPA的平均活化能分别为260.2 kJ/mol(KAS法)和259.4 kJ/mol(FWO法)。在转化百分率在0.10~0.65范围内,活化能先增大,在α为0.40时,达到最大,然后活化能减少,直至DEPA分解结束。从键的离解能来看[17],CH—H(452 kJ/mol)、CH2—H(473 kJ/mol)、Al—O(512 kJ/mol)、P—C(513 kJ/mol)、P—O(597 kJ/mol)、C—C(607 kJ/mol),在高温下CH—H和CH2—H可能会同时断裂,接下来是Al—O和P—C键,最后是P—O和C—C键断裂。
2.2.2 热分解动力学模型的推测
表2是根据30种热分解机理函数g(α)在不同升温速率下的数据处理后得到对应的Es值和lg As值;分别用这些Es值与FWO法计算出的Eo值比较,找出满足条件|(Eo-Es)/Eo|≤0.1的E值,再分别用lg As与Kissinger法求得的lg Ak相比较,找出满足|(lg As-lg Ak)/lg Ak|≤0.2的lg A,计算发现文献[16]中的函数21最符合上述条件,取不同升温速率下所满足条件的平均值为 |(Eo- Es)/Eo|= 0.01,|(lg As-lg Ak)/lg Ak|=0.195,相关系数的平方为0.992,说明21号函数具有良好的线性关系,由此可得DEPA的热分解动力学方程为21号函数g(α)=1-(1-α)1/3。
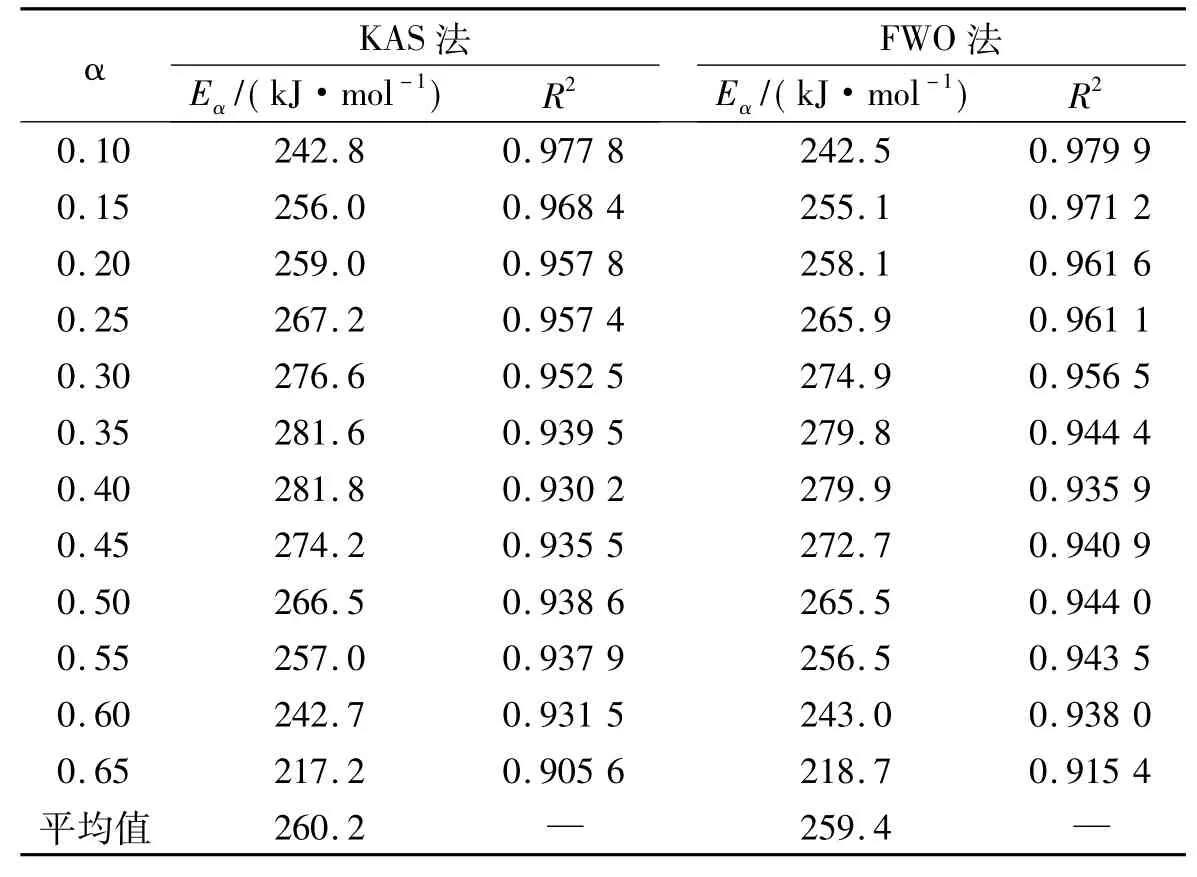
表1 不同转化百分率拟合曲线的活化能E和相关系数R的平方
表2 由atava-esták法计算30种机理函数的活化能和指前因子

表2 由atava-esták法计算30种机理函数的活化能和指前因子
指标 β/(K·min-1)12345678 Es/(kJ·mol-1) 10 448.5 478.2 489.4 511.8 127.9 123.8 413.6 380.8 ln As 10 30.80 32.74 32.93 34.61 8.15 7.94 27.21 24.72 R2 10 0.978 6 0.992 7 0.991 4 0.988 6 0.988 6 0.990 7 0.997 4 0.998 5 Es/(kJ·mol-1) 20 468.8 500.7 512.7 536.8 134.2 129.7 431.8 397.0 ln As 20 32.22 34.29 34.52 36.31 8.78 8.55 28.49 25.89 R2 20 0.995 5 0.996 0 0.996 0 0.995 7 0.995 7 0.996 0 0.994 5 0.992 8 Es/(kJ·mol-1) 30 474.8 507.0 519.1 543.5 135.9 131.4 437.3 402.1 ln As 30 32.45 34.52 34.76 36.55 8.97 8.74 28.73 26.12 R2 30 0.995 4 0.996 1 0.996 0 0.995 5 0.995 5 0.995 9 0.994 9 0.993 4 Es/(kJ·mol-1) 40 438.4 469.1 480.6 503.7 125.9 121.7 403.3 370.3 ln As 40 29.66 31.59 31.78 33.46 8.32 8.11 26.13 23.71 R2 40 0.995 7 0.982 9 0.984 3 0.986 6 0.986 6 0.985 0 0.974 8 0.970 2指标 β/(K·min-1) 9 10 11 12 13 14 15 16 Es/(kJ·mol-1) 10 273.2 182.1 136.6 91.07 1 093 68.30 546.4 819.6 ln As 10 18.64 12.20 9.02 5.89 77.54 4.36 38.17 57.83 R2 10 0.983 7 0.983 7 0.983 7 0.983 7 0.983 7 0.983 7 0.983 7 0.983 7 Es/(kJ·mol-1) 20 287.0 191.3 143.5 95.67 1 148 71.75 574.0 861.0 ln As 20 19.71 13.01 9.69 6.43 81.00 4.84 40.04 60.49 R2 20 0.994 3 0.994 3 0.994 3 0.994 3 0.994 3 0.994 3 0.994 3 0.994 3 Es/(kJ·mol-1) 30 290.6 193.7 145.3 96.86 1 162 72.64 581.1 871.7 ln As 30 19.91 13.20 9.88 6.61 81.30 5.02 40.28 60.76 R2 30 0.993 9 0.993 9 0.993 9 0.993 9 0.993 9 0.993 9 0.993 9 0.993 9 Es/(kJ·mol-1) 40 269.8 179.9 134.9 89.94 1 079 67.46 539.7 809.5 ln As 40 18.37 12.23 9.19 6.20 74.67 4.75 37.04 55.83 R2 40 0.989 0 0.989 0 0.989 0 0.989 0 0.989 0 0.989 0 0.989 0 0.989 0
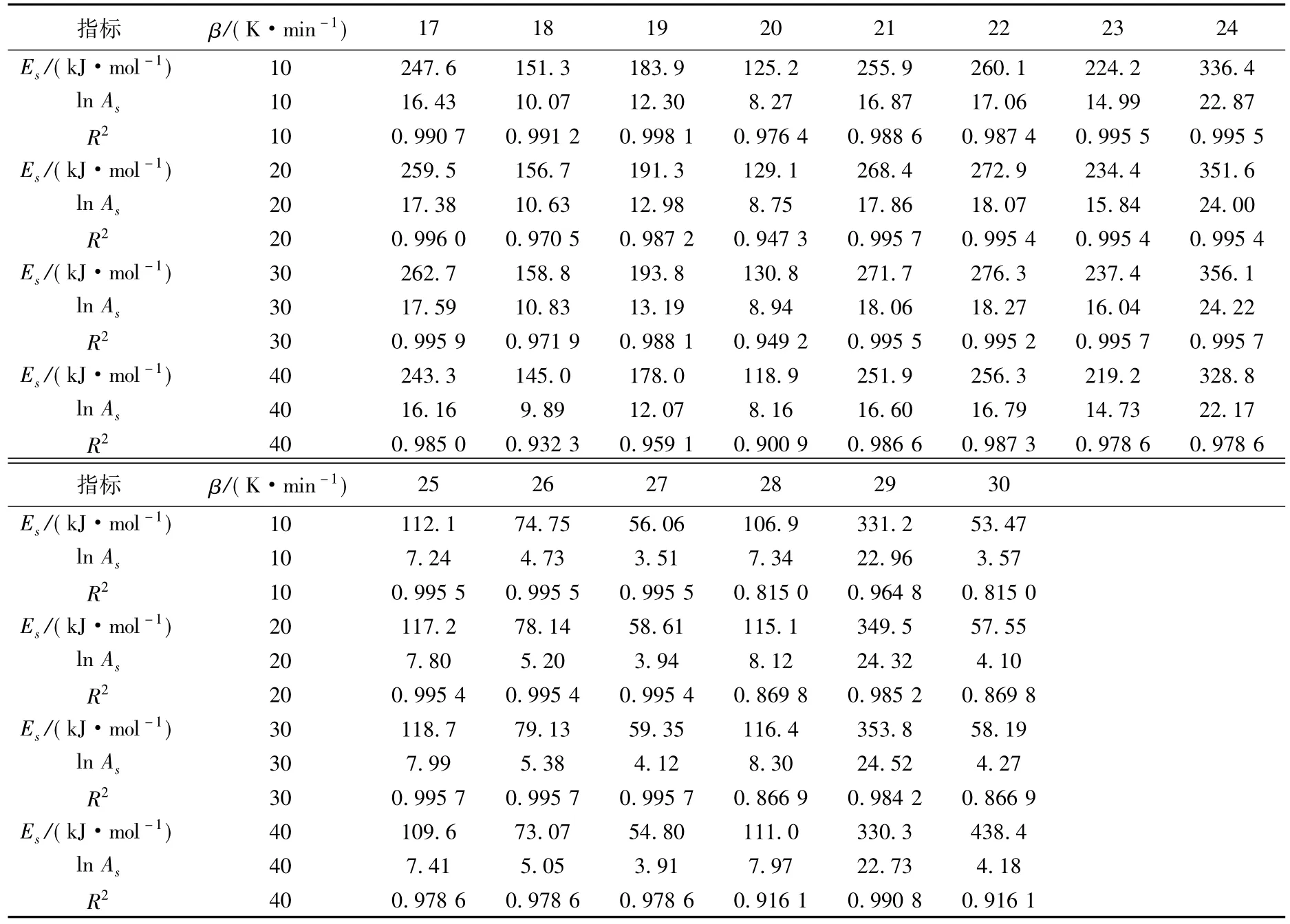
续表
3 结论
通过TG-DTG方法对阻燃剂二乙基次膦酸铝的热分解动力学进行了研究,利用KAS法、FWO法求出的表观活化能为260.2 kJ/mol和259.4 kJ/mol,两种不同方法获得的平均活化能较接近。转化百分率在0.10~0.40范围内时,表观活化能逐渐增加,而大于0.40时表观活化能呈现下降趋势,直至DEPA分解结束。通过Šatava-Šesták法得到其热分解动力学方程为g(α)=1-(1-α)1/3,是相边界反应。
[1]许冬梅,欧育湘.新一代阻燃剂次膦酸盐阻燃的玻纤增强尼龙66[J].塑料,2005,34(2):70-73.
[2]刘鹏,王忠卫,刘波,等.一种新型次膦酸盐阻燃PA6的制备及其阻燃性能[J].塑料,2010,39(2):111-113.
[3]ELMAR S.Phosphorus-based flame retardants for thermoplastics[J].Plastics,Additives and Compounding,2007,9(3):26-30.
[4]鲍尔 H,克劳斯 W,西肯 M,等.二烷基次膦酸盐:中国,1660857[P].2005-08-31.
[5]威夫林 N,施米茨 H P,科尔布 G.制备二烷基次膦酸的方法:中国:1280584A[P].2001-01-17.
[6]BRAUN U,SCHARTEL B,FICHERA M A.Flame retardancy mechanisms of aluminium phosphinate in combination with melamine polyphosphate and zinc borate in glass-fibre reinforced polyamide 6,6[J].Polymer Degradation and Stability,2007,92(8):1528-1545.
[7]DUQUESNE S,FONTAINE G,Cérin-Delaval O,et al.Study of the thermal degradation of an aluminium-phosphinate aluminium trihydrate combination[J].Thermochimica Acta,2013(551):175-183.
[8]SEEFELDT H,DUEMICHEN E,BRAUN U.Flame retardancy of glass fiber reinforced high temperature polyamide by use of aluminum diethylphosphinate:thermal and thermo-oxidative effects[J].Polymer International,2013,62(11):1608-1616.
[9]VYAZOVKIN S,BURNHAM A K,CRIADO J M,et al.ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data[J].Thermochimica Acta,2011(520):1-19.
[10]KISSINGER H E.Reaction Kinetics in differential thermal analysis[J].Analytical Chemistry,1957,29(11):1702-1706.
[11]AKAHIRA T,SUNOSE T.Method of determining activation deterioration constant of electrical insulating materials[J].Chiba Institute of Technology:Sci.Technol,1971(16):22-31.
[12]FLYNN J H,WALL L A J.A quick,direct method for the determination of activation energy from thermogravimetric data[J].Polymer Science Part B:Polymer Letter,1966(4):323-328.
[13]OZAWA T B.A new method of analyzing thermogravimetric data[J].Chemical Society of Japan,1965(38):1881-1816.
[14]KISSINGER H E.Variation of Peak temperature with heating rate in different rate in differential thermal analysis[J].Journal of research of the National Bureau of Standards,1956(57):217-221.
[15]Škvára F,Šesták J.Computer calculation of the mechanism and associated kinetic data using a non-isothermal integral method[J].Journal of Thermal Analysis and Calorimetry,1975(8):477-489.
[16]胡荣祖,高胜利,赵凤起,等.热分析动力学[M].北京:科学出版社,2008:63-64.
[17]WYOMING L.Lange’s Handbook of Chemistry[M].16th ed.New York:McGraw-Hill,2005.
[责任编辑:谢 平]
Thermal decomposition kinetics of aluminum diethylphosphinate
SHAO Xian-zhao
(School of Chemistry and Environment Science,Shaanxi University of Technology,Hanzhong 723000,China)
The thermal decomposition kinetics of the aluminum diethylphosphinate(DEPA)flame retardant was studied by TG-DTG techniques.The kinetic parameters,including the activation energy and frequency factor of the decomposition process for the compound were calculated through the Kissinger-Akahira-Sunose(KAS)and Flynn-Wall-Ozawa(FWO)method and the thermal decomposition mechanism was also studied with the Šatava-Šesták method.The results show that the activation energy was 260.2 kJ/mol and with the KAS method and 259.4 kJ/molwith the FWO method respectively.The thermal decomposition mechanism belongs to phase boundary reaction and the kinetic equation of the novel flame retardant can be expressed as g(α)=1 -(1 -α)1/3.
organphosphorus flame retardant; aluminum diethylphosphinate; thermal decomposition kinetics; mechanism
O642.3
A
1673-2944(2014)05-0034-06
2014-03-25
陕西理工学院博士人才引进启动经费项目资助(SLGQD13(2)-2)
邵先钊(1983—),男,山东省单县人,陕西理工学院讲师,博士,主要研究方向为环保型阻燃剂的开发。
