石墨烯的晶格振动与导热机理的研究
2014-09-19任亚杰黄文登
任亚杰, 黄文登
(陕西理工学院物理与电信工程学院,陕西汉中 723000)
石墨烯的晶格振动与导热机理的研究
任亚杰, 黄文登
(陕西理工学院物理与电信工程学院,陕西汉中 723000)
石墨烯具有独特的结构和导热性质,在微电子领域也具有巨大的应用潜力。采用价力场方法研究石墨烯中的晶格振动,得出了石墨烯晶格振动的频率方程,计算出了石墨烯内光学声子与声学声子的色散曲线。探讨了石墨烯的导热机理,得出晶格振动的剧烈程度、石墨烯的尺寸、温度和基底等是影响石墨烯导热性能的主要因素。
石墨烯; 晶格振动; 导热性能
0引言
石墨烯(Graphene)又叫单层石墨,是构造其他石墨材料的最基本的材料单元。因为具有非同寻常的导电和导热性能,使石墨烯在微电子领域也具有巨大的应用潜力,有可能会成为硅的替代品,制造超微型晶体管,有望在高性能的光电子器件、集成电路和气体传感器等领域获得广泛应用。石墨烯已经成为研究的热点,人们已经采用机械剥离、电弧和化学气相沉积等方法制备出了各种尺寸的石墨烯材料[1-3]。
石墨烯是一种典型的二维平面材料,其理想晶体结构如图1所示,最近邻有3个原子,是平面六边形点阵,可以看作是一层被剥离的石墨分子,每个碳原子均为sp2杂化,并贡献剩余一个p轨道上的电子形成大π键,π电子可以自由移动,赋予石墨烯良好的导电性。二维石墨烯结构可以看是形成所有sp2杂化碳质材料的基本组成单元[4-6]。在石墨烯中,碳原子在不停的振动,振动的幅度有可能超过其厚度。石墨烯的晶格振动影响石墨烯的形貌特征,已有的研究[7-9]表明,石墨烯在垂直于原子平面方向上经波动后,结构变得更加稳固,尤其是单层石墨烯因为降低了其表面能,形态结构由二维向三维形貌转换,产生褶皱,褶皱是二维石墨烯存在的必要条件。石墨烯的晶格振动不仅仅影响石墨烯的形貌特征,还影响的石墨烯的力学性质、输运特性、热学性质和光电性质[10-11]。因此,有必要对石墨烯的晶格振动及其相关性质进行研究。本文采用价力场方法研究石墨烯中的晶格振动,计算了石墨烯内光学声子与声学声子的色散曲线,探讨了石墨烯的导热机理以及影响石墨烯导热性能的主要因素。
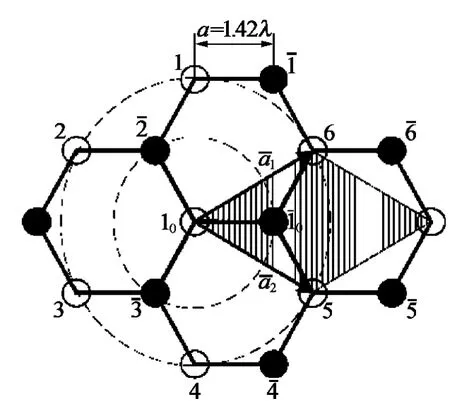
图1 石墨烯的晶体结构图
1 石墨烯的晶格振动

考虑标号为 10的原子,它的最近邻原子有 3 个(标号为),第二近邻原子有 6 个(标号为 1,2,3,4,5,6)。第一近邻原子的坐标分别为

根据经典的量子理论,固体的热容量主要是由晶格振动能引起的(主要是声学声子的贡献),在高温的情况下,需考虑光学声子的贡献,在极低温度的情况下,需考虑电子运动对热容量的贡献。石墨烯是一种层状结构材料,其晶格和原胞如图1所示,原胞基矢为
第二近邻原子的坐标分别为

对石墨烯的热学性质的影响主要是石墨烯晶格振动。
下面运用价力场方法[8](valence force field method)来探讨石墨烯的晶格振动。
在价力场方法中,石墨烯内所有原子间的相互作用力可以分为键的伸缩力和键的弯曲力。相互作用势能可以写为
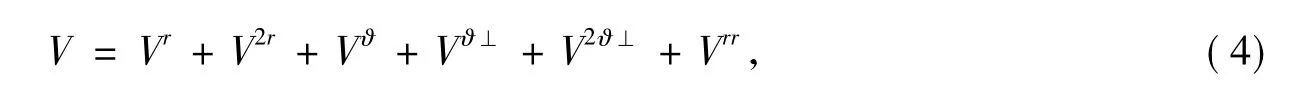
式中Vr表示第一近邻原子间(N-type)的伸缩势能,定义为

δrij是最近邻两个原子(j)的键的伸长。第二近邻原子间(F-type)的伸缩势能为
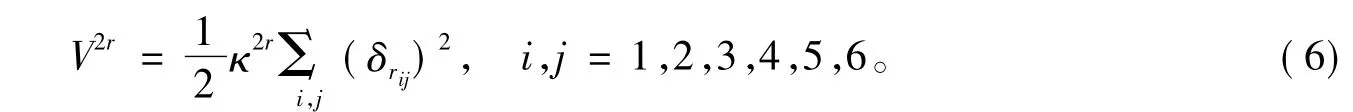
最近邻原子的平面内键弯曲势能为

δϑijk是成键原子(j-,j-)的键角的微小变化。最近邻原子(N-type)在平面外的键弯曲势能为

式中ua(i)和ub()分别为处在(i)位置处的原子位移矢量。第二近邻原子的平面外的键弯曲势能为

高价的伸缩相互作用势能可以用下式进行描述:

用力常数的定义

可以得到下面的动力学矩阵:


其中uα(10)、uα()为第一个和第二布拉菲格子原子的振幅。引入一种新变量

将式(13)和(14)代入动力学矩阵(12),可以得到石墨烯的声子的6个振动频率方程

考虑到石墨烯有两个布拉菲格子,可以定义原子的偏离平衡位置的位移为
在上面的方程中,在长波极限下(小波矢q)的情况下,w表示的是声学声子,描述的是原子(10,)的同相运动,v表示的是光学声子,描述的是原子(10)的反相运动。对于较大的波矢,声学声子和光学声子的行为变得很类似。根据克莱姆法则,可从上面6个方程的系数行列式等于0得到声子的本征频率 ws(q)。式中决定相互作用势能的参数 κr、κ2r、κϑ与 κϑ⊥、κ2ϑ⊥、κrr可以从色散曲线与试验数据的对比得到,石墨烯平面内的力常数假定相同,波矢q限制在第一布里渊区,其倒格子基矢量为

这两个基矢量与它们的和

在图1 中可以看出,其中 bi= ΓΓi,i=1,2,…,6。布里渊区高对称点Γ到石墨烯晶胞的任一边的中点的长度为

通过求解方程(15),我们可以得到6支极性声子(见图2)。这些声子主要有:平面外(垂直于石墨烯单原子层平面)的声学声子(ZA)和光学声子(ZO),它们的位移矢量沿着z轴方向;石墨烯平面内的横向声学声子(TA)和横向光学声子(TO);石墨烯平面内的纵向声学声子(LA)和纵向光学声子(LO)。石墨烯的声子特性与金属、半导体中的声子特性[12-13]不一样,表现出独特的特性,这主要由石墨烯的二维复式晶体结构决定。有价力场方法的声子曲线与第一原理计算结果和试验结果符合得很好[14-15]。

图2 石墨烯内光学声子(LO、TO和ZO)与声学声子(LA、TA和ZA)的色散曲线
2 石墨烯的热学性质
导热系数是描述热学性质的一个重要物理量,下面从经典的热学理论出发,对石墨烯的导热系数进行研究。石墨烯薄片的热通量表达式为[9]

式中vħω为一个声子所带的能量,N(q,ω)为热流中的声子数目,可由玻尔兹曼方程得出。根据热导的宏观定义

其导热系数是一个张量,为

式中dx和dy为样品的宽度和长度。可以写出导热系数的对角张量为

考虑二维声子态密度,我们得到标量导热系数

上面理论计算的导热系数主要由石墨烯的声子频率、声子的支数和声子的作用过程等决定。结合前面价力场方法得出的声子频率的结果,通过公式(21)可以计算出导热系数(如图3)。图3给出了不同宽度的石墨烯薄片的导热系数与温度的关系。可以从图中看出来石墨烯的导热系数随温度的增加而减小。在同一温度下,导热系数随石墨烯的宽度的增加而增加。由经典的热传导理论可知,随着温度的升高,晶格振动加强,声子运动剧烈,热流中的声子数目也增加。声子间的相互作用或碰撞更加频繁,原子偏离对平衡位置的振幅增大,引起的声子散射加剧,使导热载体(声子)的平均自由程减小。这是石墨烯的导热系数随温度升高而降低的主要原因。对于石墨烯,电子的运动对导热也有一定的贡献,但在高温情况下,晶格振动对石墨烯的导热贡献是主要的,起主导作用。
一些试验研究[4,11]给出的石墨烯的导热系数经验公式为

式中Xg是温度系数,L是单层石墨烯的中间部分与散热片之间的距离,h是单层石墨烯的厚度,d为单层石墨烯的宽度,δf是G峰位移,δP是样品的热功率的变化。从经验公式可以看出,石墨烯的导热系数(导热性能)主要受3个因数的影响:单层石墨烯的尺寸效应,温度,石墨烯生长的基底材料。一些实验[4,7]也证实了石墨烯的导热系数随石墨烯的尺寸增加而增加,随温度的升高而减小,基底材料不同,其导热系数也不同。
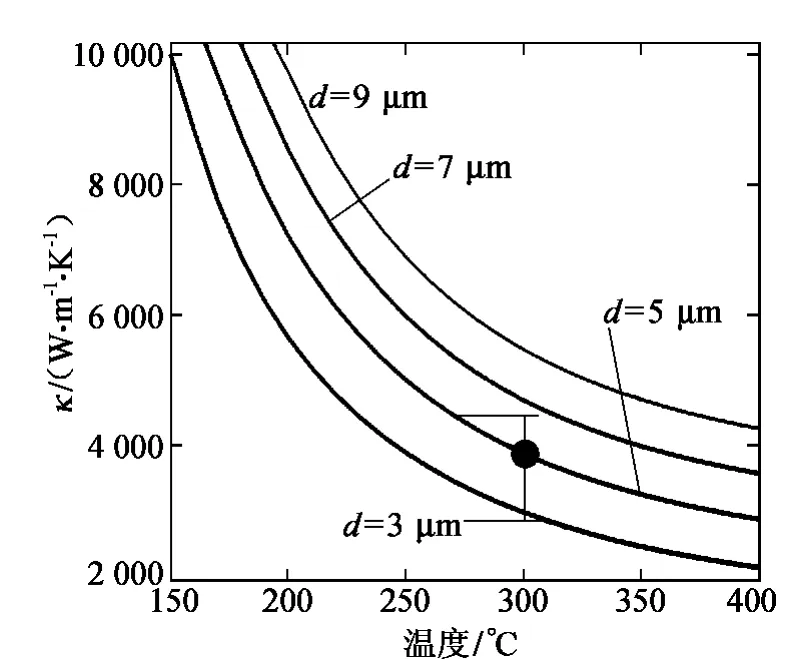
图3 不同宽度的石墨烯薄片的导热系数与温度的关系
3 结论
石墨烯具有很好的导热性能,在导热的过程中,晶格振动起主要作用。其导热系数是温度、尺寸的函数。石墨烯由于具其优良的导热性能,具有广泛的应用前景。其导热性能主要受石墨烯的尺寸、温度、基底的影响。但由于石墨烯种类的繁多和性能的可调控性,深入研究石墨烯结构变化和各种性能是一项长期的工作。石墨烯制备不同的方法、纯度、分散状态、规格尺寸(纵横比)等可能导致同一测试模型得到不同的测试结果,因此深入研究石墨烯具有较为重要的意义,特别是研究石墨烯的热物性是超高温热防护材料设计中不可缺少的数据。
[1]WANG Zhi-yong,LI Nan,SHI Zu-jin,et al.Low cost and large scale synthesis of graphene nanosheets by arc discharge in air[J].Nanotechnology,2010,21(17):2-6.
[2]LI X S,MAGNUSON C W,VENUGOPAI A,et al.Large area graphene single crystals grown by low pressure chemical vapor deposition of methane on copper[J].J.Am.Chem.Soc.,2011,133(9):16-19.
[3]JUANG Zhen-yu,WU Chih-yu,LU Ang-yu,et al.Graphene synthesis by chemical vapor deposition and transfer by roll to roll process[J].Carbon,2010,48(11):69-72.
[4]BERGER C.Electronic confinement and coherence in patterned epitaxial graphene[J].Science,2006,312(5777):91-96.
[5]GEIM A K,GRIGORIEVA I V.Vander Waals heterostructures[J].Nature,2013,499(7459):19-25.
[6]MEYER J C.The structure of suspended grapheme sheets[J].Nature,2007,446(7131):60-63.
[7]周春玉,曾亮,吉莉,等.石墨烯及其复合材料导热性能的研究现状[J].材料开发与应用,2010,25(6):94-100.
[8]NIKA D L,POKATILOV E P,ASKEROV A S,et a1.Phonon thermal conduction in graphene:Role of Umklapp and edge roughness scattering[J].Physical Review B,2009,79(155413):1-12.
[9]Bhandari C M,Rowe D M.Thermal Conduction in Semiconductors[M].New York:Wiley,1988:20-22.
[10]NIKA D L,GHOSH S,POKATILOV E P,et al.Lattice thermal conductivity of graphene flakes:comparison with bulk graphite[J].Applied Physics Letters,2009,94(20):103-106.
[11]GUO Zhi-xin,ZHANG Dier,GONG Xin-gao.Thermal conductivity of graphene nanoribbons[J].Applied Physics Letters,2009,95(16):163103.
[12]HUANG Wen-deng,CHEN Guang-de,YE Hong-gang,et al.Effect of ternary mixed crystals on interface optical phonons in wurtizte InxGa1-xN/GaN quantum wells[J].J.Appl.Phys.,2012,112(5):053704
[13]HUANG Wen-deng,CHEN Guang-de,YE Hong-gang,et al.Ternary mixed crystal effects on interface optical phonon and electron-interface optical phonon coupling in wurtzite GaN/AlxGa1-xN quantum wells[J].Optical Material,2013,35(8):71-76.
[14]SEOL J H,JO I,MOORE A L,et al.Two-dimensional phonon transport in supported graphene[J].Science,2010,328(5975):13-16.
[15]BORYSENKO K M,MULLEN J T,BARRY E A,et al.First-principles analysis of electron-phonon interactions in graphene[J].Physical Review B,2010,81(12):12-16.
[责任编辑:魏 强]
The lattice vibration and thermal properties of graphene
REN Ya-jie,HUANG Wen-deng
(School of Physics and Telecommunication Engineering,Shaanxi University of Technology,Hanzhong 723000,China)
Graphene has a unique structure and thermal-conductive properties.The lattice vibrations of graphene are investigated by the valence force field method.The dispersion curves of optical phonon and acoustic phonon in graphene are calculated.The thermal conductivity of graphene is also discussed.The lattice vibration of graphene is a major cause in affecting the thermal conductivity of graphene.
graphene; lattice vibrations; thermal conductivity
O471.4;O471.3
A
1673-2944(2014)05-0068-05
2014-05-28
国家自然科学基金资助项目(51106093);陕西省教育厅科学研究计划项目(12JK0972)
任亚杰(1964—),男,陕西省洋县人,陕西理工学院教授,硕士,主要研究方向为凝聚态理论;黄文登(1978—),男,陕西省镇巴县人,陕西理工学院副教授,硕士,硕士研究生导师,主要研究方向为半导体物理学。
