微波布拉格衍射中立方晶体晶面衍射测量与模型选取讨论
2014-09-19徐春阳陈文婷王晓栋张志华
徐春阳,陈文婷,王晓栋,张志华,方 恺,赫 丽
(同济大学物理科学与工程学院,上海 200092)
微波布拉格衍射中立方晶体晶面衍射测量与模型选取讨论
徐春阳,陈文婷,王晓栋,张志华,方 恺,赫 丽
(同济大学物理科学与工程学院,上海 200092)
在微波布拉格衍射实验中,通过对立方晶体模型晶格常数参量选取,测定(110)面入射角与衍射强度变化关系,来验证衍射极大值在随入射角变化而变化的过程是否满足布拉格定律.同时可在一定入射角变化范围内,限定衍射级数的大小,讨论只改变接收端角度时,(100)面与(110)面衍射极大值时晶格常数所在范围,并从理论上给出同时测定两晶面可限定的衍射级数与晶格常量的范围.
微波;布拉格衍射;立方晶体;晶面
1 引 言
布拉格衍射,又称X射线衍射的布拉格形式,最早由威廉·劳伦斯·布拉格及威廉·亨利·布拉格于1913年提出,他们早前发现了固体在反射X射线后产生的晶体线,而这项定律正好解释了这样一种效应.他们发现,这些晶体在特定的波长及入射角时,反射的辐射会形成集中的波峰,称布拉格尖峰.布拉格衍射也适用于中子衍射及电子衍射[1].用微波模拟X射线,入射到晶体模型时衍射的现象,同X射线对晶体的布拉格衍射现象相似.微波模拟布拉格衍射实验中,通过入射一定频率的微波,投射到相应点阵组成的晶面上,发生布拉格衍射,接收测定相应衍射波强度来反应衍射强度[2-3].
本文以晶格常量变化验证立方晶体中(110)晶面衍射极大值对应入射角由布拉格公式得到微波波长,与讨论探究接收端同时测定(100)面与(110)面衍射波晶格常量范围为两主要目的,对微波布拉格衍射实验进行一定程度的拓展与补充.
2 仪器与原理概述
2.1 实验仪器
实验采用微波分光计装置进行实验,按图1组装仪器.
微波信号源选用等幅工作状态,提供单一波长微波,λ=32.02 mm.
衰减器改变发射微波幅度,刻度盘指数越大,对微波衰减越大,输出信号越小.
振荡器波导口输出微波信号由发射喇叭发射,发射喇叭发射信号的电矢量偏振方向与发射喇叭窄边平行,安装在固定臂上.
经过晶面衍射,调整活动臂角度接收喇叭可接收到相应微波信号,由二极管整流后输出直流信号,微安表可显示经整流输出的直流电信号[4].

图1 微波布拉格实验装置示意图
2.2 实验原理
当电磁辐射或亚原子粒子波的波长,与进入的晶体样本的原子间距长度相若时,就会产生布拉格衍射,入射物会被系统中的原子以镜面形式散射出去,并会按照布拉格定律进行相长干涉.对于晶质固体,波被晶格平面所散射,各相邻平面间的距离为d.当被各平面散射的波进行相长干涉时,它们的相位依然相同,因此每一波的路径长度皆为波长的整数倍.进行相长干涉两波的路径差为2d sinθ,其中θ为散射角.由此可得布拉格定律产生相长干涉的条件[5]:

整数时,才是极大干涉.式(1)称为晶体衍射的布拉格公式.
实验中选取最简单晶体结构(如图2所示),2种易于进行测量的晶面,(100)面和(110)面.一般而言,晶面指数为(n1n2n3),其相邻的2个晶面间距为,a为晶格常量,即晶胞边长.实验中通过设置一定的参量a选取适合3 cm微波布拉格衍射的晶体模型.

图2 最简立方晶面示意图
3 参量讨论与实验探究
3.1 (100)面和(110)面测定异同
(100)面和(110)面在本实验中成45°角[7],当选取法线方向垂直于(110)时,各个晶面与法线方向角度关系如图3所示.

图3 (100)面和(110)面衍射时角度关系
当用入射角β代替散射角θ时,(1)式改写为
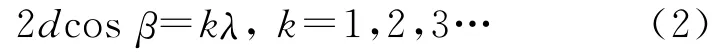
在测定(100)晶面衍射极大值时,晶面即平行于相应点阵组成的外表面,在选定一定范围内的入射角时,相应法线与反射角组成的平面与晶体模型(100)面点阵组成表面垂直,测定(100)面入射角β与衍射强度I关系时在20°~70°间可以得到1级衍射极大值与2级衍射极大值.对应k=1,2代入(2)式,得到衍射级数对应的入射角.以a=4.0 cm晶体模型为例计算(100)晶面1级衍射极大、2级衍射极大所对应的入射角β理论值为66.4°与36.8°.
在测定(110)晶面衍射极大值时,法线方向与测定(100)晶面时法线方向相差45°.由(2)式移项可得

即衍射级数与晶面间距需满足的条件.
现有a=3.4 cm与a=4.0 cm晶体模型,对应晶面间距d设为d1,d2,此时d=a/,d1=2.4 cm,d2=2.8 cm.λ=32.02 mm:当k=1时,λ/2d1<1与λ/2d2<1均满足(3)式条件;当k=2时,2λ/2d1>1与2λ/2d2>1,均不满足(3)式条件.由此可得当k=3,4,5…均不能满足(3)式条件,即所选取2个不同晶格常量的晶体模型,测定(110)面衍射极大值时,只有1级衍射极大.
3.2 不同晶格常量的(110)面衍射极大值测定
选取a=3.4 cm晶体模型,当法线方向垂直于晶体模型(110)面时,调整入射角,通过旋转活动臂使之与法线方向夹角与入射角相等,测定入射角与衍射波强度关系,得到表1.通过作图软件得到(110)面入射角β与衍射强度I关系曲线,如图4(a)所示.

表1 (110)面入射角β与衍射强度I变化关系

图4 (110)面入射角β与衍射强度I关系曲线
由(3)式通过入射角β与衍射强度I关系曲线可得1级衍射极大值对应入射角所求得的微波波长为

相对偏差为:
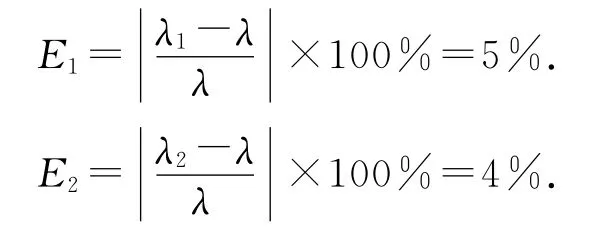
选取a=4.0 cm晶体模型,入射波经(110)晶面衍射后透过挡板到达接收喇叭,通过旋转活动臂使之与法线方向夹角与入射角相等,通过微安表读出示数,测定入射角与衍射波强度关系得到表1.通过作图软件得到(110)面入射角β与衍射强度I关系曲线,如图4(b)所示.
由(3)式通过入射角β与衍射强度I关系曲线可得1级衍射极大值对应入射角所求得的微波波长.
a=3.4 cm与a=4.0 cm两晶格常量不同的晶体模型在微波布拉格衍射中测定(110)面1级衍射极大值对应入射角计算所得的微波波长与理论波长吻合较好,在实验仪器与测量精度允许误差范围内,实验结果符合布拉格衍射定律.
3.3 接收端同时测定(100)面与(110)面衍射波参量讨论
3.3.1 角度限定与参量讨论
对于每一入射角β,当不改变晶体模型角度,只旋转接收喇叭,欲接收(100)面与(110)面衍射强度.由图3分析,当入射波为CO时,设OB为起始边,图示θ角度值在(0,45°)间.当测定(110)面时,θ取值范围在(0,90°)间,入射角β为90°-θ;当测定(100)面时,θ取值范围在(-45°,45°)间,入射角β为45°-θ.则θ取值范围限定在(0,45°)内,(100)面满足
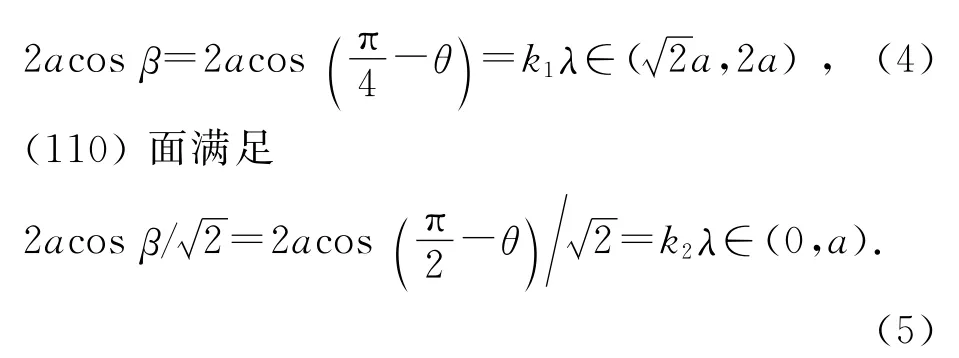
由(4)式(5)式限定关系,讨论k1和k2取值关系.
1)k1=k2=1测量情况讨论
当k1=k2=1时,(5)式极大值a小于(4)式极小值,不可能满足晶面角度不变,同时测量(100)面与(110)面1级衍射极大值.
2)k1=2,k2=1测量情况讨论
当k1=2,k2=1时,满足同时测量两晶面衍射极大值条件,即(4)式满足式满足λ∈(0,a),(100)面测定2级衍射极大值,(110)面测定1级衍射极大值时,晶格常量可满足范围为

可以同时测定(100)面2级衍射极大与(110)面一级衍射极大.
3.3.2 同时测定两晶面衍射波意义与局限性
对于每一入射角β,当采用不改变模型角度,只旋转接收喇叭,测定(100)面和(110)面衍射极大时,可以减少因模型角度转动造成的误差,在测定微波波长过程中,可以提高测量效率,为观测带来便利.同时,因模型转动角度有限,在观测微波布拉格衍射取较大范围散射角衍射强度变化情况时,并不适用.
4 结 论
通过对立方晶体中(110)面晶体模型尺寸参量选取,测定入射角与衍射强度变化关系,结果较好地满足了实验预期.不同晶格常量的改变符合布拉格定律反映的衍射级数与微波波长的关系.探究接收端同时测定(100)面与(110)面衍射波参量讨论也给出了相应衍射级数与晶格常量所取范围的关系,在微波布拉格散射实验中,为测定与探究(100)面与(110)面衍射极大值与测定微波波长提供新思路.
[1] Cowley J M.Diffraction physics[M].Amsterdam:North-Holland,1975:123-144.
[2] 余伟超,杜艾,张志华,等.窄缝条件下影响微波单缝衍射图样的主要因素[J].物理实验,2013,33(2):37-40.
[3] 吴俊,吴本科,谢莉莎,等.微波单缝衍射的实验研究及数值模拟[J].物理实验,2008,28(6):39-41.
[4] 同济大学物理实验中心.近代物理实验讲义[Z].上海:2014:35-40.
[5] Myers H P.Introductory solid state physics[M].London:Taylor&Francis,2009:52.
[6] 陆栋,蒋平,徐至中.固体物理学 [M].上海:上海科学技术出版社,2003:8-10.
[7] 何颖卓,香莲,李春芝.关于微波布拉格衍射实验中(110)晶面衍射极大值测量的探讨[J].长春理工大学学报(自然科学版),2013,36(1/2):62-65.
[责任编辑:郭 伟]
Measuring cubic crystal diffraction and choosing cubic model crystal in microwave Bragg diffraction
XU Chun-yang,CHEN Wen-ting,WANG Xiao-dong,ZHANG Zhi-hua,FANG Kai,HE Li
(School of Physics Science and Engineering,Tongji University,Shanghai 200092,China)
In microwave Bragg diffraction experiments,by changing the lattice constant of the cubic model crystal,measuring the relationship between the incident angle and the diffraction intensity of(110)plane,the Bragg law was verified.Meanwhile,for limited diffraction orders,the range of the lattice constants of(100)and(110)planes was discussed when only the receiver angle was changed,and the limitation on the range of the diffraction orders and lattice constants were also presented in detail.
microwave;Bragg diffraction;cubic crystal;crystal face
O436.1
A
1005-4642(2014)10-0045-04
“第8届全国高等学校物理实验教学研讨会”论文
2014-06-24;修改日期:2014-07-20
同济大学教学改革研究与建设项目;同济大学精品实验项目
徐春阳(1993-),男,北京人,同济大学物理科学与工程学院应用物理专业2011级本科生.
王晓栋(1984-),男,江苏江阴人,同济大学物理科学与工程学院助理教授,博士,主要从事材料物理方面研究和大学物理教学工作.
