不同形式齿廓偏差对直齿轮副振动的影响规律
2014-09-19常乐浩吴立言贺朝霞
常乐浩,刘 更,吴立言,贺朝霞
(1.西北工业大学 陕西省机电传动与控制工程实验室,西安 710072;2.长安大学 道路施工技术与装备教育部重点实验室,西安 710064)
齿轮制造误差是引起齿轮系统振动的重要激励形式之一,研究误差激励形成的机理和性质对准确预测齿轮系统振动和噪声具有重要意义。在齿轮系统动力学分析时,齿轮的短周期制造误差常以综合啮合误差表示。由于齿轮误差的随机性特点,以往文献常用简谐函数模拟综合误差函数[1-2]。然而,多数学者在误差幅值确定时都进行了回避,或直接采取假设的方式,缺少合理的理论依据。由于重合度和啮合轮齿间变形的相互影响,误差的实际作用量应该小于原始齿面误差幅值,直接利用精度等级确定的综合误差幅值显然过大。韩静波考虑重合度对齿廓偏差的影响,提出了齿廓偏差和基节偏差的合成方法,并应用于行星齿轮系统动力学分析中[3]。但这种方法未考虑不同载荷下轮齿变形的影响,而且无法分析当齿面具有不同误差分布形式时系统动态响应的差异。Matsumura等[4]在研究斜齿轮振动特性时,发现中凸齿廓的齿轮具有较小的振动。李凯岭等[5]研究了齿廓偏差对直齿轮副啮合噪声的影响规律,发现轮齿具有不同形式齿廓偏差时的噪声差别显著,但其研究基于试验测试结果,缺少合理的数学模型和理论分析。
本文基于齿轮承载接触分析模型,提出了齿轮综合啮合误差的确定方法。同时考虑啮合刚度激励、误差激励和啮入冲击激励,分析了具有不同形式齿廓偏差时直齿轮副的动态响应规律,为进一步提出齿廓偏差控制原则奠定了理论基础。
1 综合啮合误差的确定
齿轮副的啮合过程为两弹性体的动态接触过程,两弹性体的通用承载接触分析模型如图1所示。当实际齿廓与理想齿廓存在偏差时,可能接触点i需要满足变形协调条件[6]:

式中:ui为接触体上点i的总弹性变形,大小为ui1和ui2之和;εi为接触前点i的原始间隙,即原始齿面误差;δ为两接触体的刚体接近量,即静态传递误差;Yi为接触后点i的剩余间隙。

图1 两弹性体承载接触模型Fig.1 Loaded contact model of two elastic bodies
将所有接触点对均利用式(1),并写成矩阵形式为

式中:[λ]为弹性变形柔度矩阵;{F}为离散接触点载荷向量;{Y}为剩余间隙向量;{ε}为原始齿面误差向量;N为可能接触点总数。
齿轮在接触点的弹性变形实际上由宏观变形(主要为弯曲变形)和局部接触变形组成。假设弯曲变形随载荷呈线性变化,而接触变形随载荷呈非线性变化,则可将式(2)的变形协调条件写为:

式中:[λb]为弯曲变形柔度矩阵;{uc}为各接触点接触变形向量。
齿轮副在接触时还需要满足载荷平衡条件:

式中:I为各元素为1的行向量;P为啮合法向力。
各点载荷与剩余间隙之间满足以下接触条件:

各接触点的柔度系数可利用有限元法计算,并利用文献[7]的方法将弯曲变形分离出来。各离散点的接触变形用各点所在分段接触线的接触变形代替。有限长线接触弹性接触变形的解析计算公式[8]为

式中:li为分段接触线长度;E1和E2分别为两齿轮材料的弹性模量;ν1和ν2分别为两齿轮材料的泊松比;R1和R2分别为两齿轮接触点法向曲率半径。
式(3)~(4)组成的N+1阶非线性方程组含有{F},{Y}和 δ共2N+1个未知数,但由于接触条件(5)的存在,方程组有唯一解。因为后续计算中并不关注剩余间隙{Y}的大小,这样在求解过程中可不必求解{Y},从而减少了未知量的个数。本文采用迭代法求解{F}和δ,迭代流程图见图2。图中的外层迭代过程用{F}(k)根据式(6)计算出等效的接触变形柔度矩阵[λc].将原非线性方程组(3)转换为线性方程组,通过判断前后两次载荷的差异判定是否收敛。内层迭代过程去除了未知变量{Y}的影响,由于参与接触的各点载荷均大于0,若{F′}中存在载荷小于0的值,则说明该点未参与接触,将对应的柔度矩阵[λ]和误差向量{ε}中的行和列划去,重新求解新的方程组,直至{F′}中所有载荷均大于 0,得到内层迭代的收敛解{F}(k+1)和δ(k+1)。算例结果表明,外、内层迭代一般均在5次内就能达到收敛,有效提高了求解效率。

图2 接触方程迭代求解流程Fig.2 Iteration scheme of solving the contact equations
得到载荷分布{F}和传递误差δ后,就可以计算齿轮副啮合刚度和综合啮合误差。齿轮副啮合刚度为各对接触点刚度之和。单对接触点对应的等效弹簧系统示意图如图3所示。由图中的变形关系可得齿轮副综合啮合刚度为


图3 单对接触点变形关系Fig.3 Deformation relationship of a contact pair
与单个接触点的变形关系类似,齿轮副综合啮合误差为传递误差δ与齿轮副综合变形Δ之差,即:
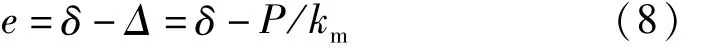
显然,当载荷较小时,齿面只有部分接触点参与啮合,实际啮合刚度会小于理想齿轮副刚度。只有当载荷增加至齿面实现完全接触时,实际啮合刚度才会与理想齿轮副刚度相等,综合啮合误差才能达到稳定。
2 啮合冲击力
由于轮齿弹性变形和误差的存在,主、从动齿轮的实际啮合基节会不相等,使得轮齿实际啮合点在进入啮合和退出啮合时会偏离理论啮合线,导致主从动齿轮产生瞬时速度差,引起线外啮合冲击力。啮合冲击包括啮入冲击和啮出冲击两种,其中啮入冲击力一般要明显大于啮出冲击力[9],因此本文仅考虑啮入冲击的影响。在轮齿进入啮合时,主从动轮实际基节之差可以用“啮合合成基节误差”Δfpbe表示,其大小为齿轮副相对变形量Δ与基节偏差Δfpb之和,即:

基节偏差Δfpb的大小主要与齿距偏差有关,同时受到齿廓偏差的影响。由于本文重点讨论齿廓偏差对系统振动的影响,所以不考虑齿距偏差引起的基节偏差量。对于如图4所示的某齿廓偏差曲线,在某一时刻t时由齿廓偏差引起的等效基节偏差量为:

式中,T为啮合周期,Fα(t)和 Fα(t+T)分别为 t时刻和t+T时刻的法向齿廓偏差值。
求得“啮合合成基节误差”后,根据相关几何关系可求得实际啮入点和两齿轮瞬时相对速度Δv[10]。根据冲击动力学相关理论,可得最大冲击力Fs为[10]:

图4 由齿廓偏差引起的等效基节偏差Fig.4 Equivalent normal pitch error due to profile deviation
式中:mred为齿轮副系统的等效质量;J1、J2分别为主、从动齿轮的转动惯量;ks为齿轮在初始啮入点的啮合刚度;rb1、rb2分别为主、从动齿轮的基圆半径。
由冲量定理可知,冲击作用时间为

假设冲击力为一半正弦脉冲,则冲击力函数fs(t)为

式中:ωc=π/tc为半正弦波的角频率。
3 动力学建模
在不考虑齿面摩擦的情况下,直齿轮副弯扭耦合动力学模型如图5所示。图中下标1表示主动轮,下标2表示从动轮。

图5 直齿轮副相对位移模型Fig.5 The relative displacement of a spur gear pair
将图5中各齿轮振动位移向啮合线方向投影,可得啮合线相对总变形为

式中:xi,yi,θi(i=1,2)分别为齿轮 i在横向和扭转方向的振动位移;α为啮合角;rbi(i=1,2)为齿轮 i基圆半径;e(t)为时变的法向综合啮合误差,可在第1节中计算得到;角度φ=α-,为从动轮安装相位。
根据牛顿第二定律,可得系统运动微分方程组为

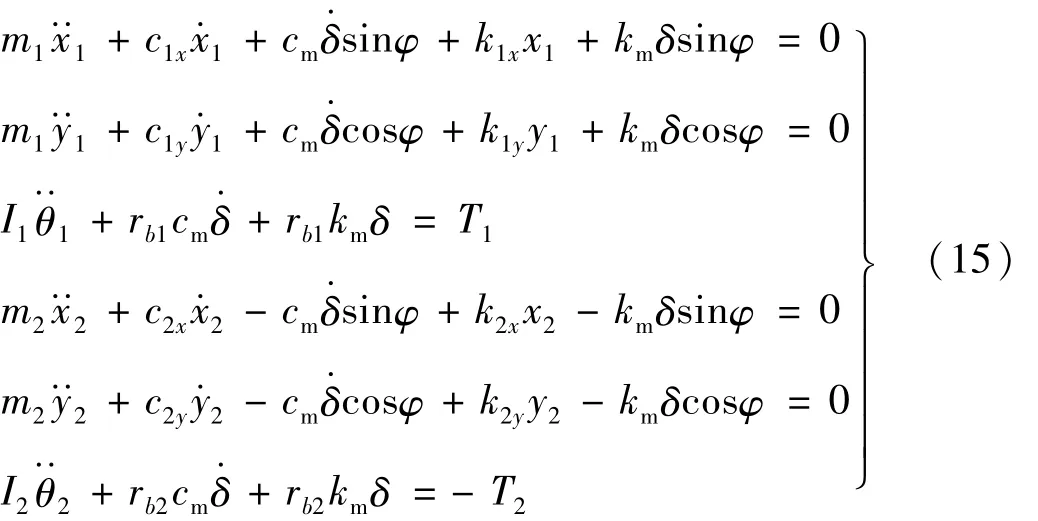
式中:mi,Ii(i=1,2)分别为齿轮 i的质量和转动惯量;km和cm分别为综合啮合刚度和啮合阻尼;kix,kiy,cix,ciy分别为齿轮i沿x向和y向的支撑刚度和阻尼;T1和T2分别为齿轮1和齿轮2的扭矩。
将式(14)代入方程组(15)中,并加入冲击力后整理成矩阵形式为:

式中:M,C和K分别为系统质量矩阵、阻尼矩阵和刚度矩阵;X为系统动态位移列向量,即动态传递误差;Ke和Ce·为啮合误差引起的系统自激振力向量;Fs为啮入冲击力在各自由度的分量。

由于动态位移波动ΔX是未知的,用静态传递误差波动ΔXs近似代替式(17)第二式右端的ΔX,则有

式中:FTE和Fs分别为传递误差激振力和冲击激振力。
这样式(16)中的参变微分方程组就变为式(18)所示的定常微分方程组,时变啮合刚度的影响被作为刚度激振力放在方程右端,能够避免使用数值积分方法求解。本文使用傅里叶级数法[12]直接求解方程(18)的稳态解ΔX,进一步得到系统位移响应X。
4 齿廓偏差类型对振动的影响
4.1 齿廓偏差参数描述
分析直齿轮副的基本参数如表1所示。

表1 分析齿轮副基本参数Tab.1 Basic paramters of the analyzed gear pair
为了分析不同形式齿廓偏差对直齿轮副振动的影响,假设齿廓偏差按以下五种形式变化,分别为理想齿廓、中凸齿廓、中凹齿廓、正压力角偏差齿廓和负压力角偏差齿廓。由于大齿轮误差值一般要明显大于小齿轮误差值,参照GB/T 3480-1997中计算动载系数的作法,仅以大齿轮误差代入计算模型。各类型齿廓偏差的示意图如图6所示,其中正、负压力角偏差以直线形式变化,中凸、中凹偏差以抛物线形式变化。假设各类型齿廓偏差具有相同的幅值Fα=5μm,则根据式(10)可得由齿廓偏差引起的等效基节偏差如表2所示。由于正、负压力角偏差齿廓曲线对称,所以两者具有相同的等效基节偏差但符号相反;对于中凸和中凹齿廓同样如此。
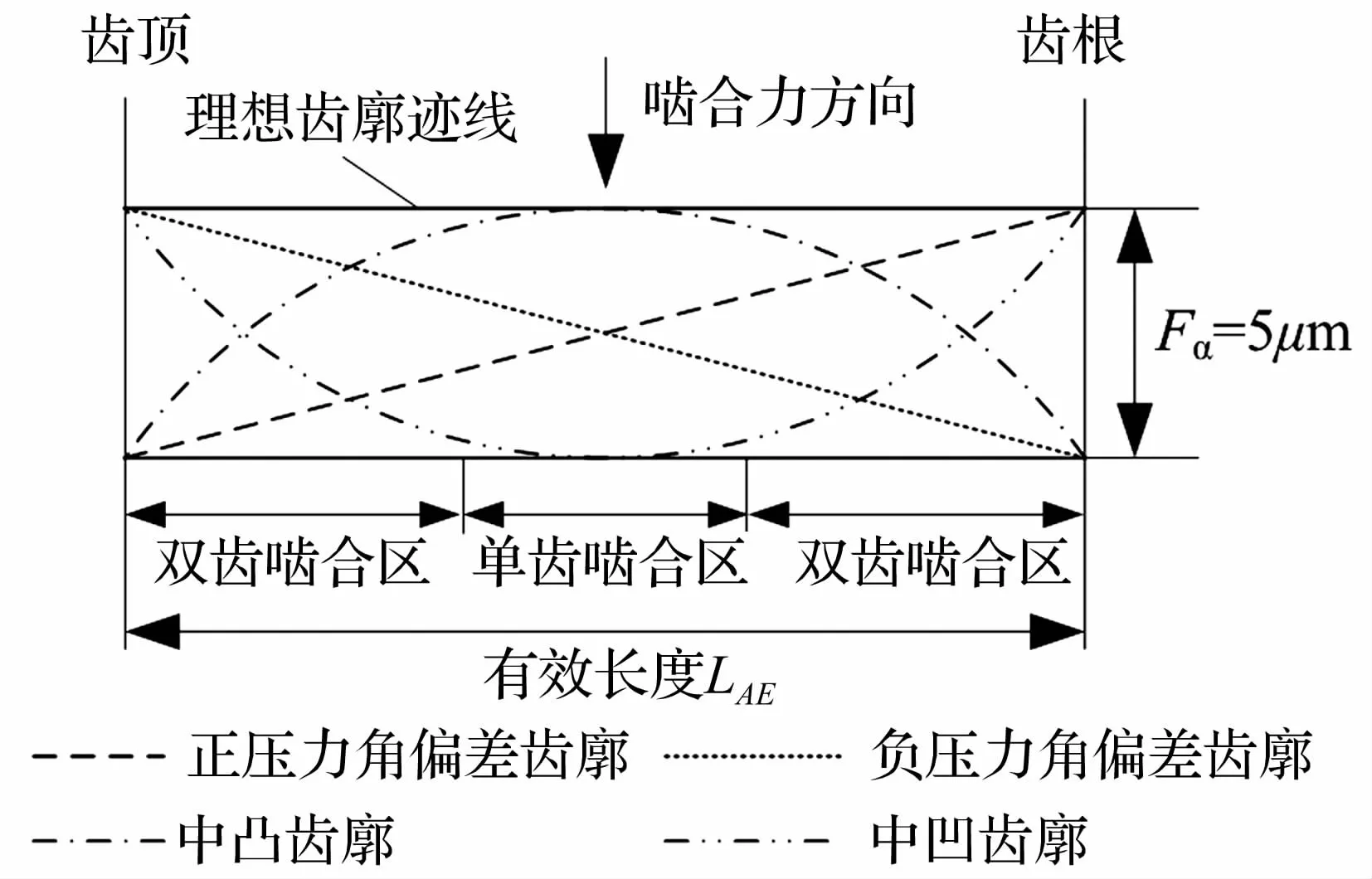
图6 各类型齿廓偏差示意图Fig.6 Schematic diagram for different profile deviations

表2 不同齿廓偏差对应的等效基节偏差Tab.2 Equivalent pitch errors for different profile deviations
4.2 不同齿廓偏差在相同负载下的系统响应
当负载扭矩为2 000 N·m时,具有不同类型齿廓偏差的齿轮副动载荷波动量随输入转速的变化情况如图7所示。由图7可以看出,随着转速的提高,各类型齿廓偏差对应的动载荷均在1 500 r/min和3 000 r/min左右出现峰值,这两个转速分别对应系统二次谐波共振和主共振转速。另外,在多数转速下对应于不同齿廓偏差类型的动载荷波动量从大到小的顺序为:中凹齿廓>负压力角偏差齿廓>正压力角偏差齿廓>理想齿廓>中凸齿廓。为了便于分析出现这种现象的原因,图8给出了转速为2 000 r/min时不同齿廓偏差所对应的传递误差激振力波动值和啮入冲击力大小。

图7 不同转速下的动载荷波动量Fig.7 Fluctuations of dynamic mesh forces at different speeds
对比图7与图8可以发现,各类型齿廓偏差对应动载荷大小排序与传递误差激振力的大小排序完全相同。对于中凸齿廓的齿轮,其效果类似于对齿廓进行起鼓修形,这样双齿啮合区的传递误差会增加,单齿啮合区的传递误差基本不变,而总体上使得传递误差波动值会有所减小,甚至小于理想齿廓的传递误差波动值,所以对应的传递误差激振力也最小。对于负压力角偏差和正压力角偏差的齿轮,在某一啮合时刻两者的误差呈对称分布,所以两者的传递误差激振力相差不大。而对于中凹齿廓的齿轮,误差的作用效果与中凸齿廓刚好相反,使得齿轮副具有最大的传递误差波动量及激振力。

图8 转速为2 000 r/min时各项激振力对比Fig.8 Comparison of exciting forces at 2 000 r/min
另外,由式(10)和表2可知,中凹齿廓和负压力角偏差齿廓会使“啮合合成基节误差”增加,因此两者对应的啮合冲击力将大于理想齿廓齿轮,如图8所示。而正压力角偏差和中凸齿廓均使齿顶减薄,“啮合合成基节误差”会减小,啮入冲击力随之减小。
综合对比两类激振力大小关系可以得到:中凹齿廓的总激振力最大,因此对应的动载荷最大;负压力角偏差齿廓的动载荷次之;中凸齿廓的动载荷最小。虽然正压力角偏差与理想齿轮的冲击力差值要明显大于两者的传递误差激振力差值,但由于冲击力的作用时间较短,所以理想齿轮的动载荷仍略小于正压力角偏差齿轮的动载荷,这也从侧面说明此时传递误差的影响要强于啮合冲击的影响。
4.3 不同齿廓偏差在不同负载下的系统响应
选取输入转速为4 000 r/min,不同齿廓偏差对应的动载荷波动量随负载扭矩T的变化曲线如图9所示。从图中可以看出,各类型齿廓偏差对应振动的相对大小关系在不同扭矩时会发生变化。为了便于分析原因,图10和图11分别给出了不同扭矩下各类型齿廓偏差所对应的传递误差激振力和冲击激振力。
从图9~图11中可以看出以下几点规律:
(1)理想齿廓的动载荷与扭矩近似呈线性关系变化。由于理想齿廓的传递误差与齿轮副变形相等,而齿轮副变形与载荷大小近似呈线性变化,所以传递误差激振力基本随载荷呈线性变化。与此同时理想齿廓的冲击激振力随载荷单调增加。两项激振力的综合效果使理想齿廓的动载荷随扭矩呈近似线性变化。
(2)中凹齿廓的动载荷在所有扭矩下均为各类型偏差中最大的。这是因为中凹齿廓的传递误差激振力(图10)和冲击激振力(图11)均为最大,这与4.2节的分析结论相一致。

图9 不同扭矩下的动载荷波动量Fig.9 Fluctuations of dynamic mesh forces at different torques

图10 不同扭矩下的传递误差激励力Fig.10 Exciting forces due to transmission error at different torques

图11 不同扭矩下的冲击激励力Fig.11 Impact forcesat different torques
(3)中凸齿廓在轻载(T=300N·m)时虽然无冲击激振力,但由于其传递误差激振力大于理想齿廓,所以导致此时中凸齿廓的振动要大于理想齿廓。这说明轻载时传递误差的影响要大于冲击的影响。当扭矩大于或等于600 N·m后,中凸齿廓的两类激振力都要小于理想齿廓,所以其振动也明显小于理想齿廓。这与文献[5]的试验结果完全吻合。
(4)正压力角偏差齿廓在T<2 400 N·m时的动载荷均大于理想齿廓,但在T≥2 400 N·m时,正压力角偏差齿廓的动载荷与理想齿廓基本相等,并将随着扭矩的继续增加而小于理想齿廓。由于正压力角偏差齿廓的传递误差激振力在所有扭矩下均大于理想齿廓,而理想齿廓的冲击激振力要大于正压力角偏差齿廓,这进一步说明冲击力在轻载时的影响要小于传递误差的影响,而在重载时的影响要大于传递误差的影响。
(5)负压力角偏差齿廓在T<900 N·m时的振动要小于正压力角偏差齿廓,但在T≥900 N·m时的振动要大于正压力角偏差齿廓。出现这种现象的原因为当扭矩较小时,负压力角偏差齿轮的传递误差激振力要小于正压力角偏差齿轮的数值,虽然此时负压力角偏差齿轮的冲击力明显大于正压力角偏差齿轮的冲击力,但由于轻载时冲击力影响较小,所以负压力角偏差齿轮的振动在轻载时仍小于正压力角偏差齿轮。而当扭矩较大时(T≥900 N·m),负压力角偏差齿轮的传递误差激振力和冲击激振力都将大于正压力角偏差的数值,所以其振动也大于正压力角偏差齿轮。
(6)从图10曲线中可以看出,当齿面存在误差时,在某一临界扭矩之前,传递误差激振力呈现不规则波动,而在该扭矩之后,传递误差激振力基本随扭矩呈线性变化,且与理想齿廓的曲线变化率基本一致。这是因为在临界扭矩之前,齿面仅有部分接触点实现啮合,齿轮副实际重合度小于理论重合度,导致相应的啮合刚度减小,综合啮合误差和传递误差曲线形状随扭矩改变而变化。当扭矩大于临界扭矩后,啮合力足以使所有接触点实现接触,此时齿轮副啮合刚度与无误差齿轮啮合刚度基本相等,综合啮合误差曲线不再改变;此时由齿面误差产生的激振力随扭矩基本不变,而由于啮合刚度产生弹性变形的激振力随扭矩呈线性变化,使得传递误差激振力随扭矩也呈近似线性变化。对于中凹齿廓、中凸齿廓、正压力角偏差齿廓和负压力角偏差齿廓,使齿面实现完全接触的临界扭矩分别为1 500 N·m、2 400 N·m、900 N·m和900 N·m左右。
5 结 论
(1)在轻载条件下,理想齿廓齿轮的振动最小;在中等载荷和重载时,具有中凸齿廓齿轮的振动最小。
(2)中凹齿廓齿轮在任何载荷状况下均具有最大的振动,负压力角偏差齿廓的齿轮在多数载荷情况下的振动仅次于中凹齿廓齿轮。
(3)正压力角偏差齿廓的齿轮在轻载及中等载荷条件下的振动要大于理想齿廓,但在重载条件时的振动逐渐减小并将小于理想齿廓齿轮。
(4)在轻载条件时,传递误差是系统最主要的激励成分;随着载荷的增加,啮合冲击所占的激励成分逐渐增加。
(5)在齿轮实际加工过程中,应避免出现中凹齿廓。对于从动轮,同时应避免负压力角偏差齿廓。
以上分析结果均是在误差齿轮作为从动轮的条件下得出的,当主、从动关系发生改变时,正、负压力角偏差的影响会出现正好相反的结论。
[1]李润方,陶泽光,林腾蛟,等.齿轮啮合内部动态激励数值模拟[J].机械传动,2001,25(2):1-4.LI Run-fang, TAO Ze-guang, LIN Teng-jiao, et al.Numerical simulation for inner dynamic excitation of gearing[J].Mechanical Transmission,2001,25(2):1-4.
[2]林腾蛟,蒋仁科,李润方,等.船用齿轮箱动态响应及抗冲击性能数值仿真[J].振动与冲击,2007,26(12):14-17.LIN Teng-jiao, JIANG Ren-ke, LI Run-fang, et al.Numerical simulation of dynamic response and shock resistance of marine gearbox[J].Journal of Vibration and Shock,2007,26(12):14-17.
[3]韩静波,刘更,吴立言,等.齿轮系统动力学误差激励合成方法研究[J].机械传动,2009,33(5):24-26.HAN Jing-bo,LIU Geng,WU Li-yan,et al.Study on method of synthesizing error excitation about gear system dynamics[J].Mechanical Transmission,2009,33(5):24-26.
[4]Matsumura S,Umezawa K,Houjoh H.Rotational vibration of a helical gear pair having tooth surface deviation during transmission of light load(4th Report,effect of tooth profile deviation)[J].Bulletin of JSME,1996,62(603):4324-4331.
[5]李凯岭,孙乃坤,崔剑平,等.渐开线齿轮不同形式齿廓偏差对齿轮噪声的影响[J].机械工程学报,2008,44(3):234-240.LI Kai-ling,SUN Nai-kun,CUI Jian-ping,et al.Influence on gear mesh noise from different tooth profile errors of involute gears[J]. Chinese Journal of Mechanical Engineering,2008,44(3):234-240.
[6]Li Shu-ting.Finite element analyses for contact strength and bending strength of a pair of spur gears with machining errors,assembly errors and tooth modifications[J].Mechanism and Machine Theory,2007,42(1):88-114.
[7]Rincon A F D,Viadero F,Iglesias M,et al.A model for the study of meshing stiffness in spur gear transmissions[J].Mechanism and Machine Theory,2013,61(3):30-58.
[8]丁长安,张雷,周福章,等.线接触弹性接触变形的解析算法[J].摩擦学学报,2001,21(2):135-138.DING Chang-an, ZHANG Lei, ZHOU Fu-zhang, et al.Theoretical formula for calculation of line-contact elastic contact deformation[J].Tribology,2001,21(2):135-138.
[9]李润方,王建军.齿轮系统动力学[M].北京:科学出版社,1996.
[10]周长江,唐进元,钟志华.齿轮传动的线外啮合与冲击摩擦[J].机械工程学报,2008,44(3):75-81.ZHOU Chang-jiang, TANG Jin-yuan, ZHONG Zhi-hua.Corner contact andimpact friction of gear drive[J].Chinese Journal of Mechanical Engineering,2008,44(3):75-81.
[11]张金梅,刘更,周建星,等.考虑啮入冲击作用下减速器的振动噪声分析[J].振动与冲击,2013,32(13):118-122.ZHANG Jin-mei, LIU Geng, ZHOU Jian-xing, et al.Vibration and noise radiation analysis for a gear reducer considering meshing impact[J].Journal of Vibration and Shock,2013,32(13):118-122.
[12]方宗德,沈允文,高向群.斜齿轮传动的动态特性分析[J].航空学报,1992,13(2):32-39.FANG Zong-de, SHEN Yun-wen, GAO Xiang-qun.An analysis of dynamic behaviour of helical gear transmissions[J].Acta Aeronautica et Astronautica Sinica,1992,13(2):32-39.
