基底隔震储液罐的参数动力稳定性分析及隔震效果评价

杨宏康，高博青

（1．浙江大学 空间结构研究中心，杭州 310058；2．碧桂园物业发展有限公司，广东 佛山 528312）

大型立式圆柱形储液罐主要用于储存石油、液化天然气（LNG）等能源，一旦发生震害破坏，后果十分严重。储液罐的抗震设计在Alaska地震以后开始以反应谱理论为基础，但在此之后，储液罐的震害破坏事故仍不断发生［1］。以刚度和延性抵抗地震的传统抗震方法，并不能完全满足储液罐的抗震安全性要求。

储液罐的基底隔震自上世纪90年代起开始引起关注。Kim等［2］对储液罐的足尺模型进行拟动力试验，结果表明叠层橡胶支座可显著减小基底剪力。De Angelis等［3］对外浮顶罐的缩尺模型进行振动台试验，发现高阻尼橡胶支座（HDRB）和塑料 －金属支座（SIEPD）均可显著减小脉冲压力，但会加大对流压力。Shrimali等［4］、Panchal等［5］以 Haroun模型为基础建立隔震储罐的质量弹簧模型，发现摩擦摆支座的隔震效果稍优于橡胶支座，且不会加剧对流效应。孙建刚等［6］则基于质量弹簧模型建立了基底隔震储液罐的基本分析理论。Shekari等［7］结合有限元与边界元法建立隔震储罐的数值模型，发现长周期地震对中等高径比的罐体影响更大。基底隔震技术在大型储液罐中的工程实践集中于LNG储罐，隔震器均匀布置在桩基础与混凝土承台间［8－9］。

储液罐易发生参数共振形式的动力失稳［10－11］，震害调查显示其在地震下易发生屈曲破坏［1］。减震措施若设置不当，甚至会加剧结构发生动力失稳［12］。前述研究者多采用质量弹簧模型模拟隔震储罐，大都以基底剪力、弯矩的减小程度评价减震效果，隔震措施对储液罐动力稳定性能的影响尚未引起足够重视。

本文将在文献［13］的基础上，由位移－压力格式的流固耦合模型建立隔震储液罐的周期系数扰动方程，以某160 000 m3LNG储罐为对象，基于Floquet理论对隔震前后的储罐进行动力稳定性分析，研究静液压、加强圈、隔震器参数对储液罐动力稳定性能的影响。

1 基本理论

1.1 位移－压力格式的流固耦合模型

一般储液罐的参数动力稳定性理论参见文献［13］，将隔震器简化为弹簧和阻尼元件，忽略隔震器质量［14］，则基底隔震储液罐的动力问题可表述为下述“位移－压力”格式的流固耦合有限元方程［15］：

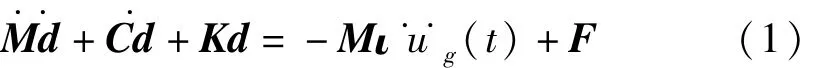
式中：

Ms0、Ks0、Cs0分别为自由状态下的结构域质量、刚度、阻尼矩阵；S、H、Cf分别为流体域的质量、刚度、阻尼矩阵；Q为耦合矩阵，ρf为流体密度，u为结构位移向量，p为流体压力向量，ub表示与隔震器相连的节点位移向量，ua为其余节点位移向量；Kb、Cb分别为隔震层的刚度矩阵和阻尼矩阵，Kb，n为ub的自由度数，kbi、cbi分别为隔震器在相应自由度方向的刚度和阻尼系数；ι为地震影响向量ιf分别与u、p对应，为地震加速度；FT＝｛GT，，G为静液压等静力作用的结构域节点力列阵。

基底隔震导致对流运动加剧的现象在短周期地震下并不显著［4，7］。假定储液为理想流体，忽略边界辐射和自由表面波动，凝聚压力自由度p，由式（1）建立下述等效结构域系统的动力方程［13］：

式中：Ma＝Ms＋Mu，Mu＝ρ0QH－1QT。H仅与流体域有关，Q受耦合界面特性控制，隔震器不会改变耦合界面特性，Mu不受基底隔震影响。

1.2 基于Floquet理论的动力稳定性分析方法

以几何刚度矩阵K0考虑G的预应力效应，对式（2）表征的等效结构域系统进行模态分析。引入扰动变量＝αcosθt，以时变几何刚度矩阵）考

g虑结构域在动力作用下的应力刚（软）化效应，式（2）的动力稳定性转化为周期系数扰动方程（3）的零解稳定性［13］：

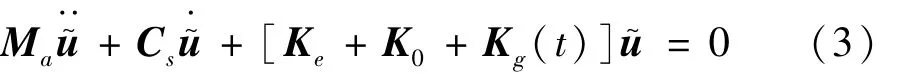
式中：为线弹性刚度矩阵；Si为第i阶主振型力下的几何刚度矩阵，阶次按有效振型质量排列，Si及i、k、βi、γi参见文献［13］；Cs0＝a0Ma＋a1（Ke＋K0），a0、a1为瑞利阻尼参数。按振型频率大小，选择前m阶振型列向量组成振型矩阵ψ，建议取 m∈［100，200］。利用 u～≈ψq将式（3）变换至振型坐标q，并改写为下述状态空间方程：

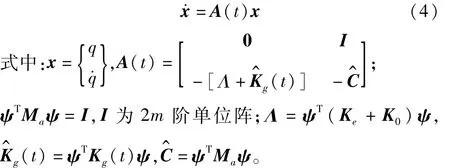
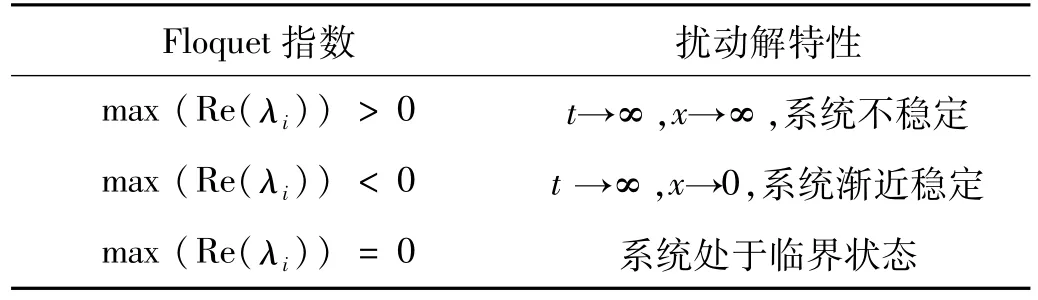
表1 参数动力失稳的判别准则Tab．1 Criterion for param etric dynamic instability

根据Floquet-Lyapunov定理，总存在常矩阵B使得X（t＋jT） ＝X（t）Bj（T＝2π／θ），X（t）为式（4）的基解矩阵。记B的特征值为ρi（i为特征值阶次），则Flo-quet指数 λi＝［ln｜ρi｜＋i arg（ρi）］／T。B不受初始扰动的影响，取 X（0）＝I2m，则 B＝X（T）。初始扰动xi（0）取为 I2m的第 i列向量，通过 Runge-Kutta法求解xi（T）和 X（T），按表 1判别储液罐在不同 α、θ下的动力稳定性，结果以动力不稳定域图的形式给出，纵轴为谐波加速度幅值 α，横轴为谐波频率 fθ，fθ＝θ／2π。

2 参数动力稳定性分析

2.1 模型参数

本文以160 000 m3全容LNG储罐的钢制内罐为分析对象［9］，几何参数如图1所示。全容式LNG储罐的钢制内罐和混凝土外罐间用珍珠岩与弹性毯填充，外罐不与储液直接接触，参考文献［16－17］的处理方式，针对钢制内罐进行分析。内罐壁共10层，t1～t10为各层壁厚，钢材弹性模量取206 GPa，泊松比取0．3；LNG密度取 462 kg／m3，体积弹性模量取 0．865 GPa［18］；为更符合实际构造，采用角钢L200×14（mm），分别在第6、8、10层壁板中部设置环向加强圈；当储液高度与第9层壁板顶平齐时，记为“满罐状态”；当储液高度与第5层壁板顶平齐时，记为“半罐状态”。

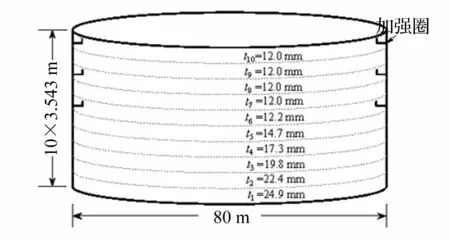
图1 160 000 m3 LNG储罐的钢制内罐Fig．1 Steel inner tank of160 000 m3 LNG storage tank

图2 储液罐的有限元模型Fig．2 Finite elementmodel of liquid storage tank

利用有限元软件ANSYS建立位移－压力格式的流固耦合模型，基于科学计算平台MATLAB，编写有限元模型数据接口，完成压力自由度凝聚及模态分析，并编制参数动力稳定性分析模块。罐壁和储液分别采用Shell 181和Fluid 30单元模拟，罐壁网格均匀划分为竖向20段和周向80段，流体网格与之协调；加强圈采用Beam 188单元模拟，网格与罐壁协调。考虑到C50混凝土承台对罐底的竖向加强，以Shell 181单元模拟底板，厚度取 1 m，弹性模量取 34．5 GPa，泊松比取 0．2。内罐常锚固于底部基础［17］，本文通过约束罐底的所有平动自由度来模拟内罐隔震前的边界条件。

LNG储罐按运行基准地震（OBE）和安全停运地震（SSE）进行抗震设计［19］，OBE、SSE的设防概率水准分别与GB 50011的中震、大震一致［20］。在已规划的LNG接收站中，设防烈度最大为唐山接收站的8°（0．20 g）［21］，相应的小、中、大震的加速度峰值分别为 0．7、2．0、4．0 m／s2［20］。同型号钢制内罐的几何参数相似，隔震结构可适当提高设防目标，故本文选择在α∈［0，4．0］m／s2的谐波幅值区间内，对图1所示的储液罐进行水平简谐地面加速度下的参数动力稳定性分析。

2.2 模态分析

已建隔震储罐多采用叠层橡胶支座和铅芯橡胶支座［8］。本文选择附加粘滞阻尼器的叠层橡胶支座作为隔震器［14］，隔震器均匀布置于罐底，以Combin 14单元模拟，取罐底有限元节点作为隔震器的均布布点。在笛卡尔坐标系o－xyz下，假定隔震器的z向刚度为无限大，记第i个隔震器在x、y向的刚度和阻尼系数分别

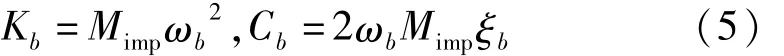
式中：ωb＝2π／Tb，Tb为结构整体隔震周期，ζb为隔震层整体阻尼比，Mimp为储液罐的脉冲质量。对等效结构域系统进行无阻尼模态分析，按排列振型阶次，第1阶主振型周期即储液罐的脉冲周期Timp；储液罐的振型较为密集，Mimp等于Timp所对应振型的之和。

表2 储液罐的动力特征参数Tab．2 Dynamic characteristic parameters of liquid storage tank

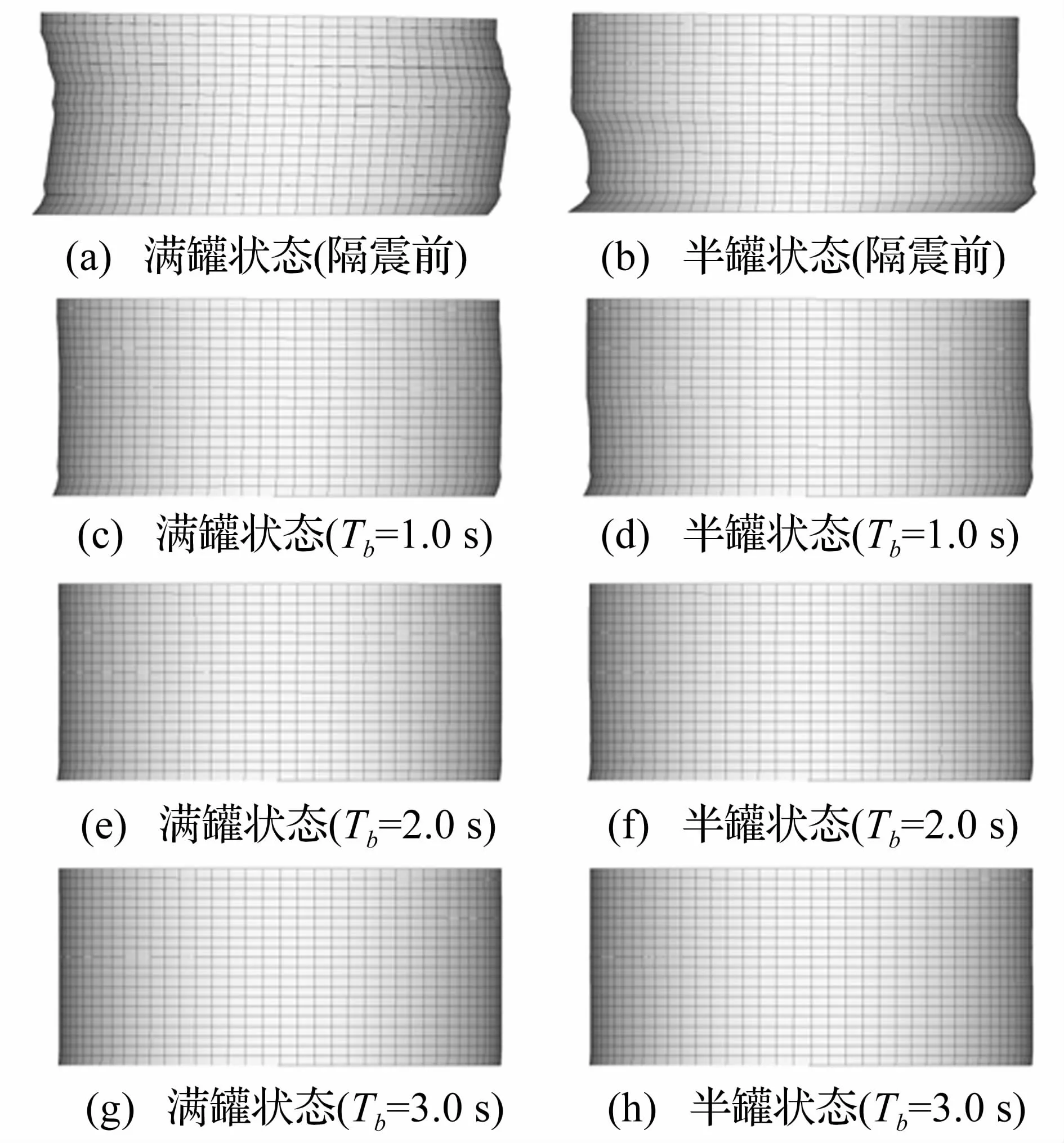
图3 储液罐的第1阶主振型Fig．3 First primarymode of liquid storage tank

针对隔震前的满罐状态进行隔震设计，每一布点均采用相同样式和相同参数的隔震器，按式（5）确定隔震器参数，分别取 Tb＝1．0、2．0、3．0 s，基于等效结构域系统进行模态分析，结果如表2和图3所示。在第1阶主振型下，罐壳截面保持圆形，故本文仅给出振型的立面图。由图3知，储罐隔震前的第1阶主振型基本符合梁式振动的特点，随着Tb的增大，隔震后的第1阶主振型逐渐转变为纯平动振型。由表2知，与隔震前储罐相比，隔震储罐的Mimp在满罐和半罐状态下分别增大约16%与28%，且隔震储罐的Mimp几乎不受Tb的影响。

2．3 静液压与加强圈的影响

静液压提供的预应力效应会影响储罐的振动特性，而加强圈设计通常仅基于静力稳定校核进行。选择 Tb＝1．0 s，ζb＝5%，按是否考虑静液压与加强圈，对隔震储液罐进行动力稳定性分析（取m＝150，下同），结果如图4所示，0．1 Hz表征储液晃动频率的界限。

图4 静液压与加强圈对隔震储液罐动力不稳定域的影响Fig．4 Influence of hydrostatic pressure and stiffening girder on dynamic instability regions of isolated liquid storage tank

考虑加强圈，按是否忽略静液压，由图4可知：

（1）忽略静液压时，在两种储液水平下，动力不稳定域均几乎铺满fθ－α平面；考虑静液压后，动力不稳定域的范围大幅减小，不稳定域的临界幅值增大。

（2）考虑静液压后，半罐状态储液罐的动力不稳定域范围比满罐状态略大；相比满罐状态，半罐状态储液罐的不稳定临界幅值更高，不稳定频段范围更大。

考虑静液压，按是否忽略加强圈，由图4可知：

（1）当忽略加强圈时，满罐状态储液罐的动力不稳定域位于0．47～1．13 Hz，0．44～4．00 m／s2的参数平面内，在考虑加强圈后，动力不稳定域小幅收缩至0．62～1．02 Hz，0．7～4．00 m／s2的范围内。

（2）当忽略加强圈时，半罐状态储液罐在0．42～4．00 Hz，0．49～4．00m／s2的参数平面内存在大片连续的动力不稳定域，在考虑加强圈后，动力不稳定域大幅缩小至1．08～1．65 Hz，1．34～4．00 m／s2的范围内。

（3）当忽略加强圈时，半罐状态储液罐比满罐状态更易发生参数动力失稳，而考虑加强圈影响后，满罐状态储液罐的动力稳定性能则略优于半罐状态。

图5 储液罐隔震前后的动力不稳定域对比Fig．5 Contrast of dynamic instability regions of liquid storage tank before and after isolation

考虑静液压与加强圈的影响，分别对隔震前后的储液罐进行参数动力稳定性分析，取 Tb＝1．0 s，ζb＝5%，结果如图5所示。按小、中、大震的加速度峰值水平将 α划分为小震幅段（0～0．7 m／s2）、小中震幅段（0．7～2．0 m／s2）和中大震幅段（2．0～4．0 m／s2）。由图5可知：

（1）满罐状态：在由下至上三个幅段内，隔震前动力不稳定域的相应频段为（1．81～2．29）、（1．70～3．85）、（1．29～3．96）Hz，频段范围呈增大趋势；隔震后，动力不稳定域被限制在（0．68～4．00）m／s2、（0．61～1．03）Hz的狭窄区域内，动力不稳定域向（1／Tb）Hz附近产生明显迁移，且已基本脱离小震幅段范围。

（2）半罐状态：在由下至上三个幅段内，隔震前动力不稳定域的相应频段为（3．16～3．63）、（2．75～4．75）、（2．36～5．00）Hz；隔震后的不稳定域迁移至（1．34～4．00）m／s2、（1．08～1．66）Hz的区间内，已完全脱离小震幅段。

（3）在隔震前后，半罐状态的动力不稳定域面积均比满罐状态略大；隔震后，相比满罐状态，半罐状态的动力不稳定域临界幅值更大，距离隔震前的动力不稳定域更远。隔震措施有益于缓解储罐的参激动力失稳现象，且半罐状态下的缓解效果更优。

静液压提供的环向拉应力有益于“刚化”壳体，动液压使壳体在竖向处于往复拉压状态，压应力会“软化”壳体。储液深度同时影响静动液压的分布和大小，而加强圈能箍紧罐壁，有助于抑制环向多波振动。当同时考虑加强圈与静液压的影响时，半罐状态储液罐的动力稳定性比满罐状态略好。

2．4 隔震器参数的影响

选择 Tb＝1．0、2．0、3．0 s，隔震储液罐的参数动力稳定性分析结果如图6所示，其中，5%、10%、15%分别表示不同的隔震层阻尼比ζb。主要结论如下：

（1）满罐状态：随Tb的增大，隔震后的动力不稳定域均向（1／Tb）Hz附近迁移，频段范围减小，动力不稳定域变得“瘦长”；在不同Tb下，隔震后的动力不稳定域均得到有效控制，且随ζb的增大，不稳定域的临界幅值呈上升趋势。

（2）半罐状态：隔震后的动力不稳定域随Tb、ζb的变化趋势与满罐状态相似；当取 Tb＝2．0、3．0 s，ζb＝15%时，在图示参数范围内，动力不稳定域完全消失。

（3）在相同的隔震器参数下，满罐、半罐状态的动力不稳定域具有相近的频段宽度，但半罐状态的不稳定临界幅值更大；对比不同Tb下的动力不稳定域，Tb＝1．0 s时的不稳定边界特性最为复杂。

基于储液罐的参数动力稳定性分析结果，结合抗震设防要求，建议按如下原则进行隔震控制：① 在不同储液水平下，隔震前后的动力不稳定域应相互远离，不宜存在交叉、重叠现象；② 隔震后的动力不稳定域应呈“瘦长”型并控制在隔震储罐的脉冲频率（1／Timp）附近；③ 由于隔震结构可适当提高设防目标，故动力不稳定域的临界激励幅值应至少控制在中震幅值水平以上。综上，为满足参数动力稳定性要求，针对图1模型，本文建议取 Tb＝2．0 s或3．0 s，ζb＝15%。

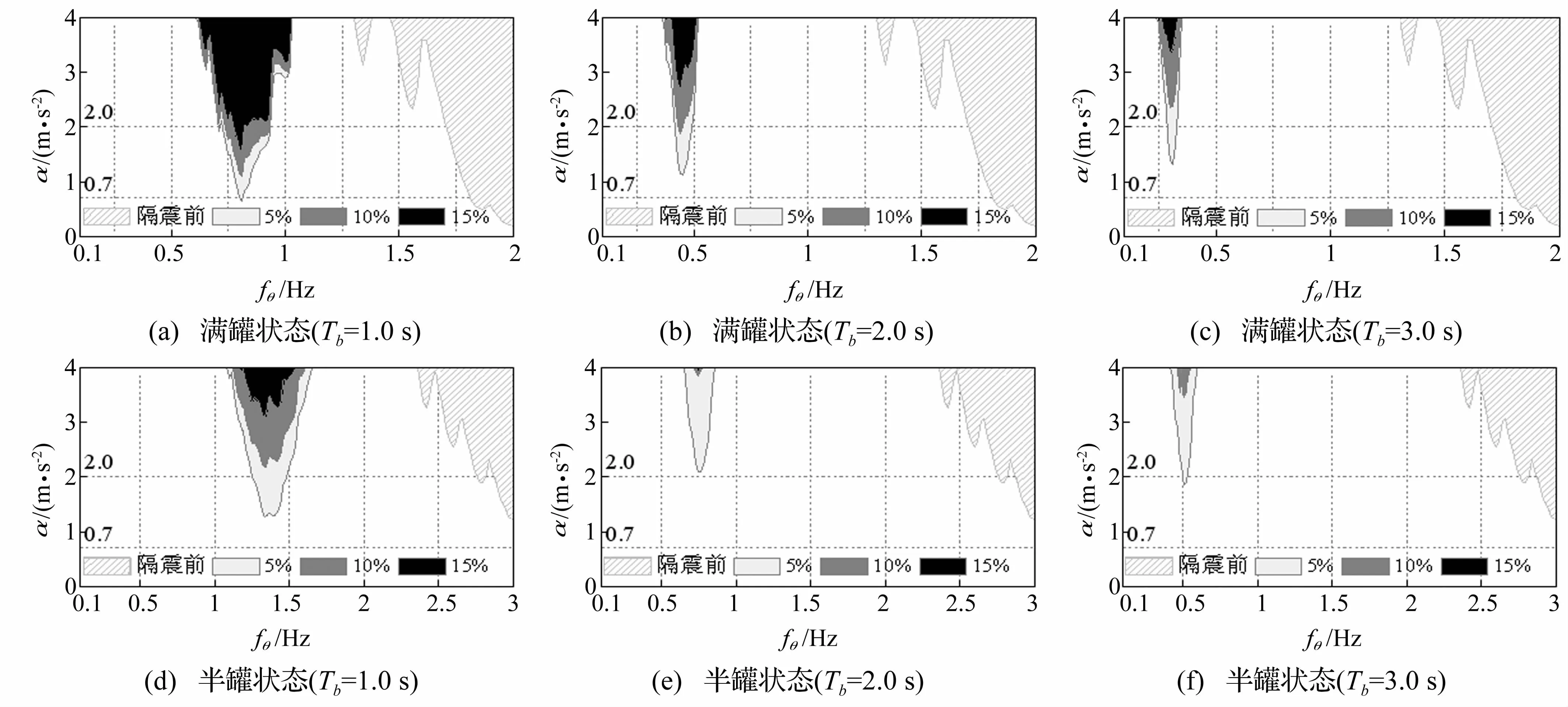
图6 储液罐在不同隔震参数下的动力不稳定域Fig．6 Dynamic instability regions of liquid storage tank with different isolation parameters

3 结 论

（1）通过凝聚流体域压力自由度，由位移－压力格式的流固耦合模型建立隔震储液罐的周期系数扰动方程，并基于Floquet理论求解参数动力不稳定域。

（2） 等效结构域系统的模态分析表明，基底隔震措施会加大储液在动力响应中的参与程度。在进行储罐的隔震设计时，需注意储液脉冲质量的变化。

（3）静液压提供的环向拉应力有助于刚化薄壁壳体并抑制参数动力失稳，而加强圈能箍紧罐壁，有助于抑制环向多波振动。当同时考虑加强圈与静液压时，半罐状态储液罐的动力稳定性能比满罐状态略好。

（4）随着隔震器刚度的减小，隔震储罐的动力不稳定域向低频段迁移；随着隔震器阻尼系数的增大，动力不稳定域的临界幅值呈上升趋势，且这种趋势在隔震储罐的脉冲频率附近更为显著。隔震器对动力不稳定域的抑制效果在半罐状态下更为显著。

（5）铅芯橡胶支座、摩擦摆支座等利用塑性或摩擦来耗散地震能量的隔震装置，阻尼机理更复杂，如何分析这类隔震器对储罐动力稳定性能的影响还需继续探索，本文方法可用于此类隔震器的初步复核。

［1］Cooper TW．A study of the performance of petroleum storage tanks during earthquakes，1933－1995［R］．Gaithersburg，MD：National Institute of Standards and Technology，1997．

［2］Kim N S，Lee D G．Pseudodynamic test for evaluation of seismic performance of base-isolated liquid storage tanks［J］．Engineering Structures，1995，17（3）：198－208．

［3］De Angelis M，Giannini R，Paolacci F．Experimental investigation on the seismic response of a steel liquid storage tank equipped with floating roof by shaking table tests［J］．Earthquake Engineering＆ Structural Dynamics，2010，39（4）：377－396．

［4］Shrimali M K，Jangid R S．A comparative study of performance of various isolation systems for liquid storage tanks［J］．International Journal of Structural Stability and Dynamics，2002，2（4）：573－591．

［5］Panchal V R，Jangid R S．Variable friction pendulum system for seismic isolation of liquid storage tanks［J］．Nuclear Engineering and Design，2008，238（6）：1304－1315．

［6］孙建刚，王向楠，赵长军．立式储罐基底隔震的基本理论［J］．哈尔滨工业大学学报，2010，42（4）：639－643．SUN Jian-gang， WANG Xiang-nan， ZHAO Chang-jun．Theoretical study on seismic isolation of storage tanks［J］．Journal of Harbin Institute of Technology，2010，42（4）：639－643．

［7］Shekari M R，Khaji N，Ahmadi M T．On the seismic behavior of cylindrical base-isolated liquid storage tanks excited by long-period groundmotions［J］．Soil Dynamics and Earthquake Engineering，2010，30（10）：968－980．

［8］Marti J，Crespo M，Martinez F．Seismic isolation of liquefied natural gas tanks：a compartive assessment［J］．Seismic Isolation and Protective Systems，2010，1（1）：125－140．

［9］黄淑女，王作乾．我国第一座16万m3全容LNG储罐［J］．石油工程建设．2009，35（4）：15－18．HUANG Shu-nv，WANG Zuo-qian．First 16×104 m3 full capacity LNG storage tank in China［J］． Petroleum Engineering Construction．2009，35（4）：15－18．

［10］Chiba M，Tani J，Hashimoto H，et al．Dynamic stability of liquid-filled cylindrical shells under horizontalexcitation，part I：experiment［J］．Journal of Sound and Vibration，1986，104（2）：301－319．

［11］Fukuyama M，Nakagawa M，Ishihama K，et al．Dynamic buckling experiments of fluid-structure-coupled co-axial thin cylinder［J］．Nuclear Engineering and Design，1999，188（1）：13－26．

［12］Bolotin V V．The dynamic stability of elastic systems［M］．San Francisco：Holdenday，1964：1－7．

［13］杨宏康，高博青．基于Floquet理论的储液罐动力稳定性分析 ［J］．浙江大学学报（工学版），2013，47（2）：378－384．YANG Hong-kang，GAO Bo-qing．Dynamic stability analysis of liquid storage tanks based on Floquet theory［J］．Journal of Zhejiang University（Engineering Science），2013，47（2）：378－384．

［14］Skinner R I，Robinson W H，Mcverry G H．工程隔震概论［M］．谢礼立等译．北京：地震出版社，1996：17－40．

［15］Moslemi M，Kianoush M R．Parametric study on dynamic behavior of cylindrical ground-supported tanks ［J］．Engineering Structures，2012，42：214－230．

［16］Cho JR，Lee JK，Song JM，etal．Free vibration analysis of aboveground LNG-storage tanks［J］．Journal of Mechanical Science and Technology，2000，14（6）：633－644．

［17］Christovasilis I P， Whittaker A S． Seismic analysis of conventional and isolated LNG tanks usingmechanical analogs［J］．Earthquake Spectra，2008，24（3）：599－616．

［18］Syahruddin N．LNG loading lines surge analysis for ESD system application［C］／／Proceedings of the International MultiConference of Engineers and Computer Scientists 2011．HongKong：IMECS，2011：1231－1236．

［19］GB／T 26978－2011现场组装立式圆筒平底钢制液化天然气储罐的设计与建造 ［S］．北京：中国标准出版社，2011．

［20］GB50011－2010建筑抗震设计规范［S］．北京：中国建筑工业出版社，2010．

［21］李健胡．美日中LNG接收站建设综述［J］．天然气技术，2010，4（2）：67－71．LI Jian-hu． A summary of LNG receiving terminal construction in USA，Japan and China［J］．Natural Gas Technology，2010，4（2）：67－71．