基于三维参数化建模的翼柱形发动机药形优化①

张维星，唐国金

(国防科技大学航天科学与工程学院，长沙 410073)

基于三维参数化建模的翼柱形发动机药形优化①

张维星，唐国金

(国防科技大学航天科学与工程学院，长沙 410073)

增大体积装填分数是提高固体火箭发动机总冲的重要手段之一，但这往往会导致药柱的应力和应变较大，影响其结构完整性。为了解决这一问题，提出了基于三维参数化建模和遗传算法的固体发动机药形优化设计方法。利用MSC.Patran的二次开发工具PCL(Patran Command Language)建立了某翼柱形发动机的参数化模型，并对温度、内压载荷联合作用下的药柱进行了几何参数灵敏度分析，在此基础上，利用遗传算法对该药柱进行了药形优化。在体积装填分数不减少的前提下，得到了最大Von Mises应变取极小值时所对应的最优药形。所提方法可用于多种固体火箭发动机的药形优化设计，对改善高装填分数条件下发动机的结构完整性具有一定的工程实用价值。

药形优化;结构完整性;体积装填分数;三维参数化建模;灵敏度分析;遗传算法

0 引言

提高固体发动机装填分数是实现新一代导弹武器大射程、高机动性的重要途径。然而装填分数高的药柱，其应力、应变一般也比较大，可能会导致发动机无法满足结构完整性的要求［1］。因此，为了设计出性能优良的发动机，必须在提高体积装填分数和降低药柱结构响应之间进行折衷，找到一种最优药形。

固体发动机的优化设计一直是国内外学者研究的重点。Raza等［2］针对双推力固体火箭发动机的车轮形药柱进行了研究，并提出一种综合计算机辅助设计技术(CAD)和混合优化理论的优化设计方法，使得推进段与保持段平均推力的比值以及发动机总冲最大;Ali Kamran等［3］利用CAD软件实现了三维伞盘形药柱的参数化建模，并基于遗传算法对其内弹道特性进行了优化，得到了发动机平均推力最大的药形;杨涓等［4］以燃烧室最大压强与平均压强之比作为目标函数，利用正交试验优化设计方法对固体发动机药柱进行了优化;窦毅芳等［5］将稳健优化方法引入了固体火箭发动机装药设计中，较好地解决了发动机推力不平衡的问题;王锟等［6］针对固体火箭发动机的特点，提出了基于数据库技术的结构优化设计方法。

到目前为止，发动机药形优化的研究主要集中在内弹道性能的提升上，而药柱结构完整性优化方面的成果还很少。其主要原因在于:对药柱进行结构完整性分析时，建模过程十分繁琐，且在优化过程中需要多次调用有限元程序重复建模，工作量特别大。李磊等［7-8］在药柱结构完整性的优化方面取得了一些研究成果，但其优化对象主要是二维轴对称模型，无法真实反映实际型号发动机复杂三维药形的力学行为。然而到目前为止，对于三维药柱结构完整性优化的研究成果还未见报道。

本文利用MSC.Patran/Marc的二次开发工具PCL，实现了翼柱形发动机的三维参数化建模。经过灵敏度分析后，确定与发动机结构完整性和体积装填分数密切相关的几何参数，并在此基础上利用遗传算法对该三维翼型药柱进行了优化设计。

1 发动机参数化建模

1.1 发动机模型

实际的翼柱形发动机构造复杂，为便于建模和计算，忽略喷管、点火器等结构以及一些工艺上的细节，建立以壳体、绝热层和药柱为主要部件的有限元模型。简化后的药柱模型从头至尾大体上可被划分为2段:圆管段和翼槽段。其中，翼槽段的12只大、小翼沿发动机环向均匀分布。

考虑燃烧室结构及载荷的循环对称性，沿发动机环向取整体的1/12建立有限元模型，如图1所示。该模型共生成单元38 444个，节点44 579个。

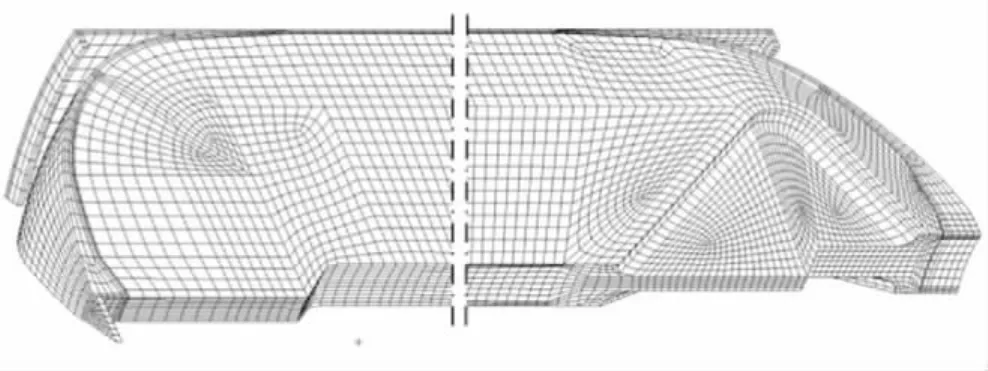
图1 发动机有限元模型Fig.1 Finite element model of SRM

图1中正面显示的翼槽为大翼槽，而背面是与大翼槽形状相似但尺寸偏小的小翼槽。药柱首尾的人工脱粘层裂缝尖端位置通常存在一定程度的应力集中，对这两处的网格进行了特殊的加密处理。

1.2 材料参数

发动机的壳体、绝热层和药柱分别采用不同的材料。其中，壳体为正交各向异性的复合材料，绝热层为线弹性材料，而药柱是粘弹性材料。三者的基本材料参数见表1所示。

对于壳体而言，由于是正交各向异性材料，因此需要分别定义与之相关的3个方向的弹性模量、线膨胀系数、泊松比和剪切模量，这些材料参数分别如表2和表3所示。

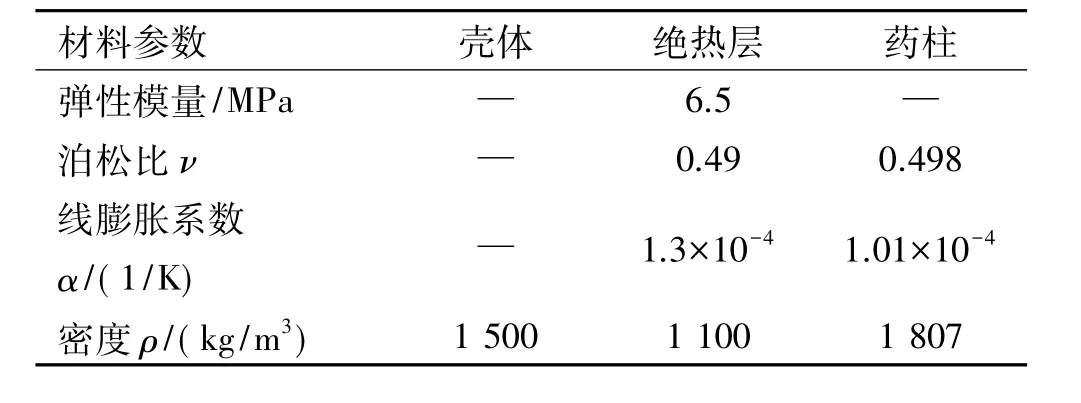
表1 发动机基本材料参数Table 1 Basic material parameters of SRM

表2 壳体的弹性模量和线膨胀系数Table 2 Elastic modulus and thermal expansion coefficient of the case

表3 壳体的泊松比和剪切模量Table 3 Poisson’s ratio and shear modulus of the case

在利用MSC.Patran定义壳体的材料属性时，需针对壳体的不同部位建立不同的坐标系。在这些局部坐标系下分别定义壳体各部分的材料属性，使几何结构的对称面与所定义的正交各向异性材料的对称面重合或者近似重合，以防止材料属性失真。

对于药柱而言，通过推进剂的单向拉伸试验得到拉伸松弛模量随时间的变化关系，即Prony级数:

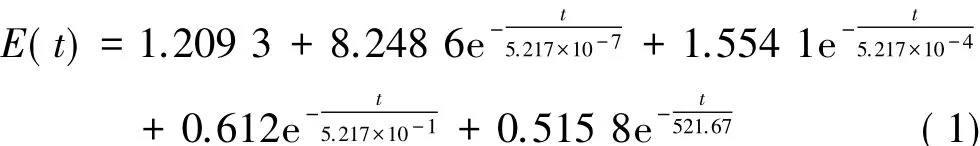
据此可得到药柱的初始模量E0=12.14 MPa。另外，利用WLF方程定义粘弹性药柱的时温等效特性:

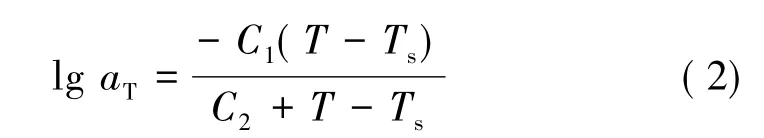
在参考温度Ts=20℃时，WLF方程的系数为:C1=10.6 和 C2=144.85。

1.3 载荷及边界条件

考虑常温环境下进行地面试车的过程，发动机先后经历了固化降温和点火试车两个工况。

固化降温时，假设在1 d时间内，推进剂温度由零应力温度58℃线性下降到室温20℃，且整个发动机为均匀温度场。固化降温结束后，对发动机进行点火试车，并假设其内压在0.3 s时达到最大值8.9 MPa。

1.4 结构完整性评估准则

在温度和内压联合载荷作用下，危险点位于药柱内表面，破坏准则采用八面体剪应变准则较为合理［9］。根据Marc软件的特点，本文采用与八面体剪应变准则等效的Von Mises应变准则来判断药柱的结构完整性。

1.5 基于PCL的参数化建模方法

利用PCL进行固体发动机参数化建模的基本流程［10］为:

(1)手动建立有限元模型;

(2)在日志文件中提取PCL语句，形成参数化建模的基本命令流，并对其进行整理;

(3)选择需要进行参数化的几何尺寸，将其申明为变量，把PCL程序中相关的数值用变量替代;

(4)编写网格数量控制程序，并添加结果提取和报告输出模块，即可形成一个比较完善的参数化建模程序。

本文选定与发动机大翼槽相关的8个参数作为设计变量，如图2所示，8个参数分别为:翼槽2条底边的长度L1、L2;翼槽2条侧边的长度L3、L4;翼槽顶部圆弧半径 r;3 个角度 α1、α2和 α3。

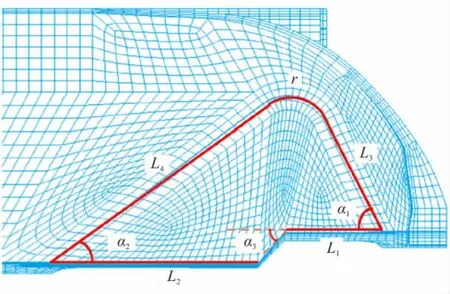
图2 药柱大翼槽结构示意图Fig.2 Sectional drawing of the large finocyl part of the grain

2 药柱几何参数灵敏度分析

上文所选定的8个几何参数对药柱结构响应和体积装填分数的影响规律各不相同，为衡量各个几何参数的重要程度，需要对其进行灵敏度分析。简单来说，灵敏度就是结构响应或体积装填分数对设计参数的变化率，即偏导数，灵敏度越高的参数对结构响应和体积装填分数的影响越剧烈。

本文采用中心差分法计算最大Von Mises应变和体积装填分数对几何参数的灵敏度系数。对于一个以x为自变量的函数f(x)，中心差分法的计算公式为

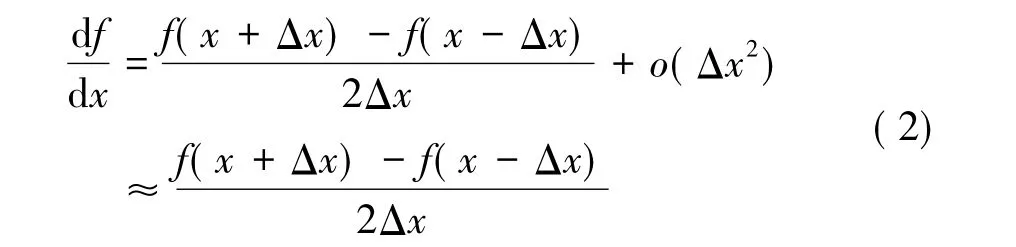
2.1 最大Von Mises应变对几何参数的灵敏度分析

当分析某个几何参数的灵敏度时，保持其他参数为默认值不变。由于各几何参数的变化范围差别较大，为便于比较，将几何参数与其默认值的比值作为无量纲值，用于计算灵敏度系数。

在联合载荷作用下，药柱的最大Von Mises应变εVmax随几何参数的变化规律见图3，利用式(2)计算得到εVmax对几何参数的灵敏度系数，其变化曲线如图4。

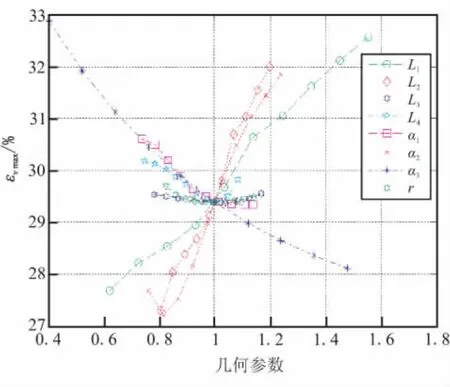
图3 εVmax随几何参数的变化规律Fig.3 εVmaxvariation with geometric parameters

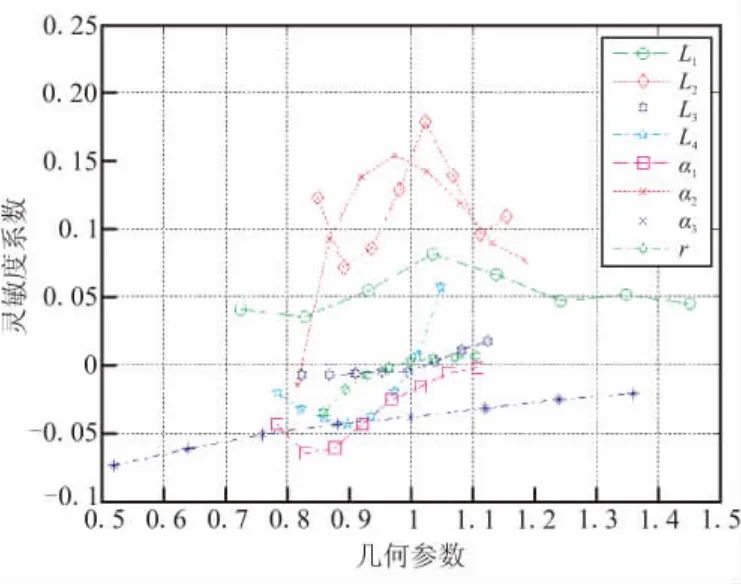
图4 εVmax对几何参数的灵敏度系数变化规律Fig.4 Curves of sensitivity coefficient vs geometric parameters for εVmax

数据分析后，将εVmax随几何参数的变化规律及灵敏度系数的变化范围总结在表4中。

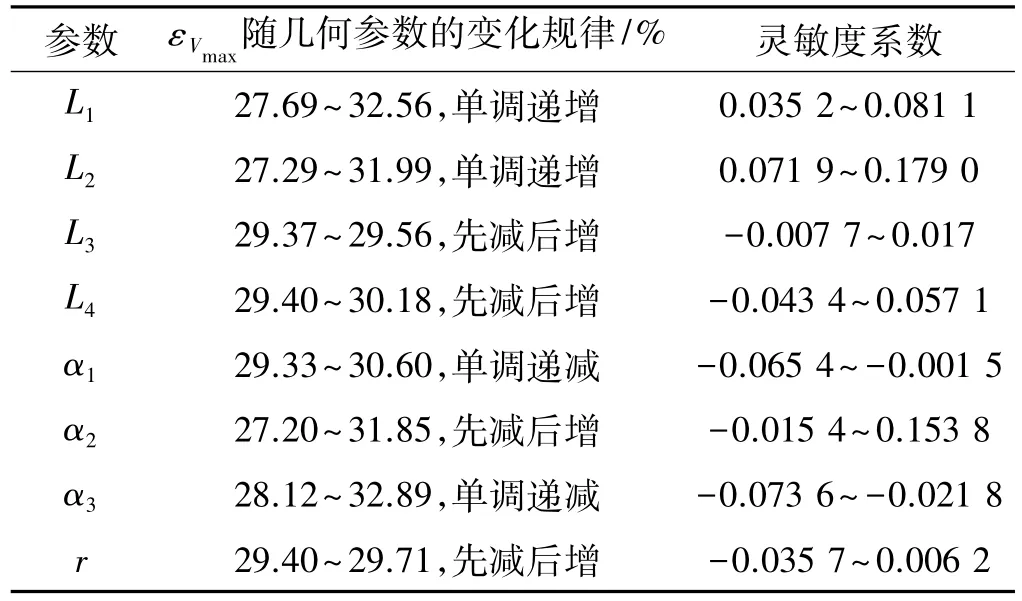
表4 εVmax对几何参数的灵敏度系数计算结果Table 4 Results of the geometric parameters sensitivity coefficient for εVmax

结果表明，在联合载荷作用下，药柱的εVmax随L1和L2的增大呈单调递增趋势;随L3、L4、α2和r的增大呈现先减小后增大的趋势，存在εVmax的极小值;随α1和α3的增大呈单调递减趋势。几何参数灵敏度由高到底的排序为:L2，α2，L1，α3，α1，L4，r，L3。

2.2 体积装填分数对几何参数的灵敏度分析

利用参数化建模程序提取出发动机药柱的体积装填分数ηV，ηV随几何参数的变化规律见图5。相比于最大应变εVmax，ηV随几何参数的变化曲线要规则很多，这主要是因为体积装填分数与几何参数之间是相对简单的非线性关系。同样利用式(3)计算得到体积装填分数对几何参数的灵敏度系数，并将其绘制成图6所示的曲线图。

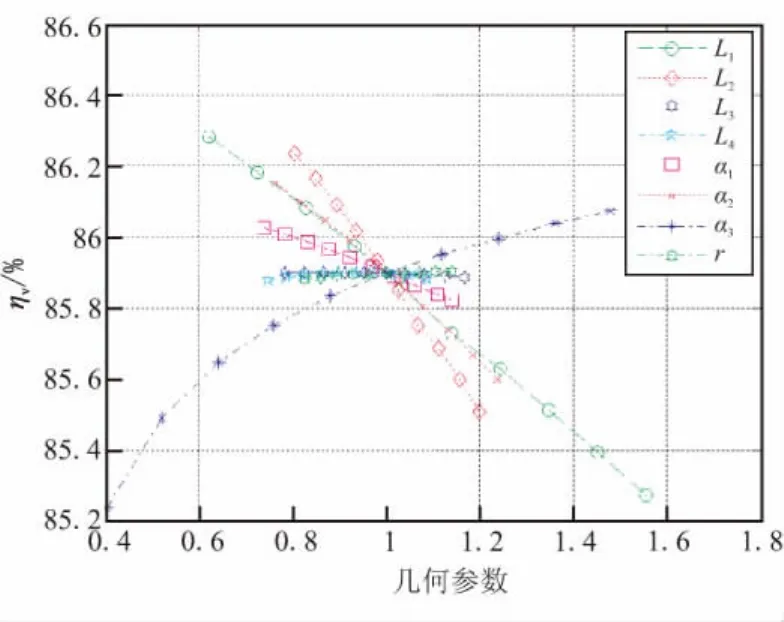
图5 ηV随几何参数的变化规律Fig.5 ηVvariation with geometric parameters

数据分析后，将ηV随几何参数的变化规律及灵敏度系数的变化范围总结在表5中。

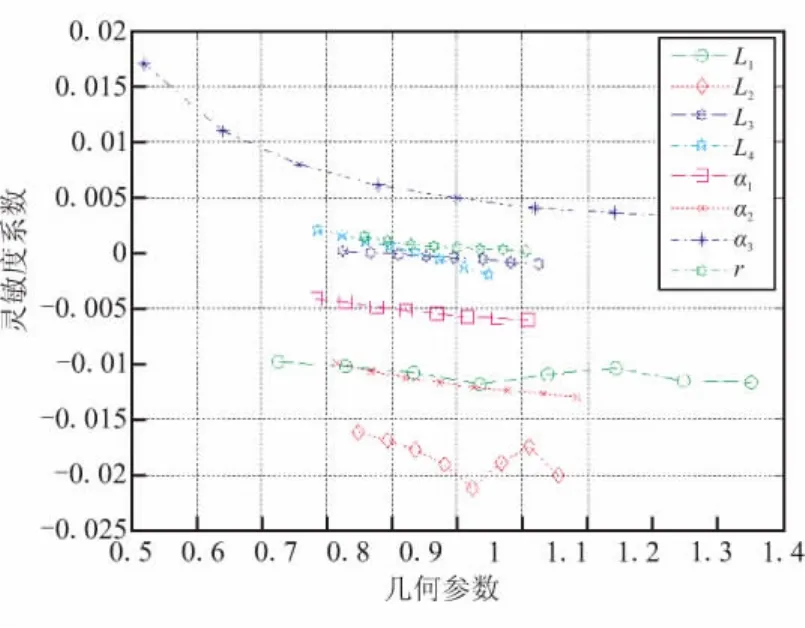
图6 ηV对几何参数的灵敏度系数变化规律Fig.6 Curves of sensitivity coefficient vs geometric parameters for ηV

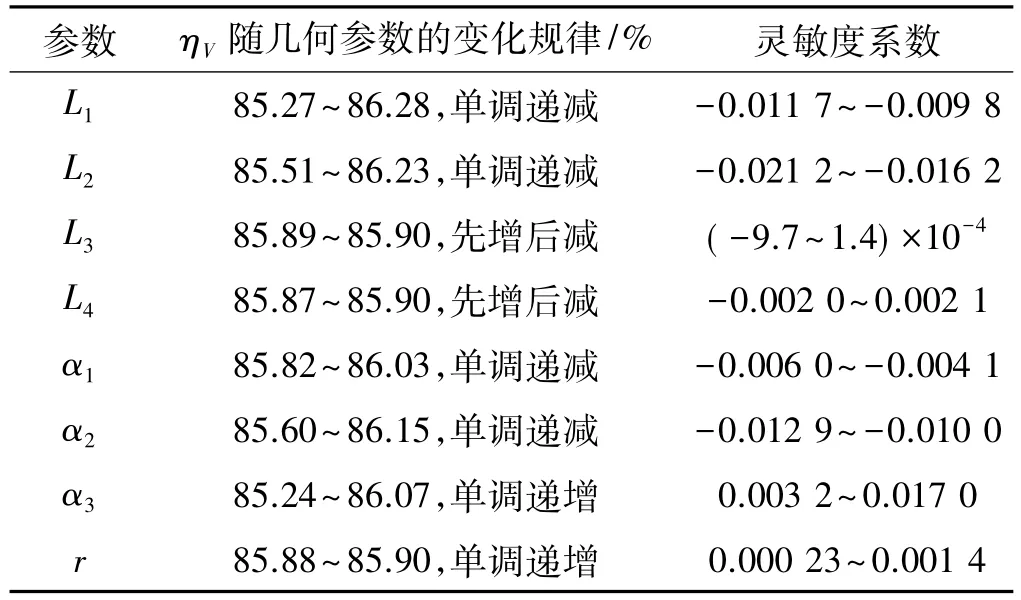
表5 ηV对几何参数的灵敏度系数计算结果Table 5 Results of the geometric parameters sensitivity coefficient for ηV

结果表明，翼柱形发动机的体积装填分数对各几何参数的灵敏度系数整体偏小，但是各参数的灵敏度数值间差距较大。ηV随 L1、L2、α1和 α2的增大呈单调递减趋势;随L3和L4的增大呈现先增加后减小的趋势，存在装填分数的极大值;随α3和r的增大呈单调递增趋势。几何参数灵敏度系数按由高到低的顺序排列为:L2，α3，α2，L1，α1，L4，r，L3。

综合以上2组分析结果可以得知，在8个相关参数中，L3的灵敏度系数最低。而且与其在灵敏度排序中相邻的参数r相比，L3的灵敏度要小很多。因此，可以认为L3是钝感参数，在接下来的优化设计中直接将其设置为默认值，并不参与优化计算。

3 考虑结构完整性和体积装填分数的发动机药形优化

固体发动机药形优化设计从总体上可以分为3步:建立优化模型，把工程结构的设计问题变成一个数学问题;选择一个合理、有效的优化方法;编制优化程

序进行求解，得到最优参数。

3.1 优化模型与方法

本文对所研究的翼柱型发动机进行药形优化时，主要考虑了2个技术指标:药柱结构完整性和药柱体积装填分数。考虑到发动机结构已基本定型，故而选择药柱的结构响应最小为优化目标，而以体积装填分数为约束条件。该优化模型可以描述为

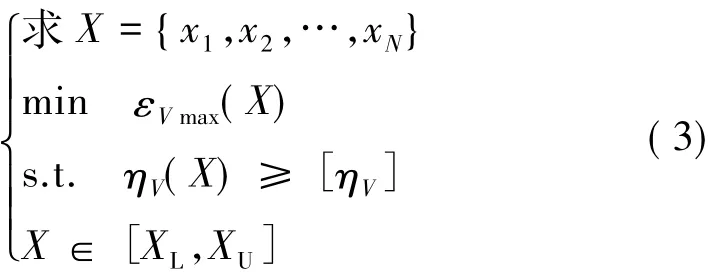
式中 X为设计变量，即药柱的几何参数;N为变量数目;ηV(X)为药柱的体积装填分数;εVmax(X)为药柱的最大Von Mises应变;［ηV］为体积装填分数限定值;XL和XU分别为设计变量的下限和上限。

根据几何参数的灵敏度分析结果，排除钝感参数L3后，将剩余的 7个参数作为设计变量，即 X={L1，L2，L4，α1，α2，α3，r}。在进行优化设计时，所设定的几何参数取值范围较大，在优化过程中可能因为参数不协调而出现不可行解，所以要根据药柱的几何结构对几何参数的取值进行检验，无法通过检验的参数取值不进行建模计算。

由于药柱体积装填分数和结构响应的函数表达式很难获取，因此对连续性和可微性有较高要求的传统优化方法不再适用。综合考虑计算的精度和效率，本文采用遗传算法对翼柱形发动机进行优化。

3.2 遗传算法设计

在进行药形优化时，将设计变量的数据类型限定为整数取值，并采用整数编码的方式。适应度函数表征个体适应环境的能力，与目标函数和约束条件相关，将其定义为

基本遗传算子包括选择算子、交叉算子和变异算子，分别用于模仿生物遗传与进化的各种自然现象。为了保证遗传操作的有效性，必须对各算子进行设计，经过设计的遗传算法流程图如图7所示。

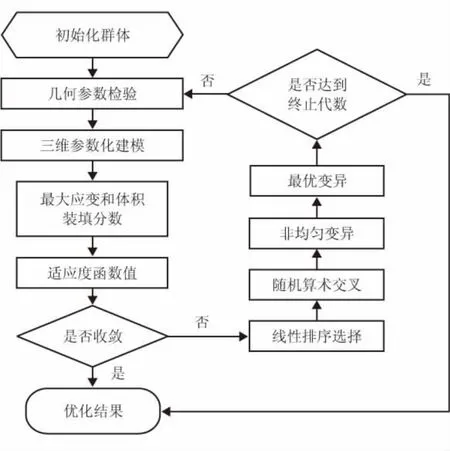
图7 遗传算法流程图Fig.7 Flow chart of genetic algorithm

3.3 优化结果

按照设定的控制参数执行遗传算法，算法运行33代后收敛，优化历程如图8所示。

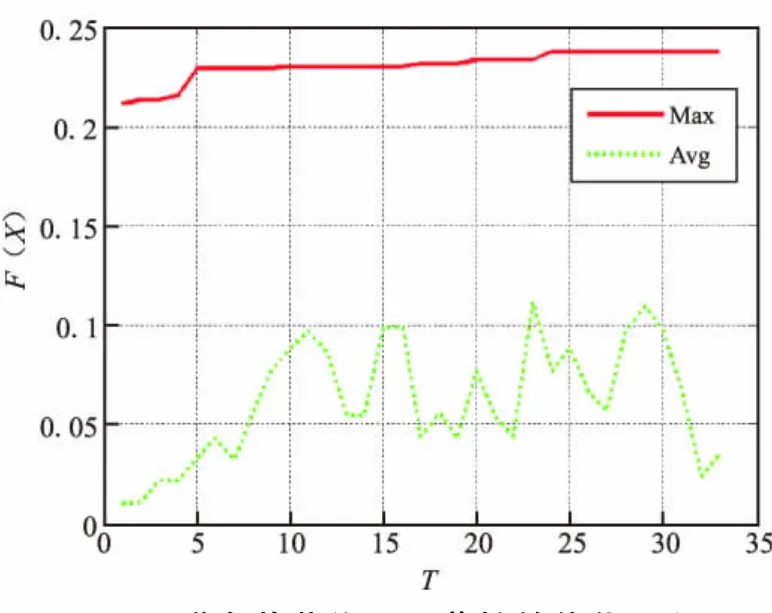
图8 联合载荷作用下药柱的优化历程Fig.8 Optimization process of the grain under combined load

图8中，F(X)为适应度函数值，T为遗传代数，Max和Avg分别为群体适应度最大值、平均值的曲线。从图8可看出，随着优化过程向前推进，适应度F(X)的最大值呈递增态势，这表明，优化结果越来越趋向于最优值。

设计变量X的初始参数为X={193，410，534，65，38，50，85}，在初始参数下药柱的Von Mises应变云纹图见图9。经遗传算法优化后，最优设计变量为X={131，408，464，64，40，72，89}，在该参数下药柱的 Von Mises应变云纹图见图10。

在联合载荷作用下，优化前药柱的最大Von Mises应变值为29.8%，体积装填分数为85.9%;优化设计后，形状最优药柱的最大Von Mises应变值为26.4%，体积装填分数为86.37%，优化前后药柱的最大应变值均出现在大翼槽与圆管段连接处的侧壁上。对比后可知，最优药形的εVmax(X)比原始药形降低了11.41%，而ηV相对增加了0.55%。

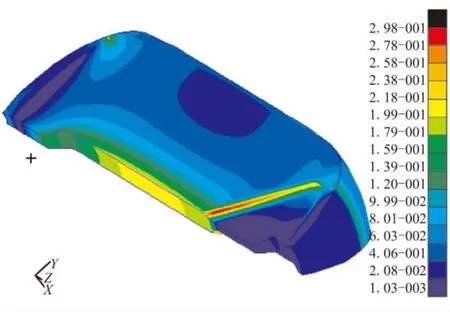
图9 优化前药柱的Von Mises应变云纹图Fig.9 Von Mises strain distribution of the grain before optimization

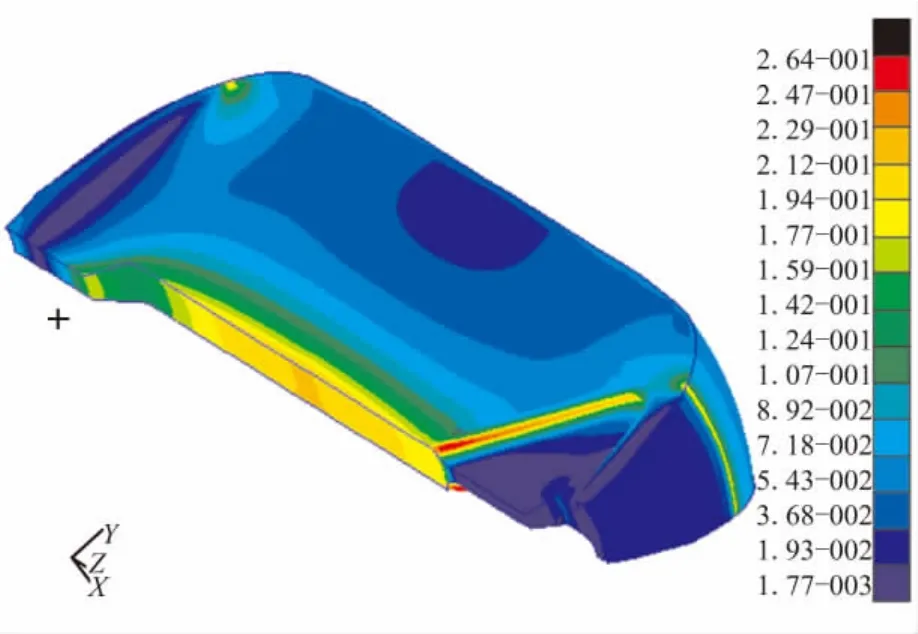
图10 优化后药柱的Von Mises应变云纹图Fig.10 Von Mises strain distribution of the grain after optimization

此外，在优化前后，影响发动机燃烧室压强的药柱参数如喷喉面积、燃速系数、药柱密度、压强指数等基本保持不变，而装填分数的增加直接导致初始燃面发生了微小的变化(由0.411 m2降低到了0.381 m2)。由于燃面的变化量不大，处于可控范围，因此对发动机内弹道性能的影响有限，内弹道曲线的平稳性可得到保证。

4 结论

提出了基于三维参数化建模和遗传算法的固体发动机药形优化设计方法，并利用该方法对某实际型号翼柱形发动机进行了药形优化。优化结果显示，最优药形的εVmax比原始药形降低了11.41%，而ηV相对增加了0.55%，且优化后的药形能基本保证发动机的内弹道性能，达到了优化效果。所提方法可用于多种固体火箭发动机的药形优化设计，具有一定的工程实用价值。

［1］陈汝训.固体火箭发动机设计与研究［M］.北京宇航出版社，1991.

［2］Raza M A，Liang W.Design and optimization of 3D wagon wheel grain for dual thrust solid rocket motors ［J］.Propellants，Explosives，Pyrotechnics，2013，38:67-74.

［3］Kamran Ali，Liang Guo zhu.Design and optimization of 3D radial slot grain configuration ［J］.Chinese Journal of Aeronautics，2010，23:409-414.

［4］杨涓，戎海武，朱燕堂，等.固体发动机药柱优化设计［J］.推进技术，1997，18(2):98-102.

［5］窦毅芳，王中伟，张为华，等.稳健优化设计及其在固体火箭发动机装药设计中的应用［J］.固体火箭技术，2007，30(6):478-481.

［6］王锟，刘旸，蔡体敏.基于数据库技术的固体火箭发动机结构优化设计方法［J］.固体火箭技术，2010，33(2):171-175.

［7］李磊，申志彬，唐国金，等.考虑结构完整性和装填分数的星形药柱形状优化 ［J］.推进技术，2011，32(2):235-239.

［8］李磊，段静波，申志彬，等.基于参数化建模的药柱伞盘结构形状优化 ［J］.固体火箭技术，2011，34(5):584-589.

［9］王元有.固体火箭发动机设计［M］.国防工业出版社，1984.

［10］申志彬，唐国金，雷勇军.基于Patran二次开发的星形药柱结构分析与设计［J］.固体火箭技术2009，32(2):175-179.

(编辑:薛永利)

Optimization of finocyl grain based on the three-dimensional parameterized modeling

ZHANG Wei-xing，TANG Guo-jin
(College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Increasing loading fraction is one of the most significant way to promote the total impulse of solid rocket motor(SRM)，however，it will give rise to a higher grain stress and strain at the same time，which is obviously harmful to the structural integrity of SRM.In order to solve this problem，one kind of optimization method of SRM based on the three-dimensional parameterized modeling and Genetic Algorithm(GA)was proposed.Firstly，the parameterized model of one finocyl grain were achieved with PCL(Patran Command Language)of MSC.Patran.Then parameter sensitivity analysis of the grain under thermal and pressure loading was conducted.On the basis of all the work mentioned upon，configuration optimization of the grain was realized with the method of GA.On condition that the loading fraction does not decrease，the best grain shape with the minimum Von Mises strain was found.The method proposed in the paper could be used for grain shape optimization of kinds of SRM，which has definite engineering practical value for the improvement of structural integrity of the SRM grain with high loading fraction.

grain shape optimization;structural integrity;loading fraction;three-dimensional parameterized modeling;sensitivity analysis;GA

V435+.21

A

1006-2793(2014)04-0490-06

10.7673/j.issn.1006-2793.2014.04.011

2013-09-09;

2013-10-16。

国家自然科学基金(11272348)，国防科技大学科研计划资助项目(JC13-01-03)。

张维星(1990—)，男，硕士，研究方向为导弹和火箭结构完整性。E-mail:zhongnanzwx@163.com