考虑土应力历史的土压力计测量修正*

王继成，龚晓南，田效军

(1. 浙江大学 滨海和城市岩土工程研究中心，浙江 杭州 310058；2. 台州职业技术学院 建工学院，浙江 台州 318000；3．浙江省电力设计院，浙江 杭州 310012)

土压力计与周围土的力学性质差异较大，改变了土中原来的应力场，土压力计测得的土压力偏离实际土压，曾经有很多学者对土压力计测量值修正方法进行了研究[1-2]，近年来Ahangari(2010)研究了土压力计与周围介质的刚度比值对土压力计测量的影响[3]，WACHMAN G S(2011)研究了土压力计表面应力分布与测量值的关系[4]，Talesnick(2013)研究了土的类别、颗粒尺寸、强度、应力历时等与土压力计测量值之间的关系，并探索了试图减少这些因素影响的方法[5].我国学者韦四江等(2009)研究了微型土压力计的载荷系数K值与工作介质之间的关系，并对微型土压力计进行了标定[6].曾辉等(2001)提出了两次压陷理论，并推导出匹配误差理论计算公式[7].

目前温度对土压力计的影响研究比较多，温度修正方法比较成熟[8-9].各种新型结构、特殊用途或功能的土压力计研究和设计也较多[10]，对土压力理论及其计算研究的也很多，如王俊杰(2004)对刚性挡土墙被动土压力进行了研究[11]，陈昌富对滑裂面非极限状态土压力进行了分析[12]，都取得了可喜的成果，但对考虑土应力历史的土压力计修正研究的较少.

1 欠固结土(未压实土)

回填土中埋入土压力计后，回填土没有压实，由于土的压缩模量一般小于土压力计的等效弹性模量(即带空腔的土压力计的等效模量，它的受压面为感应膜)，土压力计的应变小于土的应变，所以土压力计比同样大小的土分担的压力大，使土压力计测得的土压力大于实际土压力.土的压缩模量就是土体在完全侧限条件下，竖向附加应力σZ与相应的应变增量εZ之比，即

(1)

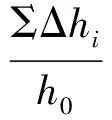
实验结果表明[10]，随着荷载的增大，同样大小的荷载增量引起试样的压缩量Δhi+1逐渐变小，从式(1)可以看出，对于未压实土，压缩模量ESi随土压力增大逐渐增大，土压力计分担的压力逐渐增大，土压力计测量值逐渐接近实际土压力.

1.1 欠固结土土压力测量值修正

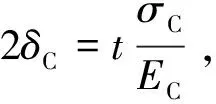
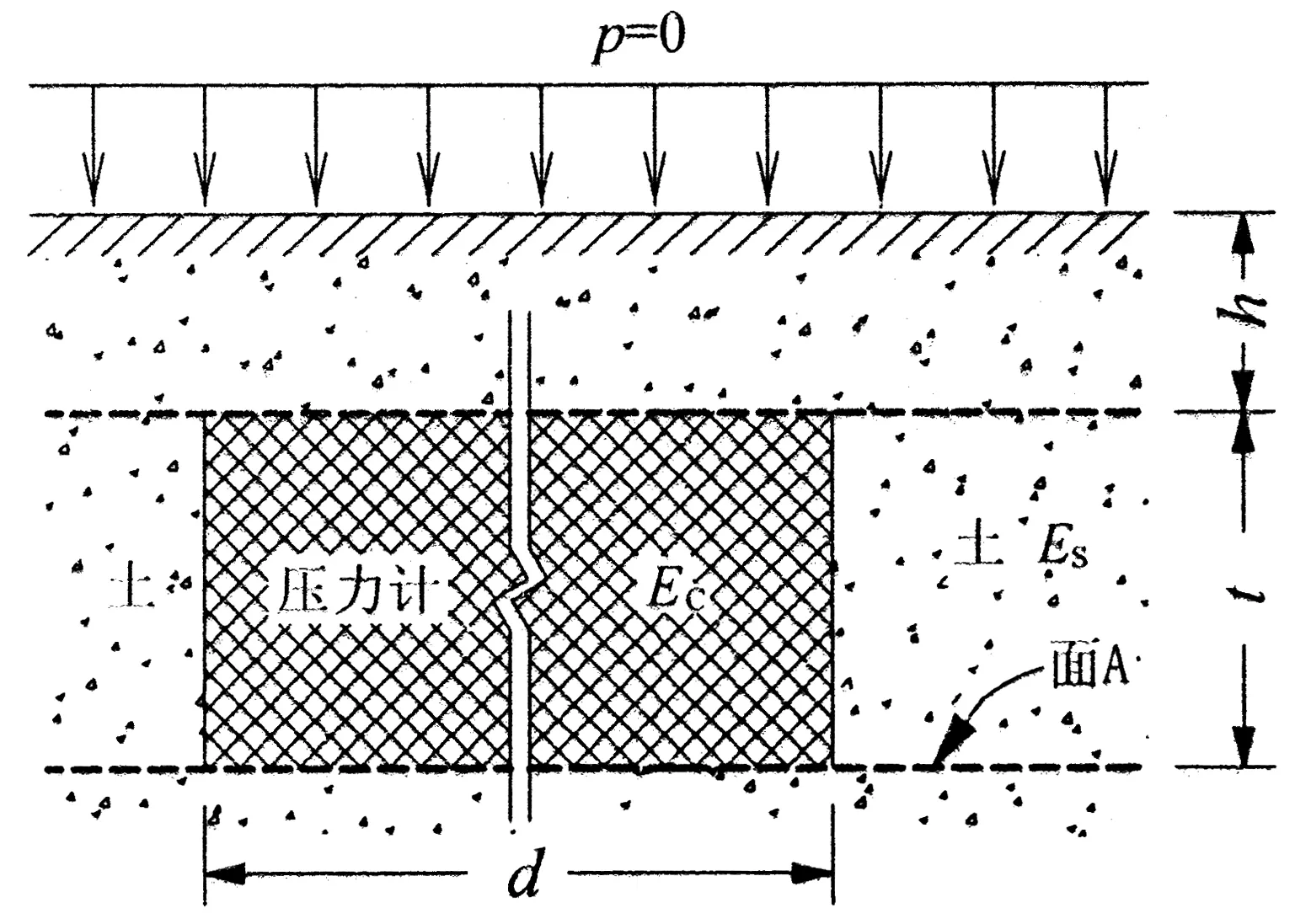
图1 虚土铺填

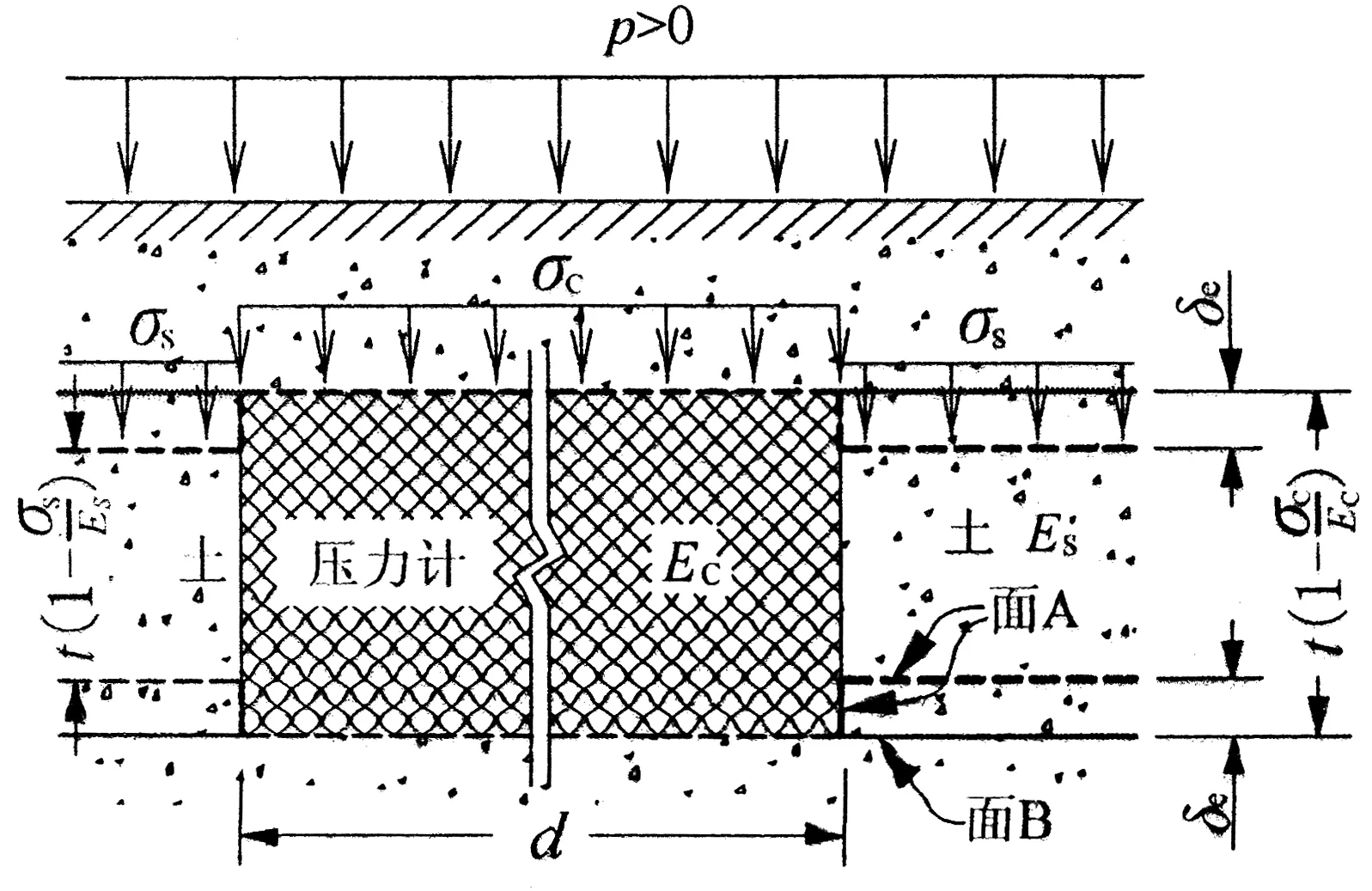
图2 首次加载

一般地EC>ES，则土比压力计多压缩2δe，即图1中的上下两个平面A各产生一个凹陷，如图2中的粗虚线所示，凹陷深度为：

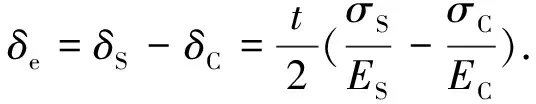
(2)

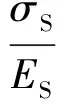
直径为d的刚性圆盘，在荷载πd2(σC-σS)/4的作用下，TIMOSHENKO G等给出了刚性圆盘在半无限弹性体的表面上产生的凹陷深度计算表达式[13]：

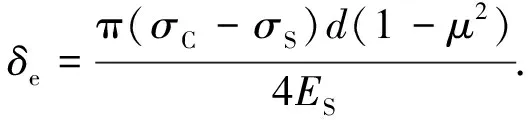
(3)

式中：μ为土的泊松比；ES为土的压缩模量.

由式(2)和式(3)得：

(4)

式中ξ为两式计算误差.

由式(4)变换可得匹配系数α：

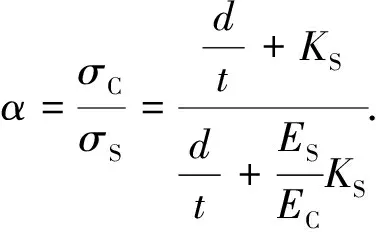
(5)

或

(6)

式中

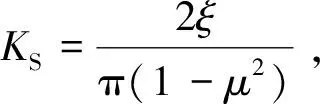
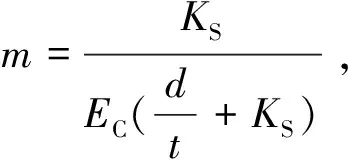
由式(5)可以看出，土压力计厚度t越小，直径d越大，匹配系数α越接近于1，土压力计测量值σC越接近实际土压力σS，测量越精确.一般地，土压力计的模量大于土的模量，从式(5)还可看出，当土的模量接近土压力计的模量，土压力计测得的土压力就接近实际土压力.疏松的回填土中的土压力计测量匹配系数大于1，当土被压实后，土的模量增加，匹配系数就接近于1.

1.2 欠固结土土压力测量实验

土压力计采用某厂生产的振弦式土压力计，厚度t=25 mm，直径d=108 mm.土样采用某河砂，含水量1.4%，各粒径的土粒含量如表1所示，取部分试样在固结仪里做压缩实验，测出该试样在各级压力作用下的压缩模量.实验箱如图3所示，尺寸为60 cm(长)×40 cm(宽)×60 cm(高)，四壁光滑，并涂抹滑石粉，再贴塑料薄膜，以减少土与实验箱壁的摩擦力.Theroux等用一个圆柱形钢桶做了土压力计标定实验[4，14]，他们在土压力计的上下方各设一只装满油的橡胶囊，橡胶囊与油压表相连，测试时发现土压力计的上下方的橡胶囊的油压几乎相同，说明砂子与钢桶壁的摩擦非常小，可以忽略不计.所以本实验的砂土与模型槽的四壁之间的摩擦力可忽略不计.将砂土铺到实验箱内，土压力计平放在实验箱的中部，采用万能材料试验机加压，测得各级荷载作用下的土压力计测量值，算出匹配系数，如图4所示.

表1 粒组含量

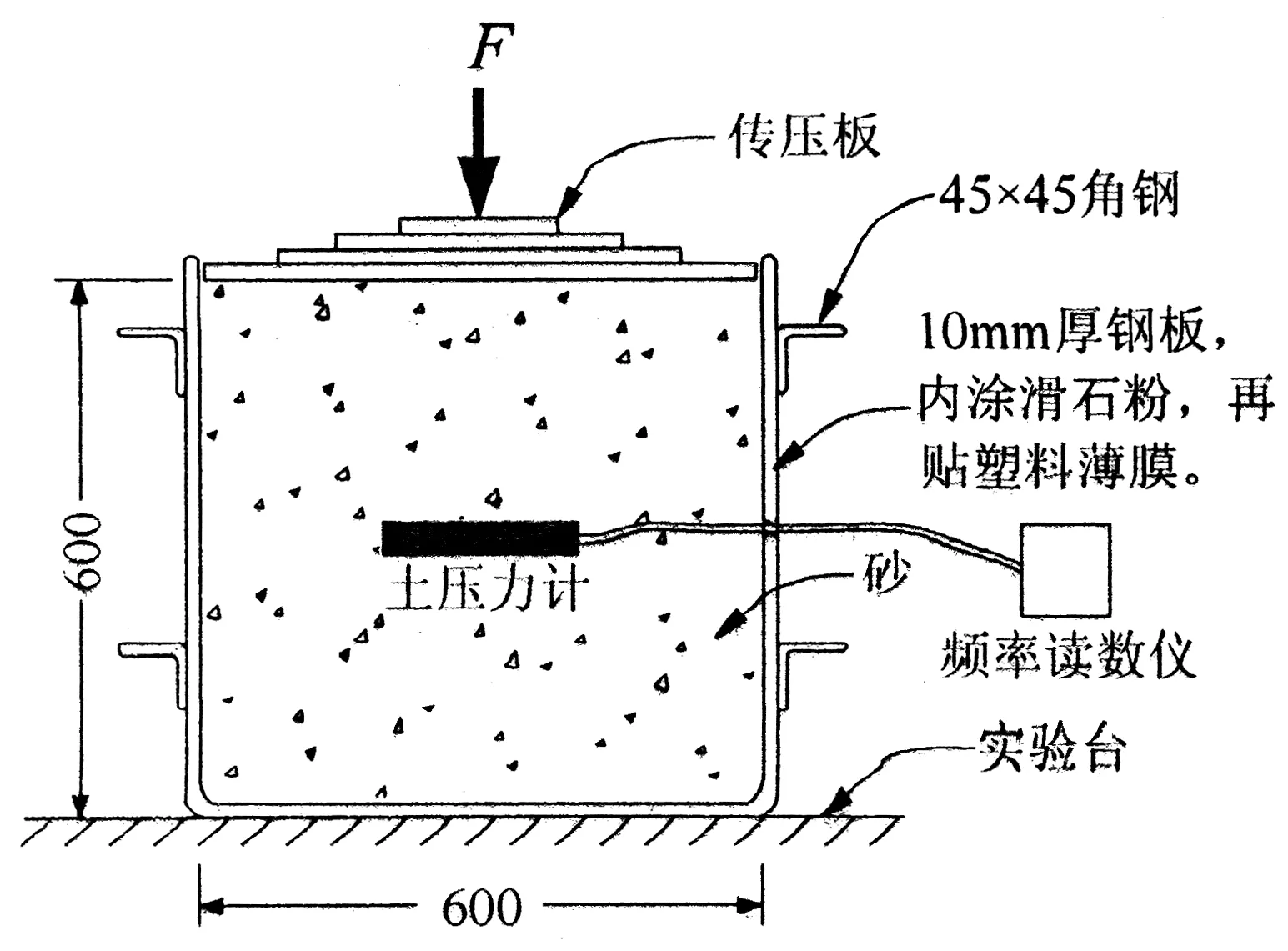
图3 实验箱剖面图(mm)

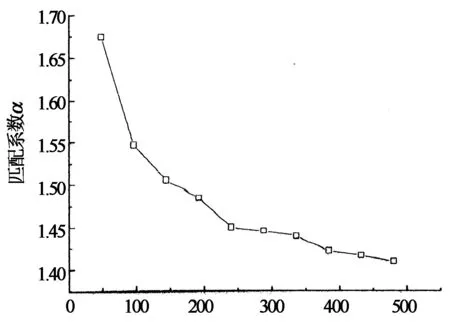
压力/kPa

从图4可以看出，对于虚铺的松砂，始终有匹配系数α大于1，即σC>σS，但随着荷载的增大而逐渐减小，减小的幅度也逐渐减小，土压力计测量值越来越接近实际土压力.Theroux等[4, 14]、西南交通大学的张胜利[10]的标定实验也得到类似的数据.将压缩模量ES及与之对应的1/α绘制于图5中，可以发现1/α与ES近似呈线性关系，所以m，n和KS为常数.

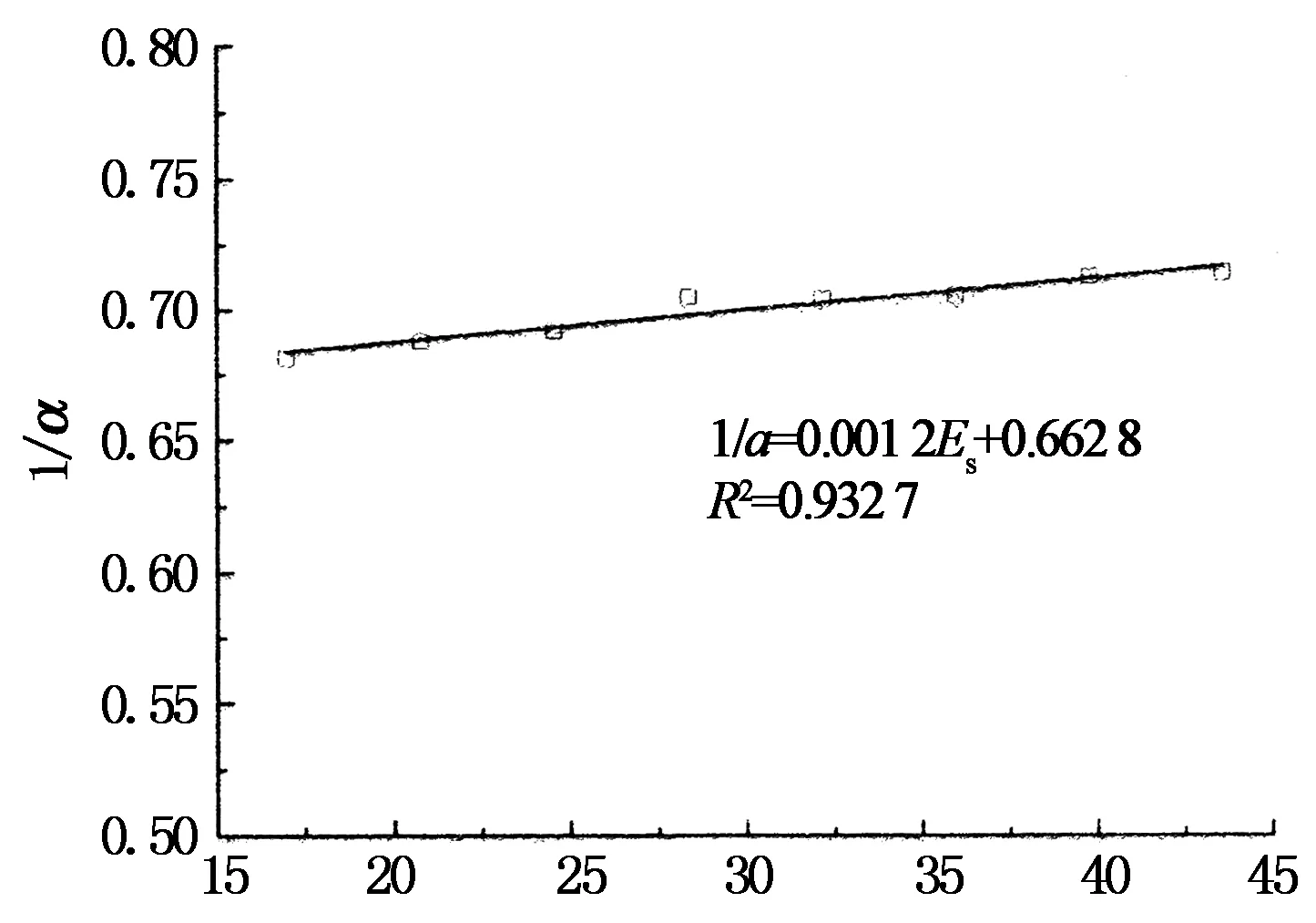
ES/MPa

由图5拟合得到

(7)

则：

σS=σC/α=σC(0.001 2ES+0.662 8)．

为了得到足够视野亮度，必须用强光源并开大光栅，使充足的光源进入物镜。同样条件下，物镜头放大倍数越大，镜口率越高，进入光线越少。因此，转换物镜头时应注意调整光线强度，使用油镜头时一定要添加香柏油。聚光镜抬高接近物镜头可以增加亮度，如果亮度已经足够甚至过剩，可以缩小光圈，或者下调聚光镜，但一般不降低底座光源强度，因为会使光源的颜色由白变黄，失去自然光属性，改变物像的颜色。下调聚光镜不仅可以降低亮度，还可以增加物像的对比度，使物像层次清晰。

(8)

式中：ES为欠固结土的压缩模量，可通过现场或室内实验得到，MPa；σS和σC分别为实际土压力和土压力计测量值，kPa.根据图5和式(6)可得：

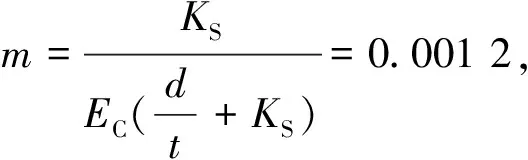
(9)

(10)

解得EC=281 MPa，KS=2.2.

用某公司生产的微型土压力计(直径d=20 mm，厚度t=8 mm)做了同样的实验，1/α与ES之间的线性关系也很好，拟合后得m=0.003 1，n=0.542 3，解得KS=2.19，土压力计等效模量为147.6 MPa，说明式(6)也同样适用于微型土压力计.与普通土压力计相比，微型土压力计的厚径比大，测得的匹配系数比普通土压力计的匹配系数大11.2%左右，说明微型土压力计的测量误差较大.另外微型土压力计的匹配系数分布范围也较大，1.458～1.940，而普通土压力计为1.41～1.67，说明微型土压力计的匹配系数对欠固结土的压缩模量的变化比较敏感，所以建议在使用微型土压力计时须考虑土压缩模量的变化，否则误差会较大.

采用同样的土，不同的土压力计，测得的KS都是相同的；或者采用同一土压力计，不同的土样，测得的土压力计的等效模量EC也是相同的，所以在土压力测试前可通过实验得到KS和EC，即可通过式(6)计算匹配系数，从而修正土压力计测量值.式(6)中欠固结土的压缩模量ES是随着压力的增大而增大的，难以直接确定，可用迭代法来确定.先凭经验估计ES，和土压力计测量值σC一起代入式(6)，试算得到一个σS，再根据欠固结土的ES-σS关系得到一个相对较准确的ES，并和σC一起代入式(6)可得到一个较准确的σS，依此类推，经过反复迭代后可得到比较精确的ES，再由式(6)来修正土压力计测量值.砂性回填土的压缩模量变化范围一般在25～45 MPa左右，从图5可以看出， 1/α变动范围较小，所以在土压力测量精度要求不高时，可以根据经验直接设定一个恒定的ES代入式(6)进行修正，从而简化计算.

2 超固结土

在回填土中埋入土压力计后，将回填土压实，压实荷载卸载后土体回弹，再次受压时(继续填土或施加工作荷载)，如果压力没有超过先期压实荷载(先期固结压力)，则该回填土为超固结土，再受压时的压力主要消除回弹，产生的压缩变形近似为弹性变形；当再受压时的压力超过先期固结压力时，土又转变为欠固结土，土体产生的变形以塑性变形为主.

2.1 超固结土的土压力测量值修正

由于土的模量比土压力计的模量小，卸载后，土压力计四周土的回弹大于土压力计的回弹，土压力计的感应板脱离原先与之接触的土而形成缝隙，如图6所示.再加载时，由于缝隙的存在，开始时土压力计感应板受力很小，如图7、图8所示，压力计测量值明显小于周围的土的实际土压力，匹配系数小于1.Theroux等用压实的密实砂土做标定实验也出现类似现象[4, 14]，张胜利用粗砂、细砂、不同水泥含量的水泥稳定土分别做了加载、卸载时的土压力计标定实验，他的卸载实验也出现了土压力计测得的土压力小于实际土压力的现象[10].随着荷载的增大，缝隙逐渐变小，土压力计测量值逐渐增大并接近实际土压力.继续加载，土压力计测量值超过实际土压力，匹配系数大于1，如图8所示.

图6 卸载示意图

图7 再加载示意图

土压力/kPa

随着加载、卸载次数的增加，土的压缩模量增大并逐渐稳定，卸载后的土压力计感应板与土之间的缝隙逐渐变小，匹配系数越来越大，其与土压力之间的关系逐渐趋于稳定，如图8所示，对于干河砂，加载到第4次时匹配系数与土压力之间的关系就基本稳定了.从图8可以看出，除了土压力接近最大固结压力时以外，重复加载时的匹配系数与土压力具有很好的线性关系，这与首次加载不同.本实验共加载、卸载10次，剔除第10次加载的线性关系较差的后面几个点，对第10次加载时的匹配系数与土压力进行拟合，结果如式(11)：

(11)

即

(12)

式中：σS和σC单位为kPa.

将土压力计测量值σC代入式(12)算出实际土压力σS.对于超固结土，当再加载时的土压力小于先期固结压力时，匹配系数随压力的增大而增大，土压力测量值可按照本节方法修正.当再加载时的土压力大于先期固结压力时，土又重新成为欠固结土，和前面的欠固结土一样，匹配系数又随土压力的增大而减小，可按照前面的欠固结土的方法来修正土压力计测量值.

2.2 先期固结压力的确定

通过压缩实验可以确定各级固结压力σS作用下的土的压缩模量ES，建立ES-σS关系曲线.根据现场土压力计周围的超固结土的压缩模量ES，对照ES-σS关系曲线，即可得到先期固结压力σSp.根据式(12)得到与先期固结压力σSp对应的土压力计测量值σCp.当土压力计测量值σC小于σCp时，表示土为超固结土，否则为欠固结土.

3 算 例

赣(州)龙(岩)铁路GDRl44+100～GDRl44+165段返包式土工格栅加筋土挡土墙断面图如图9所示，墙高12.2 m，格栅竖向间距0.5 m.墙体上部7.5 m厚采用粘性土回填，墙下部采用碎石土回填，机械振动碾压密实.土压力计采用某厂生产的振弦式土压力计，厚度t=25 mm，直径d=108 mm，压力计布置如图9所示，其中底层土压力计测得的竖向土压力如图10所示(已考虑温度因素).

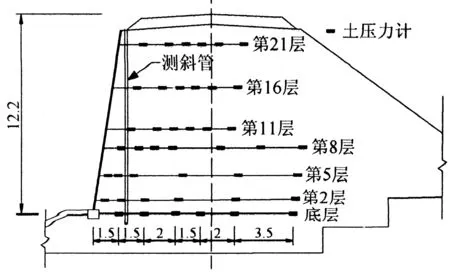
图9 土压力计布置图(m)

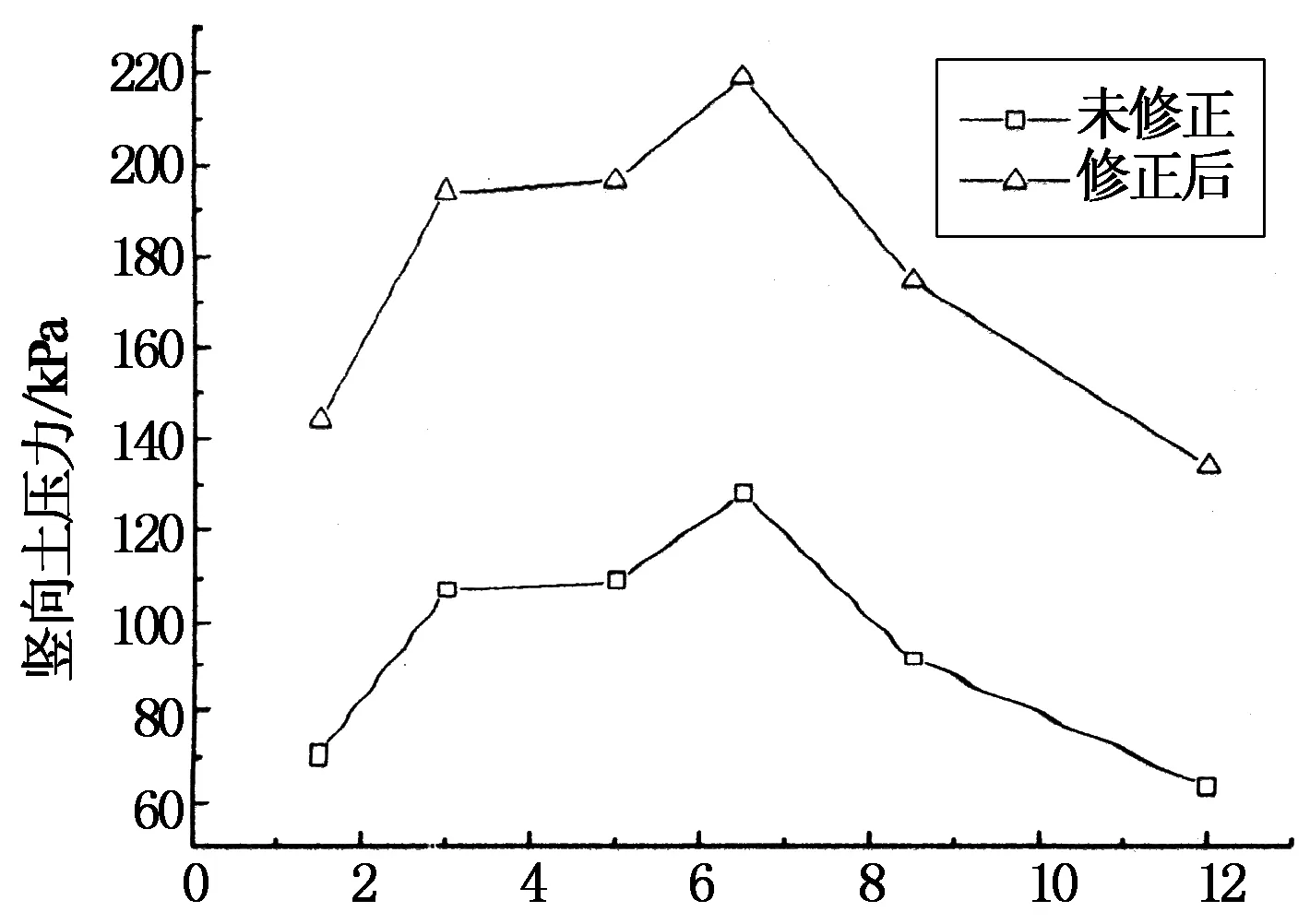
距墙面距离/m

填土重度18 kN/m3，填土高10 m，那么最大竖向土压力应该超过180 kPa，而图10中最大竖向土压力只有128 kPa，土压力计测得的未修正的竖向土压力明显小于理论计算值，所以必须对土压力计测量值进行修正.由于现场采用机械振动碾压，所以很难确定碎石回填土的先期固结压力，但可以根据现场检测的回填土压缩模量反算先期固结压力.取类似于底层格栅处的松散回填土样(剔除大粒径石子)进行压缩实验，建立各级固结压力σS与压缩模量ES之间的关系.根据现场碾压施工检测结果，振动碾压后土的压缩模量为40 MPa，通过ES-σS关系可知与40 MPa对应的先期固结压力σSp=850 kPa.按照第2.2节所述的方法，将松散的碎石土铺到实验箱内，并在碎石土的中部水平放置土压力计，逐级加载至850 kPa，记录各级荷载下的匹配系数，根据固结压力与压缩模量之间的关系，建立匹配系数与压缩模量之间的关系，拟合得到

(13)

对于欠固结土的土压力计测量值可按照式(14)修正：

σS=σC/α=σC(0.000 9ES+0.675 3)

(14)

再反复卸载、加载直到匹配系数与压力关系稳定后，绘制固结压力σS与匹配系数α的关系曲线，剔除土压力接近先期固结压力时的几个线性关系不好的点，对剩余的点进行线性拟合，得：

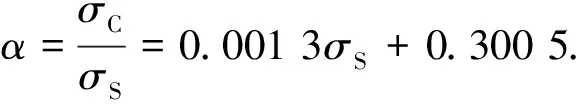
(15)

即：

(16)

当回填土高10 m时底层土压力计测得的最大土压力处距墙面6.5 m，σC=128 kPa，代入式(16)可得σS=219 kPa，小于先期固结压力σSp(850 kPa)，为超固结土，用式(16)修正土压力.这里如果算得的σS>σSp，说明土又成为欠固结土，则应该根据式(14)修正土压力.本工程的填土最厚为12.2 m，显然土自重产生的竖向土压力都没有超过先期固结压力，所以各点的土压力都可采用式(16)修正，修正后的土压力如图10所示.

图10中填土高10 m时修正后的竖向土压力曲线与水平轴(即σS=0轴)所夹的区域面积为2 105 kPa·m，即每米长的挡土墙重量是2 105 kN，底层格栅长12 m，则平均竖向压力为2 105 kPa·m /12 m=175.4 kPa，可算出回填土的平均重度为175.4 kPa/10 m=17.54 kN/m3，这与实测结果较接近，说明土压力修正正确.

4 结论与探讨

通过上面分析可以得到如下结论：

1)土压力计测量值与实际土压力存在较大差异，该差异随着土的压缩模量、土的应力历史的变化而变化.

2)对于欠固结土，土压力计测量值往往大于实际土压力，随着压力的增大，土的压缩模量逐渐增大，匹配系数逐渐减小，但匹配系数始终大于1，土压力可按照本文第1节方法修正．

3)对于超固结土，在土压力较小时，土压力计测量值小于实际土压力，当土压力较大时，土压力计测量值大于实际土压力.对于超固结土，土压力可按本文第2节方法修正.

笔者曾经做过不同河砂样本的压缩实验，有的河砂为洁净河砂，有的河砂掺入了较多的粘粒成分，实验都得到了相同的结论.对于饱和的土样，或者压缩后可能变饱和的土样，如果粘粒含量较多，有可能会产生较大的孔隙水压力，土压力测量变得很复杂，本文结论不适用.

关于进一步研究的探讨：将本文的研究内容推广开来，当土压力计测水平方向土压力时，土的水平方向的应变对土压力计的测量结果可能会产生较大影响，这有待于进一步研究.

[1] PEATTIE K R, SPARROW R. The fundamental action of earth pressure cells [J]. Journal of the Mechanics and Physics of Solids, 1954, 2(3): 141-155.

[2] TORY A, SPARROW R. The influence of diaphragm flexibility on the performance of an earth pressure cell [J]. Journal of Scientific Instruments, 1967, 44(9): 781.

[3] AHANGARI K, NOORZAD A. Use of casing and its effect on pressure cells [J]. Mining Science and Technology, 2010, 20(3): 384-390.

[4] WACHMAN G S, LABUZ J F. Soil-structure interaction of an earth pressure cell [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(9): 843-845.

[5] TALESNICK M. Measuring soil pressure within a soil mass [J]. Canadian Geotechnical Journal, 2013, 50(7): 716-722.

[6] 韦四江, 王大顺, 郜进海, 等. 微型土压力盒的标定及修正 [J]. 地下空间与工程学报, 2009, 5(5): 1003-1006.

WEI Si-jiang, WANG Da-shun, GAO Jin-hai,etal. Calibration and correction of miniature earth pressure cell [J]. Chinese Journal of Underground Space and Engineering, 2009, 5(5): 1003-1006. (In Chinese)

[7] 曾辉, 余尚江. 岩土压力传感器匹配误差的计算 [J]. 岩土力学, 2001, 22(1): 99-105.

ZENG Hui, YU Shang-jiang. The calculation of matching error of rock-soil pressure transducer[J]. Rock and Soil Mechanics, 2001, 22(1): 99-105. (In Chinese)

[8] DAIGLE L, ZHAO J Q. The influence of temperature on earth pressure cell readings [J]. Canadian Geotechnical Journal, 2004, 41(3): 551-559.

[9] GB/T 13606—2007.土工试验仪器 岩土工程 器振弦式传感器 通用技术条件[S]. 北京：中国标准出版社，2007.

GB/T 13606—2007. Instrument for geotechnical engineering—General specifications of vibrating wire sensor[S].Beijing:Standards Press of China,2007． (In Chinese)

[10]张胜利. 土压力传感器与土介质相互作用特性分析 [D]．成都：西南交通大学土木工程学院, 2010.

ZHANG Sheng-li. Properties analysis on interaction of soil pressure sensor and soil medium [D]. Chengdu:School fo Civil Enginering，Southwest Jiaotong University， 2007. (In Chinese)

[11]王俊杰, 朱俊高, 魏松. 刚性挡土墙被动土压力的计算及影响分析 [J]. 哈尔滨工业大学学报, 2004, 36(11): 1483-1486.

WANG Jun-jie, ZHU Jun-gao, WEI Song. A generalized computing equation and influencing factors of passive earth pressure acting on rigid retaining wall[J]. Journal of Harbin Ins Titute of Technology, 2004, 36(11): 1483-1486. (In Chinese)

[12]陈昌富, 肖重阳, 唐仁华. 基于 PSO 搜索潜在滑裂面非极限状态土压力计算 [J]. 湖南大学学报:自然科学版, 2013, 40(2): 9-14.

CHEN Chang-fu, XIAO Chong-yang, TANG Ren-hua. Computation of earth pressure under non-limit state based on PSO search of Potential slip surface[J]. Journal of Hunan University:Natural Sciences, 2013, 40(2): 9-14. (In Chinese)

[13]TIMOSHENKO G. Theory of elasticity [M]. 3 ed. NewYork: McGraw Hill Book Company, 1970.

[14]LABUZ J F, THEROUX B. Laboratory calibration of earth pressure cells [J]. ASTM Geotechnical Testing Journal, 2005, 28(2):51,59,60,188-196.