柱端弯矩增大系数对PC框架结构抗震性能影响的研究*
2014-09-18张耀庭卢怡思杜晓菊卢杰志
张耀庭,卢怡思,杜晓菊,卢杰志
(1.华中科技大学 土木工程与力学学院,湖北 武汉 430074;2.中信建筑设计研究总院有限公司, 湖北 武汉 430014)
我国规范[1-3]针对不同抗震等级的框架结构,通过设置柱端弯矩增大系数(见表1)来达到延性框架设计时的 “强柱弱梁”要求.近年来,国内外学者针对普通钢筋混凝土框架结构柱端弯矩增大系数的合理取值问题研究[4-8]很多,但有关预应力混凝土框架结构的研究则相对较少.《预应力混凝土结构抗震设计规程》(JGJ 140-2004)(以下:简称04规程)是在《建筑抗震设计规范》(GB 50011-2001) (以下:简称01规范)的基础上编制的,自2010年以来,《建筑抗震设计规范》(GB 50011-2010)(以下:简称10规范)在我国开始全面实施,10规范中钢筋混凝土框架结构的柱端弯矩增大系数较01规范已有很大的提高,这样,在预应力框架结构的抗震设计中,就存在着新旧规范难以匹配,包括柱端弯矩增大系数在内的延性框架设计系数难以取值等现实问题.为此,本文将按我国现行04规程设计多层多跨预应力混凝土框架结构,对其进行静力弹塑性和动力弹塑性时程分析,探讨柱端弯矩增大系数对预应力混凝土框架抗震性能与耗能机制的影响,以期对该系数的合理取值提供参考.

表1 各规范关于柱端弯矩增大系数的规定
1 预应力混凝土框架结构的设计
本文以04规程为依据,以某预应力工程为样本,共设计了6个两跨三层的预应力混凝土框架结构,抗震设防烈度为8度(0.2 g)、设计地震分组为第一组、场地类别为二类.柱网尺寸为6 m×15 m,预应力梁跨度为15 m,房屋总高度15.6 m,其中,底层高6 m,其余层高均为4.8 m,框架的抗震等级为二级,设计使用年限为50年,场地特征周期值为0.35 s.设计计算时,结构的阻尼比取0.03,考虑填充墙对结构的刚度作用,结构的周期折减系数为0.8.屋面板与楼板的厚度均为120 mm,环境类别为一类.各构件的混凝土强度等级及所用钢筋类型如表2所示.预应力筋采用1860级φS15.2高强低松弛钢绞线,裂缝控制等级为2级.采用水磨石楼面与地砖保护层屋面,屋面布置900 mm高女儿墙,框架填充墙及女儿墙等围护结构均采用250 mm厚A3.5蒸压加气混凝土砌块.由于结构总高仅15.6 m,在设计中不考虑风荷载的作用.结构上的恒、活载信息见表3.
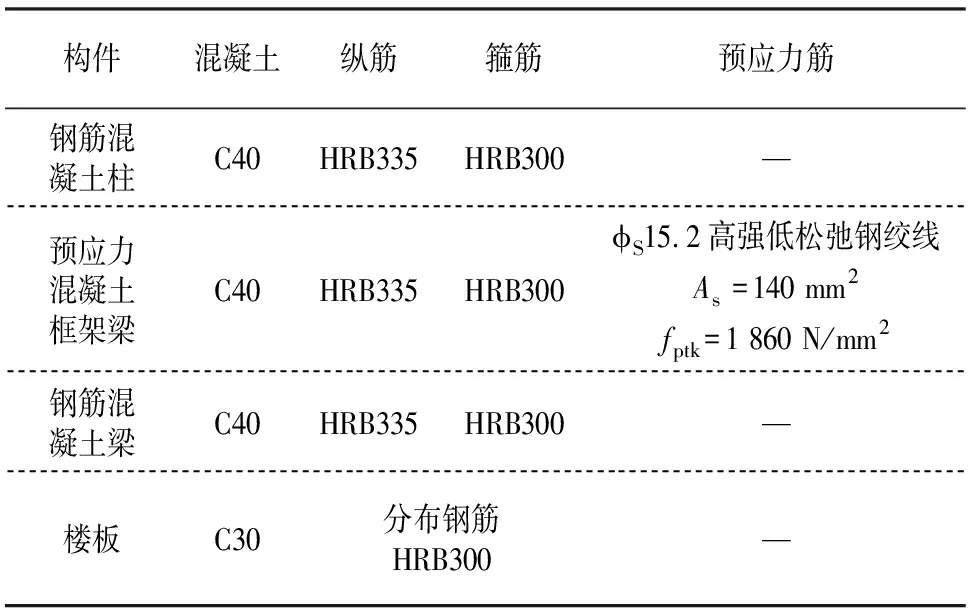
表2 结构材料信息
为充分发挥预应力钢筋的作用,一般将预应力筋布置在构件受拉一侧,本文所设计的预应力混凝土框架梁,其预应力钢束形状采用四段抛物线形,与框架梁受力后的弯矩图类似,如图1所示.

表3 结构荷载信息
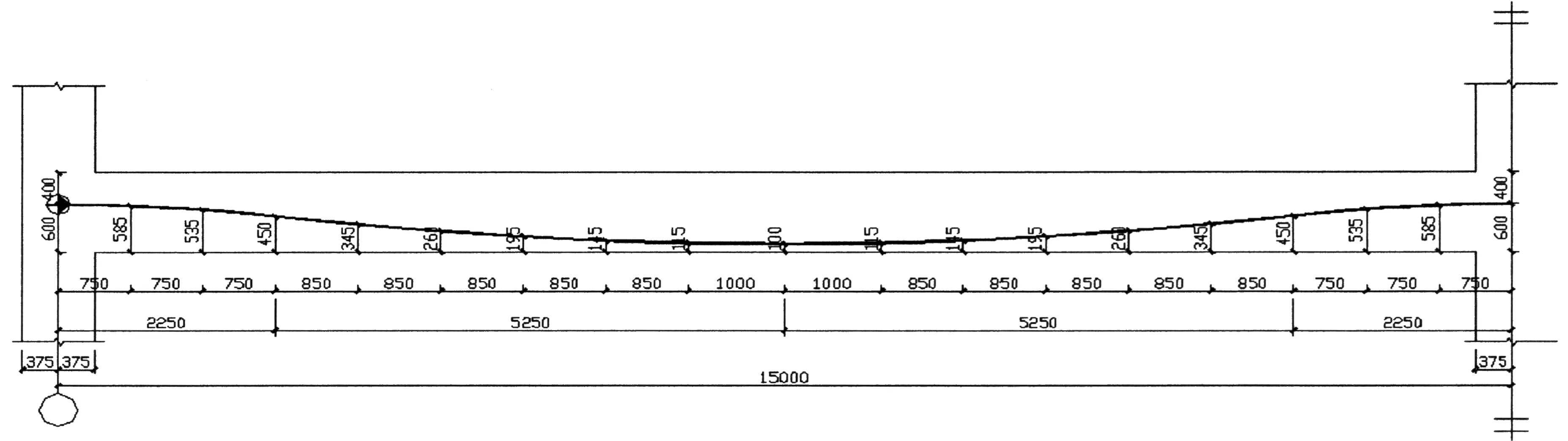
图1 预应力筋线形布置示意图(mm)
6个框架结构的基本设计原则是:首先根据01规范 (柱端弯矩增大系数为1.2)设计预应力框架结构KJ01;再根据04规程 (柱端弯矩增大系数取值,中柱为1.2,边柱为1.4)设计出框架KJ02;而后,以KJ02为基础,逐渐增大边柱和中柱的柱端弯矩增大系数设计出另外4个框架结构KJ03~KJ06,详见表4.
结构的平面布置及主要构件截面尺寸,见图2及图3.
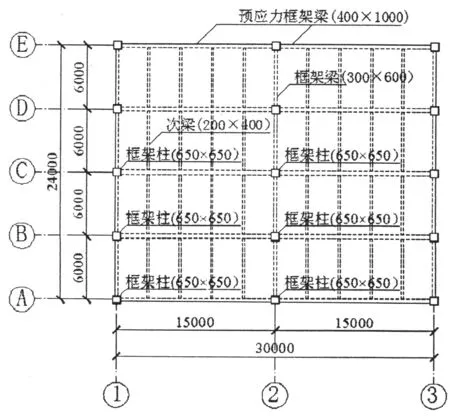
图2 结构平面布置示意图(mm)
经计算与验算,6个框架的预应力度、裂缝宽度、扰度、轴压比等均满足相关规范与规程的要求,各框架柱的配筋信息,见表5;框架梁配筋示意图、支座截面及跨中截面信息参见图4,梁底通长钢筋为6C25+2C22,梁顶通长钢筋为2C25,支座处负筋为8C25,分两排放置,跨中截面的梁顶钢筋由2C25的受力钢筋与2C14的架立钢筋组成,预应力钢绞线为15Фs15.2按图1的形式沿梁长布置.

图3 结构构件尺寸示意图(mm)
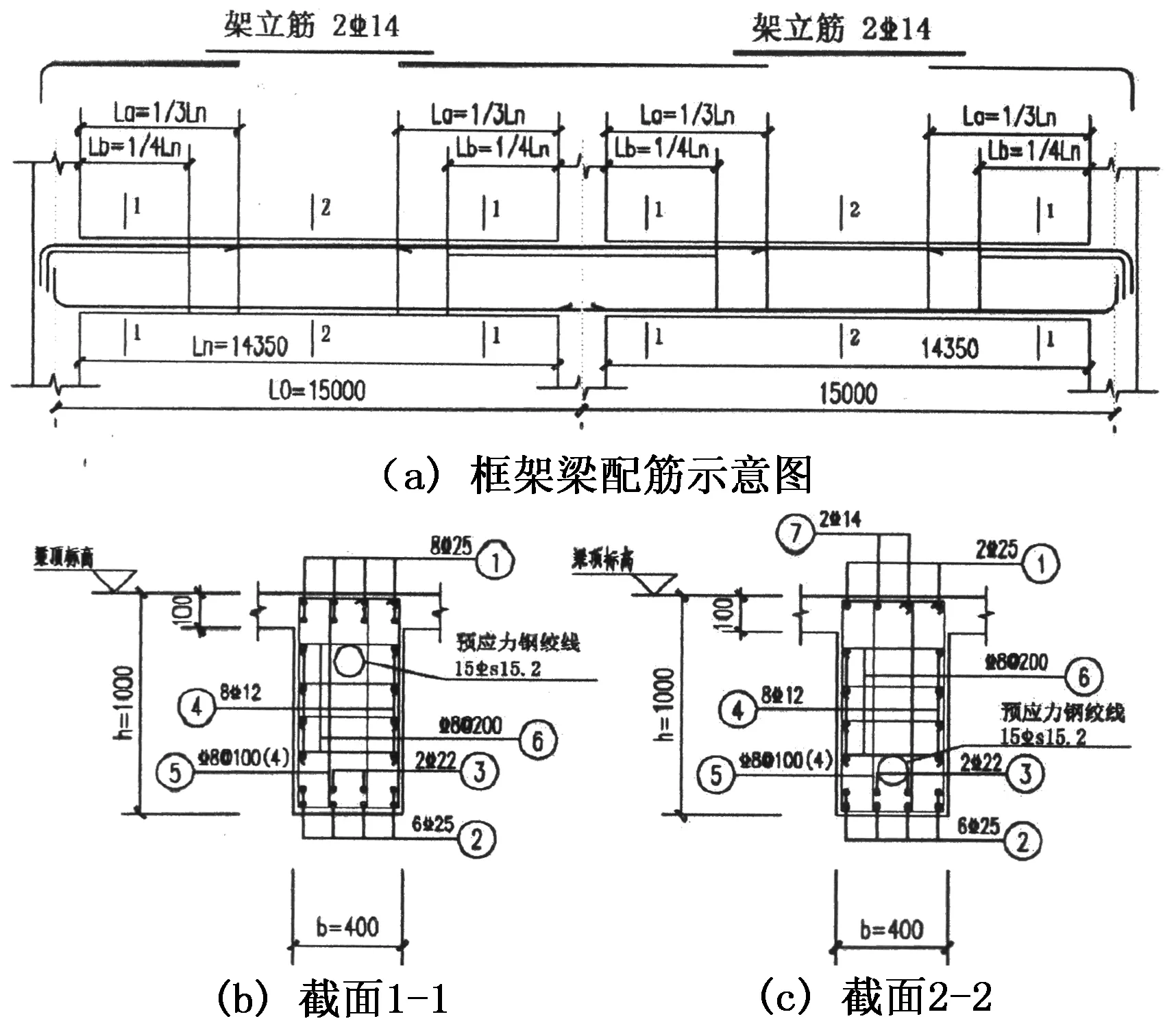
图4 框架梁配筋图(mm)
2 预应力框架结构的静力弹塑性分析
针对所设计的6个预应力混凝土框架结构,分别选取其中间榀平面框架,在SAP2000和PERFORM-3D中建模,并对其进行静力弹塑性分析.
2.1 结构的弹塑性分析模型
预应力混凝土框架的梁、柱构件采用局部纤维铰单元来模拟,即在梁端设置精度较高的纤维铰单元,以充分考虑钢筋与混凝土的弹塑性受力性能,其他部分则采用线弹性单元,以提高运算速度,如图5所示.
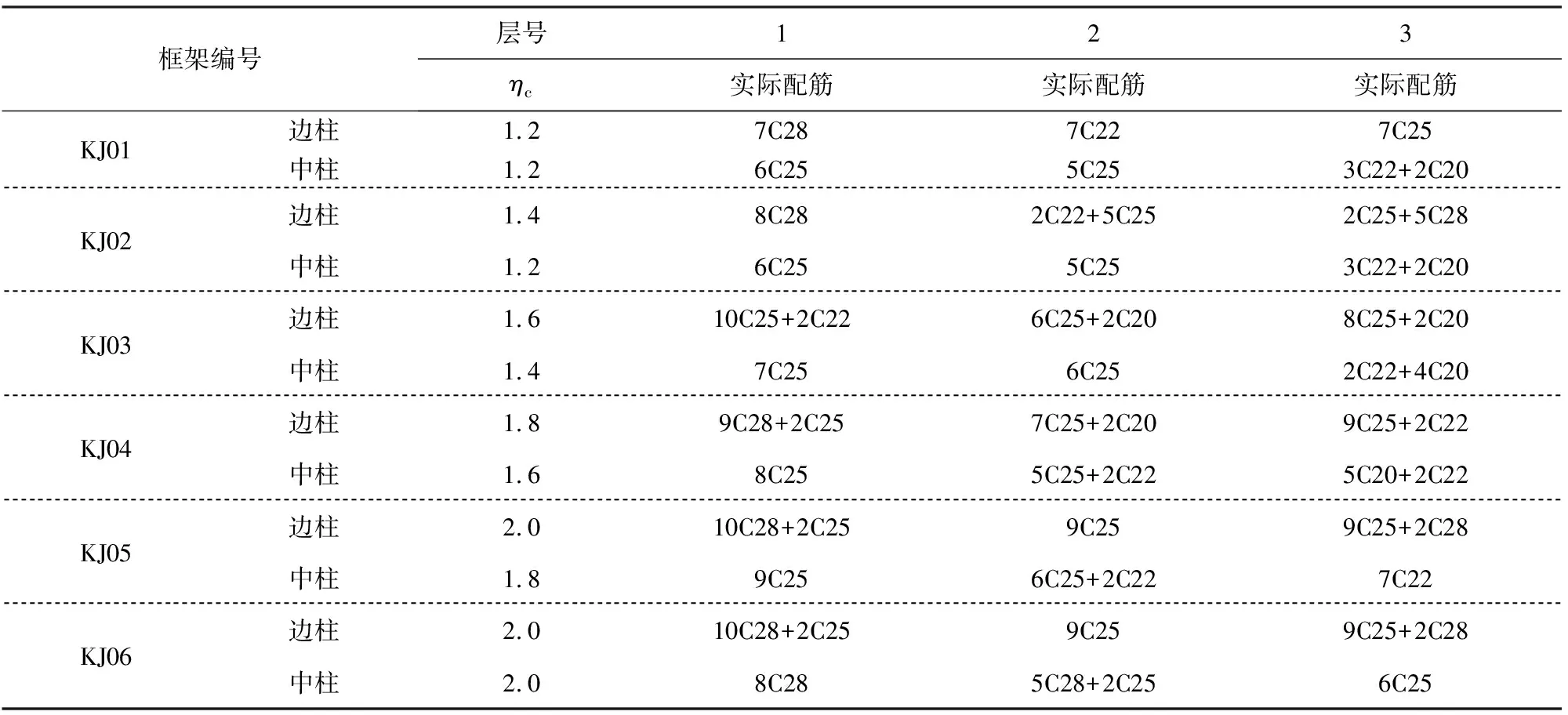
表5 KJ01~KJ06柱配筋情况

图5 局部塑性铰梁单元示意图
2.1.1 混凝土的本构模型
框架梁柱截面上的混凝土可分为保护层混凝土和核心混凝土,如图6所示.对于保护层混凝土,其本构模型采用程序中自带的普通混凝土模型,而核心混凝土的本构模型选用Mander[9-13]模型.

图6 混凝土截面示意图
2.1.2 钢筋的本构模型
在预应力混凝土结构中钢筋可分为普通钢筋与预应力钢绞线两类.在SAP2000[14-15]中,考虑钢筋的弹塑性性能,将普通钢筋的受力过程分为弹性区,弹塑性区及硬化、软化区3个部分,将预应力钢绞线的受力过程分为弹性区与塑性区,两种材料的骨架曲线见图7.

(a)普通钢筋骨架曲线

(b)预应力筋骨架曲线
在PERFORM-3D[16]中,钢筋的非线性本构模型包含拉-压钢筋模型、抗拉钢筋模型与考虑屈曲的钢筋模型3种,本文采用考虑了强度损失与应变能力的拉-压钢筋模型,以便更好地模拟结构中纵向钢筋的受力性能,其骨架曲线和滞回曲线,如图8所示.
2.1.3 预应力筋预应力效应的模拟
在 PERFORM-3D中,预应力筋的作用效应是通过对预应力混凝土梁构件施加等效荷载来模拟的.在SAP2000中,预应力效应可模拟为预应力钢束单元或等效荷载.为了使两种软件在建模方法上保持一致,将力筋预应力效应均模拟为等效荷载.

(a)钢筋骨架曲线

(b)钢筋滞回曲线
2.1.4 结构动力特性
本文分别在两种软件中对结构进行模态分析,限于篇幅,下面仅列出KJ01前三阶周期,并与PKPM的计算结果进行对比,见表6.
由表6可知,预应力混凝土框架结构在PKPM,SAP2000及PERFORM-3D中的周期信息吻合良好,这在一定程度上表明,本文所建立的预应力混凝土平面框架结构的分析模型是正确的.

表6 SAP2000、PERFORM-3D与PKPM计算的KJ01前三阶周期
2.2 结构的静力弹塑性分析与讨论
在SAP2000与PERFORM-3D中,分别对6个框架进行静力弹塑性分析,采用能力谱法求取结构的性能点,其分析流程如图9所示.

图9 能力谱法分析流程
2.2.1 框架能力曲线
下面给出 KJ01~KJ06 6个平面框架结构的PUSHOVER曲线及对比图,见图10、图11.
从图9可以看出:根据不同弯矩增大系数设计的预应力混凝土框架,在SAP2000与PERFORM-3D中均能顺利地进行静力弹塑性分析,在两个软件中所得到的能力曲线(基底剪力-顶点侧移曲线),在走势上是十分吻合的,这也进一步验证了本文所建立模型的正确性.
由图11可以发现:各框架的能力曲线都有十分明显的卸载阶段,随着柱端弯矩增大系数的增加,结构能力曲线中峰值的基底剪力不断增加;由图11(a),SAP2000中KJ01的峰值基底剪力约为1 620 kN,KJ06的峰值基底剪力约为1 800 kN,由图11(b),PERFORM-3D中KJ01的峰值基底剪力约为1 450 kN,KJ06的峰值基底剪力约为2 000 kN;在推覆作用后期,能力曲线下降阶段随着柱端弯矩增大系数的增加而逐步推迟,结构的延性具有一定的提高,但并不明显.
2.2.2 框架结构的性能点
限于篇幅,仅列出 KJ01~KJ06在PUSHOVER中性能点的顶点位移与基底剪力(见表7),结构性能点的具体求取过程未予给出.图12为各框架层侧移曲线,图13为各框架层间位移角曲线.
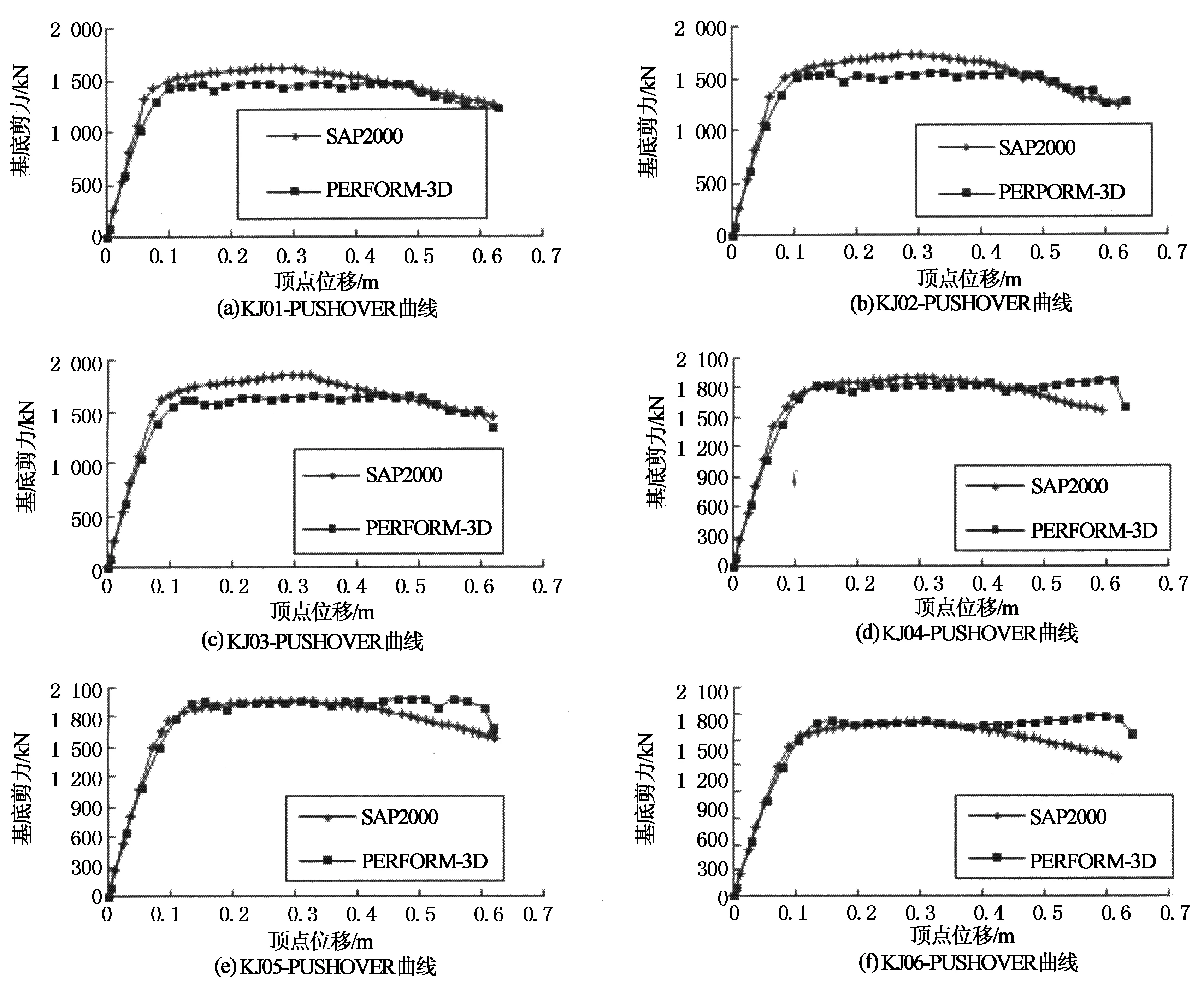
图10 KJ01~KJ06的能力曲线

图11 SAP2000与PERFORM-3D中各框架的能力曲线对比

表7 KJ01~KJ06性能点基底剪力与顶点位移值
由表7可以看出:随着柱端弯矩增大系数的增大,结构的基底剪力具有较大幅度的增加,而顶点位移也不断在增大.
由图12和图13可以看出:各个框架的层间位移角均满足抗震规范对于框架结构弹塑性层间位移角不得超过1/50的规定;结构的底层为薄弱层; KJ01及KJ02的底层层间位移角远小于1/50,有较大的储备能力空间,这表明04规程和01规范中对于柱端弯矩增大系数的规定,能够保证预应力混凝土框架结构在罕遇地震作用下不发生倒塌破坏.随着柱端弯矩增大系数的增大,第一层的侧移与层间位移角变化不大,结构第二层和第三层的侧移与层间位移角都逐渐增大,这说明柱端弯矩增大系数的增加,对于改善结构底层层间位移的效果不明显.

图12 SAP2000与PERFORM-3D中各框架层侧移曲线

图13 SAP2000与PERFORM-3D中各框架层间位移角曲线
2.2.3 构件塑性铰分布情况与结构屈服机制
图14与图15为KJ01~KJ06塑性铰转动量及屈服机制的分析结果.
由图14与图15可以看出:在SAP2000和PERFORM-3D中,6个PC框架结构构件端部的塑性铰分布图基本一致,表明6个结构的屈服机制是大致相符的;按照01规范和04规程所设计的KJ01与KJ02,其底层中柱柱脚破坏十分严重,其塑性铰转动量已大于0.006,底层中柱柱顶也同时出铰,其转动量约为0.003,底层边柱柱脚与二层部分中柱的柱底、柱脚的塑性铰转动量均超过0.004而出铰,其它各层梁端均有出铰,但梁端转动量的最大值远不如柱端大,结构形成了以柱端出铰为主,底层中柱的柱顶、柱脚同时出铰的梁柱铰屈服机制;随着柱端弯矩系数的逐渐增大,当边柱取1.8,中柱取1.6时(见图15中KJ04),结构底层中柱柱脚与一层梁端产生的塑性铰基本一致,均在0.005左右,形成了梁、柱同时出铰的梁柱铰屈服机制;当框架边柱取2.0,中柱取1.8或2.0时,一层梁端的塑性铰转动量超过了各层柱端的塑性铰转动量,各层柱的柱脚、柱顶未同时出铰,形成了以梁端出铰为主的梁柱铰屈服机制,达到了预应力混凝土框架较为理想的屈服机制.
通过以上分析,可以得到以下结论:
1)结构的整体抗震性能.依据04规程和01规范设计的预应力混凝土框架结构,基本上可以满足8度区罕遇地震作用下的抗震要求,柱端弯矩增大系数的增加对改善预应力混凝土框架的整体抗震性能并没有明显帮助.
2)结构的局部抗震性能.依据04规程和01规范设计的预应力混凝土框架结构底层柱出铰十分严重,柱端弯矩增大系数的增加对减少预应力混凝土框架柱的塑性铰转角、增加预应力梁端出铰具有显著的效果.
3) 结构屈服机制.依据04规程和01规范设计的预应力混凝土框架结构,在罕遇地震作用下,形成以柱端出铰为主,底层中柱柱顶、柱脚同时出铰的屈服机制,对抗震不利;随着柱端弯矩增大系数的逐渐增大,结构屈服破坏机制表现出明显改善,当边柱的ηc取1.8、中柱的 取1.6时,形成梁、柱同时出铰的梁柱铰屈服机制;当边柱的ηc取2.0、中柱ηc取1.8时,结构形成以梁铰为主的梁柱铰屈服机制,这是有利于结构抗震的机制.
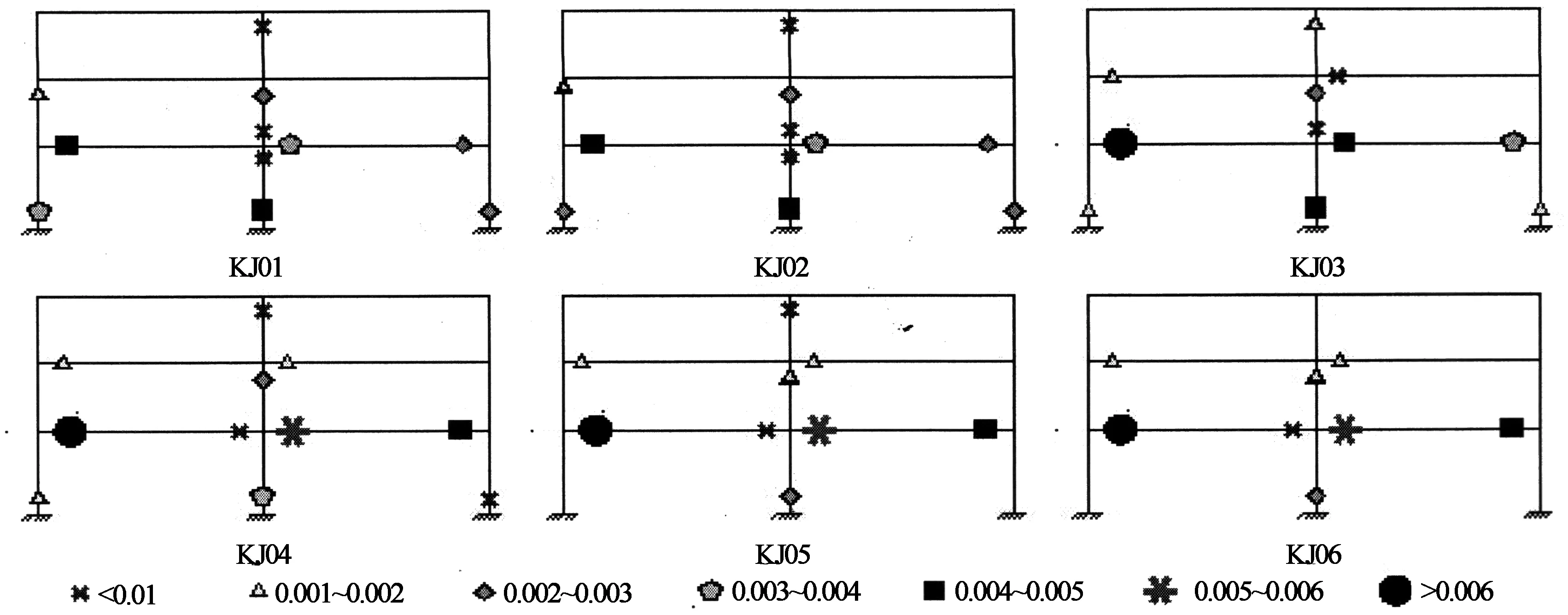
图14 SAP2000中KJ01~KJ06的塑性铰分布
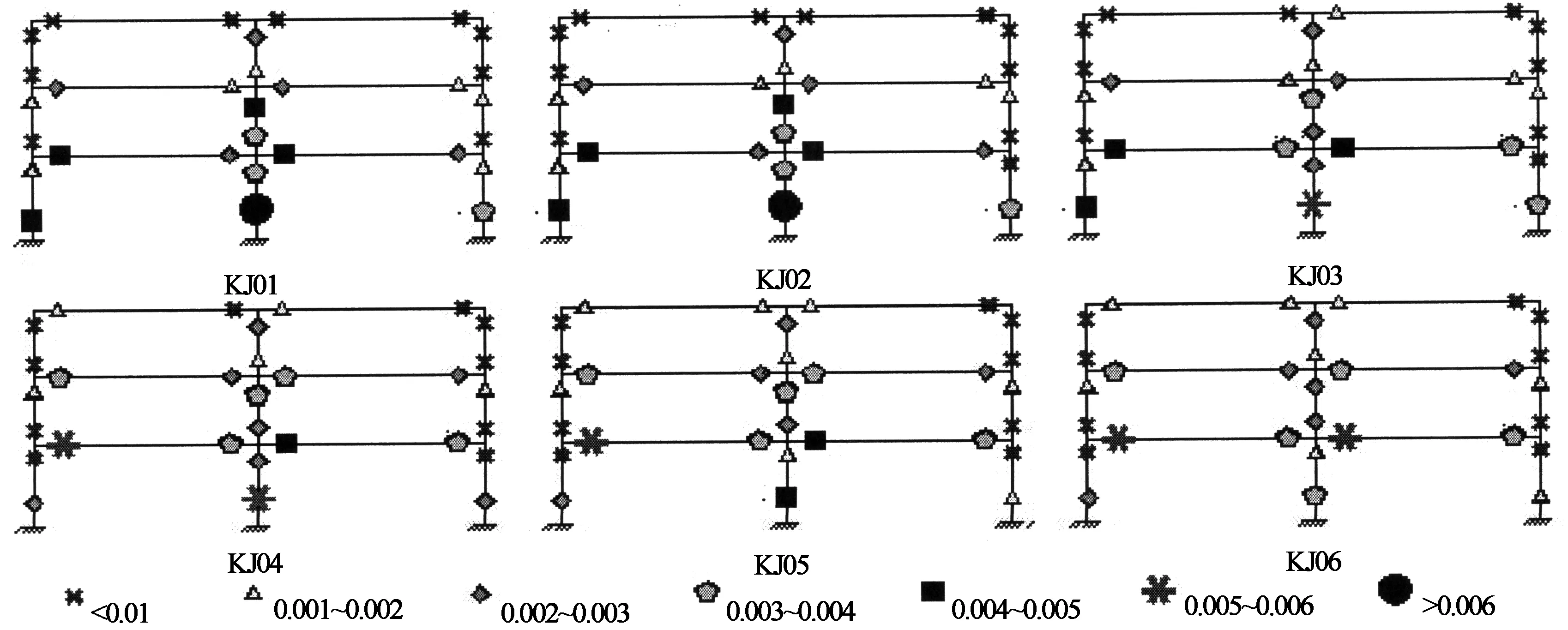
图15 PERFORM-3D中KJ01~KJ06的塑性铰分布
3 动力弹塑性时程分析
为进一步探讨预应力混凝土框架结构柱端弯矩增大系数对框架结构抗震性能的影响,本文在PERFORM-3D中,对框架KJ01~KJ06进行动力弹塑性时程分析.
3.1 阻尼及地震波的选取
在动力弹塑性分析中,结构的阻尼采用Rayleigh阻尼.在地震波选择时,根据规范要求,选用两组实际强震记录与一组人工波模拟的加速度时程曲线,利用意大利SeismoSoft公司研发的SeismoMatch[17-18]与SeismoArtif[19]程序进行地震波的选择与人工波的拟合,见表8,各地震波相应的地震加速度时程曲线见图16,各地震波相应的加速度反应谱与结构设计时所用的设计地震反应谱对比曲线见图17.由地震波加速度反应谱与结构设计地震反应谱比较可看出:本文所选择的3条地震波,在理论上与频谱匹配的选波原则是十分吻合的.
3.2 预应力混凝土框架的动力弹塑性分析结果及讨论
3.2.1 楼层侧移
图18为各框架楼层最大侧移曲线图及各框架楼层最大侧移平均值曲线图.由图可以看出,Chi-Chi地震波作用下各楼层侧向位移的变化,不如Friuli地震波与RG-(4)的变化明显.

表8 天然波与人工波信息记录

图16 地震波加速度时程曲线
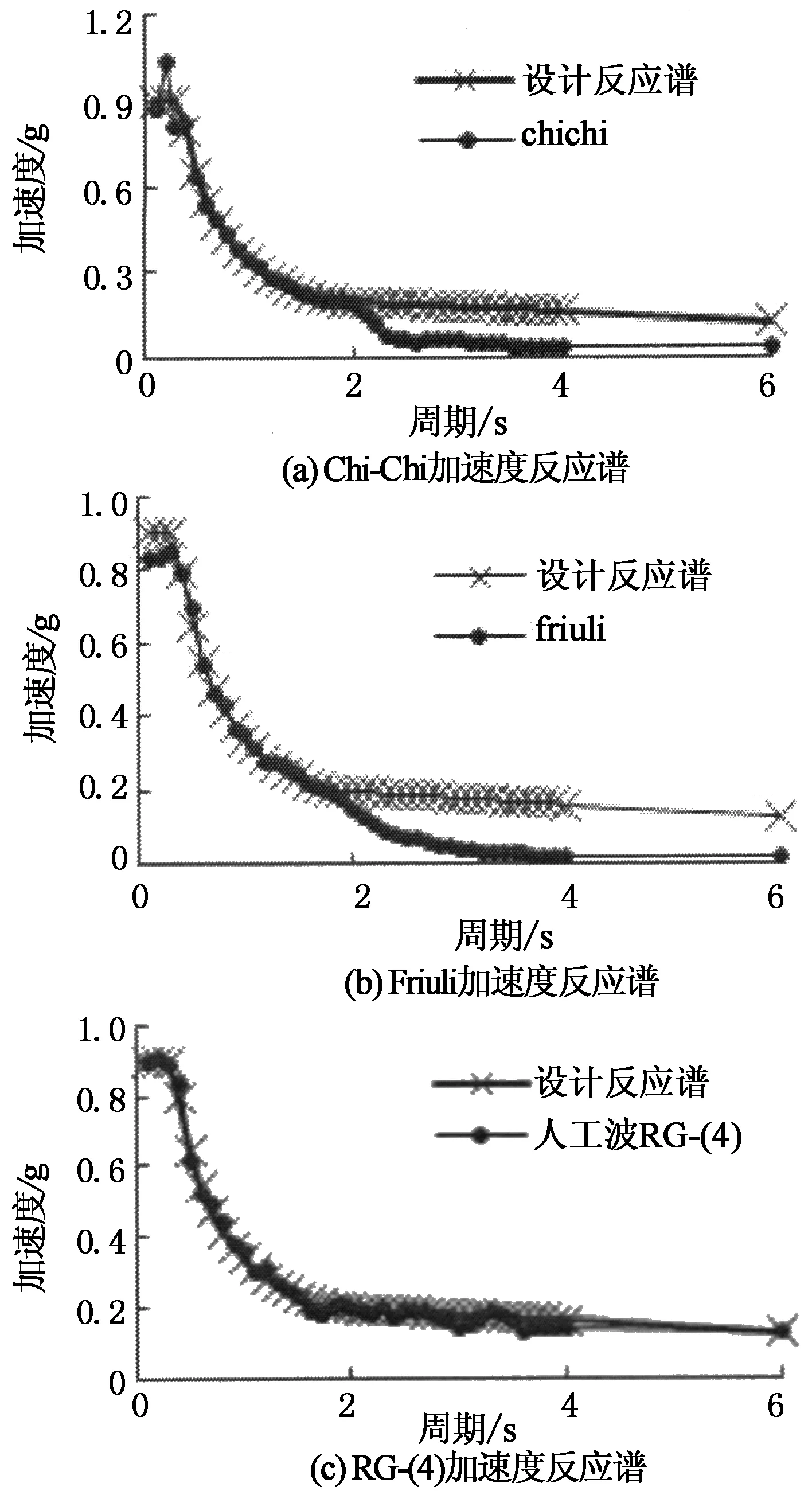
图17 地震波加速度反应谱曲线

图18 结构的侧向位移曲线
3.2.2 层间位移角
图19为6个框架楼层最大层间位移角曲线图及各框架楼层最大层间位移角平均值曲线图.由图可以看出:本文所有预应力混凝土框架结构的层间位移角,均满足建筑结构抗震规范中框架弹塑性层间位移角限值1/50的规定;各框架一层层间位移角最大,即显示出预应力混凝土框架底层为薄弱层;随着柱端弯矩增大系数的增加,框架的各楼层最大层间位移角总体呈增长趋势,但其增长的幅度很小,说明按照规范中柱端弯矩增大系数取值设计的预应力混凝土框架,能够保证结构在8度区罕遇地震作用下不至于倒塌.此外,增大柱端弯矩增大系数,对预应力混凝土框架结构底层先破坏、底层为薄弱层的现状以及结构整体的抗震性能并没有改善作用.

图19 结构的层间位移角曲线
3.2.3 塑性铰信息
表9列出了KJ01~KJ06各框架一层梁端、边柱及中柱塑性铰转角最大值.
由表9可以发现:按照规范设计的预应力混凝土框架KJ01与KJ02,其第一层梁端的塑性铰转角为0.004左右,底层边柱柱底出铰严重(0.006)、柱顶未出现明显出铰(0.0018),底层中柱柱底(0.007)、柱顶(0.004)均发生较为明显的出铰,形成了以柱端出铰为主的梁柱铰混合出铰的屈服机制,并且,其中柱的柱底、柱顶均发生严重出铰,对抗震极为不利.随着柱端弯矩增大系数的逐渐增加,梁端的塑性铰转角逐渐增大,而底层边柱、中柱柱底塑性铰转角均有明显减小,当边柱ηc取2.0,中柱ηc取1.8时(如KJ05),梁端塑性铰转角大于柱端塑性铰转角,底层中柱柱顶转角为0.002,为刚刚出铰状态,KJ05和KJ06的破坏形式,均为以梁端出铰为主的梁柱铰混凝土出铰屈服机制,而且,同一根柱柱顶、柱底不同时出铰,有利于抗震.

表9 各框架构件塑性铰转角最大值
通过在PERFORM-3D中对KJ01~KJ06进行动力弹塑性时程分析,得到以下结论:
1)结构的整体抗震性能:虽然经过了严格的地震波选择过程,地震波的随机性依然很大;依据04规程和01规范设计的预应力混凝土框架结构,基本上可以满足8度区罕遇地震作用下的抗震设计要求,柱端弯矩增大系数的增加对改善预应力混凝土框架的整体抗震性能并没有明显帮助.
2)结构的局部抗震性能及屈服机制:04规程和01规范设计的预应力混凝土框架结构底层柱出铰十分严重,增大柱端弯矩增大系数可以较好地改变预应力混凝土框架的屈服机制,当边柱ηc取2.0,中柱ηc取1.8时,结构形成以梁端出铰为主的梁柱铰混合出铰屈服机制,这是预应力混凝土框架较为理想的屈服机制.
综上所述,动力弹塑性时程分析结果与静力弹塑性分析的结论基本一致.
4 结 论
按照我国《预应力混凝土结构抗震设计规程》(JGJ 140-2004)和《建筑抗震设计规范》(GB 50011-2001),设计了6个2跨3层的预应力混凝土框架结构,采用局部纤维铰梁单元建模,在SAP2000与PERFORM-3D中分别对其进行了静力弹塑性和动力弹塑性分析,得到以下结论:
1)依据我国04规程和01规范设计的预应力混凝土框架结构,基本上能满足8度区罕遇地震作用下的抗震设防要求,但是,其结构底层柱出铰十分严重,形成以柱端出铰为主、底层为薄弱层,底层中柱柱顶、柱脚同时出铰的梁柱铰混合屈服机制,对框架结构抗震十分不利.
2)柱端弯矩增大系数的增加,对预应力混凝土框架底层为薄弱层的现状没有明显的帮助,但对结构屈服破坏机制有明显改善.因此,将04规程中预应力混凝土框架结构边柱及中柱的柱端弯矩增大系数进行适当的增加,有利于预应力框架结构大震时实现对抗震较为有利的屈服机制.
3)根据本文的分析结果,在对04规程进行修订时,针对不同抗震等级的预应力混凝土框架结构的柱端弯矩增大系数,建议给予适当的提高,二级框架结构的边柱ηc可取2.0,中柱ηc可取1.8.
[1] 张瀑, 鲁兆红, 淡浩. 预应力混凝土框架结构实用设计方法[M]. 北京:中国建筑工业出版社, 2012:1-11.
ZHANG Pu, LU Zhao-hong, DAN Hao. The practical design method of prestressed concrete frame structure[M]. Beijing:China Architecture & Building Press, 2012:1-11.(In Chinese)
[2] 薛伟辰. 现代预应力结构设计[M]. 北京:中国建筑工业出版社, 2003:1-3.
XUE Wei-chen. The design of modern prestressed structure[M]. Beijing:China Architecture & Building Press, 2003:1-3.(In Chinese)
[3] JGJ 140-2004 预应力混凝土结构抗震设计规程[S]. 北京:中国建筑工业出版社, 2004:17-18.
JGJ 140-2004 Seismic design procedures for prestressed concrete structure[S]. Beijing:China Architecture & Building Press,2004:17-18.(In Chinese)
[4] GB 50011-2001 建筑抗震设计规范[S]. 北京:中国建筑工业出版社, 2001:48-49.
GB 50011-2001 Code for seismic design of buildings[S]. Beijing:China Architecture & Building Press, 2001:48-49.(In Chinese)
[5] GB 50011-2010 建筑抗震设计规范[S]. 北京:中国建筑工业出版社, 2010:54-55.
GB 50011-2010 Code for seismic design of buildings[S]. Beijing:China Architecture & Building Press, 2010:54-55.(In Chinese)
[6] DOOLEY K L, BRECCI J M. Seismic evaluation of column-to-beam strength rations in reinforced concrete frames[J]. ACI, Structural Journal, 2001,98(6):843-851.
[7] ONO T,ZHAO Y, ITO T. Probabilistic evaluation of column overdesign factors for frames[J]. Journal of Structural Engineering, 2000, 126(5): 605-611.
[8] 管民生, 杜宏彪, 韩大建. RC矩形柱框架结构不同柱-梁抗弯强度比的Pushover分析[J]. 建筑结构, 2009, 39(4):14-42.
GUAN Min-sheng, DU Hong-biao, HAN Da-jian. Pushover analysis on rectangular column frames with different column to beam strength ratios[J].Buliding Structure, 2009,29(4):14-42.(In Chinese)
[9] 蔡健, 周靖, 方小丹. 柱端弯矩系数取值对RC框架结构抗震性能影响的评估[J]. 土木工程学报, 2007,40(1):6-14.
CAI Jian, ZHOU Jing, FANG Xiao-dan. Evaluation of influences of var ious moment magnifying coefficients at column ends of RC frames on seismic performance[J]. China Civil Engineering Journal,2007,40(1):6-14.(In Chinese)
[10]张耀庭, 马超, 郭宗明, 等. 不同弯矩增大系数钢筋混凝土框架结构地震易损性分析[J]. 建筑结构学报, 2014, 35(2):29-37.
ZHANG Yao-ting, MA Chao, GUO Zong-ming,etal. Seismic fragility analysis for RC frame structures with various moment magnifying coefficients[J]. Journal of Building Structures, 2014, 35(2):29-37.(In Chinese)
[11]SCOTT B D, PARK R, PRIESTLEY M J N. Stress-strain behavior of concrete confined by overlapping hoops at low and high strain rates[J]. ACI Journal, 1982,79(2):13-27.
[12]MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering, 1988,114(8):1804-1826.
[13]CHANG G A, MANDER J B. Seismic energy based fatigue damage analysis of bridge columns:part I—Evalualion of seismic capacity[R]. Buffalo, NY:National Center for Earthquake Engineering Research,1994:3-30-3-43.
[14]北京金土木软件技术有限公司. Pushover分析在建筑工程抗震设计中的应用[M]. 北京:中国建筑工业出版社, 2010:36-37.
Civil King Software. The application of pushover analysis in seismic design of building engineering[M]. Beijing:China Architecture & Building Press,2010:36-37.(In Chinese)
[15]北京金土木软件技术有限公司,中国建筑标准设计研究院. SAP2000中文版使用指南 [M]. 2版. 北京:人民交通出版社, 2012:71-73.
Civil King Software, China Institute of Building Standard Design & Research. SAP2000 Chinese version using guide[M]. 2nd.Beijing:China Communications Press,2012:71-73.(In Chinese)
[16]曾明. PERFORM-3D基本操作与实例[M]. 北京:中国铁道出版社, 2013:41-50.
ZENG Ming. Basic operation and projects of PERFORM-3D[M]. Beijing: China Railway Publishing House, 2013:41-50.(In Chinese)
[17]ABRAHAMSON N A. Non-stationary spectral matching[J]. Seismological Research Letters, 1992, 63(1): 30-39.
[18]HANCOCK J, WATSON-LAMPREY J, ABRAHAMSON N A,etal. An improved method of matching response spectra of recorded earthquake ground motion using wavelets[J]. Journal of Earthquake Engineering, 2006, 10: 67-89.
[19]GASPARINI D A, VANMARCKE E H E J. Simulated earthquake motions compatible with prescribed response spectra[M].Cambridge, MA:Massachusetts Institute of Technology, Department of Civil Engineering,1976:56-62.
