螺栓球网架节点高强螺栓的疲劳性能研究*
2014-09-18欧阳卿杜运兴聂逸悠
周 芬,欧阳卿,杜运兴,聂逸悠
(湖南大学 土木工程学院,湖南 长沙 410082)
目前,我国的网架结构规模处于世界前列.这种结构通常应用于大型的工业以及公用建筑中,一旦发生破坏将会造成安全事故和巨大的经济损失.在网架结构的破坏形式中疲劳破坏是一种脆性破坏,后果非常严重.《网架结构设计与施工规程》[1]中第1.0.4条规定“直接承受中级或重级工作制的悬挂吊车荷载并需进行疲劳验算的网架构件,其疲劳强度应进行专门的试验确定.”《钢结构设计规范》[2]中第6.1.1条规定“直接承受动力荷载重复作用的钢结构构件及其连接,当应力循环次数大于或等于5×104次时,应进行疲劳计算.”网架结构疲劳通常发生在节点位置,网架节点有焊接球节点和螺栓球节点两种,关于焊接疲劳计算的文献较多,其中彭凡[3]采用临界距离理论评定了焊接接头的疲劳寿命.由于螺栓球节点的研究相对较少,现行钢结构设计规范中的疲劳构件和连接分类中没有螺栓球节点这一类,工程技术人员在设计时仅能凭经验,存在一定的安全隐患.目前国内外已有学者对高强螺栓的疲劳性能进行研究,如太原理工大学的闫亚杰[4]、雷宏刚[5]等人已经对部分型号螺栓的疲劳性能进行了试验,得出了在不同应力差下螺栓的疲劳寿命,为螺栓的疲劳设计提供了一定的参考.本文将根据断裂力学理论并结合S-N曲线法对螺栓球节点中高强螺栓的疲劳性能进行进一步的研究.
1 高强螺栓的裂纹
1.1 高强螺栓的裂纹形式及其应力强度因子
裂纹是构件产生疲劳破坏的重要原因.裂纹的产生通常和应力集中有密切的关系,应力集中程度越高,裂纹萌生的几率也就越大.在螺栓球节点中高强螺栓在使用过程中存在着显著的应力集中.螺栓上应力集中最严重的部位是螺栓的螺纹根部,因此在该处最容易萌生裂纹.在裂纹出现之后该处的应力集中会进一步增大,进而裂纹也进一步发展.在螺栓球节点中高强螺栓上的应力集中并非沿着螺栓杆每个截面都是一样的,通常螺栓杆上与螺栓球最外边缘啮合的螺纹根部的应力集中最大,在该处产生的裂纹表现为表面裂纹.为了便于分析,本文将该裂纹按半圆形裂纹处理.由于螺栓球节点中的高强螺栓承受的是拉力,故该裂纹属于张开型表面裂纹.
《应力强度因子手册》[6]中规定,用于描述圆柱体的张开型表面裂纹的应力强度因子可表示为:
(1)
(2)
(3)
式中:KⅠC为圆柱的应力强度因子;S为构件上的名义应力;a为裂纹的长度;λ为a/d,d为圆柱体直径;α1为圆柱体形状系数;
目前对于螺栓螺纹处张开型表面裂纹的应力强度因子研究得比较少.沈阳航空工业学院的尹峰等[7]通过试验得出:当裂纹深度达到一定值时,可忽略原本螺纹应力集中的影响,且螺纹原本应力集中影响与裂纹扩展深度呈线性关系.本文参照圆柱体的张开型表面裂纹的应力强度因子计算公式(1),对其进行修正获得螺栓的表面张开型裂纹的应力强度因子,见式(4):
(4)
式中:KⅠS为螺栓的应力强度因子;α2为螺栓形状系数.
对于螺栓来说,由于螺纹根部存在应力集中,该处裂纹的应力强度因子必定大于圆柱体表面张开型裂纹的应力强度因子.本文偏于安全地假定:当裂纹深度扩展到螺栓直径时才可忽略原本螺纹的应力集中影响.此时的应力强度因子与圆柱体的相同.当螺栓表面裂纹长度为0时,该处的应力为名义应力S乘以应力集中系数Kt,而圆柱体在裂纹长度为0时截面应力分布均匀.因此当裂纹长度为a0时,KⅠS=KtKⅠC.当裂纹开始扩展后,螺纹原有应力集中对螺栓应力强度因子的影响逐步降低.因此:
(5)
式中:Kt为裂纹出现前螺栓螺纹的应力集中系数;各型号螺栓的应力集中系数见表1.

表1 各型号螺栓的应力集中系数
1.2 高强螺栓的临界裂纹
由于缺乏有关40Cr钢断裂韧性的资料,采用与40Cr材料相近的34CrNi3Mo钢的断裂韧性代替[5].与34CrNi3Mo钢相比,40Cr钢材的强度稍高,但是韧性较低.查得34CrNi3Mo的断裂韧性为77.531 MPa·m1/2.
当螺栓裂纹扩展到一定程度时,螺栓会在循环荷载中的最大应力作用时断裂.此时应力强度因子K1CS等于材料的断裂韧性.将40Cr的断裂韧性代入式(4),得到式(6):

(6)
对式(6)进行化简,得到高强螺栓裂纹的临界长度为:
(7)
1.3 裂纹的扩展与疲劳寿命
疲劳裂纹形成之后,构件中的裂纹扩展首先按照与拉应力成45°角的最大剪应力方向扩展,之后裂纹开始沿最大拉应力方向扩展.对于这个阶段裂纹的扩展速率,近年来国内外学者进行了大量的研究.在众多研究结果中,Forman等人提出下述表达式考虑的因素较为全面,如式(8)所示:

(8)
(9)
式中:▽KⅠS为螺栓应力强度因子幅;Smin为最小名义应力,如为压力时取Smin=0;Smax为最大名义应力;a为裂纹的长度;C,m为实验测得的材料常数.
当初始裂纹为a0时,螺栓的疲劳寿命可表示为式(10):
(10)
查应力强度因子手册可知,40Cr钢的C=2.65×10-11,m=2.5.
由于螺栓螺纹根部存在很大的应力集中,故在该处容易萌生裂纹.且在应力集中的作用下裂纹萌生所需的循环次数大幅减少.对于螺栓而言,其裂纹扩展寿命在疲劳寿命中占有很大比重.因此本文在估算螺栓的疲劳寿命时只考虑裂纹扩展寿命.由于钢构件在冶炼加工中存在着初始缺陷,通常裂纹长度小于0.5 mm的钢构件为合格,因此一般情况下的工程估算假设初始裂纹a0=0.5 mm.
2 高强螺栓的疲劳寿命估算
2.1 高强螺栓的疲劳极限强度
一般情况下N=1对应的疲劳强度是材料的静拉伸强度Sb,由于钢材属于延性材料,故估算时所需要的Sb取螺栓的屈服强度.N=107时对应的疲劳强度是材料的疲劳极限.特别地,在应力比ρ=-1的情况下,S记为S-1.以M24高强螺栓为例,取Kt=5.46,联解式(4),(7)和(10)并取ρ=-1,N=107,a0=0.5 mm,经计算可以解得疲劳极限强度Sf=37 MPa.
由于不同型号螺栓的应力集中系数大致相当,可以算出其他型号螺栓的疲劳极限强度也都处于37~41 MPa之间.可以认为各型号螺栓的疲劳极限强度也大致相当.因此将37 MPa作为ρ=-1时各种型号螺栓的疲劳极限强度.
2.2 材料应力疲劳的特性及等寿命曲线
反映外荷载和疲劳寿命关系的曲线称为S-N曲线.典型的S-N曲线一般可分为3个部分.低周期疲劳区(LCF),高周期疲劳区(HCF)和亚疲劳区(SF).特别地,在应力比ρ=-1的情况下,S记为S-1.大量实验证明,在高周期区域(HCF)对数坐标下的S-N曲线近似为一条直线.S-N曲线存在多种表达式, 其中最为常用的是幂函数形式,本文也采用该形式估算螺栓的疲劳寿命.
幂函数形式:
N·Sα=C.
(11)
两边取对数有: lgN=A+BlgS.幂函数的S-N关系在对数坐标系上为直线.其中α和C为材料常数,Sf为应力疲劳极限.
反映材料特性的S-N曲线是在给定应力比的情况下得出的.为了综合考虑应力幅和应力比的影响,可以将不同应力比情况下由实验得出的等寿命点画在Sa-Sm图上即为等寿命曲线.由于实验测等寿命曲线比较困难,故实际工程中常采用一些估算等寿命曲线的经验模型.其中Goodman模型[8]偏于保守,为工程实际中常用.
Goodman直线模型:
(12)
式中:
Sa=(Smax-Smin)/2,
(13)
Sm=(Smax+Smin)/2.
(14)
式中:Smax为最大名义应力;Smin为最小名义应力.
2.3 基于S-N曲线法的螺栓疲劳寿命估算
根据《钢网架螺栓球节点用高强螺栓》[9]中规定,10.9级高强螺栓的屈服强度应不小于940 MPa.
因此N=1时,S-1=Sb=940 MPa.lgS-1=2.973 1;N=107时,S-1=Sf=37 MPa,lgS-1=1.568 2.
因此在采用幂函数表达式的情况下,高强螺栓的双对数坐标S-N估算曲线如图1所示.
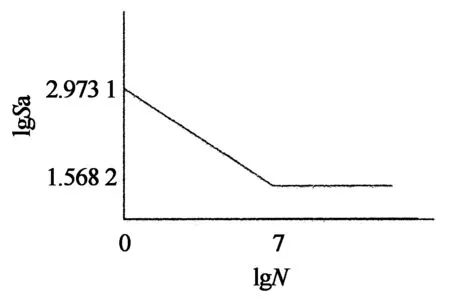
图1 高强螺栓的S-N双对数坐标曲线图
将其表达式简化后可以得到:
lgN=14.813-4.983lgSa.
(15)
为了将多种应力比情况下的应力疲劳关系在同一条S-N曲线中表示,本文借助等寿命曲线将不同应力比下的Sa全部等效为在应力比为-1时的S-1.再将S-1替代Sa后得到:
lgN=14.813-4.983lgS-1.
(16)
式中:
(17)
由于《钢结构设计规范》(GB 50017)中所规定直接承受动力荷载重复作用的钢结构构件及其连接,当应力循环次数大于或等于5×104次时,应进行疲劳计算.由式(17)中可以得出,此时的S-1=107 MPa.因此可以认为当直接承受动力荷载重复作用且循环次数大于或等于5×104次时的螺栓球节点连接,螺栓上的S-1≤107 MPa.此外《钢结构设计规范》(GB 50017)中规定的容许应力幅对应疲劳寿命是2×106次,同样可以由式(17)得出,此时的S-1=51 MPa.因此也可以认为当螺栓上S-1≤51 MPa时的螺栓以球节点连接时,可不进行疲劳计算.
2.4 估算公式与实验结果的比对
为了验证高强螺栓疲劳寿命估算公式的计算精度,现将该公式的计算结果与国内现有的螺栓球节点常幅疲劳试验数据进行对比.
对比数据采用太原理工大学的闫亚杰[4]、雷宏刚等对螺栓球节点网架结构用M20,M30的10.9级高强螺栓进行了疲劳试验的结果.实验数据中有32组数据是对螺栓进行常幅循环加载,其中有9组螺栓的循环次数达到或超过了2×106次.另外有4组螺栓(第7,10,21和22组)由于存在不同程度的初始缺陷造成螺栓过早破坏,这些数据应该剔除.对比结果见表2.
由表中数据对比可知,除去4组存在初始缺陷的螺栓后,28组螺栓的估算值与理论值误差的平均值为0.544,均方差为0.582.其中有25组实验疲劳寿命高于估算疲劳寿命,另有3组(第9,19和20组)估算寿命略大于实验寿命.总体而言,估算结果还是偏于安全的.且在高周期疲劳的估算值与实验结果误差不大,当循环次数多于5×104次时的估算结果与实验结果误差大多在一倍以内,这在疲劳估算中是比较准确的.实验数据也证明当S-1≤51 MPa时螺栓球节点所经历的循环次数均大于2×106次.如图2所示.
此外还可以发现,当应力水平较高、循环次数较少时,螺栓疲劳的实验寿命高出估算寿命较多.如第1组到第6组,疲劳的实验寿命均高出估算寿命的10倍左右,这是由于加载的最大应力较高,在缺口效应的作用下使得螺栓螺纹根部出现了塑性区,从而缓解了应力集中,使疲劳寿命大幅提高.且对于循环次数较低的疲劳构件,其寿命的离散率也更高.
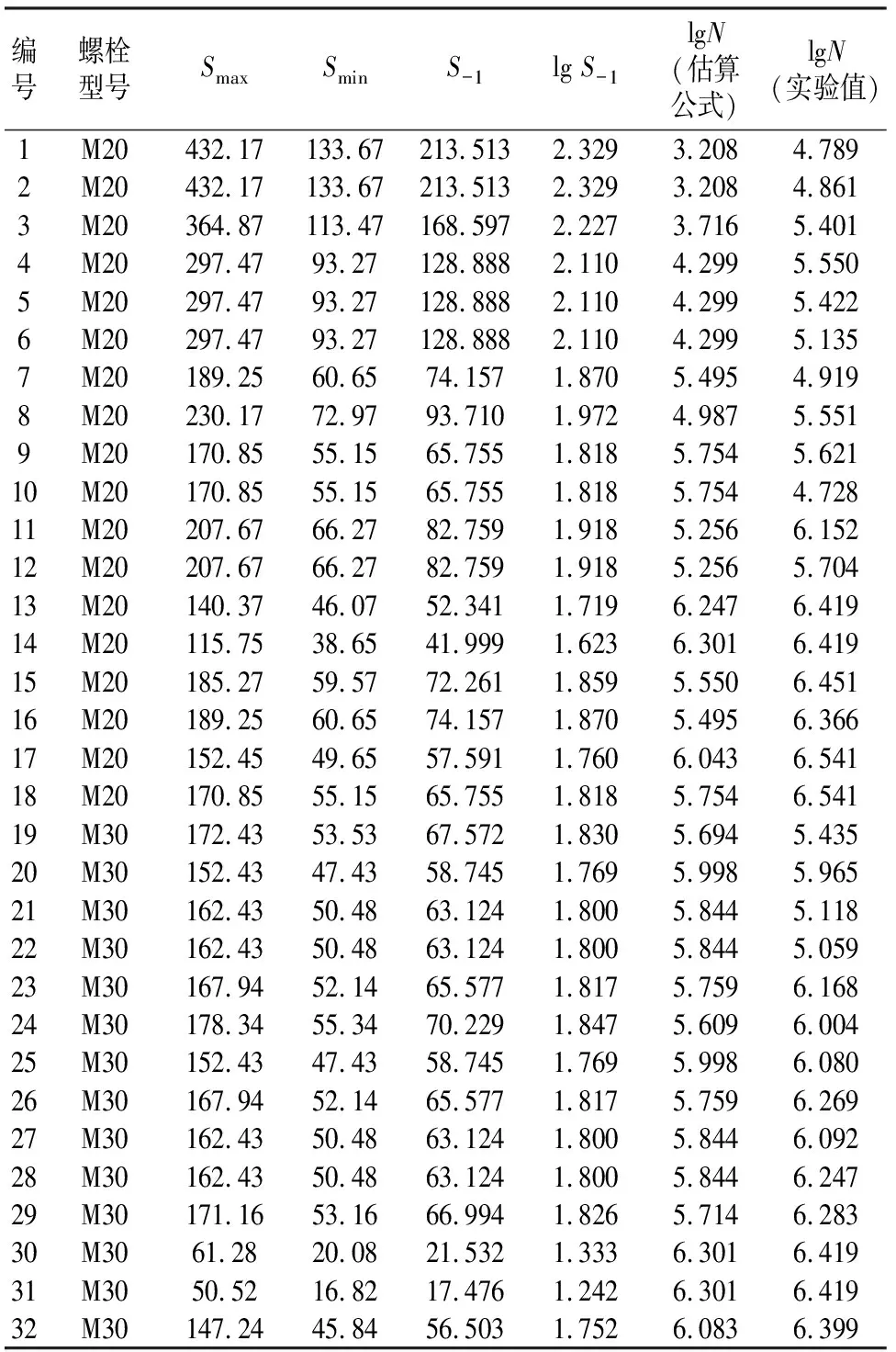
表2 估算寿命与实验寿命对比
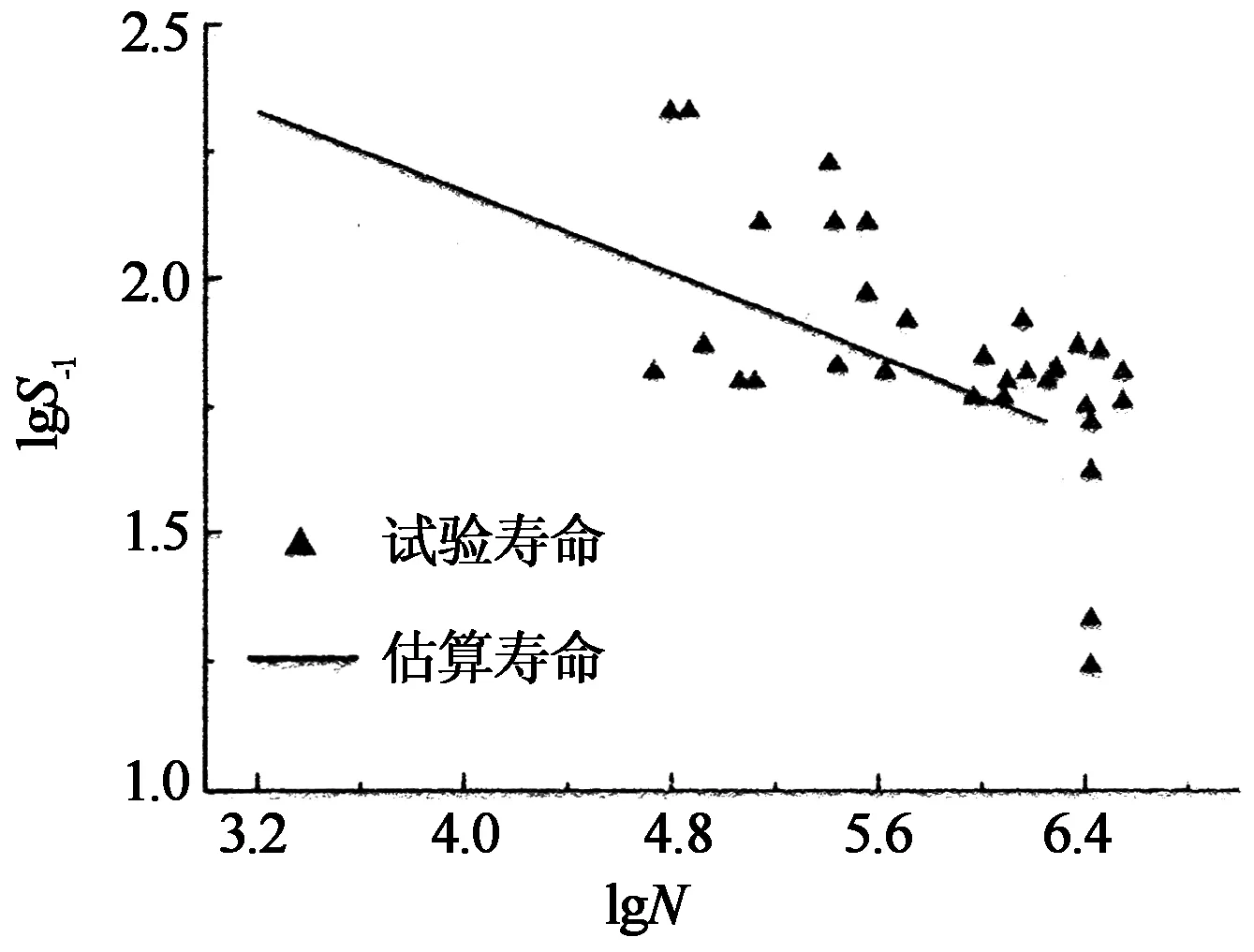
图2 估算寿命与试验寿命的S-N双对数坐标对比
2.5 初始裂纹对疲劳性能的影响
实际构件中存在的缺陷是多种多样的,对于高强螺栓而言与螺栓球啮合的第一圈螺纹根部的表面张开型裂纹最危险.
为了对比不同长度初始裂纹对高强螺栓疲劳性能的影响,本文采用式(4),(7)和(10)并取a0=1.0 mm与1.5 mm所计算出的N与实验数据进行对比,结果见表3.
由于本文所采用的计算方法只适用于高周期疲劳(N≥104),故当计算N<104时,取N=0,当N≥2×106时,取N=2×106.

表3 a0=1.0 mm,1.5 mm时疲劳估算寿命与实验寿命对比
对比表中的估算寿命可发现,裂纹对螺栓的疲劳性能影响很大.且裂纹长度越短,其扩展速率越快.因此准确测得裂纹长度才能保证螺栓的疲劳性能.由表中数据可知,当a0为1 mm时,螺栓的疲劳寿命约为实验寿命的25%,当a0为1.5 mm时,螺栓的疲劳寿命约为实验寿命的10%.
3 结 论
提出了螺栓球网架节点高强螺栓的疲劳性能计算方法并进行了疲劳性能研究,获得了如下成果:
1)采用本文所提出的高强螺栓疲劳寿命计算方法所得到的结果与试验结果相比基本吻合,大多数螺栓的疲劳估算寿命较实验寿命数值小,偏于安全.当应力水平较低时,采用本文的高强螺栓寿命估算结果与实验结果较接近,高周期疲劳的估算寿命与实验寿命相差在一倍左右.这是由于应力水平较高的螺栓螺纹根部塑性区较大,使螺栓的疲劳性能得到提高,估算寿命常不及实验寿命的10%.
2)比较了高强螺栓裂纹长度对高强螺栓的疲劳性能的影响.随着高强螺栓裂纹长度的增加,会大大减少高强螺栓的疲劳寿命.当裂纹长度超过1 mm时,高强螺栓的计算疲劳寿命大约降至没有裂纹螺栓试验结果的1/4.
[1] JGJ 7-91网架结构设计与施工规程[S]. 北京:中国建筑工业出版社, 1991:1-3.
JGJ 7-91 Space truss design and construction regulations[S]. Beijing: China Architecture and Building Press,1991:1-3. (In Chinese)
[2] GB 50017-2003 钢结构设计规范[S]. 北京: 中国计划出版社, 2003: 68-70.
GB 50017-2003 Code for design of steel structures[S]. Beijing:China Plan Press, 2003:68-70. (In Chinese)
[3] 彭凡, 姚云建, 李良中. 临界距离理论评定焊接接头疲劳寿命的研究[J]. 湖南大学学报:自然科学版, 2012, 39(5):28-32.
PENG Fan, YAO Yun-jian, LI Liang-zhong. Study of critic distance theory on the fatigue assessment of welded joints[J]. Journal of Hunan University: Natural Sciences, 2012, 39(5):28-32.(In Chinese)
[4] 闫亚杰,雷宏刚,焦晋峰,等. 螺栓球节点网架结构中高强度螺栓常幅疲劳计算方法的建立[J].建筑结构学报,2010,31(S1): 92-97.
YAN Ya-jie, LEI Hong-gang, JIAO Jin-feng,etal. Constant amplitude fatigue calculation method of high strength bolts in grid structures with bolt sphere joints[J]. Journal of Building Structures, Supplementary Issue,2010, 31(S1):92-97. (In Chinese)
[5] 雷宏刚. 螺栓球节点网架结构高强度螺栓连接疲劳性能的理论与试验研究[D]. 太原: 太原理工大学建筑与土木工程学院, 2008:56-128.
LEI Hong-gang. The theoretical and experimental research on fatigue performance of high strength bolt connection in grid structure with bolt sphere joint [D]. Taiyuan:College of Architecture and Civil Engineering, Taiyuan University of Technology, 2008: 56-128. (In Chinese)
[6] 中国航天研究院.应力强度因子手册[M].北京:科学出版社, 1993:297.
China Academy of Space. Stress intensity factor handbook[M]. Beijing: Science Press, 1993:297.(In Chinese)
[7] 尹峰, 魏玉霖, 刘欣. 受拉螺栓表面裂纹应力强度因子的估算[J]. 沈阳航空工业学院学报,1994 (27):14-20.
YIN Feng, WEI Yu-lin, LIU Xin. Evalation of surface crack in the thread groove of bolts subjected to axial tension loading[J]. Journal of Shenyang Institute of Aeronautical Engineering, 1994(27): 14-20. (In Chinese)
[8] LEGUILLON D, QUESADA D, PUTOT C,etal. Prediction of crack initiation at blunt notches and cavities-size effects[J]. Engineering Fracture Mechanics, 2007, 74(15): 2420-2436.
[9] GB/T 16939-1997钢网架螺栓球节点用高强度螺栓[S]. 北京: 中国计划出版社, 1997:5.
GB/T 16939-1997 High strength bolts for Joints of space grid structures[S]. Beijing: China Plan Press, 1997:5. (In Chinese)
