弹性地基复合曲梁抗弯力学性能研究

郝扣安, 王振清, 周利民, 王欣

(1.哈尔滨工程大学 航天与建筑工程学院，黑龙江 哈尔滨 150001；2.香港理工大学 机械工程系，香港；3. 上海宇航系统工程研究所，上海 201109)

复合材料凭借其优越的使用性能、结构和功能的可设计性，成为航空航天、汽车、船舶等众多产业的首选材料之一。实际工程结构中，对曲面结构复合材料的需求是不可避免的，如倒角、对T型连接的加固等等。截至目前，针对弯曲结构梁的研究还大多集中于实验[1]和数值分析[2]。其中，Pagano[3-4]利用线弹性理论研究了多层复合材料层合板，并给出了在承受柱形弯曲状态下的精确解。然而，他考虑的是平板复合材料层合板承受横向载荷的情况。Lekhnitskii[5]给出了各向异性弯曲梁在力矩载荷下的通解。该方法同样也为ASTMD6415[6]采纳用于计算弯曲梁四点弯曲实验中层间拉伸应力。Shenoi[7]和李永胜[8]建立了基于弹性体弯曲梁弯曲行为的模型，得到了各向异性梁的弹性解。高阶剪切变形理论[9-10]可对跨厚比大于4的板壳结构，精确的计算面内变形和应力，但无法计算复合材料板壳的层间应力。

本文通过给定适当的边界条件和位移应力协调方程，利用弹性地基作用下的曲梁应力解，确定了平面内正应力中性轴的位置，推导出由2种不同材料组成的层合曲梁应力解。计算了不同几何外形、不同材料比例和材料参数对于曲梁层间正应力和平面内正应力大小、铺层顺序的影响。

1 曲梁的弹性基础模型

1.1 基本方程

李永胜等[8]考虑了弹性地基作用下的曲梁抗弯性能，如图1所示，单位宽度的曲梁被放置于模量为E的弹性地基上。其中，曲梁的内径为Ri，外径为Ro。假设弹性地基的反作用力垂直于曲梁表面，且与曲梁每点处的挠度v成正比。

(a) 几何外形

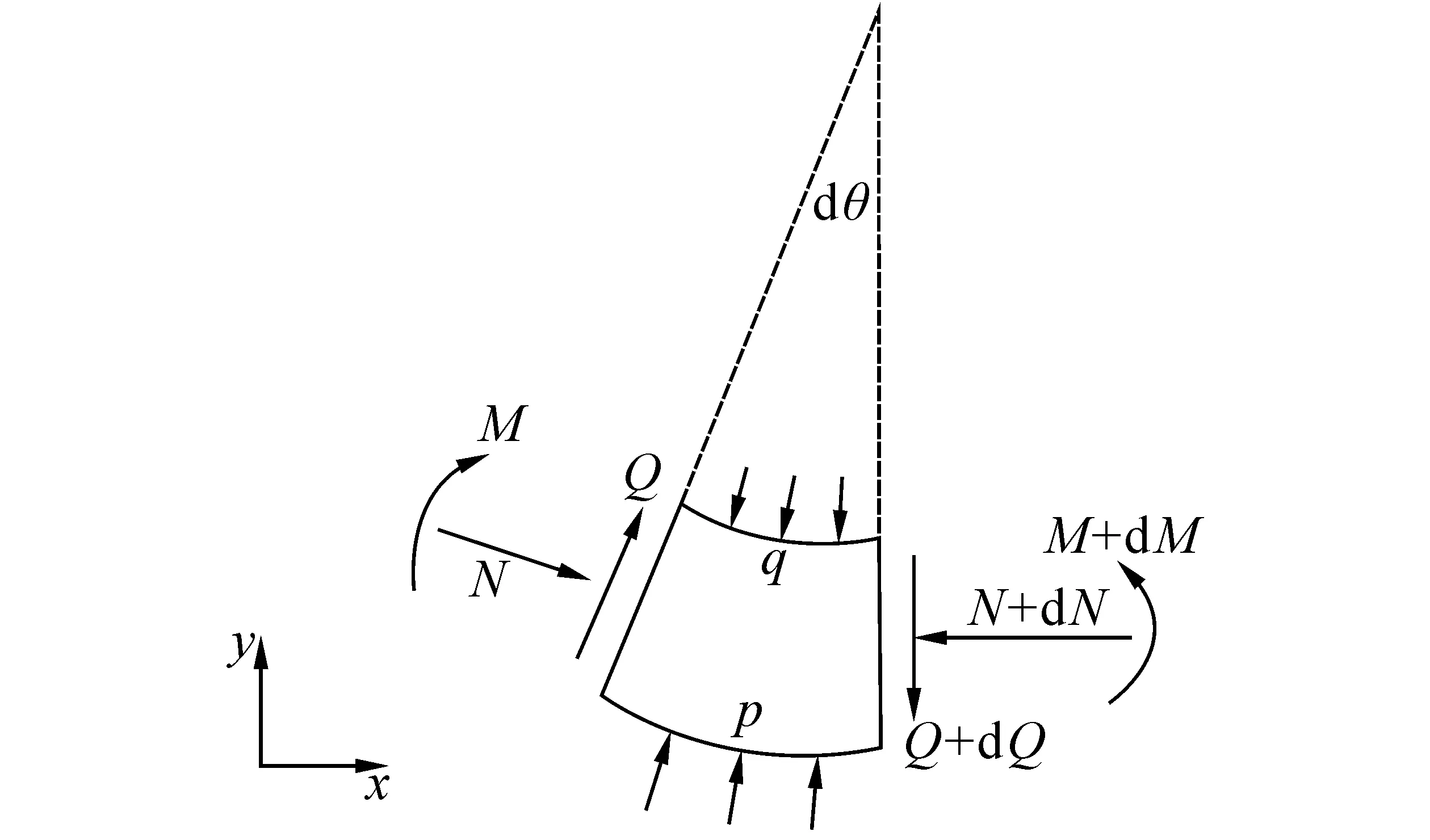
(b) 单元受力情况

(1)

曲梁的平衡方程有[7]：

(2)

为求解上式微分方程，需要建立力矩Mx与曲率变化κx的关系。对于复合材料层合板，二者的关系可由经典层合板理论[11]得出：

(3)

式中，

式中：Aij为拉伸刚度，Bij为拉弯耦合刚度，Dij为弯曲刚度，ε0为层合板几何中心处的应变，κ为曲梁的曲率变化。对于弯曲结构来说，力矩Mx与曲率变化κx的表达式需要考虑拉弯耦合、弯扭耦合。

仅考虑x方向的曲率变化，由式(3)可得：

(4)

(5)

纯弯曲载荷下，应力分量与θ角度无关，且有τrθ=0。

对于各向异性材料，有协调方程[13]：

(6)

求得应力分量：

(7)

式中：λ=Eθ/Er,为材料的周向与径向弹性模量之比；C2、C3和C4为常数，可通过给定边界条件求得。

1.2 边界条件

由图1(b)，有边界条件：

(8)

将式(7)中的各应力分量代入边界条件，式(8)中第3式可自动满足，可求得C2、C3和C4，故可求得应力分量表达式[7]：

(9)

2 基于弹性地基的复合曲梁模型

2.1 基本假设

在对复合曲梁分析之前，给出几点假设：

1)复合曲梁是由线弹性或各向异性材料组成，其材料主轴方向与整体坐标系方向一致；

3)不考虑自由边界效应 (Free-edge effects)；

4)弯曲梁中心线处的半径与弯曲梁厚度之比RG/t皆足够大以保证应变得以线性分布。

2.2 中性轴位置的确定

本文讨论矩形截面的复合曲梁，该复合曲梁(见图2)，由两种材料组成。图2同时还给出了复合材料横截面的几何参数，靠近外径部分为第一种材料，用I表示；靠近内径处的第2种材料，用II表示。复合曲梁的厚度为t，其中I层材料的厚度为tI，II层材料的厚度为tII。

图2 复合曲梁横截面尺寸

(10)

式中：r′为受到外力载荷后该点处的半径，δ为中心轴与中性轴之间的距离。

由正向力N与弯曲力矩M所产生的正应力施加于中心轴z轴处，可得平衡方程如下：

(11)

复合曲梁由两部分组成，I层曲梁和II层曲梁。结合式(10)，对式(11)进行变量替换，得：

(12)

由此可得：

(13)

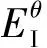
联立式(13)中两个方程，求得

(14)

2.3 复合曲梁应力求解

对于平面各向异性材料平面应变问题而言，Hooke's定律表达为[14]：

(15)

考虑极坐标中的几何方程：

(16)

(17)

(18)

(19)

同时，考虑边界处径向、周向位移连续，有边界条件如下：

(20)

因此，结合边界条件式(18)～(20)，可求得复合曲梁厚度方向的层间正应力与平面内正应力。

3 讨论与分析

3.1 内外径之比对曲梁应力的影响

针对单一材料的弯曲梁结构，根据式(9)考察内外径之比(Ri/Ro)对于层间正应力与平面内正应力的分布的影响。如果内径Ri=6.4 mm，M=1 000 N·m，图3分别给出了Ri/Ro= 0.2、0.4、0.6、0.8曲梁应力分布情况，图中对横坐标进行无量纲处理，为(r-Ri)/(Ro-Ri)。

(a) 层间正应力分布

(b) 平面内正应力分布

观察图3(a)发现，4条曲线的层间正应力最大值都位于偏离几何中心轴靠近内径处，而内外径之比不仅影响弯曲梁层间最大正应力值的大小，对于层间最大正应力值的相对位置也有影响。随着Ri/Ro的升高，层间最大正应力值降低，同时其位置逐渐向几何中心轴靠近。由图3(b)可知，随着Ri/Ro的升高，平面内最大正应力值也升高，而平面内正应力中性轴相对位置几乎不变。周向径向弹性模量之比λ对于应力分布无明显影响[7]。

3.2 材料参数对中性轴位置的影响

图4 不同周向模量比的中性轴位置随χ的变化情况

3.3 材料参数、体积比对复合曲梁应力的影响

针对材料II，考虑其体积含量对曲梁应力的影响，其中VII为材料II在曲梁结构中的体积百分比。

图5给出了VII为50%、60%、70%下对应的应力分布。作为比较，图中还给出了材料II曲梁(VII=100%)的应力分布,若Ri=6.4 mm，Ri=9.4 mm，M=1 000 N·m，其中I层II层材料参数由表1给出。

表1 复合曲梁材料参数

图5给出了II层材料体积百分比分别为50%、60%和70%的应力分布曲线。其中VII=100%时，最大层间正应力约为7.72 MPa，与文献[15]中7.60 MPa结果相近。

观察图5(a)，复合曲梁层间正应力分为2个明显区域，分界点横坐标与材料对应的体积百分比一致。从VII=100%到VII=50%，层间正应力最大值都位于II层内，且随着VII的增加而减小，且层间正应力最大值的位置越来越靠近复合曲梁内径。I层内的层间正应力最大值位于材料交界处，并沿着外径方向逐步减至零，随着VII的增大，I层内层间正应力最大值增大。

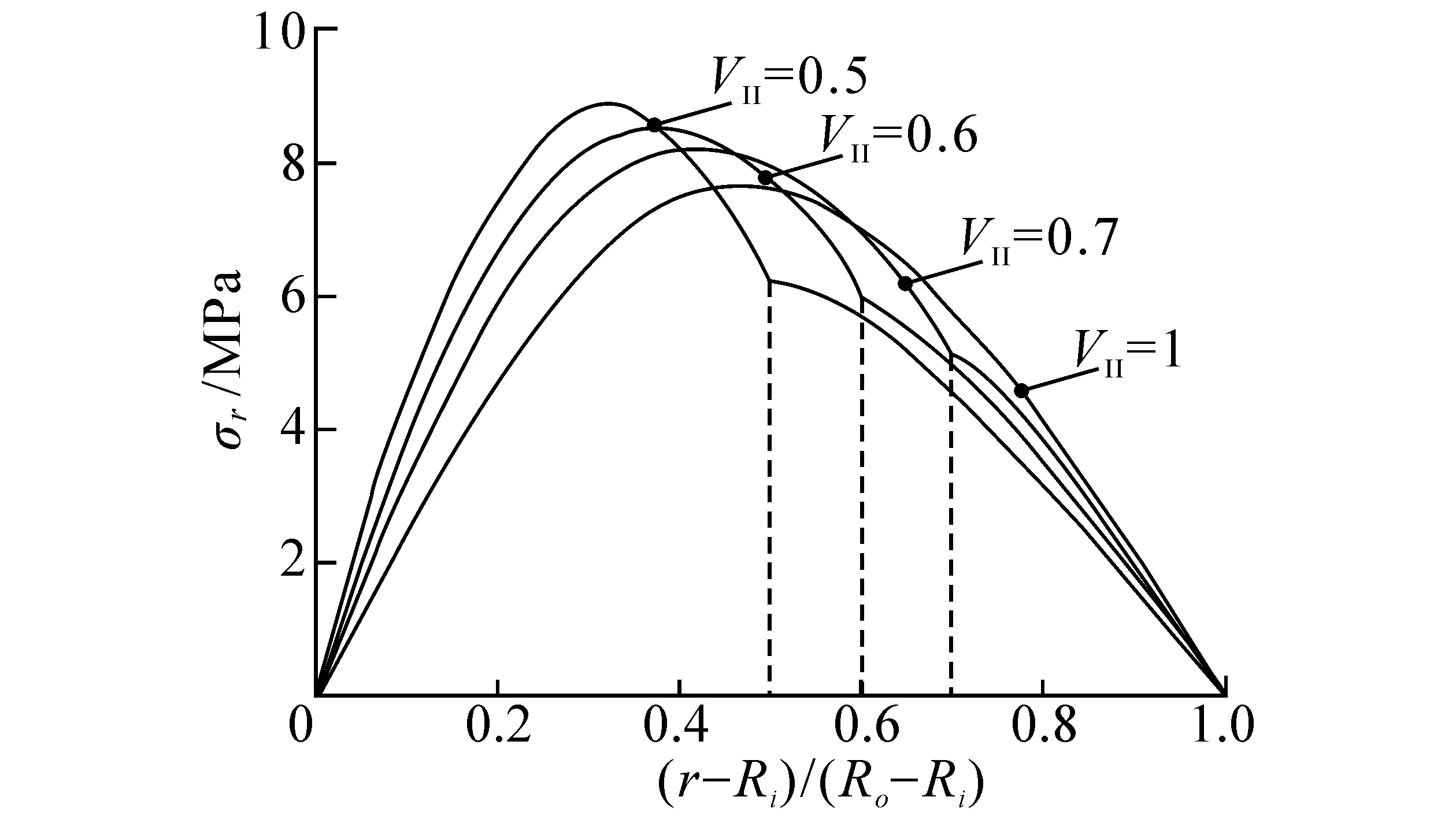
(a) 层间正应力分布

(b) 平面内正应力分布

观察图5(b)，2种材料不同周向弹性模量，复合曲梁平面内正应力存在明显的分界点，分界点与曲线对应的体积百分比一致。随着VII的减小，II层内的平面内正应力绝对值增大，而I层内的平面内正应力绝对值减小，其中性轴(平面内正应力为零)也向内径靠近。

本文将材料I、II位置互换，令材料II位于外径处，材料I位于内径处。图6中2种铺层顺序分别用实心点与空心点表示，给出了铺层顺序对应力分布的影响。

(a) 层间正应力分布

(b) 平面内正应力分布

观察图6(a)，2种铺层顺序的层间正应力的最大值都位于材料II区域内，当材料II靠近内径时，层间正应力最大值大于材料II靠近外径时。对于材料I来说，其区域内的层间正应力最大值也大于材料I位于外径处情况。观察图6(b)，其平面内正应力分布也呈现同样的趋势。

4 结束语

本文讨论了弹性地基作用下曲梁内外径之比(Ri/Ro)与其层间拉应力和平面内拉应力分布的关系。随着Ri/Ro的增大，层间拉应力最大值减小，最大拉应力位置逐步向几何中心轴靠近，平面内拉应力值也随之增大，而平面内拉应力的中性轴相对位置几乎不变。

在此基础上，分析了两层不同材料组成的曲梁，确定了平面内拉应力中性轴位置，给出了复合曲梁的层间拉应力和平面内拉应力解答，计算了不同几何外形、材料不同的体积分数和材料参数对于曲梁层间正应力和平面内正应力大小、铺层顺序的影响。

参考文献：

[1]TAN E L, UY B. Experimental study on curved composite beams subjected to combined flexure and torsion[J]. Journal of Constructional Steel Research, 2009, 65(8): 1855-1863.

[2]WANG W, SHENOI R A. Delamination modeling of a curved composite beam subjected to an opening bending moment[J]. Journal of Strain Analysis for Engineering Design, 2003, 38(5): 453-457.

[3]PAGANO N J. Exact solution for composite laminates in cylindrical bending[J]. Journal of Composite Materials, 1969, 3(3): 398-411.

[4]PAGANO N J. Analysis of the flexure test of bidirectional composites[J]. Journal of Composite Materials, 1967, 1(4): 336-442.

[5]LEKHNITSKII S G. Bending of a curved rod by moments and a force applied at the ends, theory of elasticity of an anisotropic body[M]. Moscow:Mir. Pub.，1981,

[6]ASTMD6415/D6415M-06a. Standard test method for measuring the curved beam strength of a fiber-reinforced polymer-matrix composite[S]. West Conshohocken: American Society for Testing and Materials, 1999.

[7]SHENOI R A，WANG W. Flexural behavior of a curved orthotropic beam on an elastic foundation[J]. Journal of Strain Analysis for Engineering Design, 2001, 36(1): 1-16.

[8]李永胜,王玮波,张效慈.考虑弹性地基的复合材料曲梁径向应力的研究[J].船舶力学, 2009, 13(4): 593-602.

LI Yongsheng, WANG Weibo, ZHANG Xiaoci. A study of through-thickness stresses in curved layered composite beams on a elastic foundation[J]. Journal of Ship Mechanics, 2009, 13(4): 593-602.

[9]LO K H, CHRISTENSEN R M, WU E M. Stress solution determination for high order plate theory[J]. International Journal of Solids Structure,1978, 14(8): 655-662.

[10]REDDY J R. A simple higher order theory for laminated composite plates[J]. Journal of Applied Mechanics, 1984, 51(12):745-752.

[11]SHENOI R A, WELLICOME J F. Composite materials in maritime structures, ocean technology series[M]. London:Cambridge University Press,1993.

[12]TOLF G. Stress in a curved laminated beam[J]. Fiber Science and Technology,1983,19:243-67.

[13]LU T J, XIA Z C,HUTCHINSON J W. Delamination of beams under transverse shear and bending[J]. Materials Science and Engineering, 1994, A188: 103-112.

[14]SHENOI R A, WANG W. Analytical solutions to predict flexural behavior of curved sandwich beams[J]. Sandwich Structures and Materials, 2004, 6: 199-216.

[15]SHENOI R A, WANG W. Through-thickness stresses in curved composites laminates and sandwich beams[J]. Composites Science and Technology,2001,61:1501-1512.