基于Modflow的岩溶管道概化与模拟探讨

肖 斌，许 模，曾 科，王 梅

(1.成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川成都610059;2.四川省地质环境监测总站，四川成都610084)

0 前言

岩溶介质在空间上的多尺度性决定了岩溶介质中地下水流态的多重性，岩溶介质的模拟概化是水文地质模拟上的一大难题。目前，对于多孔介质的模拟已经较为成熟，因此，在模拟岩溶介质时，国内外学者多采用等效连续多孔介质模型[1]。如Georgios Panagopoulps采用等效多孔介质模型模拟了希腊Trifilia地区岩溶含水层[2];毛邦燕等人运用等效多孔介质模型对不同型的岩溶介质进行分区概化[3]，都取得了较好的效果。但这种方法只适用于模拟范围大，岩溶发育程度较弱的含水层。对于含水层中存在对地下水具有强烈控制作用的大尺度(1～104 cm)岩溶管道[4]时，这种方法并不能对其进行有效的刻画。那么，能否在现有成熟的等效连续多孔介质模型的理论基础之上，找到一种恰当的对岩溶介质管道概化模拟的方法呢?笔者在本文中尝试利用三维有限差分地下水流动模型(Modflow)，寻求一种对于岩溶管道的合理概化，从而使得对强岩溶发育区地下水流的模拟更加合理、精确。

Modflow是由美国地质调查局的McDonald和Harbaugh开发出来的，基于连续多孔介质理论的地下水流模拟软件，其最显著的一个特点就是软件的模块化结构，即包括一个主程序以及若干相对独立的子模块。模块化的设计使得模型中各参数与边界条件的输入和修改相对独立，计算过程又能使模型各个单独的模块紧密的联系起来[5]。这种模块化的设计为我们寻求岩溶管道的概化方法提供了可能性。

1 Modflow中现有可用模块

目前，在Modflow的各个模块中，可以考虑用于概化模拟岩溶管道的有:单元渗流计算子模块(BCF)、排水沟子模块(DRN)、河流子模块(RIV)和溪流子模块(STR)。

1)单元渗流计算子模块(BCF)

在Modflow中，单元渗流计算子模块用于计算相邻单元之间的水力传导系数以及计算单元之间的地下水渗流量，也可以用于计算含水层由于贮水量的变化所吸收或释放的水量[5]。在实际应用中，是通过渗透系数(K)和贮水系数(S)的设置来实现的。在模拟强岩溶介质含水层时，可溶岩岩体中岩溶管道发育规模较小的部分，可根据实际钻孔抽水试验获得的数据进行赋值;而根据陈崇希的管道K值表式(1)，可将其中的大型岩溶管道部分赋值为由该式折算得出的渗透系数，贮水系数按100%孔隙率计算。

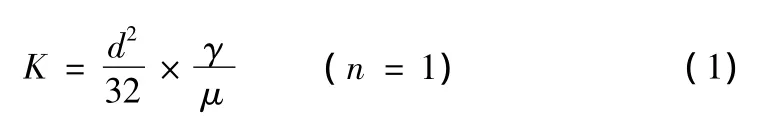
式中:K为岩溶管道渗透系数(LT－1);d为岩溶管道内径(L);γ为流体的重率(FL－3);μ为流体的动力粘度(FTL－2);n为空隙率(无量纲)[6，7，8]。

2)排水沟子模块(DRN)

在Modflow中，排水沟子模块原设计目的是模拟农用排水沟渠的排水效果。排水沟从含水层中排泄地下水，排水量正比于含水层的水头与排水沟的高程之差，其中要求含水层水头高于排水沟的高程，而当含水层水头低于该排水沟高程时，就不起排水作用[5]。图1表示某计算单元的横截面图，假定排水沟中仅部分有水，因而排水沟的水头大约等于其半高处的高程di，j，k。模型所计算的计算单元水头(hi，j，k)是计算单元的的水头平均值。排水沟的水头di，j，k只局限于沟渠之内而不是将其延伸至整个计算单元。在排水沟与含水层水头hi，j，k之间的区域，垂向面上存在辐射流或半辐射流，其特点一般为，越接近沟渠，水头梯度越大。在地下水流向排水沟过程中的水头损失是形成水头差hi，j，k－ di，j，k的原因。

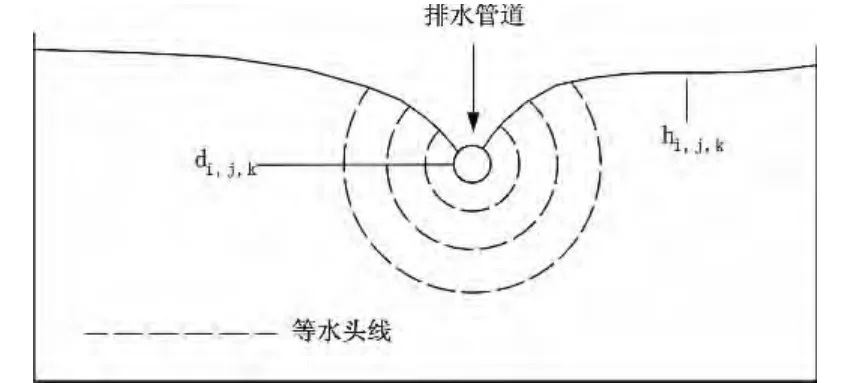
图1 排水沟计算单元(i，j，k)的汇聚水流之水头损失横剖面示意图

根据排水沟子模块的上述特性，可以将排水沟子模块应用于岩溶含水介质向岩溶管道排水的计算[9]，用以反映管道和含水介质间的水力交换。模型中，排水量正比于含水层水头与暗河管道高程之差，当含水层水头低于排水沟高程时，无排水效果[5]:

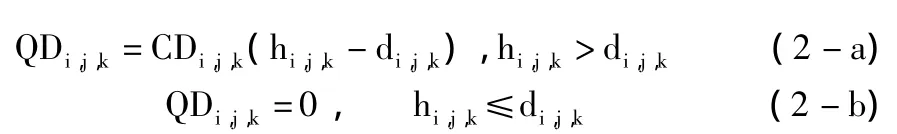
式中:QDi，j，k为排水沟排水量，CDi，j，k为等效水力传导系数，用于描述排水沟和计算单元(i，j，k)间的总水头损失。在岩溶介质的暗河管道附近岩体导水能力强，可以采用较大的等效水力传导系数反映岩溶管道快速排泄地下水的特点。

3)河流子模块(RIV)

在Modflow中，河流与溪流子模块是用来模拟地表水体对地下水流的影响，包括河流、溪流向地下水系统提供水，以及地下水系统向河流、溪流排泄地下水，具体是补给还是排泄取决于河流单元与相邻单元地下水之间的水力梯度。河流子模块在模型中模拟其与含水层计算单元(i，j，k)之间的水力联系时由下面一套方程来实现[5]:

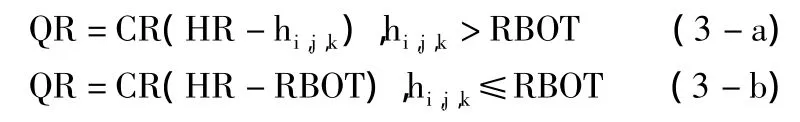
式中:QR为河流与含水层之间的流量，水流由河流流向含水层时取正值;HR为河流的水位;RBOT为河床基底处高程;hi，j，k为计算单元的水头值;CR为河流－含水层互相联接的水力传导系数(由河流长度、宽度、河床底积物厚度、河床底积物渗透系数计算得出)。由式3－a、3－b可以看出，该函数和排水沟与含水层间流量的函数相似，不同之处在于，河流不但能反映出周边地下水向管道中汇流的特征，亦能反映出管道内水流向周边含水层的补给。

4)溪流子模块(STR)

在Modflow中，溪流子模块的作用是计算溪流中的总流量和模拟地表水体和地下水的相互作用。溪流子模块计算地表水和地下水交换过程的函数与河流子模块并无二处。不同的是，在设置溪流时，溪流被分成节和段，每一段对应于单个的单元网格，而节是由以顺流顺序连接在一起的一组网格单元组成，通过指定每一节中第一段的溪流流入量来计算溪流流量，计算每段中邻近下游溪流段的流量等于上游溪流段流入量加上(减去)上游溪流段含水层流入(流出)的渗流量。相比于河流子模块，溪流子模块在输入时要求输入溪流流量，这就对岩溶管道模拟时添加了一个控制条件，模拟时不但减少了模型的校正过程，同时也提高了模拟精度。

2 模块实际应用效果检验

以一简易理想模型对各模块实际应用效果进行验证说明。该验证模型范围为一长3 000m，宽2 000m的区域，在X=800处为地表分水岭，分水岭右侧Y=果行验证处为一由西向东发育的岩溶管道，模型右侧为一高程为200的河流排泄基准面，同时在模型X=2000，Y=1000处设置一地下水位观测点，以检验暗河水位的动态变化。模型运行时间为一年，假定其气候类型为北半球亚热带季风气候，即夏季多雨冬季少雨。

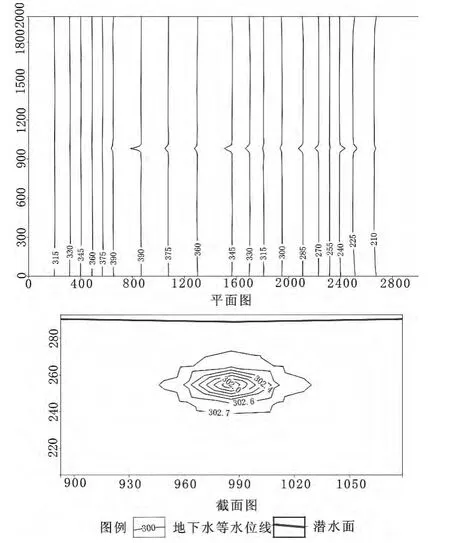
图2 单元渗流计算子模块模拟水位等值线

使用单元计算子模块概化模拟岩溶管道的模拟结果(见图2)可以看出，通过为岩溶管道区域赋上折算的水文地质参数后，模型反应出了岩溶管道周围地下水的运动规律:在管道发育区域，管道周围地下水水头较水流通畅的管道内的水头高，表现出管道围岩的地下水向管道中汇集。一般说来，大型的岩溶管道往往是岩溶地下水的控水介质，它控制着岩溶水的运动，并使之成为具独特形状的地下水位曲面[4]，但这一特性在模型中并未表现。同时，从监测钻孔的水位动态变化(见图6)也可以看出，模型中暗河水位也没有呈现出现实中随干枯两季大幅变化的性质，且模型中暗河水位的变化与大气降雨也呈现出明显的滞后性。这是因为使用折算含水参数概化岩溶管道时，并没有改变其为孔隙含水介质的本质，这种方法可以简单的模拟岩溶管道的储水和输水功能，但不能有效的模拟岩溶管道的控水功能。同时，此方法的前提条件是溶蚀管道处于饱水带中，对于补给源自地表水的伏流型管道并不能进行模拟。因此，这种运用折算参数模拟岩溶管道的方法只适用于埋深大、环境相对封闭、处于饱水状态的岩溶管道，此时管道主要起到储水和输水的作用，而不适用于模拟埋深浅、动态变化大、处于包气带或季节交替带的岩溶管道。

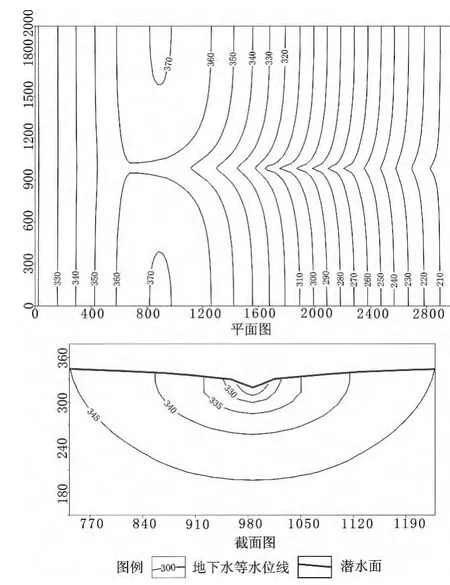
图3 排水沟子模块模拟水位等值线

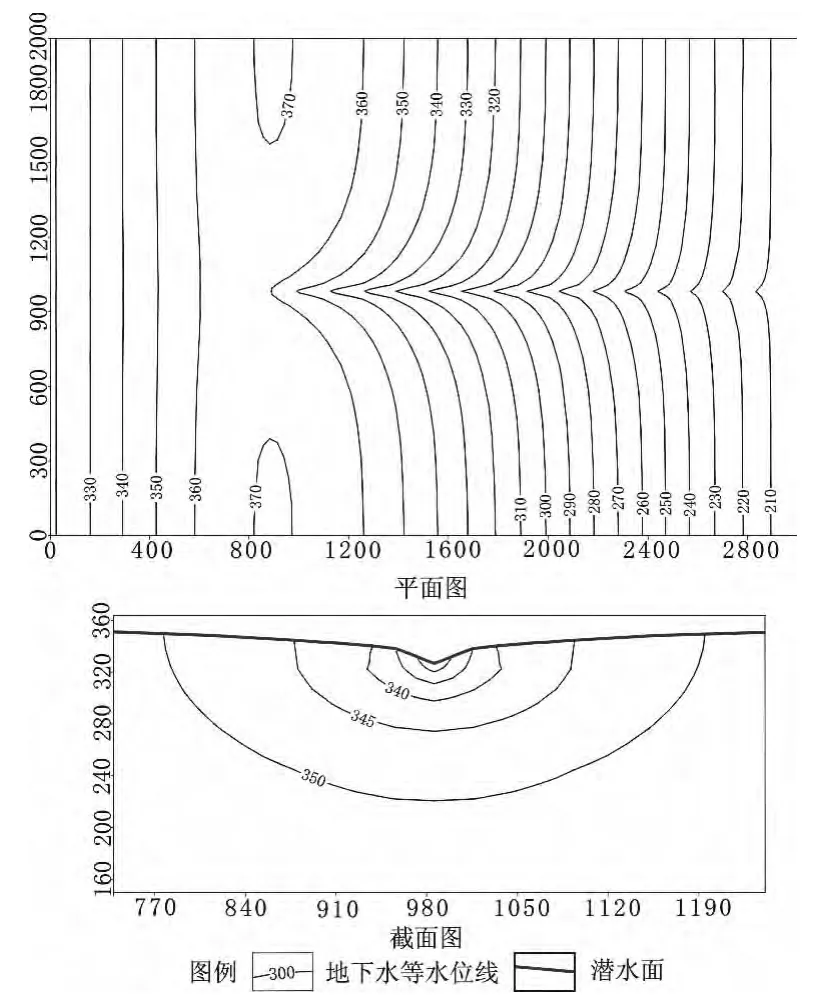
图4 河流子模块模拟水位等值线

如图3所示，使用排水沟子模块模拟岩溶管道可以很好的反应出岩溶管道介质的控水作用:管道两侧地下水向管道汇集，地下水位形成一定的漏斗形态。同时，监测钻孔显示的模型中暗河水位的动态特征也符合自然状态中暗河水量随干枯两季的起伏变化。但是，如果岩溶管道发育于包气带，管道中的地下水补给源自地表水时，模拟中排水沟水头高于含水层水头时，排水沟并不会像天然状态下那样表现出暗河管道内的水对地下水的补给。因此，通过适当的赋值将排水沟子模块用于模拟常年处于周边地下水位以下的、开放式的岩溶管道是合适的，但并不适用于处于地下水位以上的伏流型岩溶管道的模拟。

如图4所示，河流子模块在模拟岩溶管道时体现出了岩溶管道在开放系统中的控水作用，同时也能模拟出管道内地下水和含水介质中地下水的相互交换。监测钻孔也显示(图6)，模型中钻孔水位随干枯两季剧烈变化。因此，河流子模块能很好的用于模拟各类大型岩溶管道。由公式(3)知，在缺乏全面的地质资料时，使用河流－含水层互相连接的水力传导系数(CR)来表示一个三维流过程是一种经验做法，在模型调试时需要经过进行大量的校正。

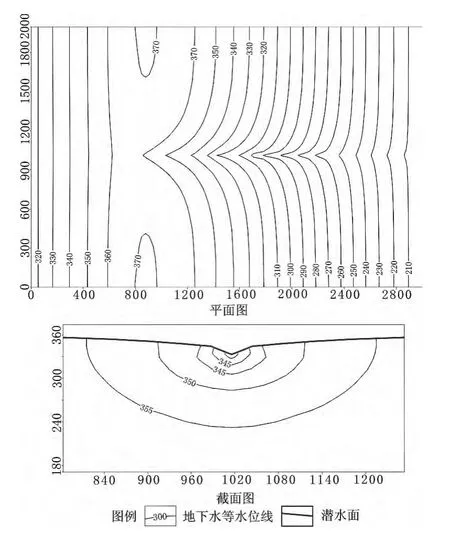
图5 溪流子模块模拟水位等值线

图6 不同模块模拟下监测钻孔水位动态变化特征

使用溪流子模块概化岩溶管道的模拟结果(图5)同河流子模块模拟的结果十分相似。溪流子模块不但模拟出了岩溶管道应有的特性，同时，有了流入端流量数据的控制，溪流在模拟有伏流入口的岩溶管道时更加精准。

表1 各子模块模拟岩溶管道适宜性对比

3 结论

管道－非管道介质的地下水流动模拟问题是地下水流动模拟领域难度最大的问题。笔者在现今已十分成熟的等效连续多孔介质模型的基础之上，将复杂抽象的管道条件用相对具体且成熟的模型模块进行概化，同时保证其在水力联系方面的统一性。通过模型实践证明，在Modflow中使用河流子模块和溪流子模块概化能最好地模拟岩溶管道周边地下水的流动和动态变化;此二者在实践中需要较多参数的支持以及较多的模型矫正。这种概化岩溶管道的方法在保证岩溶区地下水渗流场较为精确模拟的前提下，大大简化了模型的模拟概化过程，为实际应用提供一种思路与可能。由于岩溶含水介质自身的特殊性和复杂性，该方法在实际应用过程中仍待改进。

[1]刘国，毛邦燕，许模等.复杂岩溶含水介质概化初探[J].物探化探计算技术，2007，29(5):439 －442.

[2]Georgios Panagopoulos.Application of MODFLOW for simulating groundwater flow in the Trifilia karst aquifer，Greece[J].Environ Earth Sci，2012，67(7):1877 －1889.

[3]毛邦燕.复杂岩溶介质矿井涌水量的三维数值模拟研究[D].四川成都:成都理工大学，2005.

[4]陈雨孙，边际.岩溶水的介质和运动[J].中国岩溶，1988，7(3):229 －234.

[5]Michael G.McDonald，Arlen W.Harbaugh.A modular three－dimensional finite－difference ground－water flow model:U.S.Geological Survey Techniques of Water－ Resources Investigations[M].Washington:UNITED STATES GOVERNMENT PRINTING OFFICE，1988.

[6]陈崇希.岩溶管道－裂隙－孔隙三重空隙介质地下水模型及模拟方法研究[J].地球科学，1995，20(4):361 －366.

[7]陈崇希，胡立堂.渗流－管流耦合模型及其应用综述[J].水文地质工程地质，2008，35(3):70 －75.

[8]陈建梅，陈崇希.广西北山岩溶管道－裂隙－孔隙地下水数值模拟初探[J].水文地质与工程地质，1998，25(4):50－54.

[9]John J.Quinn，David Tomasko，James A.Kuiper.Modeling complex flow in a karst aquifer[J].Sedimentary Geology.2006，184(3):343 －353.