加里宁法分割地下水在熊岳站的应用

杨大卓

(辽宁省水文水资源勘测局营口分局，辽宁营口115003)

1 原理

在一般情况下山丘区的河流由地表水和地下水所补给径流而河流并不补给地下水，地下水补给河流的水量与降水渗入含水层的量及含水层的储水能力有关，流域含水层的最大储水能力是有一定限度的，地下水消退服从退水的指数衰减规律，即满足退水曲线方程:

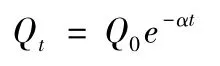
式中Q0为退水段起算时刻t0的流量;

Qt为时刻t的地下水流量;

α为地下水消退常数;

e为指数对数的底。

由上式积分便可得到以下地下水储量:

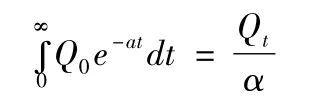
当 t=t0时，W0=Q0/α

加里宁试算法分割地下水是利用水量平衡法求得河流的地下水补给量，假定条件是含水层的来水量是与地表径流之间存在着比例关系，其比值函数等于河流地下径流与地表径流之比，所采用的来水量平衡方程可以近似地写成如下形式:

式中 W0、W1为时段初与末的地下水储量;

Ys为地表径流;Yg为地下径流;

B为比例系数，年地下径流与地表径流之比值。从以上公式中可以推导出地下径流量的通式为:

时段平均地下径流量为:

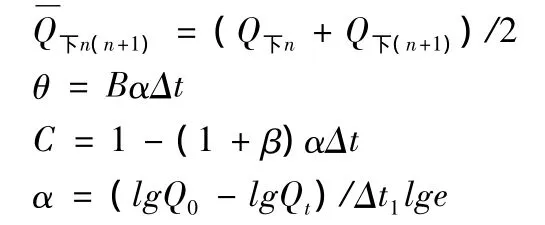
式中 Δt为计算时段长;

Δt1为Qt与Q0的时间差。

2 实例

熊岳河熊岳水文站积水面积307 km2，多年平均降水量704 mm，熊岳站以上未兴建大型水利工程，植被覆盖良好，以1995年熊岳站典型年流量资料为例分割地下水。

点绘熊岳站1995年逐日平均流量过程线，在过程线上选择退水规率较好的不受降水影响的曲线下部一段，推求其退水常数 α =0.042。

计算时段Δt的选用和统计河川径流的平均值Q河，选用计算时段Δt=10日，然后统计时段河川径流极其平均值。

B值的试算及第一个时段Q地下，如果算出的Q地下均不大于相应时段Q河值，则认为B值选用是合理的，否则为不合理，应另设B值重新进行试算，直至合理为止。B=0.05，第一个地下流量假定为0.30m3，K=W地下/W地表=0.052，计算成果及水位过程线分别如表1。

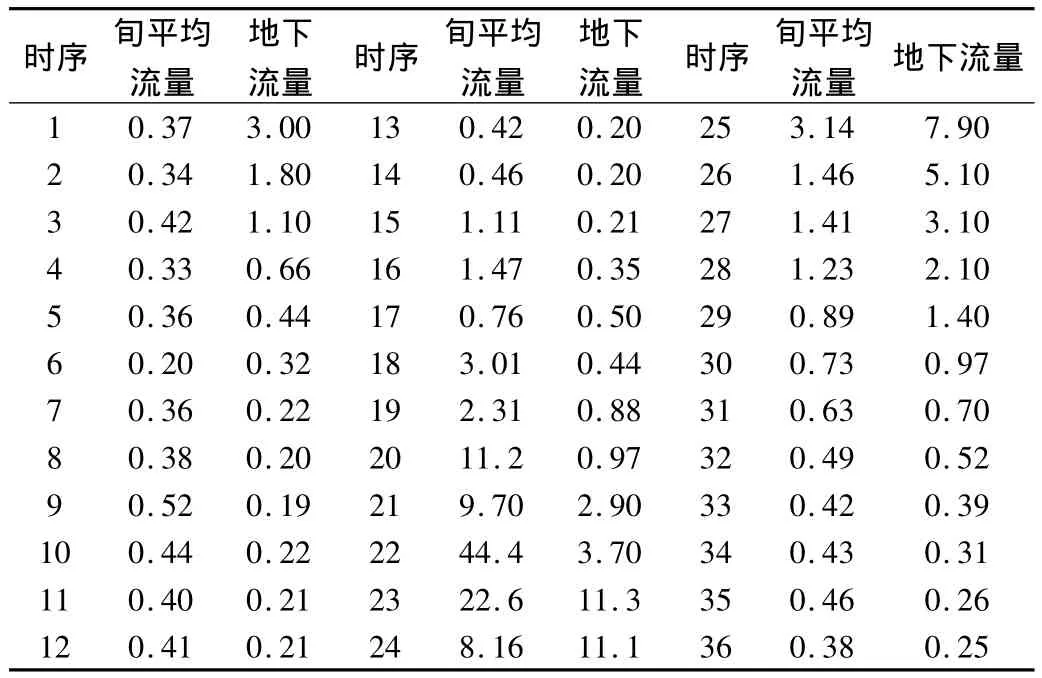
表1 1995年熊岳站地下流量计算表 单位:m3

3 结语

用加里宁试算法分割地下水具有一定的理论基础，计算方法固定，其成果不会因人而异。值对成果影响较小，采用系列中的典型年资料估算地下水资源其成果与长系列资料所求的结果比较接近，计算成果较好。特点是工作量大，计算比较繁琐，如采用计算机计算便可以节省许多工作量。