唐山某厂区地下水开采对区域地下水位影响预测研究

梅 凯

(河北省煜环环保科技有限公司，河北石家庄050000)

1 研究区水文地质条件

1.1 含水层(带)的空间分布及其水文地质特征

根据水文地质调查，按照地下水的赋存条件、水理性质及水力特征，将研究区地下水划分为第四系松散岩类孔隙水和奥陶系石灰岩溶裂隙水。两含水岩组无稳定的隔水层，水力联系密切，具有统一的水位，同时具有潜水特征，可视为同一地下水系统。

1)第四系松散岩类孔隙水。松散岩类孔隙水含水岩组，岩性主要为第四系上更新统的粉土、粗、中砂，底板埋深约50～100m，地下水的主要补给方式为大气降水入渗、地表水下渗补给及侧向径流补给，主要排泄方式为向下越流、侧向径流。地下水径流方向基本与地形坡向一致，总体径流方向自西向东。

2)岩溶裂隙水。岩溶裂隙水含水岩组，分布于场地及其周围的地面以下的奥陶系石灰岩岩溶裂隙中，单位涌水量100～250m3/h·m，地下水的主要补给方式为上覆第四系孔隙水入渗越流补给及侧向径流，主要排泄方式为人工开采。

1.2 包气带岩性及其空间分布特征

评价区的包气带岩性主要为第四系松散岩类，包气带厚度变化较大，松散岩类分布区包气带厚度般为小于40m。从地表看包气带岩性，第四系松散岩类分布于评价区大部分区域，主要岩性为粉土，其次为河道附近的细砂。

1.3 地下水的补给、径流、排泄条件及其动态变化规律

1)地下水的补给、径流、排泄条件。区内地下水的补给来源主要为大气降水入渗补给与侧向径流补给。松散岩类孔隙水:主要补给来源有两种;其一是来自同一水文地质单元的上游水平方向地下水径流补给及侧向径流补给;其二是地表水入渗补给。岩溶裂隙水:主要补给来源有两种;其一是来自同一水文地质单元的上游水平方向地下水径流补给及不同水文地质单元的侧向补给;其二是松散岩类孔隙水的垂直渗入补给。两种类型地下水在不同地段相互补给，具有统一的地下水位，联系密切。

地下水径流方向基本与地形坡向一致，评价范围的内径流方向是由西向东，水力坡度一般为5‰～25‰。且呈现从上游至下游水力坡度度逐渐减缓的趋势。

排泄方式主要为工业开采利用，其次为向下越流、侧向径流及潜水蒸发。本区各类型地下水迳流距离短，具有就近补给、当地排泄的特点。

2)地下水水位动态特征。本区地下水位动态变化与补径排条件密切相关，其年变化过程大致可分为开采下降、补给回升及相对稳定三个阶段。

水位下降期:地下水位下降主要受开采影响。历年的4－5月份降水量比较少，又是农业春灌集中开采期，加之河道径流量较小，造成水位缓慢下降，至5月底出现最低水位。水位下降幅度在1～3m以内。

水位回升期:6月份雨季来临，河道径流量增加，河道渗漏补给和大气降水入渗补给明显增多，加之农灌停采，区域地下水位普遍回升，回升幅度1～3m，至9月底出现最高水位。

水位稳定期:进入10月份，受农业季节性开采影响，水位又转为缓慢下降阶段，持续到11月初，12月初至次年2月，地下水位进入相对平稳阶段，水位升降变化幅度一般小于1m。

研究区地下水动态特征为降水入渗补给——开采排泄型，本类型地下水受大气降水垂直渗透补给和开采消耗影响明显，水交替作用强烈，水位升降幅度较大，尤其是近年来随着区域工业发展和新民居小区的建设，地下水开采量影响地下水动态变化特征越来越明显。

地下水动态变化规律是:主要随大气降水补给量而发生变化，同时区域地下水开采量又决定地下水水位变化幅度。通过本次研究发现，研究区内除了工业用水外，大部分为乡镇居住小区和村庄生活用水，农业用水极少。随着降雨量的变化，在6月份以后大气降雨量骤然增大，但由于天气变暖工业及生活开采量增加，地下水位并未上升速度变缓，最高水位与最低水位变幅差值一般低于3m。

1.4 主要开采含水层(带)与其它含水层、地表水体之间的水力联系

由前面的论述可知，松散岩类孔隙水与岩溶裂隙水是评价区的两个主要的地下水类型，两类地下水之间没有稳定的隔水层，水力联系密切，并且地下水位埋藏较深，决定了这两类地下水成为本区的主要开采层。

本区的地表水体是评价区中部和南部的沙河，调查期间该河流有少量的地表径流。从地下水位等值线图可以看出，沙河水位高于地下水位，河流渗漏补给地下水。

2 地下水数值模拟

采用地下水数值法进行地下水资源评价首先建立地下水系统的概念模型。在建立地下水系统概念模型的基础上再建立地下水流动模型。

2.1 水文地质概念模型

水文地质概念模型是地下水系统的一种近似的形象化表示，其目的是为了简化野外实际问题，便于对该地下水系统进行分析，建立数学模型，组织有关数据。水文地质概念模型的概化主要包括计算范围和边界条件的概化，含水层结构和水文地质特征的概化等[1]。

1)计算区范围。根据评价区水文地质条件特点，结合现有各类资料确定研究区模拟范围如下:模型北部边界是以山区与平原衔接处，作为弱透水的流量边界;南部边界为沙河，定为River边界;西部以唐家庄——林东一线的地下水分水岭为界，从历年地下水流场图上看，此处等水位线的形状变化不大，一直为地下水分水岭位置，因此西部边界可作为零流量边界处理;东部边界参照评价区多年平均的流场图定为通用水头边界;模拟区总面积约90 km2，如图1所示。

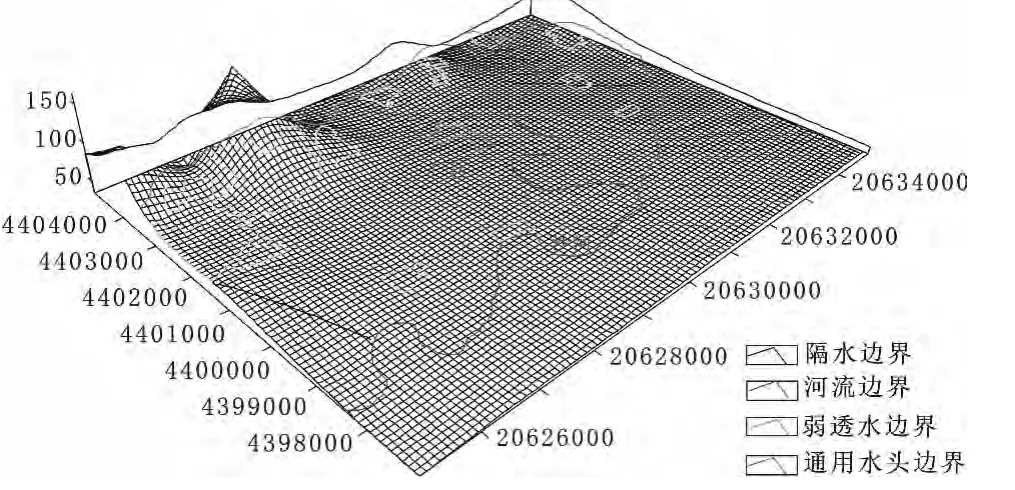
图1 模拟计算区范围示意图

2)含水层的概化。松散岩类孔隙水与岩溶裂隙水是评价区的两个主要的地下水类型，两类地下水之间没有稳定的隔水层，水力联系密切，可以将水流模型概化为一层，作为非均质各向同性潜水二维平面流处理。实际上对于区域水流来讲，垂向上水力联系比较密切，多年地下水动态资料也没有分层检测，在垂向上没有水压力分布资料验证模型，只能暂时将各层的水力特征认为是一样的(表现为等效的水力特征，具有同样的水文地质参数，统一的地下水流场)。

2.2 地下水流数学模型

综上所述，将评价区的地下水流系统概化为非均质，各向同性，二维非稳定流的地下水流系统。其数学模型为[2]:

式中:Ω－渗流区域;

H－地下水水位标高(m);

K－含水层在水平方向上的渗透系数(m/d);

ε－含水层的源汇项(m/d);

H0－初始流场(m);

Γ2—渗流区域的二类边界;

n－边界面的法线方向;

q－Γ2边界上的单宽流量(m2/d)，流入为正，流出为负;

Z(x，y)—含水层底板高程。

2.3 地下水流数值模型的建立

1)区域剖分。对整个区域模型采用矩形网格剖分，剖分为80行100列，边长为0.1 km×0.1 km，共剖分矩形网格单元8000个，其中有效单元4664个，计算节点位于单元中心。模拟区网格剖分见图2。

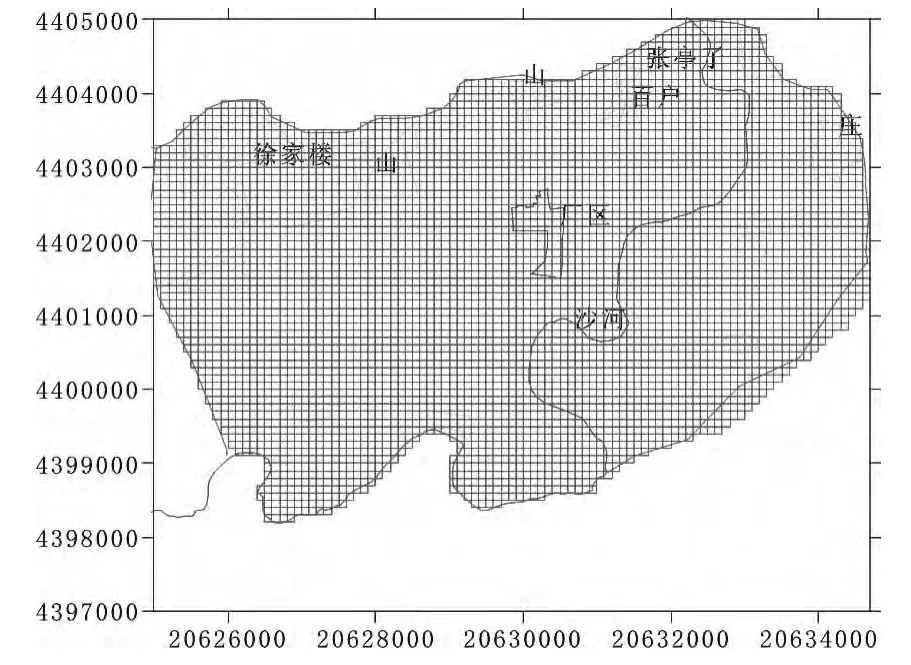
图2 模拟区网格剖分图

2)源汇项处理。

(1)大气降水入渗补给量。潜水含水层通过包气带接受大气降水入渗补给。降水入渗补给条件的不均匀性用入渗分区概化处理。依据有关降水入渗资料，并参考包气带岩性、潜水位埋深、地形、植被等因素，绘出全区降水入渗系数分区图，分别给出各区降水入渗系数平均值，加在模型对应的剖分网格单元上。根据各区面积、降水量、降水入渗系数来计算降水入渗补给量。

当降水量较小时，难以补给地下水，所以当月降水量小于10 mm时，不计入有效降水量。

(2)地下水开采量。研究区内潜水主要是用于居民生活用水和企业用水。

研究区内地下水开采有集中开采、农村生活用水分散开采。集中开采为卑家店水厂供水水源地和各个企业自备井开采，其开采量按实际调查的开采量加在水源地对应的网格节点上。农村生活用水分散开采，按开采强度进行分区概化，分别给出各区开采强度，加在模型对应的剖分网格单元上。

(3)蒸发。潜水蒸发是指潜水(埋深小于4米时)在毛细管力的作用下向上运动，最终以参加陆面蒸散发形式散逸到大气中的水分损失量。评价期内潜水埋深均超过了4米，潜水蒸发量按零计[3]。

(4)河流入渗[4]。模型中将沙河作为第三类边界条件——混合边界(River)处理。从河流横剖面示意图(图3)上看出，河流通过低渗透性底积物与含水层发生水力联系，根据达西定律，横剖面法线上河流和含水层的交换量示，所以整个河流和含水层的交换量可用公式(1)表示(图4):

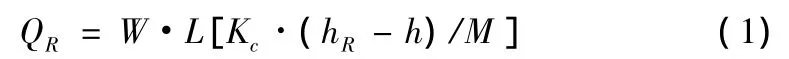
式中:QR为河流侧渗量;

hR为河流水位(m);

h为地下水位(m);

W为河流宽度(m);

M为河床底积层厚度(m);

KC为河床底积层厚度渗透系数m/d;

L为河流长度。

因此，河流和含水层之间的交换量由河水水位hR、潜水水位h、底积物的渗透系数Kc、底积物的厚度M以及河流的长度L宽度M共同控制。把各段水位和参数写入Modflow中的River程序包，便可计算沙河渗漏补给。

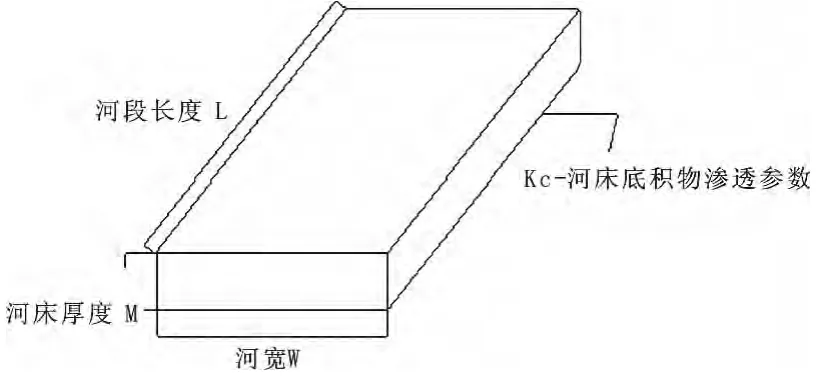
图3 河流横剖面示意图

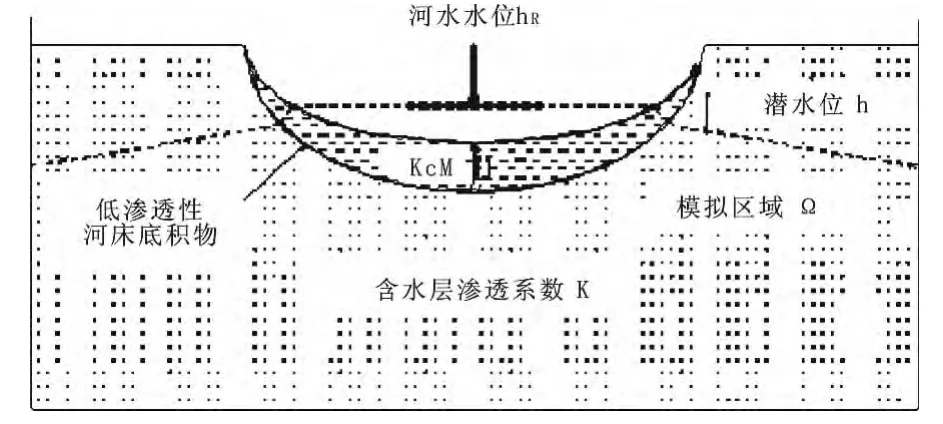
图4 河床水力传导的理想化模型示意图

3)初始条件设置及模拟识别

根据所掌握的资料，本次模拟识别期选为2012年9月1日到2013年3月1日，应力期以月为单位，共划分为6个应力期，每个应力期又包括若干个时间步长，时间步长为模型自动控制，严格控制每次的迭代误差，在同一应力期内地下水补排项不变。

4)模拟识别

模型的识别过程是整个模拟中极为重要的一步工作，通常要在反复修改参数和调整某些源汇项基础上才能达到较为理想的拟合结果。此模型的识别过程采用的方法称为试估—校正法，属于反求参数的间接方法之一。

为了确保模型求解的唯一性，在模型调试过程中充分利用各种定解条件，也就是用那些靠得住的实测资料来约束模型对原形的拟合。在模型调试过程中，还充分利用水文地质调查中获得的有关信息及计算者对水文地质条件的认识，来约束模型的调试和识别。

本次模拟首先进行了稳定流计算，以便拟合潜水的初始流场(见图5)，这样做避免了直接建立非稳定模型多参数识别的不便，通过建立相对于非稳定流模型输入输出简单的稳定流模型，运用了模型反求参的方法获得含水层渗透系数。另外，概化的含水层的结构也在建立稳定流模型时确定下来，直接运用于非稳定流模型。这样非稳定流模型的参数识别过程就可以只确定给水度的大小，因此增加了此次模型的可信性[5]。

接着用稳定流拟合的潜水的初始流场(2012年9月1日流场)作为非稳定流模拟的初始值(和实测的初始等水位线比起来，稳定流模拟计算得出的流场能更明显地表现出评价区的水文地质条件)，运行计算程序，通过拟合同时期的流场，识别水文地质参数、边界值和其它均衡项，使建立的模型更加符合模拟区的水文地质条件。

模型的识别和验证主要遵循以下原则:(1)模拟的地下水流场要与实际地下水流场基本一致，即要求地下水模拟等值线与实测地下水位等值线形状相似;(2)从均衡的角度出发，模拟的地下水均衡变化与实际要基本相符;(3)识别的水文地质参数要符合实际水文地质条件。根据以上三个原则，对模拟区地下水系统进行了识别和验证。通过反复模拟、识别后的水文地质参数较好的刻划了地下水系统的水文地质特征，基本反映了地下水随时间和空间的变化规律，使水位拟合误差较小，达到预期效果。验证后的平面流场和优化调整后确定的参数分区分别见图6至图8，分区参数值见表1和2。

图5 2012年9月1日潜水等水位线拟合图(初始流场拟合)

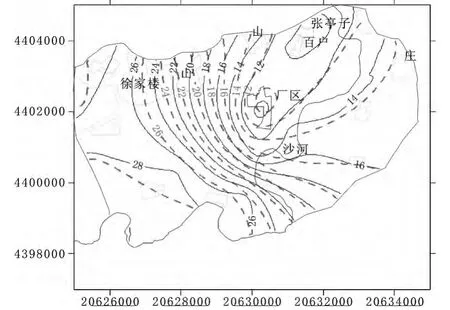
图6 2013年3月1日浅层水等水位线拟合图(验证)

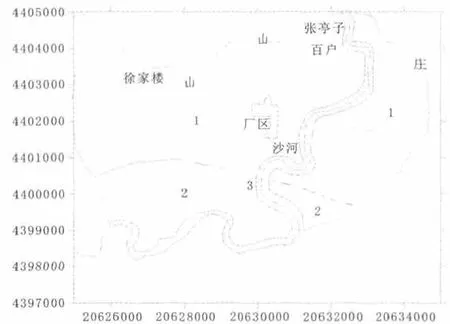
图7 包气带降水入渗系数分区图

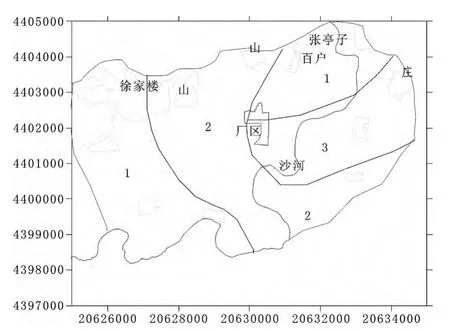
图8 含水层参数分区图

表1 潜水含水层水文地质参数分区表

表2 降水入渗系数参数分区表

3 厂区取水对地下水水位的影响预测

厂区新鲜供水拟由位于厂区东北的卑家店水厂水源井(卑家店水厂水源井位于后巍峰山东与沙河之间)来供给，新增开采量规模为1 235m3/d。

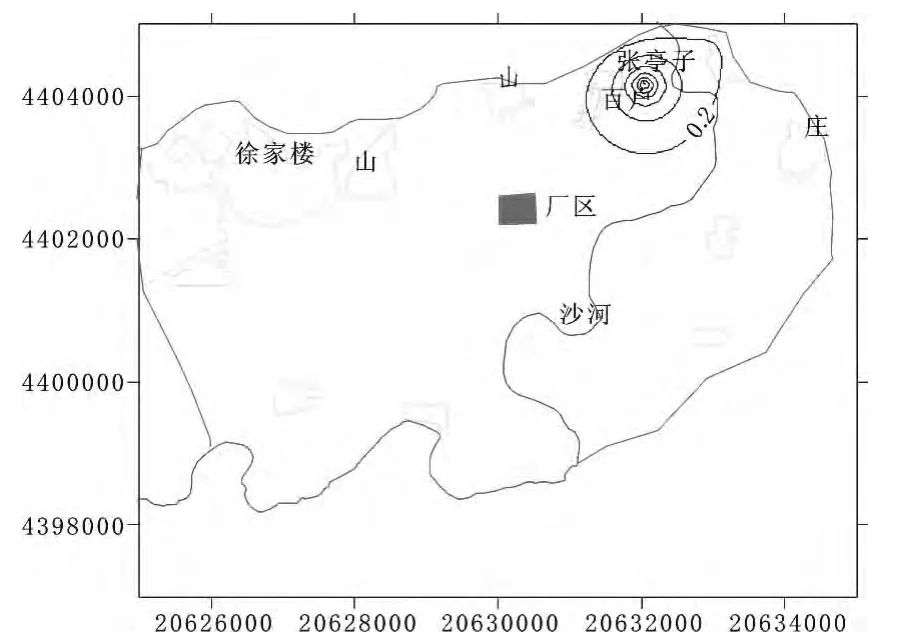
图9 开采1年后等降深预测图

为了预测该项目增采地下水对水源地附近区域流场的影响，利用上述识别和验证的模型按照既定开采方案，分别对水源地连续增采20年后的地下水等降深场进行了预测。结果表明:增采1年后水源地漏斗中心降深达1.32米，3年后水源地漏斗中心降深达1.43米，5年后水源地漏斗中心降深达1.46米，且基本达到稳定，其降深等值线图分别见图9至11。由水源地漏斗中心降深历时曲线(图12)与降深等值线图(图9至11)分析可知，增采所引起的区域水位下降并不大，扩展范围相对比较小。但是鉴于研究区目前由于多个大型企业以及居民生活用水对地下水的开采，已经造成了该区域地下水位的明显下降，含水系统遭到了一定的破坏，使得该区域的地下水资源量正在逐步减少，因此建议政府水务行政职能部门严格规范控制该地区各行各业的地下水开采量，开展一水多用，开源节流等节水措施，并逐步减少对地下水开采，维护地下水采补平衡，同时建议进一步加大外来水的供应，减小水资源供需矛盾。

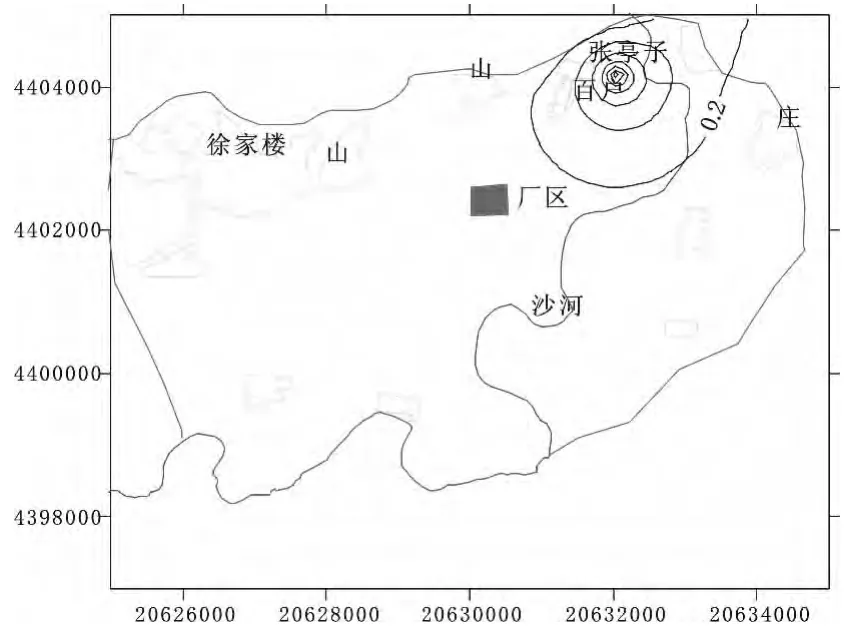
图10 开采3年后等降深预测图

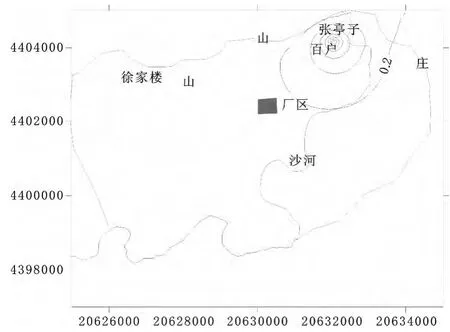
图11 开采5年后等降深预测图

图12 水源地漏斗中心降深历时曲线

4 结语

利用通用的地下水模型软件 Visual Modflow建立了研究区的地下水流模拟模型。此次数值模拟过程，笔者首先建立了稳定流模型，然后以此为基础建立非稳定流模型，这在建立地下水模型时避免了直接建立非稳定模型多参数识别(渗透系数、给水度和储水系数一起识别)的不便。建立的地下水非稳定流模型可以有效预测地下水动态，从而对该厂区开采地下水进行了可靠的预测评价。

[1]薛禹群，李同斌，贾贵庭.地下水动力学[M].北京:地质出版社，1997.

[2]王旭升，万力.地下水运动方程[M].北京:地质出版社，2009.

[3]迟宝明，王文科，宫辉力，等.专门水文地质学[M].北京:地质出版社，2009.

[4]郭卫星，卢国平.模块化三维有限差分地下水流动模型[M].南京:南京大学出版社，1999:111－113

[5]朱奎.大区域地下水数值模拟[D].武汉:武汉大学，2004:46－47