用记忆型BP神经网络实现HPA预失真的算法研究

黄春晖，温永杰

(福州大学 物理与信息工程学院, 福建 福州 350108)

1 引言

随着现代无线移动通信技术的发展，CMMB直放站作为局域网环境下用来延长网络距离和提高信号质量的最简单最廉价的互联设备，得到广泛的应用。CMMB直放站传输信号存在对噪声敏感和峰—均功率比(PAPR，peak to average power ratio)较大等缺点。因为CMMB信号经常使HPA工作在饱和区，由此产生幅度失真(AM-AM)和相位失真(AM-PM)，造成邻道干扰(adjacent channel interference)和带内失真，导致系统性能下降。所以，需要提高直放站系统HPA的线性放大特征。

目前，普遍认为自适应数字预失真是一种较有前途的HPA线性化方法。虽然数字预失真技术有多种多样，但大致分为3类：1）基于查找表（LUT）的预失真器，算法简单但是算法收敛速度较慢[1,2]；2）基于Volterra级数预失真器，收敛较快但存在着所需乘法数随着阶数增加而呈现非线性增加，导致计算量大等不足[3~5]；3）由神经网络构成的预失真器，利用BP神经网络（BPNN）的学习可以逼近任意非线性函数，能很好地拟合 HPA的 AM/AM、AM/PM特性。此外，延时的BPNN还能同时拟合HPA的非线性和记忆效应[6~10]。

用实数延时神经网络（RVTDNN）模型构建的带记忆HPA数字预失真器，具有很好的性能，但是该模型也存在着参量多、计算量大等缺点[10,11]。为了减少参量数目，提高计算速度，本文提出了一种新的BP神经网络预失真器模型，简称FIR- NLNNN。该模型把Bayesian和LM算法有机地结合，运用到网络训练优化中，有效地消除LM算法的过拟合现象。仿真结果表明RVTDNN和FIR-NLNNN 2种结构的预失真器均能提高系统线性特性，降低系统邻信道功率比30 dB。在不降低系统线性化性能的前提下，FIR-NLNNN比RVTDNN结构更简单、计算量更小且随着网络输入抽头的增加，网络的参数和训练算法计算量基本不变。

2 功放模型及BP神经网络结构

2.1 功放模型

在HPA的预失真过程中，AM/AM和AM/PM特性越接近HPA的行为模型，说明数字HPA预失真器越好。典型的功放模型有Rapp模型、Ghorbani模型、Volterra级数模型和Saleh模型[12]。其中，Saleh模型具有结构简单、计算量小且能够精确拟合HPA幅度和相位特性。如果Saleh的参数选择得当，也能很好地拟合实际功放的非线性和记忆效应[13]。因此本文选用 Saleh模型作为 HPA的行为模型。其AM/AM和AM/PM特性表达为

其中，r为输入信号的幅度，由式(1)可知，功放的幅度和相位失真只与输入信号的幅度有关。参数αa、βa共同决定幅度的非线性失真程度。参数αp、βp决定相位偏移程度。由于 CMMB信号属于宽带信号，当对这种信号进行放大时，功放的记忆效应不可忽略。为此，本文采用在Saleh功放模型之后级联一个FIR滤波器作为带记忆效应的功放模型，它属于Hammerstein系统模型[14]。

2.2 BP神经网络结构

多层感知神经网络（MLBPNN）是数字通信中最常用的神经网络结构。MLBPNN由一个输入层、中间隐藏层和一个输出层组成的全连接型结构。其中隐藏层和输出层由若干个神经元组成，网络中的每个神经元由线性混合器和激活函数两部分组成，可表达如下[15]

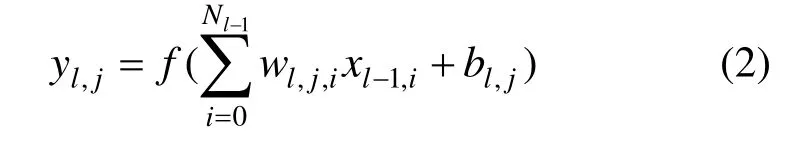
其中，yl,j表示第i层中第j个神经元的输出，wl,j,i表示第i层中第j个神经元与第i-1层中第i个神经元的连接权系数，该神经元的第 i个输入为xl-1,i，偏置值为bl,j，Ni为第i层的节点或神经元个数。本文选用作为隐藏层神经元的激活函数， xxf =)( 作为输出层神经元激活函数。

3 预失真延时神经网络模型的构建

当输入信号平均功率较大时，HPA工作在饱和区，HPA的热效应和记忆效应不可忽略，此时输出即与当前的输入有关又与过去的输入相关[16]。需要用延时型神经网络才能实现记忆型功放的预失真性能。为了能够分离处理HPA的非线性和记忆效应，本文提出一种新的延时 BP神经网络结构。

3.1 构建新的延时神经网络预失真器

本文提出一种能分离处理 HPA的非线性和记忆效应的神经网络 FIR-NLNNN，其基本思想是：假设HPA系统是由2个相对独立的子系统构成：无记忆的非线性部分(NLN)和带记忆的线性部分(FIR)，两者级联成为带记忆的非线性Hammerstein HPA，可以用一个Wiener系统来预失真[17]。实际上，FIR-NLNNN预失真系统就是一个由线性和非线性2个部分组成的Wiener预失真系统。其中线性部包括2个FIR滤波器，非线性部分是一个双入双出的3层普通MLBPNN。其结构如图1所示。该结构虽然只在MLBPNN结构的前面增加FIR功能，但它可以分离地处理Hammerstein HPA的功放的非线性和记忆效应。这样做可以简化网络规模减少网络参数，从而减少系数更新迭代的计算量。

图1 FIR-NLNNN结构

由式（2）可知，FIR-NLNNN前馈计算为

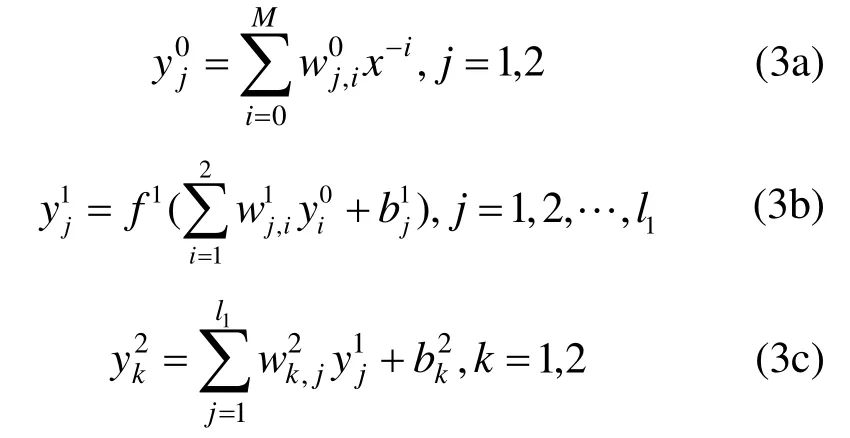
其中，M 为记忆深度，隐藏层激活函数 f1为 tanh函数，l1为隐藏层节点数。

图2是典型的RVTDNN模型[18~22]，比较图1与图2可以看出两者不同之处在于RVTDNN将输入经过抽头延时直接作为网络输入，而 FIRNLNNN先将输入进行FIR滤波再进入网络处理，使网络参数和计算量大大减小，详情将在3.3节予以介绍。

3.2 间接神经网络学习结构

在实际工作中，功放单元的参数具有随着温度、电器特性和应用环境变化的时变特性。这要求预失真器必须具有自适应地跟踪拟合功放参数的功能[23]。本文把FIR-NLNN模型用于神经网络学习结构以满足时变特性的要求，其结构如图 3所示。

图2 RVTDNN结构

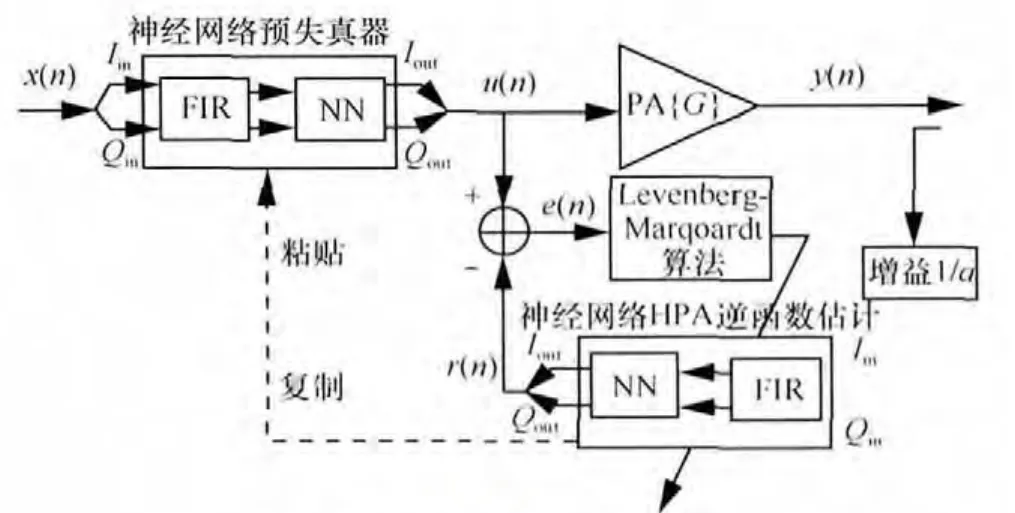
图3 间接神经网络学习结构

图4 中预失真器和估计函数结构相同，不同之处在于前者以前向信号x(n)为输入信号，后者以反馈信号为输入信号。预失真器PD的输出u(n)与估计函数的输出r (n)之差作为误差e(n)，通过神经网络系数迭代计算实现估计函数的系数更新，并将更新后的系数复制到预失真器PD中。当预失真器与级联的 HPA实现线性放大时，神经网络就等效于PA的反向传输函数。

4 优化算法的改进

与梯度下降法、共轭梯度算法和牛顿法等相比，LM 算法具有收敛速度较快、计算量适中等特点，因此本文采用LM算法作为神经网络系数的迭代更新算法[20,21]。文献[24]具体介绍了用LM算法更新RVTDNN网络系数的过程，本文侧重介绍LM算法中FIR-NLNNN网络系数的更新过程，并且在神经网络预失真系统中引入 Bayesian算法，通过把Bayesian和LM算法有机的结合，以消除LM算法的过拟合现象，称之为Bayesian-LM算法。

4.1 LM优化算法

如果网络目标函数V(x)为均方误差函数，即

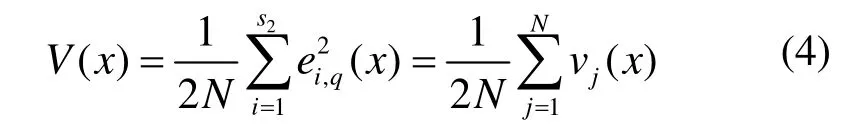
其中，q为每回合用于训练的样本数，s2为输出层节点数。那么()x∇V和2()Vx∇满足下列公式

其中，J为系数的Jacobi矩阵，包含误差权系数的一阶偏导信息，其计算量远小于 Hessian矩阵。为误差构成的误差向量。Jacobi矩阵J的表达式为

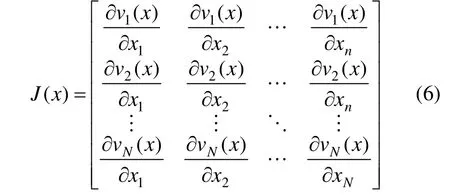
其中，由权系数构成的系数向量X为

式（6）中有关误差 e(n)对系数 W1和 W2的偏导可以通过改进的BP算法计算，计算过程详见文献[24]。在 FIR-NLNNN网络中，LM 算法新增加参数 W0及其误差 e(n)对它的偏导，具体推导如下。

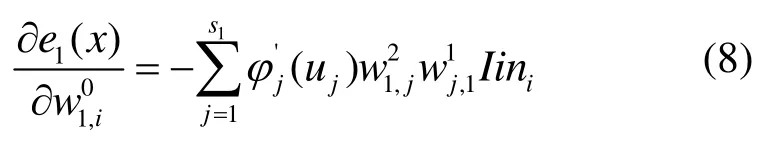
类似地可以推导得到其他分量表达式。

将式（8）代入式(6）中即可得到系数的Jacobi矩阵表达式，则神经网络的系数迭代公式为

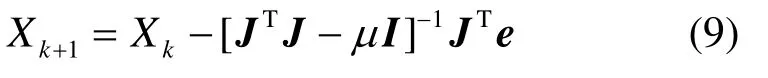
其中，I是单位矩阵，μ是算法的学习率。LM算法的一个显著的特点在于，当μ取较大值时，它接近于一阶收敛的梯度下降法。当μ取较小值时，它接近于二阶收敛的算法；当μ下降到0时，算法变成了高斯—牛顿算法。

4.2 Bayesian-LM优化

针对LM算法有可能造成HPA预失真神经网络的过拟合缺陷[25]，本文引入Bayesian正则化算法，修改网络的目标性能函数，可以消除LM算法的过拟合现象。即在目标函数式（4）中增加一项，此项为网络参数权值的平方和均值项，新的目标函数表达式为

其中，ED即式(4)中的V(X)，，其中，wj为网络权值。可见，通过新的目标函数，可以保证网络训练误差在尽可能小的情况下使网络具有较小的权值。根据公式计算推导可得Bayesian-LM更新神经网络系数的迭代公式为

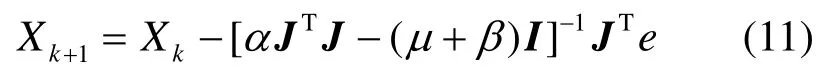
式（11）是Bayesian和LM算法的有机结合，其中，α和β通过Bayesian算法获得，网络的系数通过LM更新。

正则化的难点在于确定 α、β的最优化值，而Bayesian正则化算法可以在网络训练的过程中自适应的调整确定两者的最优化值。在Bayesian正则化算法中认为网络权值是随机变量，在获取数据之后，权系数的概率密度函数为

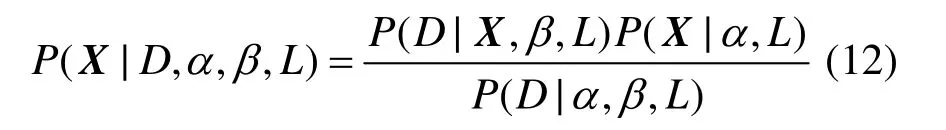
其中，D为网络数据集，L是所使用的神经网络模型，X为网络的权系数向量。P(X|α,L)是先验概率，表示在收集数据前对权系数值的认识。P(D|X,β,L)是似然函数，表示在取定权值矢量X情况下数据出现的概率。P(D|α,β,L)是归一化因子，保证总的概率为1。

利用式(12)可以获得 P(D|α,β,L)的解[25]为

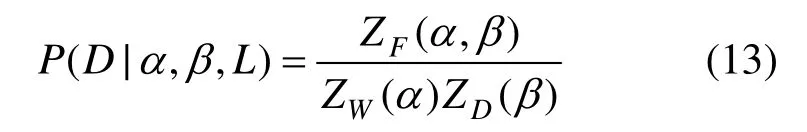
已知ZW(α)和ZD(β)为常数。由于目标函数在最小值点附近的领域内有二次型，因此可以在后验概率最小值点XMP附近泰勒展开目标函数。已知该点梯度为零，则可求解的归一化常数为

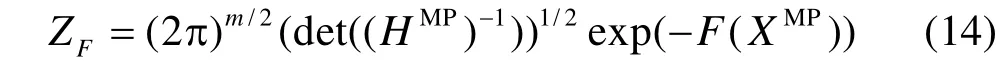
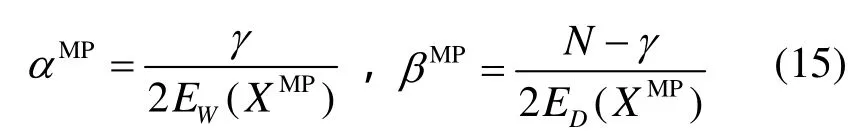
Bayesian-LM算法的操作步骤总结如下。

1) 初始化网络参数，并且初始化比例参数α=0，β=1。

5) 利用式（11）更新网络系数。

6）重复步骤2）~步骤4），直到算法收敛。

4.3 FIR-NLNNN和RVTDNN的比较

FIR-NLNNN和文献[21,22]所述 RVTDNN区别在于：RVTDNN将输入经过若干抽头延时作为神经网络的输入进而使神经网络能够拟合功放的记忆效应；而FIR-NLNNN是利用新增的FIR部分拟合功放的记忆效应，其网络结构更加简洁。以抽头延时为4、隐藏层的节点数为9为例，在RVTDNN中总的系数个数为119个。FIR-NLNNN结构虽然新增了10个新参数 W0，但总的系数个数只有 57个。这表明FIR-NLNNN结构更加紧凑，系数个数减少了近一半。

选择104个样本点用FIR-NLNNN和RVTDNN进行预失真，当MSE小于10-6时，两者所需的乘法、加法操作次数及执行时间如表1所示。结果表明，FIR-NLNNN的系数迭代过程所需的乘法操作、加法操作次数比RVTDNN结构少了近75%，执行时间少了近50%。

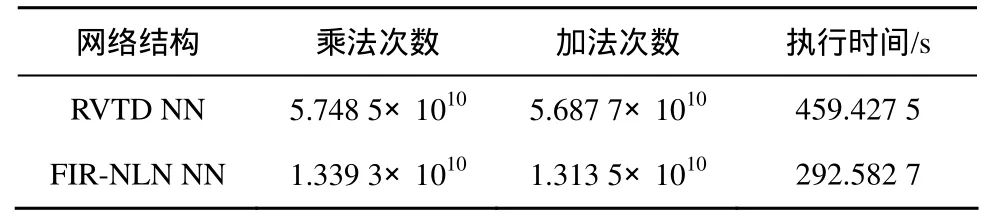
表1 LM算法的执行时间及迭代所需的浮点数操作次数

5 仿真结果的分析与讨论

采用图3所示的间接学习结构作为本文功放预失真系统。选Saleh模型作为带记忆功放模型，参数为，FIR的系统函数为，此时功放模型的增益1。输入信号为CMMB信号，取2种结构的抽头延时数同为 4，隐藏层节点数为 9，更新算法为 LM 算法，学习率取 0.8，优化算法为Bayesian算法。

预失真前带记忆功放的AM/AM和AM/PM特性如图4所示。由图4可知，AM/AM的特性是一条带迟滞的非线性曲线。当输入在0~1之间变化时，AM/PM 特性图上相位存在不同程度的偏移，输入越小时相位的偏移量越大。

图4 预失真前功放的AM/AM和AM/PM特性

功放预失真后的AM/AM和AM/PM特性图如图5所示。带预失真器的功放的AM/AM特性几乎为一条斜率为1的直线且不带迟滞，说明幅度放大基本上达到线性化。同时AM/PM特性在输入幅度变化时，输出相位的偏移基本为 0，说明相位预失真的目的基本上达到。这表明FIR-NLNNN预失真器和 RVTDNN预失真器均能有效地使 HPA线性化。

FIR-NLNNN和RVTDNN模型预失真器的均方误差（MSE）收敛曲线如图6所示。当迭代次数为10时，MSE均为10-6左右；当迭代次数为250时，MSE均为10-7左右，说明2种模型使用LM算法迭代更新时收敛速度快且性能相当好。当迭代次数为2 000次时，FIR-NLNNN预失真器的MSE收敛曲线如图 7所示，Bayesian-LM 算法很好地消除了LM算法在迭代1 380次附近出现的过拟合现象，保证了算法的持续收敛。

从图8的预失真前后功放的功率谱可见，预失真后带内信号变得平整，2种预失真器结构均能有效地降低30 dB左右的邻信道功率比。

图5 预失真后功放的AM/AM和AM/PM特性

图6 预失真器LM算法的均方误差曲线

图7 Bayesian-LM与LM算法的收敛曲线

图8 功放预失真前后功率谱

6 结束语

针对高功率功放的记忆效应和非线性失真，本文基于多层感知神经网络的预失真原理，在RVTDNN结构的基础上构建了一种新的预失真网络结构 FIR-NLNNN，该结构新增了网络参数W0，文中给出了误差e(x)对W0的偏导公式。在预失真神经网络中引入 Bayesian-LM 算法有效地消除LM算法的过拟合现象，保证算法持续收敛。通过 MATLAB仿真，结果表明，2种结构的预失真器均能较好地拟合功放的非线性和记忆效应，提高了系统的性能，使邻信道功率比降低 30 dB左右。与 RVTDNN结构相比，在保证相同的预失真器性能情况下，本文提出的FIR-NLNNN结构，可以将网络参数减少近50%，使网络结构更简单。在迭代优化过程中，乘法和加法操作次数减少近75%，说明FIR-NLNNN结构的计算量更少。

[1] CAVERS J K. Amplifier linearization using a digital predistorter with fast adaptation and low memory requirements[J]. IEEE Transactions on Vehicular Technology, 1990, 39(4):374-381.

[2] VARAJRAM P, MOHAMMSDY S, HAMIDON M N. Complex gain predistortion in WCDMA power amplifiers with memory effects[J].The International Arab Journal of Information Technology, 2010,7(3):333-339.

[3] MIRRI D, IUCULANO G, FILICORI F. A modified volterra series approach for nonlinear dynamic systems modeling[J]. IEEE Transactions on Circuits and Systems, Fundamental Theory and Applications, 2002,49(8):1118-1127.

[4] ZHU A, BRAZIL T J. Behavioral modeling of RF power amplifiers based on pruned voterra eries[J]. IEEE Microwave and Wireless Components Letters, 2004, 14(12):563-565.

[5] SAFARI N, ROSTE T, FEDORENKO P. An approximation of volterra series using delay envelopes, applied to digital predistortion of RF power amplifiers with memory effects[J]. IEEE Microwave and Wireless Components Letters, 2008, 18(2): 115-117.

[6] QIU W, ZHONG Z, REN G C. The research of adaptive digital predistortion based on SISO-neural network[A]. International Conference on Communications and Mobile Computing[C]. China, 2009. 451-454.

[7] ZAYNNI R, BOUALLENGUE R, ROVIRAS D. An adaptive neural network predistorter for nonstationary HPA in OFDM systems[A]. The 15th European Signal Processing Conference[C]. Poznan, Poland, 2007.1353-1354.

[8] DING Y M, JIAO D P, WANG J K. A review of adaptive predistortion techniques of HPA[A]. Asia Pacific Conference on Postgraduate Research in Microelectronics and Electronics[C]. Shanghai, China, 2009. 341-343.

[9] ZAYNNI R, BOUALLENGUE R. Predistortion for the compensation of HPA nonlinearity with neural networks: application to satellite communications[J]. International Journal of Computer Science and Network Security, 2007, 7(3):98-101.

[10] BOUMAIZA S, MKADEM F. Wideband RF power amplifier predistortion using real-valued time-delay neural networks[A]. Proceeding of the 39th European Microwave Conference[C]. Rome, Italy, 2009.1149-1151.

[11] 瞿建峰, 周健义, 洪伟.有记忆的功放实数延时模糊神经网络模型[J]. 微波学报, 2009, 25(5): 41-43.QU J F, ZHOU J Y, HONG W. Real-valued time-delay neuro-fuzzy model for power amplifier with memory effects[J]. Journal of Microwaves,2009, 25(5):41-43.

[12] SALEH A. Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers[J]. IEEE Transactions on Communications,1981, 29(11):1117-1120.

[13] 张玉梅, 南敬昌.基于 Saleh函数的功放行为模型研究[J].微电子学与计算机, 2010, 27(12):121-126.ZHANG Y M, NAN J C.Study of behavior models based on the Saleh function for power amplifier[J]. Microelectronics and Computer, 2010,27(12): 121-126.

[14] JARDIN P, BAUDOIN G. Filter look up table method for power amplifiers linearization[J]. IEEE Transaction on Vehicular Technology,2007, 56(3):1996-1999.

[15] HAGAN M T, DEMUTH H B, BEALE M. Neural Network Design[M].Beijing: China Machine Press, 2002.197-235.

[16] BOSCH W, GATTI G. Measurement and simulation of memory effects in predistortion linearizers[J]. IEEE Transactions on Microwave Theory and Techniques, 1989, 37(12):1885-1888.

[17] CUI H, AI B, ZHAO X M.Design of a BPNN predistorter for nonlinear HPA with memory[J]. Journal of Information and Computational Science,2010, 7(4):863-868.

[18] ZAYNNI R, BOUALLENGUE R, ROVIRAS D. Adaptive predistortions based on neural networks associated with levenberg marquardt algorithm for satellite down links[J]. EURASIP Journal on Wireless Communications and Networking, 2008, 2008:132729.

[19] RAWAT M, RAWAT K. Adaptive digital predistortion of wireless power amplifiers/transmitters uing dynamic real-vlued focused timedelay line neural networks[J]. IEEE Transactions on Microwave Theory and Techniques, 2010, 58(1): 95-100.

[20] CUI H, ZHAO X M. A novel NN-predistorter learning method for nonlinear HPA[J]. Wireless Pres Commun, 2012, 63(2):469-482.

[21] MKADEM F, BOUMAIZA S. Physically inspired neural network model for RF power amplifier behavioral modeling and digital predistortion[J]. IEEE Transactions on Microwave Theory and Techniques,2011, 59(4): 913-922.

[22] RAWAT M, GHANNOUCHI F M. A mutual distortion and impairment compensator for wideband direct-conversion transmitters using neural networks[J]. IEEE Transactions on Broadcasting, 2012,58(2):168-176.

[23] 钱业青.一种高效的用于 RF功率放大器线性化的自适应预失真结构[J].通信学报, 2006, 27(5):36-39.QIAN Y Q. High-efficient adaptive predistortion structure for RF power amplifier linearization[J]. Journal on Communications, 2006,27(5): 36-39.

[24] HAGAN M T, MENHAJ M B. Training feed-forward networks with the marquardt algorithm[J]. IEEE Transactions on Neural Networks,1994, 5(6):989-991.

[25] FORESEE D F, HAGAN M T. Gauss-newton approximation to bayesian learning[A]. International Conference on Neural Networks[C]. Houston,TX, 1997.1930-1932.