基于链路重构—解构的端到端网络链路时延推测研究

梁永生，高波，邹粤，张基宏，张乃通

（1. 深圳信息职业技术学院 可视媒体处理与传输深圳市重点实验室，广东 深圳 518172；

2. 深圳大学 信息工程学院，广东 深圳 518060；3. 哈尔滨工业大学 电子与信息工程学院，黑龙江 哈尔滨 150001）

1 引言

网络时延是主要的网络性能指标之一，一般为数据从开始进入网络到离开网络的传输时间。在不同的传输介质和节点设备中，采用不同的网络架构和协议，网络时延大小也就不同，一般分为链路时延和节点时延2种，等于节点处理时延、排队时延、传输时延和传播时延四者之和。本文中的网络链路时延是指发生在不同地点的网络时延的统称。

网络链路时延推测是IP网络的热点研究问题。传统的网络链路时延推测是基于路由器或者路由器协作的，但是通常情况下，网络路由情况很难得到。端到端网络链路时延推测就是根据已经测量得到的端到端网络路径时延，推测出网络内部链路时延分布的过程，它能够克服传统方法的弊端。通过网络链路时延推测能够获知网络时延趋势、了解网络性能并可监控、规划和管理网络。

目前，国内外学者广泛采用最大似然估计方法(MLE, maximum likelihood estimation)推测网络链路时延，但是应用该方法存在以下2个主要问题。

1) 应用最大期望(EM, expectation maximization)算法求解似然函数，运算量过大，计算复杂度过高，实际推测环境难以及时反映网络状态的要求。

2) 网络拓扑结构和推测分组发送方式是时延推测有确定解的决定因素，如何确定适宜的发分组方式是需要重点考虑的问题。

基于上述分析，本文在2个假设——网络拓扑结构已知且稳定、链路性能时空独立的前提下，给出了网络时延推测模型和端到端路径时延数据采集方法，提出了一种基于链路重构—解构的端到端网络链路时延推测方法，首先应用伪似然估计将原推测问题分解为若干独立子问题分别求解。然后应用链路重构—解构确定可求解的推测单元，控制平均采样精度和减少推测单元链路数，从而显著降低计算复杂度。解决了计算复杂度过高及不满足有确定解拓扑下的求解问题。最后利用基于模型的计算和基于NS2的仿真实验进行了验证研究。

2 国内外研究现状

众多国内外学者对网络时延进行研究。文献[1]首次从硬件层面对IEEE标准容限内的以太网转发时延进行测试和分析，推导了以太网交换机内部转发时延和频偏时延的计算公式，进行了以太网交换机一次、二次转发时延测试，验证了时钟频偏是交换机转发时延的主要影响因素。文献[2]提出了一种启发式算法，采用离散时延模型对时延进行分片，但是计算复杂度较高。文献[3]提出了一种快速链路时延分布推测方法，首先基于网络子树分割技术，通过准确计算估计节点累积时延分布，然后由估计的累积时延分布得到单个链路时延分布；而且为了有效获取链路时延的本质特征，提出了一种可变二进制大小的离散链路模型。文献[4,5]提出了一种不需网络内部节点协作，依靠端到端测量推测链路时延累积量的方法，根据链路时延累积量和路径实验累积量的关系建立线性方程，然后求解方程得到链路时延累积量的最优估计值。文献[6]针对可以用指数随机变量模型来描述的网络链路时延，提出了一种最大似然估计器，应用EM算法，在初始参数不是很大的情况下，求解较快。文献[7]提出一种伪似然估计方法，降低了链路时延推测的指数级复杂度到，其中m为链路时延采样精度，P为路径的平均链路数，I为除发分组节点外的端节点数；西北工业大学的李贵山在伪似然估计算法的基础上，采用重采样技术优化时延分布结果[8]。文献[9]提出一种最优EM算法，但是以损失推测精度为代价。文献[10]提出用改进的蚁群算法来加快 EM算法的收敛速度，这种方法可以用于大型网络链路时延推测。文献[11]提出了一个面向单条链路的传输控制协议(TCP, transmission control protocol)综合传输性能测度R，分析其与同一时间粒度内链路的占用带宽和用户数据报协议(UDP, user datagram protocol)流量比例间的关系，结果表明R 测度可表示为以占用带宽和 UDP 流量比例为参数的正态分布的随机过程。在推测中，遵从本文的2个假设，把逻辑多播树转换为依赖树，从源节点发送探针分组，从叶子节点接收，采集端到端时延测量结果，推测链路的离散时延分布[12]。贝叶斯推断的基本方法是将待估参数的先验信息和样本的信息综合，然后根据贝叶斯定理得到其后验信息，接下来根据后验信息去推测未知参数。贝叶斯方法可以用于网络链路时延推测，但是推测的直接计算比较困难，目前一般的贝叶斯计算方法是 MCMC(Markov chain monte carlo)，其实质就是利用Markov Chain进行蒙特卡罗积分[13]。文献[14]基于主干网络时延测量，提出了一种应用主成份分析的网络时延结构分析方法，把网络时延时序分解为平滑的周期性态势和一组稀疏的突发流量。文献[15]提出了一种基于累积生成函数 (CGF, cumulative generating function)的逆函数法，利用最小二乘法求解链路时延，结果接近极大似然估计方法的估计值，但需要特殊的发分组方案以构造满秩路由矩阵。北京邮电大学交换技术通信网国家重点实验室在时延分布估计，分组丢失率估计和网络瓶颈推测等有比较深入的研究，焦利等应用 CGF方法来推测网络链路时延分布和确定网络的瓶颈链路[16]。文献[17]提出一种基于矩的估计方法，估计性能参数的N阶矩，但在计算中只对某些特定的时延分布函数有较高效率。文献[18]提出了一种改进的基于矩的估计方法，采用 MLE和EM-MLE推测网络链路时延，计算复杂度较高。文献[19]提出分层处理网络拓扑的方法，根据公共链路之间关系和协方差属性来估计链路时延数值，当链路时延差距较大时，推测精度较高。

综合国内外研究现状来看，如何降低伪似然估计算法的计算复杂度，并保证具有确定解，则成为网络链路时延推测研究的关键。

3 相关工作

3.1 时延推测前提

网络拓扑获取是链路时延推测算法中的首要问题，它决定了端时延特性与链路时延特性的映射关系。本文假设网络拓扑已知且稳定，网络拓扑结构的获取不列入本文研究内容。

假设在推测过程中，Xm(p)是链路m上第 p个推测分组的累积时延，随机变量Xm(p)服从某种分布[20]，则有

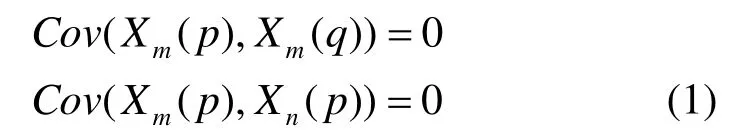
即不同推测分组p、q在同一链路m上的时延相互独立，同一推测分组p在不同链路m、n上的时延也相互独立。基于网络链路时空独立性假设，可以简化路径时延与链路时延的关系，路径时延分布可简单看作链路时延分布的卷积。

3.2 时延推测模型

时延推测网络模型如图1所示，0为发送节点，1和2是中间节点，3、4、5和6是接收节点。发分组节点与接收节点之间构成网络路径，发生在其上的网络时延构成路径时延向量DP。发分组节点与中间节点、中间节点与接收节点之间构成网络链路，发生在其上的网络时延构成链路时延向量DL。本文研究的网络链路时延推测就是根据路径时延向量DP，推测出链路时延向量DL。其中，A是所有推测网络路径对应的0-1路由矩阵，每一行对应一条推测网络路径，由网络拓扑结构唯一确定；ε是时延推测误差，在理想时延推测模型下，可以取ε=0。

图1 时延推测网络模型

网络时延是网络服务质量 (QoS, quality of service)中的加性参数，对于接收节点r有

其中，0,rPd 是在发送节点0到接收节点r的路径上测得的时延；di是以节点i为结尾的链路网络时延，且节点i在路径P0,r上。

由图1可知，A显然是4×6矩阵，为非满秩矩阵，这样向量DL无法通过向量DP与A的逆直接求解，这也正是本文研究的关键所在。

3.3 路径时延数据采集

对于路径时延数据采集，本文通过获取 ICMP（Internet control message protocol）协议返回的时间戳进行计算。图2为RTT(round trip time)示意，其中ST是发送时间戳，RT1是接收时间戳，RT2是返回时间戳，AT是传送时间戳。

图2 RTT示意图

通常情况下，发送端和接收端的系统时间不一致，所以不能简单地通过AT-ST来计算网络路径时延[21,22]。

为了更精确测得网络路径时延，本文以发送端的系统时间为基准，假定网络在传输数据分组的一段时间内保持稳定，则可利用数据分组往返时间的一半来计算网络路径时延，如式(4)所示。

4 PLE推测方法

由3.2节可知，端到端网络链路时延推测可以归结为一个统计逆问题，为了降低计算复杂度，现有的经典求解方法都是将原始的 MLE问题变换为PLE问题，将原来复杂的整体问题分解为一系列简单的子问题，并通过分别求解子问题从而获得整体问题的求解。

由此链路时延推测的似然函数如式(6)所示。

式(6)中参数θ的最大似然估计值通常通过最大化 Lp得到，但是由式(6)可知，直接通过(Lp;θ)'=0来求得θ是不易实现的。本文采用 EM 算法进行迭代求解。假设 XS是已知数据，且当前参数为θ(k)，则目标函数Q的第k+1次的取值为

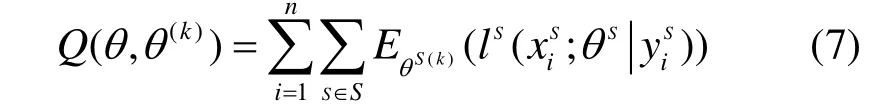
这样参数θ的最大似然估计值就可以通过最大化Q来得到。

本文中 Li表示以节点 i结尾的网络链路，表示第 m个推测分组在链路 Li上的网络时延，其中n为推测分组总数。在推测过程中，设链路Li上可能出现的最大时延和推测精度分别为q，令，则链路时延的可能取值为

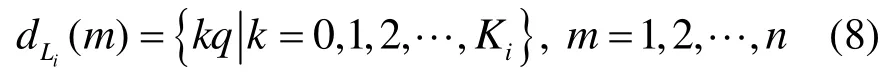
其中，k=0表示该推测分组在节点i上转发队列长度为 0。如果推测过程中发现分组丢失，则该次推测无效。对于iLd 的每一个取值，有

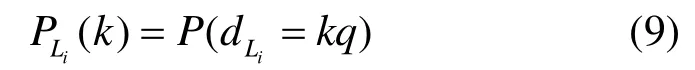
其中， PLi(k)表示链路Li上网络时延为kq的概率。在3.1节的假设前提下，推测分组时延和链路时延在时序上相互独立，这样本文研究的问题进一步转化为：由边缘接收节点组成的路径时延 DP的概率分布，推测网络内部链路时延DL的概率分布。

假设链路Li上传输ni个推测分组，其中时延为kq的推测分组数量为 ai(k)，则

实际上，ni可由选取的推测单元直接得到，而ai(k)不能直接得到。如果已知所有链路的时延概率分布 PL，则 ai(k)就有一个期望最大值。设有一个推测单元 u∈U，链路 Li在推测网络路径中，即，rx和ry为u的2个接收节点，在一次网络链路时延推测过程中，得到的时延二元组为

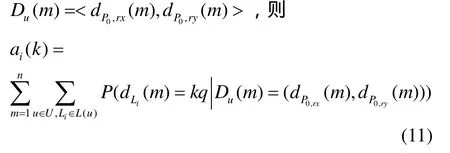
每一个推测单元的时延二元组构成一种输出模式，在推测过程中，假设该输出模式出现的次数为C(Du)，则式(11)变为

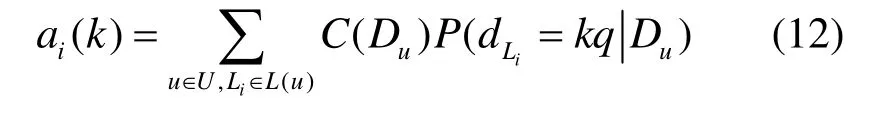
其中，C(Du)可以通过统计推测单元的观测数据得到，对于某一个推测单元的，有

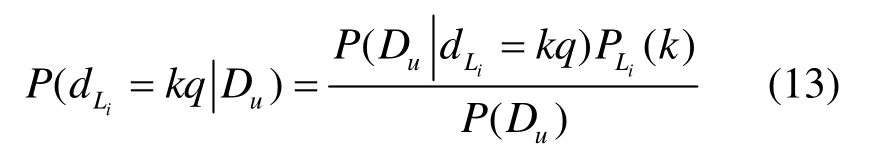
在链路Li上，设 dPf(i),rx、dPf(i),ry分别为其父节点f(i)到接收节点 rx、ry的网络时延。推测单元 u中的则可通过式(14)递推得到。

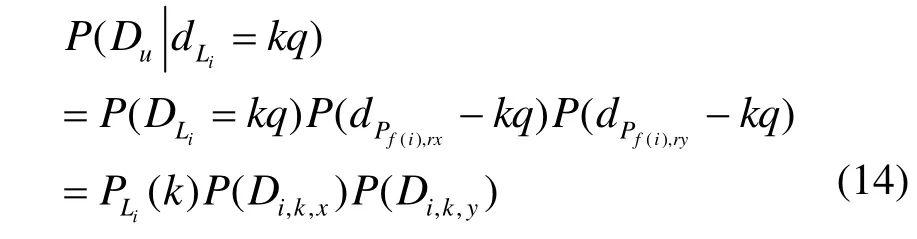
设节点i的直接子节点为d(i)，则

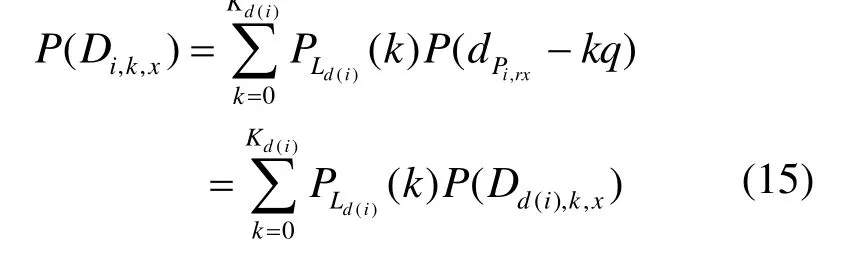
同理可求得 P (Di,k,y)。

当节点i为接收节点时，显然有

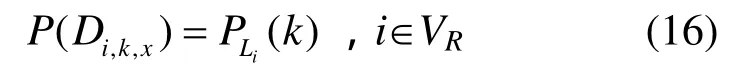
计算时，首先确定一个初始分布PL，然后应用式(12)迭代求解，直到推测误差小于预先设定值，则停止迭代，求解结束。

5 链路重构—解构算法

第4节中的PLE推测方法，虽然能够较为准确地推测出网络链路时延分布情况，但是仍有2个明显不足。

2) 推测网络必须满足每一个内部节点至少是一种推测单元的分支点，否则无法得到确定解。

为此，本文提出一种链路重构—解构算法，结合时延分发算法，在保证时延推测有确定解的同时，显著降低计算复杂度。

5.1 有确定解的推测方案

网络传输数据分组有单播和多播2种方式，简言之，单播就是一对一的通信方式，而多播就是一对多的通信方式。在时延推测过程中，通过一次发分组，多播方式可以获得多条推测路径，所以多播方式的推测效率比单播方式高，但是实际上多播方式在网络中的支持有限。

有确定解的推测方案是网络链路时延推测的基础，文献[23]给出了满足有确定解的推测方案的充要条件如下。

1) 每一个中间节点至少是一个 k(k>1)播推测单元的分支点。

2) 接收节点必须被一个或者多个推测单元覆盖。

由上述分析可知，推测方案有确定解的充要条件是当且仅当组成该推测方案的所有推测单元都有确定解。文献[24]提出了一种模拟多播方式，本文就采用其中的背靠背发分组方式获得路径时延数据。图3所示为本文采用的3种推测单元，图 3(a)由一条链路组成，显然推测单元的时延分布可以直接得到，所以这是有确定解的推测单元；图 3(b)是常见的二链路单元，它的时延分布与链路不是一一对应的，所以这是无确定解的推测单元；图 3(c)是最简单的有分叉网络，它的时延分布与链路是一一对应的，所以这也是有确定解的推测单元。

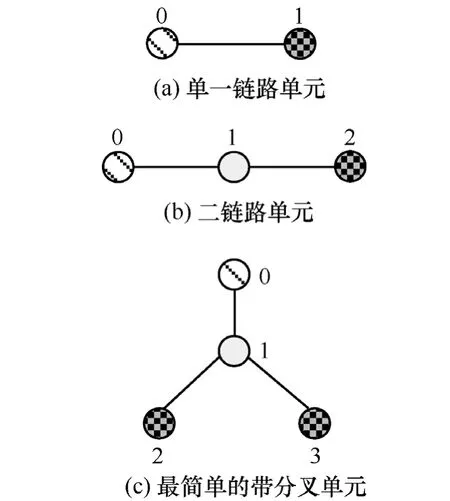
图3 推测单元

对于图3(b)，在链路时空相关性的假设下，首先推测包含节点 1的链路时延1LD ，然后推测包含节点1、2的路径时延(1,2)PD ，则包含节点2的链路时延2LD 为

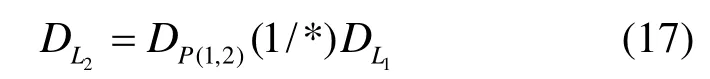
其中，(1/*)为反卷积运算。

5.2 链路重构—解构

所谓链路重构即是将首尾相连的若干链路看作一条逻辑链路，根据实际网络拓扑，可以在多处进行链路的重构，并不是所有首尾相连的链路都可以重构，重构的前提是重构后的逻辑链路仍然满足链路时延分布的独立性假设，重构的好处是可以降低计算复杂度；链路解构则是划分重构后的逻辑推测单元，使得由这些推测单元组成的推测方案满足有确定解的充要条件。

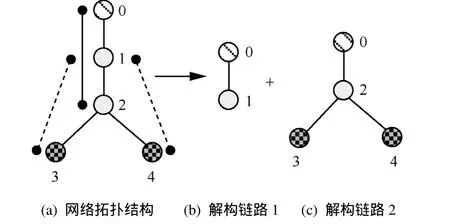
图4 链路重构—解构

实际上，对于每一种输出模式，建立对应的链路时延检索表，通过扫描该表可直接计算。对于网络中的一个推测单元，可采用一种自上而下的分配方法得到链路时延的可能集，其基本思想就是每次都把推测单元映射成三层树，接收节点为叶子节点，从第一条链路开始，每次确定一条链路的取值范围，最后得到时延向量集S，从而

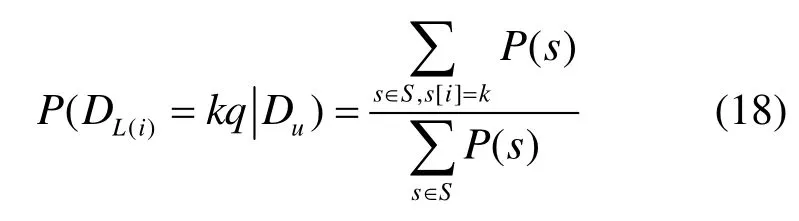
以图4所示的推测单元为例，链路时延集为四维向量，引入R(i)表示包含在节点i的子节点中的接收节点，时延分发流程如图5所示。

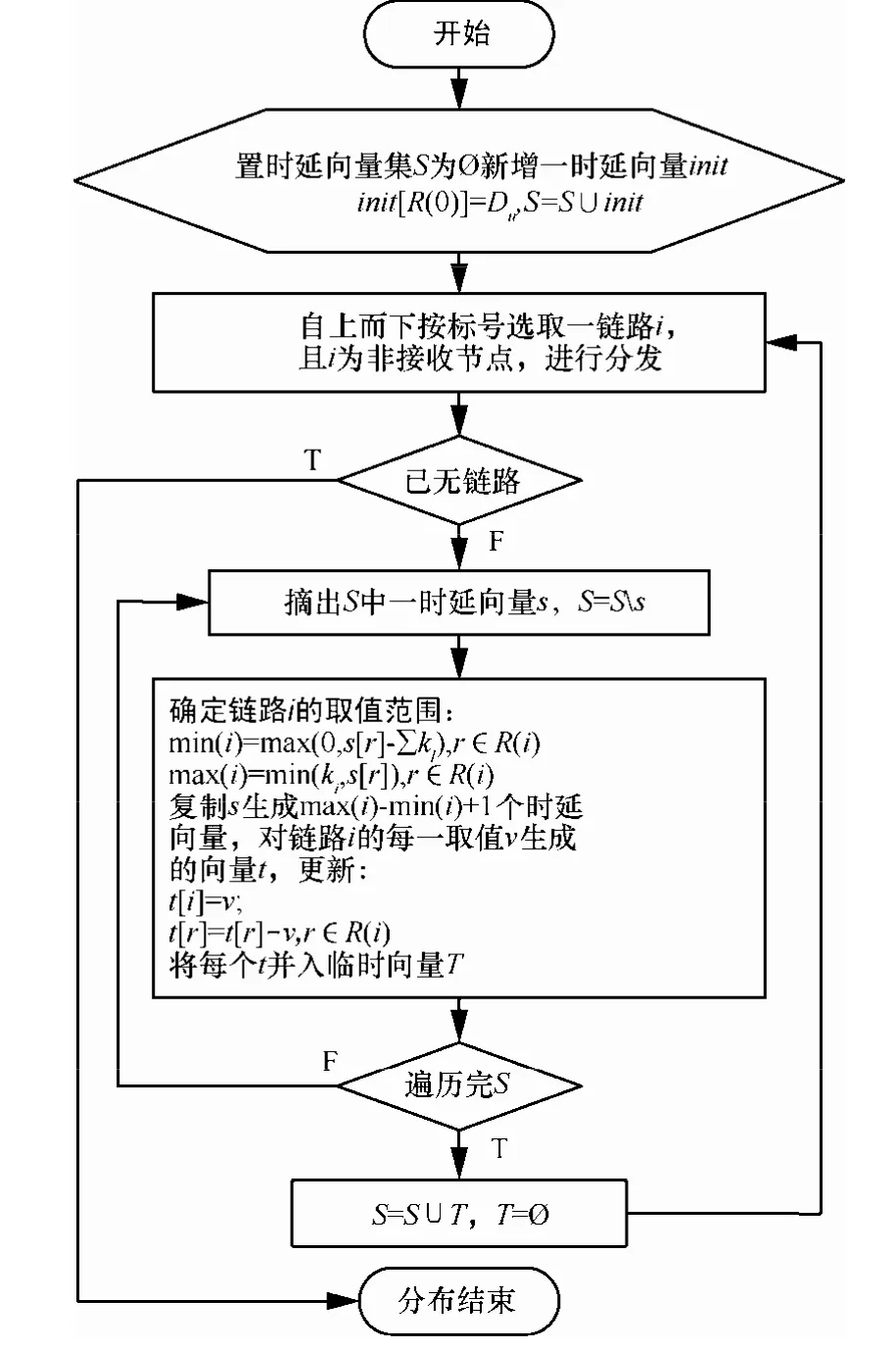
图5 时延分发流程

6 实验研究及结果分析

6.1 基于模型的计算

基于模型的计算，首先设定推测网络链路时延离散概率分布参数，然后应用赌轮算法生成对应的时延分布，保存网络路径时延数据，最后应用上述算法推测网络链路时延分布。

本文采用图6所示的网络拓扑结构进行实验研究，其中发分组节点 f是在图1上添加而来，节点 0、1和 2是中间节点，推测单元分别选择<3,4>和<5,6>，链路 L0的时延分布 PL0可直接得到。设定链路时延概率分布参数，由赌轮算法产生目标时延分布，随机选取某一推测单元的目标节点发送 10 000个推测分组，设定推测误差时迭代停止。很显然图 6中的网络拓扑结构不满足有确定解的条件，所以首先应用链路重构，然后解构出链路L1与L2，对应的时延分布为 PL1与 PL2，其中 PL2的推测结果如图7(a)所示。应用重构—解构推测的链路L3的时延分布PL3的推测结果如图7(b)所示。

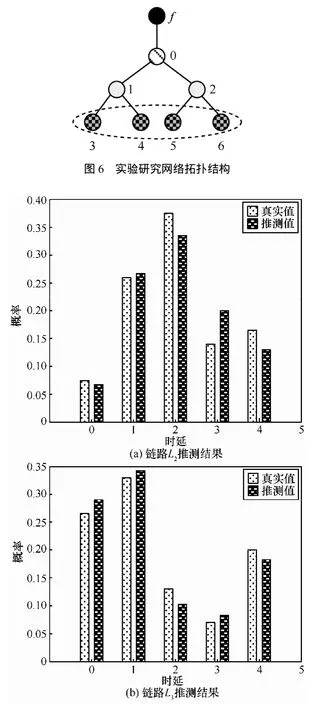
图7 链路时延推测结果

对于算法的收敛性，本文采用当前参数与上一次迭代所得参数的均方误差来判定算法每次迭代的收敛情况。当次间差值接近0且基本稳定时，则认为算法已找到极值。

由图7可知，k值不同时，推测值与真实值都较接近，这说明本文提出的算法是可行的。最大误差出现在链路2中，当K=3时，最大值为31.5%，这与初始值的选择有关。在以后的推测过程中，可以根据一定的先验知识，选取适当的初始值来解决这个问题，本文在初始时取均匀分布。通过基于模型的计算结果分析可知，本文提出的方法在网络链路时延推测方面具有应用价值，可为网络性能评价提供依据。

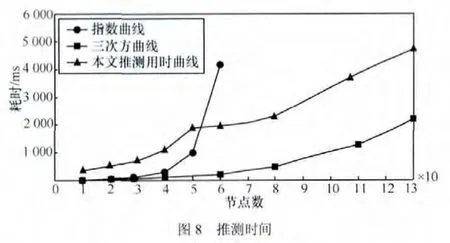
图8 推测时间

6.2 基于NS2的仿真

在图6中，各链路的带宽设置为：BL0=4 Mbit/s、BL1=2 Mbit/s、BL2=2 Mbit/s、BL3=1 Mbit/s、BL4=1 Mbit/s、BL5=1 Mbit/s和BL6=1 Mbit/s。采用固定码率(CBR,constants bit rate)发送背靠背推测分组模拟多播方式。为了模拟实际的网络环境，实验网络背景流量采用以下方式实现：在节点f上挂接一个1.5 Mbit/s的固定码率数据发送；在节点0上挂接2个FTP服务，分别连到接收节点 4、节点 6。网络链路的队列长度为10 000，在链路时延不断波动的情况下，尽量保证推测分组成功到达接收节点。在仿真实验研究中，链路 L0的带宽较宽、时延基本恒定，而其他链路的时延都会发生明显的变化。

在实验研究中，推测精度 q可从大到小进行尝试选取，直到目标链路时延分布精度满足要求为止。离散化网络时延时，通常通过观察闲时目标网络来确定0点，但是观察到的路径时延最小值不能直接作为0点，最佳值应为处理时延、传输时延和传播时延三者之和。为了方便起见，本文直接将观察到的最小路径时延作为 0点处理。

应用AWK脚本计算网络路径时延、统计网络链路真实的时延分布情况。链路1和链路3上推测得到的与真实的时延分布情况如图9所示。

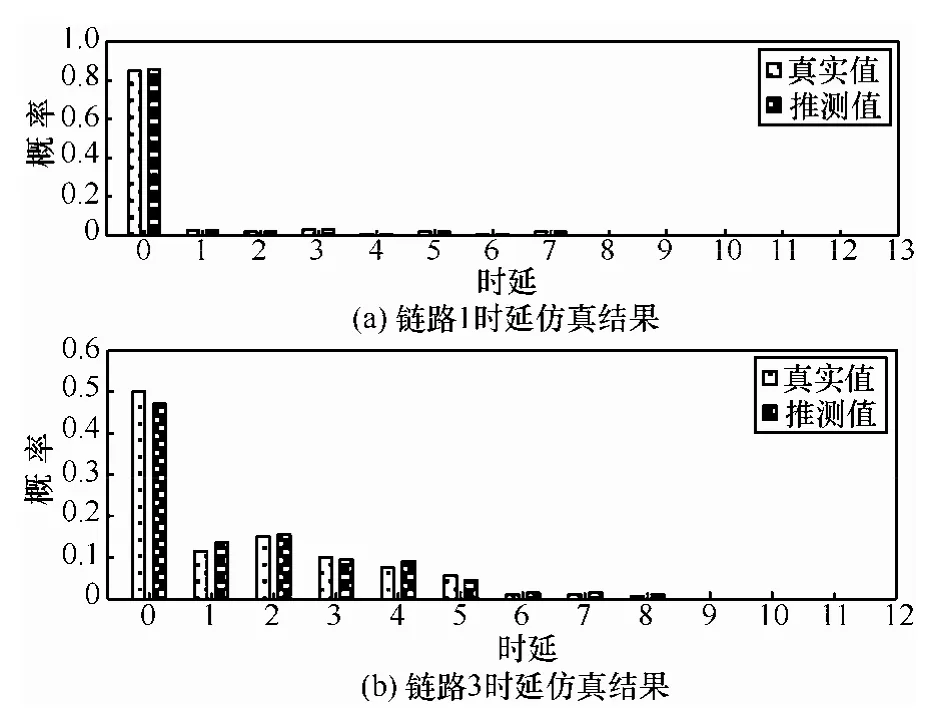
图9 链路时延仿真结果

由图9可知，k值不同时，推测值与真实值都较接近，最大误差出现在链路3中，当K=4时，最大值为22.5%，这与选取的q值有关。对于可变采样，时延变化较剧烈的链路3可采用更大的q值，本文取 q3=0.005，其他链路取 q=0.001。由于实际链路情况是未知的，q可从大到小试取，直到链路时延分布精度满足要求为止，达到精度与复杂度的平衡。由NS2仿真结果分析可知，本文提出的方法在网络链路时延推测方面具有应用价值，可为网络性能评价提供依据。

7 结束语

本文对端到端网络链路时延推测方法进行了研究，应用伪似然估计将原推测问题分解为若干独立子问题分别求解；应用链路重构—解构确定可求解的推测单元；通过控制平均采样精度和减少推测单元链路数，从而显著降低计算复杂度，解决了运算复杂度过高及不满足有确定解拓扑下的网络链路时延推测求解问题。理论分析和实验研究结果表明，基于链路重构—解构的端到端网络链路时延推测方法在保证有推测确定解的前提下，显著降低计算复杂度。与经典的基于CGF的网络链路时延推测算法计算复杂度相当，而且在推测过程中不必构造满秩路由矩阵。文中在2个假设的基础上对普遍意义上的网络模型进行链路时延推测研究，如何反映实际网络状况有待进一步研究。

[1] 梁永生, 张基宏, 张乃通. IEEE标准容限内以太网转发时延的测试与分析[J]. 电子学报. 2008, 36(1): 46-50.LIANG Y S, ZHANG J H, ZHANG N T. Measurement and analysis of forwarding delay in ethernet architecture within tolerances of the IEEE specifications[J]. Acta Electronica Sinica, 2008, 36(1): 46-50.

[2] PRESTI F L, DUFFIELD N G, HOROWITZ J, et al. Multicast-based inference of network-internal delay distributions[J]. IEEE/ACM Transactions on Networking, 2002, 10(6): 761-775.

[3] ZHANG Z Y, FEI G L, PAN S L, et al. A fast link delay distribution inference approach under a variable bin size model[J]. IEICE Transactions on Communications, 2013, E96-B(2): 504-507.

[4] FEI G L, HU G M, JIANG X Y. Unicast-based inference of network link delay[A]. Proceedings of the 13th IEEE International Conference on Communication Technology (ICCT)[C]. Jinan, China, 2011. 146-150.

[5] 蒋小勇, 费高雷, 胡光岷. 网络链路时延统计量的层析成像方法[J].计算机工程与应用, 2012, 48(3): 91-94, 208.JIANG X Y, FEI G L, HU G M. Network link delay statistics tomography[J]. Computer Engineering and Applications, 2012, 48(3):91-94, 208.

[6] XIA Y, TSE D. Inference of Link delay in communication networks[J].IEEE Journal on Selected Areas in Communications, 2006, 24(12):2235-2248.

[7] LIANG G, YU B. Maximum pseudo likelihood estimation in network tomography[J]. IEEE Transactions on Signal Processing, 2003, 8(51):2043-2053.

[8] 李贵山, 蔡皖东. 网络链路时延分布估计方法研究[J]. 计算机工程与应用, 2009, 45(8): 20-22, 28.LI G S, CAI W D. Research on method for estimation of network link delay distributions[J]. Computer Engineering and Application, 2009,45(8): 20-22, 28.

[9] TSANG Y, COATES M, NOWAK R D. Network delay tomography[J].IEEE Transactions on Signal Processing, 2003, 8(51): 2125-2135.

[10] SUN H J. An improved ant-based EM algorithm for network link delay distributions inference[A]. Proceedings of the 2nd International Workshop on Education Technology and Computer Science(ETCS)[C].Wuhan, China, 2010. 48-51.

[11] 朱海婷, 丁伟, 缪丽华等. UDP 流量对 TCP 往返延迟的影响[J].通信学报, 2013, 34(1): 19-29.ZHU H T, DING W, LIAO L H, et al. Effect of UDP traffic on TCP’s round-trip delay[J]. Journal on Communications, 2013, 34(1): 19-29.

[12] 刘瑞芳, 谢东. 采用多播依赖树模型估计链路时延分布[J]. 信息工程大学学报, 2007, 8(4): 422-424.LIU R F, XIE D. Using dependence tree model for network delay tomography[J]. Journal of Information Engineering University, 2007,8(4): 422-424.

[13] GUO D, WANG X D. Bayesian inference of network loss and delay characteristics with applications to TCP performance prediction[J].IEEE Transactions on Signal Processing, 2003, 8(51): 2205-2218.

[14] ABDELKEFI A, JIANG Y M. A structural analysis of network delay[A]. Proceedings of the 2011 Ninth Annual Communication Networks and Services Research Conference[C]. Ottawa, Canada,2011. 41-48.

[15] SHIH M F, HERO A O. Unicast inference of network link delay distributions from edge measurements[A]. Proceedings of the IEEE International Conference on Accost Speech and Signal Processing[C].Salt Lake City, USA, 2001. 3421-3424.

[16] 焦利, 林宇, 王文东等. 一种负载均衡网络中内部链路时延估计算法[J]. 软件学报, 2005, 16(5): 886-893.JIAO L, LIN Y, WANG W D, et al. A novel algorithm for link delay inference in the networks with load-balancing routing[J]. Journal of Software, 2005, 16(5): 886-893.

[17] LAWRENCE E, MICHAILIDIS G, NAIR V N. Fast, moment-based estimation methods for delay network tomography[J]. IEEE Transactions on Signal Processing, 2008, (9): 1-22.

[18] LIN J W, ZHANG J Z, LIN W. The improved method of moment for multicast-based delay distribution inference in network tomography[A].Proceedings of 2010 2nd International Conference on Advanced Computer Control(ICACC)[C]. Shenyang, China, 2010. 486- 489.

[19] LIN J W, ZHANG J Z. A High-efficiency algorithm for delay estimate in network tomography[J]. Journal of Computational Information Systems , 2010, 6(10): 3217-3226.

[20] COATES M, HERO A O, NOWAK R D, et al. Internet tomography[J].IEEE Signal Processing Magazine, 2002, 19(3): 47-65.

[21] LIANG Y S, ZHANG N T. The determination of the link with the smallest end-to-end network latency in ethernet architecture[J].Journal of Harbin Institute of Technology, 2007, 14(4): 489-495.

[22] CHOI J H, YOO C. Analytical derivation of one-way delay[J].Electronics Letters, 2003, 39 (25): 1871 -1872.

[23] LAWRENCE E, MICHAILIDIS G, NAIR V N. Network delay tomography using flexicast experiments[J]. Journal of the Royal Statistical Society, Series B, 2006, (68): 785-813.

[24] COATES M, NOWAK R D. Network tomography for internal delay estimation[A]. Proceedings of the IEEE International Conference on Accost Speech and Signal Processing[C]. Salt Lake City, USA, 2001.3409-3412.