一种埋入型PZT的三维等效机电阻抗模型——第一部分:理论

左春愿，冯 新，周 晶

(大连理工大学 建设工程学部，辽宁 大连 116024)

机电阻抗(EMI)技术是近年来出现的一种智能结构健康监测技术，其基本原理是:结构固有属性的改变引起结构机械阻抗变化，通过对结构机械阻抗的监测即可实现对结构固有属性改变的探测。然而，结构机械阻抗往往难以直接获得。EMI技术利用压电材料的机电耦合效应，给埋入或粘贴于结构上的压电陶瓷(PZT)施加高频激励，使结构产生高频局部机械振动，这一振动通过压电效应在PZT内产生电信号，然后通过测量分析PZT与结构耦合电阻抗来获得结构的机械阻抗，实现对结构固有属性的分析研究。EMI技术因对结构微小变化敏感、可隔离环境或远程荷载、成本低等特点在结构健康监测和损伤探测中得到了越来越多的关注［1］。近年来，该技术被广泛应用于各种类型结构的在线监测。Park等［2］利用EMI技术监测到砌体构件中的初始裂缝。Park等［3］采用EMI技术对管道结构进行损伤识别。Soh等［4］运用EMI技术对一个钢筋混凝土桥梁进行监测，验证了EMI技术能够监测混凝土结构中初始损伤及损伤的发展情况。

PZT传感元件与结构间的相互作用，是实现机电阻抗测量的基础，也是传感器设计以及测量信号分析的关键，因此PZT－结构的相互作用分析模型研究具有重要意义。目前，对智能结构体系进行动态响应分析的方法主要有三种，分别为静力等效法、动力有限元法以及阻抗建模法。静力等效法假定PZT与基体结构之间的相互作用是位于PZT端部的集中力，其与激励频率无关。通过PZT与结构的位移协调方程和静力平衡方程求解该力，然后用该力求解结构的静动力响应。对于PZT质量与刚度敏感的结构而言，该方法不能求得可靠的结果［5］。动力有限元法是数值求解中应用较为广泛的一种，是结构动态响应分析的有效手段。但是其存在不足之处，例如，没有反映PZT与结构相互作用的物理本质;为了满足收敛性，在PZT周围需要很精细的网格划分，导致计算效率较低［5］。

阻抗模型分析法是PZT与结构相互作用分析研究中一类重要的方法，它具有物理意义明确、可获得分析解答、计算效率高等特点，而成为当前国内外的研究热点之一。阻抗模型分析法的基本原理为:PZT与基体结构相互作用是由PZT动态输出特性Za(PZT的机械阻抗)与结构的动态特性Zs(结构的机械阻抗)决定的，其反映出PZT与基体结构相互作用的物理本质［5］。Liang等［6－7］首先从理论上建立了PZT与结构系统构成的单自由度弹簧－质量－阻尼系统(SMD)模型，推导出PZT与一维SMD系统的耦合电导纳表达式，分析了结构机械阻抗的变化对耦合电导纳的影响，并以悬臂梁为例进行了验证。Zhou等［8］在PZT与一维SMD系统阻抗模型基础上，建立了二维PZT与基体结构耦合的阻抗模型，得到了相应的耦合电导纳表达式。Bhalla等［9－11］将 PZT 看作是无限小的，可忽略质量和刚度的有效驱动点，有效驱动点的阻抗称为等效机械阻抗。等效机械阻抗的引入，简化了PZT与基体结构的相互作用模型，并以此推导出了耦合电导纳表达式。随后利用该方法对一个航空结构构件的试验模型进行了损伤诊断，证实了该方法的有效性。

对于大型混凝土结构，其内部情况复杂却无法得知。因此，通过埋入混凝土结构内部的PZT传感器来反映混凝土结构的动态响应，达到对混凝土结构内部变化的监测。由于一维与二维模型忽略了PZT纵向振动对相互作用的影响，不符合埋入型PZT传感器的振动模态，因此建立三维PZT与结构耦合分析模型具有重要意义。Annamdas等［12－13］在同时考虑 PZT的纵向振动和横向振动基础上，建立了三维机电阻抗模型，并分析得到了总电导纳方程。但是，所得到的方程式很复杂，无法明确体现PZT机械阻抗及结构机械阻抗对耦合电导纳的影响，不便于实际应用，且在研究过程中忽略了压电材料的各向异性。因此，本文在考虑压电材料各向异性的基础上，利用等效机械阻抗原理，建立了一种PZT传感器与结构相互作用的三维等效机电阻抗模型，推导出三维PZT驱动系统的耦合电导纳方程，这一方程明确体现了PZT等效机械阻抗Za，eff与结构等效机械阻抗Zs，eff对耦合电导纳的贡献。由此耦合电导纳方程，得到自由PZT电导纳理论值，并进行了自由状态PZT的分析验证。

1 结构的机械阻抗

一个稳定的线性振动系统，在简谐交变力F(t)作用下所产生的稳态响应x(t)(位移、速度或加速度)，必定是同频率的谐振动。但一般来说，响应总要滞后于激励。结构机械阻抗定义为简谐激励与其所引起的稳态响应是复数比，其倒数称为机械导纳［14］。

按照机电比拟，机械量(力和速度)与电量(电压和电流)可以相比拟，则一般所说的机械阻抗和机械导纳，指的是速度阻抗和速度导纳，即结构产生的稳态响应以速度形式来表示。

假设结构所受到的激振力为:

式中，Fo为激振力的幅值，ω为激振力的圆频率。由此产生的稳态响应为:

式中，u·o速度响应的振幅，φ为速度响应的初相角。则该结构的机械阻抗Z，可以表示为:

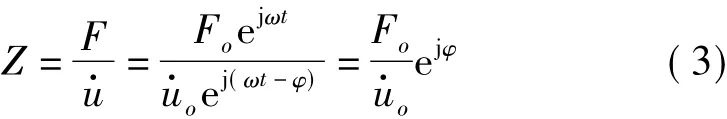
式中，机械阻抗幅值为|Z|=Fo/u·o，相位角为 φ。

图1 圆形PZT片几何图Fig.1 The geometry of the circular PZT patch

2 三维等效机电阻抗模型

在已有的机电阻抗模型分析中，一般假定PZT的振动是一维或二维的，对 PZT厚度有很大限制，并且忽略了纵向振动对结构动力响应的影响。因此，更准确的三维机电阻抗模型的建立具有重要意义。

2.1 圆形PZT片的基本方程

图1所示为一圆形片状压电陶瓷，R、2h分别为其径向半径和轴向高度，极化方向沿其高度即Z轴方向，电极面垂直Z轴。在研究中，圆形PZT的几何尺寸不加任何限制，关注径向振动模式与纵向振动模式的耦合振动。考虑压电材料的各向异性，存在以下关系式圆形PZT在柱面坐标中的压电方程为［15－16］:

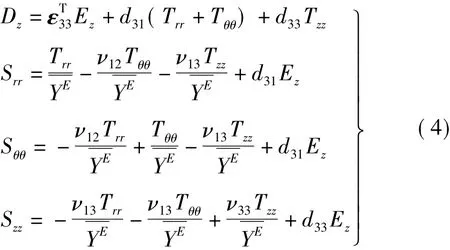
式中，λ =1 －ν12－ν13+n(ν33－2ν13)。

求解PZT运动方程，可以得到PZT径向位移为:

同理，可以得到PZT纵向位移为:

对于有限尺寸压电陶瓷圆片的耦合振动，在多模振动以及自由边界条件下，可得其厚度及径向的耦合振动频率方程为［19］:

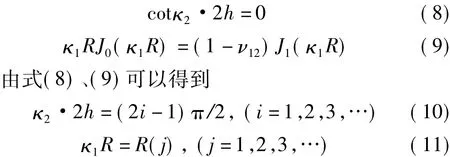
式中，R(j)为式(9)的根，它是 ν12的函数;i，j是正整数，对应PZT的各次振动模式。将波数κ1，κ2代入式(10)、(11)可以得到

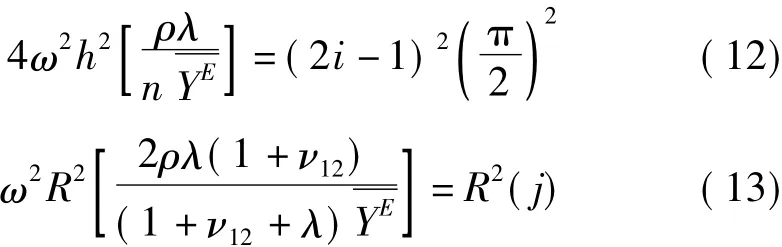
根据式(12)、(13)可以消去与频率相关项ω2，并结合 λ =1－ν12－ν13+n(ν33－2ν13)得到机械耦合系数n的方程式:

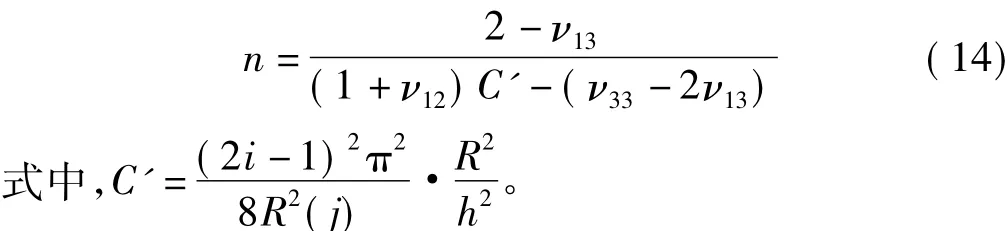
2.2 等效机械阻抗的定义

传统阻抗模型将PZT与基体结构之间的连接看作一个特殊点，这一特殊点就是PZT的端点。然而，实际中PZT与基体结构的相互作用并不局限于该点上，而是遍布在PZT表面上。考虑到这一点，Bhalla等［10］提出了等效机械阻抗概念，即将PZT看作是无限小的，可忽略质量和刚度的有效驱动点，有效驱动点的阻抗称为等效机械阻抗。并将其应用于分析二维等效阻抗模型。将其进行进一步扩展，可以得到三维等效阻抗模型。

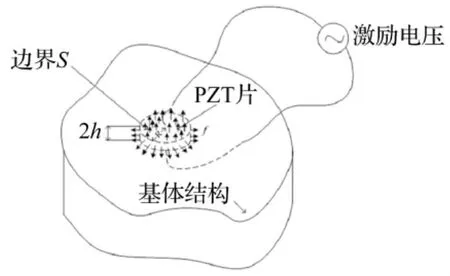
图2 埋入未知结构的PZT片的示意图Fig.2 Host structure with embedded PZT patch

将有限大小的圆形PZT埋入基体结构中，如图2所示。给PZT一个空间均匀的电场激励，则PZT产生简谐振动。PZT的半径为R，厚度为2 h。PZT与结构之间的相互作用表现为边界面上每平方f的牵引力，平面力在PZT中产生了位移。假定PZT与主体结构之间的相互作用力是沿整个边界面传递的，同时PZT与主体结构相比是无限小的圆片，可以忽略其质量和刚度，可以得到有效驱动点的机械阻抗为:

2.3 基于等效阻抗的耦合电导纳方程

埋入结构中PZT圆片受力情况如图3所示，其半径及厚度分别为R和2 h，上下端面涂满电极，沿着其厚度方向极化，电场沿厚度方向施加。极化方向与所加电场的方向平行，那么，PZT的振动主要为伸缩振动，可以忽略剪切振动。得到PZT的速度和应变的关系为:

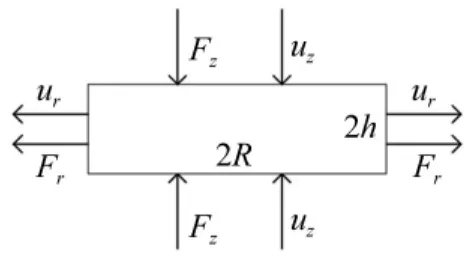
图3 埋入型PZT圆片受力情况Fig.3 Force situation of embedded circular PZT patch

上式对时间求导，可以得到PZT片的等效速度表达式为:

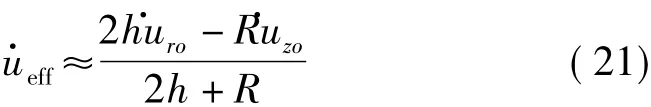
由于PZT处于多维耦合振动状态，那么在任何瞬间，PZT在径向膨胀的同时在Z轴方向是收缩的。反之，其在径向收缩那么在Z轴方向膨胀。为了简化计算，假定存在以下关系:

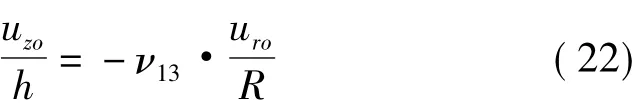
将式(6)，(7)代入式(22)可以得到以下关系式:

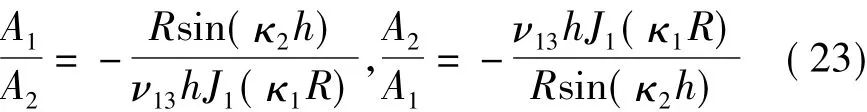
通过式(15)可以计算得到PZT的等效机械阻抗为:

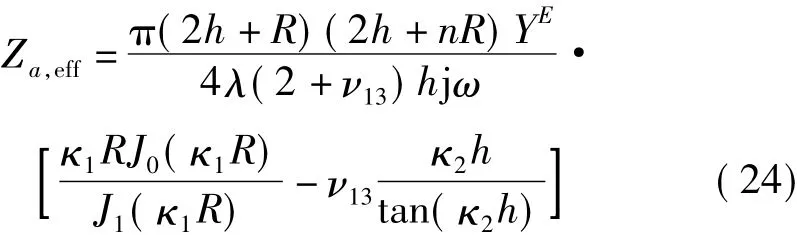
主体结构有效驱动点的等效力F可以通过下式表示:

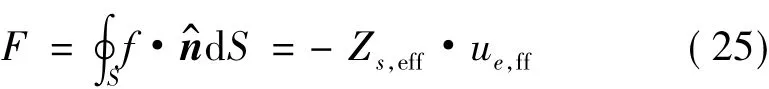
式中，负号表示积极等效位移在PZT上产生了压力。将式(16)，(17)，(18)，(19)以及 Ez=(Vo/2h)ejωt代入上式可以得到:

瞬时电流可以表示为通过某一截面的电量Q(t)对时间t的导数，则可以表示为:

将式(4)，(5)，(26)代入上式，并进行积分，r方向积分范围为0到R，θ方向积分范围为0到2π，电导纳由电流与电压的比值表示为:

这一方程明确体现了PZT等效机械阻抗Za，eff与结构等效机械阻抗Zs，eff对耦合电导纳的影响。因此，由式(28)可以推导出结构等效机械阻抗Zs，eff，这使得从所测得的耦合电导纳中提取结构机械阻抗成为可能。PZT与基体结构所组成的耦合结构体系中，PZT材料参数不变，则 Za，eff不变。那么基体结构等效机械阻抗Zs，eff的变化直接引起耦合电导纳的变化。反之，耦合电导纳的变化反映出基体结构的固有属性发生了改变。

3 自由PZT电导纳分析

前文基于等效阻抗的概念，得到了圆形PZT与结构耦合的电导纳方程式。由式(28)可知，实测的耦合电导纳包含了结构等效机械阻抗和PZT等效机械阻抗的贡献。当已知PZT的几何尺寸和基本参数时，耦合电导纳只依赖于结构等效机械阻抗和PZT等效机械阻抗，因此PZT等效机械阻抗的精度直接影响结构等效机械阻抗的估计精度。但PZT等效机械阻抗无法通过实际测量得到，只能在已知PZT的几何尺寸和材料参数情况下，通过式(24)进行计算。为精确地估计PZT的等效机械阻抗，PZT基本参数的精度是需要验证的。

表1 PZT的基本参数Tab.1 Properties of PZT patch

已知PZT的基本参数，通过式(31)可以计算得到自由状态下PZT的电导Gf和电纳Bf。文中所采用的圆片状PZT直径为20 mm，厚度为2 mm，基本参数如表1所示。根据式(31)，可以得到频率范围为0－350 kHz时自由PZT电导曲线和电纳曲线，如图4所示。另外，自由PZT的电导纳信号可以利用Agilent4294A精密阻抗分析仪来直接测得。图4中所示的电导G与电纳B即为实际测量的频率范围为0－350 kHz时自由PZT电导纳信号。

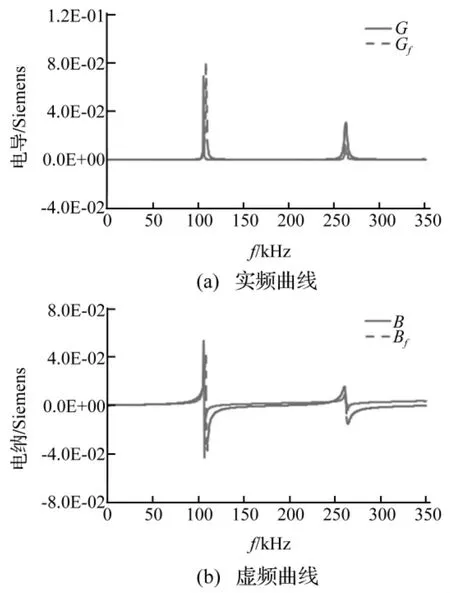
图4 自由PZT电导纳信号实测值与理论值Fig.4 Comparison between experimental and theoretical signals of PZT patch in free－free condition

图4 中描述的是，频率范围为0－350 kHz时自由PZT电导纳信号实测值(G，B)与理论值(Gf，Bf)的对比。通过对比可以看出，自由PZT电导纳理论值与实测值曲线形状相似。理论上的共振频率和实测值很接近，理论值大于实测值，第一个共振频率点比第二个共振频率点吻合性更好。总体来说，自由PZT电导纳理论分析值与实测值具有较好的一致性。研究发现理论值与实测值存在一定误差。这说明了受生产工艺以及PZT与导线焊接过程中高温的影响，生产厂家提供的部分PZT参数并不可靠。因此，需要利用实测的耦合电导纳信号，通过自由PZT电导纳方程式，来计算出更精确的PZT相关参数值，并用计算的参数来估计PZT等效机械阻抗。最终，利用式(28)得到较为精确的结构等效机械阻抗。

4 结论

本文第一部分首先基于PZT三维耦合振动的原理，建立了埋入型PZT传感器与结构相互作用的三维等效机电阻抗模型。然后通过引入等效机械阻抗的概念，得到PZT与结构耦合电导纳方程，该方程描述了耦合电导纳与结构机械阻抗的关系。利用耦合电导纳方程，得到自由PZT电导纳理论值，并进行了自由状态PZT的分析验证。三维等效机电阻抗模型的提出，使PZT厚度不受限制，提高了试验的成功率;并且考虑PZT的多维耦合振动对结构动力响应的影响，使分析更加贴近实际。同时，PZT不再局限粘贴于结构表面，结构内部的变化也能得到监测，扩大了EMI技术的使用范围。本文第二部分提出应用EMI技术监测结构固有属性的改进方法。该方法通过耦合电导纳方程，提取结构机械导纳。利用得到的结构机械导纳，来监测结构固有属性。

［1］朱宏平，王丹生，张俊兵.基于压电阻抗技术的结构损伤识别基本理论及其应用［J］.工程力学，2008，25(SⅡ):34－43.ZHU Hong-ping， WANG Dan-sheng， ZHANG Jun-bing.Theory and application of structure damage detection based on piezoelectric impedance technique ［J］. Engineering Mechanics，2008，25(SⅡ):34－43.

［2］Park G，Cudnery H H，Inman D J.Impedance-based health monitoring of civil structural components［J］.Journal of Infrastructure Systems，2000，6(4):153 －160.

［3］Park G，Cudnery H H，Inman D J.Feasibility of using impedance-based damage assessment for pipeline structures［J］.Earthquake Engineering and Structural Dynamics，2001，30(10):1463－1474.

［4］Soh CK，Tseng K K-H，Bhalla S，et al.Performance of smart piezoceramic patches in health monitoring of a RC bridge［J］.Smart Material and Structure，2000，9(4):533 －542.

［5］Liang C，Sun F P，Rogers C A.An impedance method for dynamic analysis of active material systems［J］.Journal of Vibration and Acoustics，1994，116(1):120－128.

［6］Liang C，Sun F P，Rogers C A.Coupled electromechanical analysis of piezoelectric ceramic actuator-driven systemsdetermination of the actuator power consumption and system energy transfer［J］. Smart Structures and Intelligent Systems，1993，1917:286－298.

［7］Liang C，Sun F P，Rogers C A.Coupled electro-mechanical analysis of adaptive material systems-determination of the actuator power consumption and system energy transfer［J］.Journal of Intelligent Material Systems and Structures，1994，5(1):12－20.

［8］ Zhou S，Liang C，Rogers C A.Integration and design of piezoceramic elements in intelligent structures［J］.Journal of Intelligent Material Systems and Structures，1997，8(4):363－373.

［9］Bhalla S，Soh C K.Structural impedance based damage diagnosis by piezo-transducers［J］.Earthquake Engineering and Structural Dynamics，2003，32(12):1897 －1916.

［10］ Bhalla S，Soh C K.Structural health monitoring by piezoimpedance transducers. Ⅰ: Modeling［J］. Journal of Aerospace Engineering，2004，17(4):154－165.

［11］ Bhalla S，Soh C K.Structural health monitoring by piezoimpedance transducers.Ⅱ:Applications［J］.Journal of Aerospace Engineering，2004，17(4):166－175.

［12］ Annamdas V G M， Soh C K. Three-dimensional electromechanical impedance model.Ⅰ:Formulation of directional sum impedance［J］. Journal of Aerospace Engineering，2007，20(1):53－62.

［13］ Annamdas V G M， Soh C K. Three-dimensional electromechanical impedance model.Ⅱ:Damage analysis and PZT characterization ［J］. Journal of Aerospace Engineering，2007，20(1):63－71.

［14］左鹤声.机械阻抗方法与应用［M］.北京:机械工业出版社，1987.

［15］IEEE Std 176－1987，An American national standard IEEE standard on piezoelectricity［S］.New York:The Institute of Electrical and Electronics Engineers，Inc，1987.

［16］张福学，王亚坤.现代压电学(上册)［M］.北京:科学出版社，2001.

［17］林书玉.压电陶瓷圆片振子耦合振动的等效电路［J］.压电与声光，1993，15(6):32 －37.LIN Shu-yu.The equivalent circuit of coupled vibration for piezoelectric ceramic disks［J］. Piezoelectrics and Acoustooptics，1993，15(6):32－37.

［18］Meitzler A H，O’Bryan H M，Tiersten H F.Definition and measurement of radial mode coupling factors in piezoelectric ceramic materials with large variations in Poisson’s ratio［J］.IEEE Transactions on Sonics and Ultrasonics，1973，20(3):233－239.

［19］林书玉，张福成.压电陶瓷圆片振子的多模耦合振动［J］.电子学报，1994，22(12):64－69.LIN Shu-yu，ZHANG Fu-cheng.Multimode coupling vibration in disk plates of piezoelectric ceramics［J］.Acta Electronica Sinica，1994，22(12):64－69.