超高速撞击声发射信号在加筋壁板中传播的模态转换现象研究

刘治东，庞宝君，刘 刚

(1.哈尔滨工业大学，哈尔滨 150001;2.中国空间技术研究院，北京 100094)

随着人类空间活动的增多，空间碎片环境日益恶化，严重威胁航天器，特别是载人航天器的在轨安全运行［1］。为此，人们提出了多种基于不同技术基础的空间碎片在轨感知系统方案［2］，用于实时监测空间碎片撞击航天器事件。其中，一种基于声发射的在轨感知系统具有被动接受、环境适应性强、信息丰富等特点，受到了重视与研究［3－4］。该系统通过安装在舱壁表面的换能器采集空间碎片撞击密封舱产生的超高速撞击声发射信号，从而感知、定位撞击事件。为发展声发射在轨感知技术，有必要对声发射信号在舱壁中的传播特性进行研究。

为追求结构轻量化，密封舱通常由整体周期性加筋壁板焊接而成，其表面具有大量加强筋、隔框等多种形式的凸起。超高速撞击声发射信号本质是在靶板中传播的板波，当其经过筋体等凸起时会发生散射现象。板波在传播介质表面凸起处会发生散射现象是声发射领域中的一项重要研究课题。

目前，研究人员主要对单一模态板波的散射现象开展了研究工作，其中对低阶对称板波(S0)和反对称板波(A0)在结构凸起处的散射现象的研究已取得了一定进展［5－11］。研究发现，板波传播到达凸起处时会发生透射及反射现象，其中部分透射波还会发生模态转换现象，如图1所示。其中，S0波会部分转换为A0波，A0波会部分转换为S0波。图中S0A0、A0S0分别表示由S0、A0阶板波转换而来的A0、S0阶板波。

但是，目前尚缺乏对更高阶模态板波，特别是二阶对称板波S2的模态转换特性的研究。而超高速撞击声发射信号包含S0、A0和S2等3种模态的板波。因此，为了研究超高速撞击声发射信号在舱壁中的传播特性，本文将采用数值仿真手段，针对超高速撞击声发射信号，特别是S2阶板波在凸起处的模态转换特性，开展研究工作。

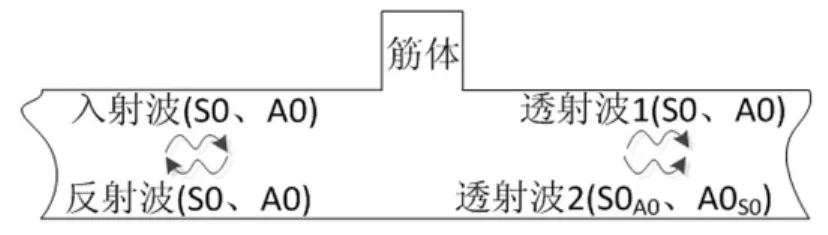
图1 加筋板中的板波散射现象Fig.1 Scattering phenomenon of lamb wave in stiffened plate

1 数值仿真

在超高速撞击声发射技术领域，目前多采用AUTODYN 软件进行数值模拟，如刘武刚［12］和唐颀［13］分别采用Lagrange算法和光滑粒子流体动力学方法(SPH算法)建立了单弹丸超高速撞击铝合金平板二维轴对称模型，Wicklein等［14］采用 Lagrange+SPH 算法建立了单弹丸超高速撞击蜂窝夹芯层合板三维模型。综合参考上述3种建模方法，本文选择采用AUTODYN软件，Lagrange算法，建立二维轴对称模型，进行数值模拟。

1.1 材料模型

在AUTODYN软件中，材料模型包含物态方程、强度方程和失效模型等3部分，共同描述材料物理特性。本文引用了唐颀［13］给出的材料参数，其中物态方程采用Mie-Gruneisun方程，如式(1)所示，其参数如表1所示。

式中，p和e分别为静水压力和比内能;pH和eH分别为冲击Hugoniot曲线上静水压力和比内能的参考值;Γ和ρ分别为 Gruneisun参数和密度，Γ0和 ρ0为初始Gruneisun参数和初始密度;U和up分别为冲击波波速和波后质点速度，c0为体积声速，s为U和up之间线性关系的斜率;μ为压缩比。

表1 Mie-Gruneisun状态方程材料参数Tab.1 Material parameters of Mie-Gruneisun equation of state

强度模型采用Johnson-Cook模型，模型参数如表2所示，其屈服应力σy与等效塑性应变εp、等效塑性应变率和温度T之间的关系为

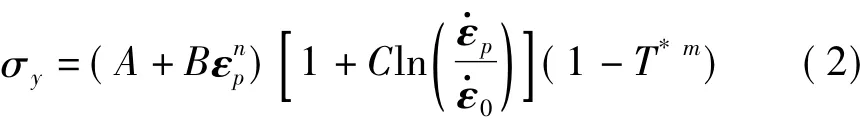
式中，参考应变率=1s－1;A、B、n、C和m是材料常数，A为材料在准静态下的屈服强度，B和n为应变硬化的影响，C为应变率敏感指数，m为温度软化系数。若室温为TRoom，熔点为TMelt，则同系温度的定义为

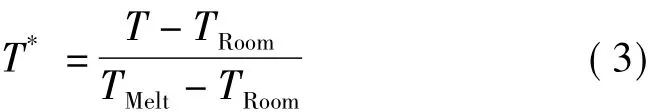
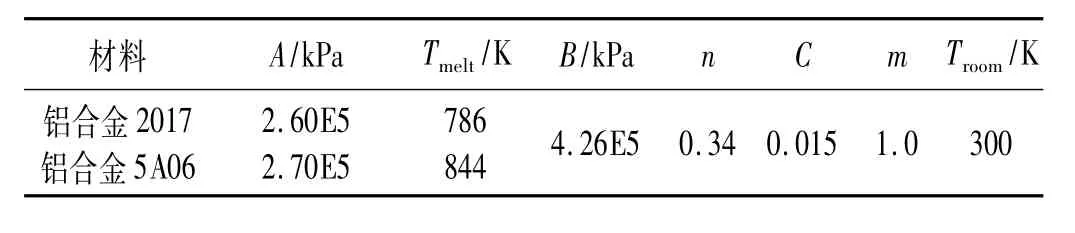
表2 Johnson-Cook强度模型参数Tab.2 Material parameters of Johnson-Cook strength model

实际材料不能承受任意大的拉伸应力，需要定义失效模型来描述材料的极限强度。超高速撞击引起的冲击波在弹丸和靶件中传播，通过在自由表面反射变成足够强的拉伸应力波，从而使被作用区域材料产生剥落破坏。根据实验及分析比较，失效模型采用最大拉应力准则，其参数见表3。随着计算的进行，在大变形区域会出现变形过大的网格，这样的畸变会导致较大误差甚至负体积，计算将无法进行下去。为防止这种现象，定义侵蚀准则，将满足其条件的畸变网格删除。根据实验及分析比较，采用最大瞬时应变准则，瞬时应变大于阈值的网格将被删除，其参数见表3。

表3 失效模型和侵蚀模型参数Tab.3 Material parameters of failure model and erosion model

1.2 超高速撞击数值模型

采用上述参数在AUTODYN中建立二维轴对称模型以模拟弹丸超高速撞击加筋板的工况，如图2所示，模型参数如表4所示。建模过程如下:首先，分别建立弹丸、筋体及基板三个部件;其次，划分网格(网格尺寸取0.2 mm)并将筋体及基板连接在一起;再次，对弹丸施加初始速度;最后在靶板正、反面距离撞击中心100 mm处分别设置观测点，用以记录其表面粒子法向运动速度，即声发射信号波形。由于在超高速撞击实验中，靶板自由悬挂在横梁上，由此引起的静应力远小于超高速撞击引起的动应力，故数值模型中不对靶板施加任何约束。

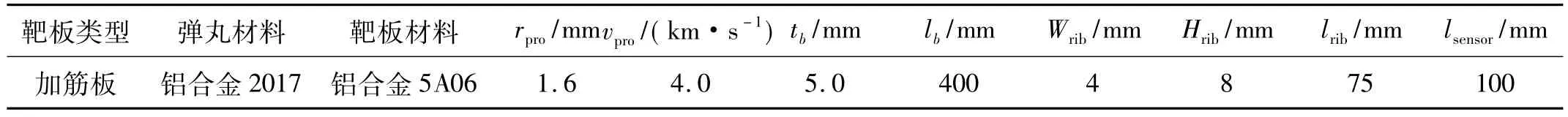
表4 弹丸撞击速度效应研究数值模拟工况Tab.4 Numerical cases of the study of the velocity effect of v pro

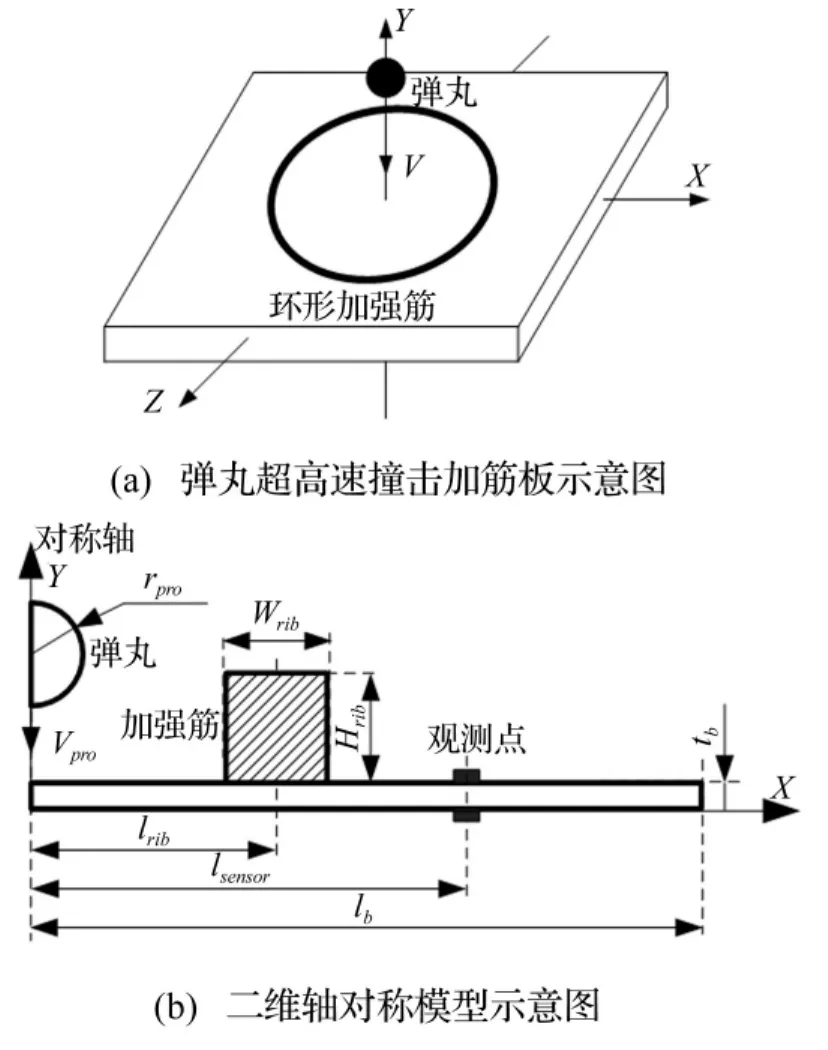
图2 弹丸超高速撞击加筋板二维轴对称模型Fig.2 2D FEM model of projectile impact stiffened plate

2 仿真结果与分析

2.1 超高速撞击声发射信号模态转换特性

通过仿真分别获得了靶板正面和背面距离撞击中心100 mm处的超高速撞击声发射信号。为避免边界反射波影响，截取50μs以内波形。为便于对其进行模态分析，采用如式(4)所示方法，分离声发射信号中的对称模态和非对称模态成分

式中，ΦS、ΦA分别为对称和非对称模态波形，Φf、Φb分别为靶板正面、背面声发射信号波形。其中

对ΦS、ΦA做小波变换，并将各模态板波群速度曲线叠加到小波谱图中。其中，不同模态成分的到达时刻如下式所示

式中，co(f)是原波速，ct(f)是模态转换后波速，To是保持原模态成分的到达时刻，Tt是模态转换成分的到达时刻，f指板波的频率，lrib、lsensor分别为凸起、换能器到撞击中心距离。叠加群速度曲线后的小波谱图如图3所示。观察图3(a)可发现，由S2模态转换而来的A1模态板波群速度曲线附近有能量分布。由此可知，S2模态板波经过加强筋后部分转换为A1模态板波。同理可知，S0、A0模态板波透射过筋体后分别部分转换为A0、S0模态板波，与文献［5－11］中的研究结果一致，分别见图3(a)、(b)。

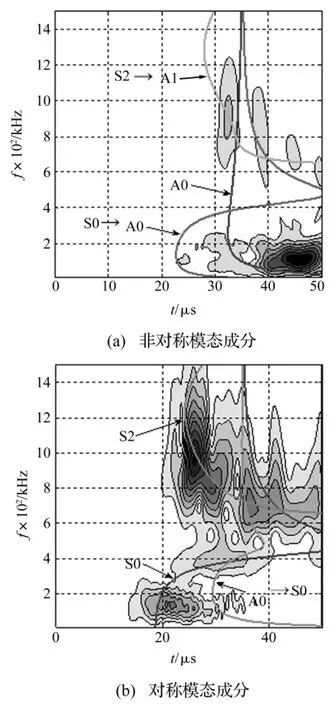
图3 加筋板中超高速撞击声发射信号小波谱图Fig.3 WT spectrum of signals in stiffened plate

2.2 A1阶板波模态转换特性

对于A1模态板波，为研究其透射过筋体时的模态转换现象，采用唐颀［13］给出的方法，利用LS-DYNA建立加筋板法向冲击力有限元模型，模拟法向冲击力载荷作用于5 mm厚圆形铝合金加筋板的工况以激发A1模态板波，如图4所示，靶板参数见表5。

计算采用显式动力学二维轴对称求解器，选用PLANE162轴对称类型单元，采用如表5所示材料参数。靶板中心具有Φ10 mm穿孔，网格密度5单元/mm。在圆孔内壁施加半正弦波形式的法向冲击载荷，其中法向冲击载荷表示为FN，载荷持续时间1μs。在靶板下表面距离中心600 mm处设置观测点，记录靶板表面粒子法向运动速度，即声发射信号波形。

图4 加筋板法向冲击载荷加载模型Fig.4 Simulation model of stiffened panel applied with impulse loads

表5 铝合金平板和加筋板法向冲击数值模拟工况Tab.5 Numerical cases of aluminum flat plate and stiffened plate

表6 5A06铝合金材料物理与弹性参数Tab.6 Physical and elastic parameters of 5A06 aluminum alloy

在法向冲击载荷作用下，靶板内产生A0、A1模态板波。对采集到的声发射信号进行小波变换，并叠加群速度曲线，结果如图4所示。由图可知，A1模态板波经过筋体后，部分转换为S0模态板波。

图5 透射波小波谱图Fig.5 WT spectrum of transmitted wave

3 结论

本文采用数值模拟手段，对超高速撞击声发射信号在靶板表面凸起处的模态转换现象，特别是其包含的S2阶板波的模态转换现象进行了研究。得到了如下结论:

(1)观察到S0阶板波经过筋体后会部分转换为A0模态板波，A0阶板波在经过筋体后会部分转换为S0模态板波。

(2)发现S2阶板波经过筋体后会部分转换为A1阶板波，而A1阶板波在筋体后会部分转换为S0阶板波。

［1］刘四清，刘静，师立勤，等.神舟五号的空间环境保障［J］.物理，2004，33(5):359－366.LIU Si-qing，LIU Jing，SHI Li-qin，et al.Space environment support for the SZ-5 spacecraft［J］.Physics，2004，33(5):359－366.

［2］ IADC WG3 members.Sensor systems to detect impacts on spacecraft ［R/OL］. http://www. iadc-online. org/Documents，2013.

［3］刘武刚，庞宝君，王志成，等.天基在轨空间碎片撞击监测技术的进展［J］.强度与环境，2008，35(1):57－64.LIU Wu-gang，PANG Bao-jun，WANG Zhi-cheng，et al.Technique advances about space debris in-situ impactsensing-system［J］.Structure ＆ Environment Engineering，2008，35(1):57－64.

［4］庞宝君，刘治东，张凯，等.空间碎片撞击在轨感知技术研究综述［J］.航天器环境工程，2010，27(4):412－419.PANG Bao-jun，LIU Zhi-dong，ZHANG Kai，et al.A review of studies of onboard sensor systems for space debris impact on spacecrafts［J］.Spacecraft Environment Engineering，2010，27(4):412－419.

［5］ Xu K L，Ta D，Su Z Q，et al.Transmission analysis of ultrasonic lamb mode conversion in a plate with partialthickness notch［J］.Ultrasonics，2014，54(1):395 －401.

［6 ］ Benmeddour F B，Grondel S， Assaad J A，et al.Experimental study of the A0 and S0 lamb waves interaction with symmetrical notches［J］.Ultrasonics，2009，49(2):202－205.

［7］ Fromme P，Rouge C.Directivity of guided ultrasonic wave scattering at notches and cracks［J］.Journal of Physics，2011，269(1):12－18.

［8］ Benmeddour F，Grondel S，Assaad J，et al.Study of the fundamental lamb modes interaction with asymmetrical discontinuities［J］.NDT ＆ E International，2008，41(1):330－340.

［9］ Reusser R S，Chimenti D E，Holland SD，et al.Plate wave transmission/reflection at geometric obstructions:Experiment［J］.Review of Progress in Quantitative Nondestructive Evaluation，2010，29:200－206.

［10］ Kim B，Roh Y.Simple expressions of the reflection and transmission coefficients of fundamental lamb waves by a rectangular notch［J］.Ultrasonics，2011，51(6):734 －744.

［11］ Reusser R S，Chimenti D E，Roberts R A，et al.Guided plate wave scattering at vertical stiffeners and its effect on source location［J］.Ultrasonics，2012，52(6):687 －693.

［12］刘武刚.基于声发射的空间碎片撞击在轨感知技术研究［D］.哈尔滨:哈尔滨工业大学，2008.

［13］唐颀.超高速撞击板波特性与声发射空间碎片在轨感知技术［D］.哈尔滨:哈尔滨工业大学，2008.

［14］ Wicklein M，Ryan S，White D M，et al.Hypervelocity impact on CFRP:testing，material modelling，and numerical simulation［J］.International Journal of Impact Engineering，2008，35(12):1861－1869.