大规模四面体网格并行生成方法

王小庆，金先龙

(1.上海交通大学 机械系统与振动国家重点实验室，上海 200240;2.上海交通大学 机械与动力工程学院，上海 200240)

网格生成是整个有限元计算的重要一环。在大型工程领域，比如抗震分析，抗爆炸冲击分析等，数值计算方法的应用越来越多，对求解精度的要求也越来越高，而这些对单元网格的需求规模也越来越大［1－4］，传统的串行网格生成限于时间及内存的限制［5－6］，很难满足超大规模数值计算的精度需要，而超级计算机的快速发展，也为网格生成的并行化提供了必需的硬件环境，并行网格划分已经成为网格生成领域的研究热点。

并行网格生成的研究方法主要集中在算法并行和问题并行两个方面。采用问题并行方式的研究较多，Laemmer等［7－8］提出了直接对几何体进行区域分解的二维三角形和三维四面体网格的并行生成方法，其对几何体的分区分别采用最大和最小极惯性轴递归对分的方法，提供了几何体划分的一种新思路，但是较难达到负载的均衡。Ivanov等［9－10］提出了对初始面网格分区，然后再并行生成体网格的方法。Ito等［11］提出了对初始体网格进行分区，然后利用前沿推进法进行并行网格生成的方法。在算法并行方面，Blelloch等［12－13］阐述了并行 Delaunay网格生成方法。Lhner等［14］对前沿推进法的并行化进行了研究。国内方面，关振群等［15］总结了有限元网格生成方法的研究进展，指出网格并行生成是未来有限元网格的发展方向。李水乡等［16］采用问题并行方式，实现了基于局域网的小规模有限元网格的并行生成。齐龙等［17］对GPU在并行网格生成中的应用进行了研究。王磊等［18］总结了各类Delaunay四面体网格并行生成算法的优缺点，并探讨了其发展趋势。

本文在上述研究基础上，提出了一种大规模非结构化四面体网格并行生成方法，采用问题并行的方式，直接读取CAD几何体文件，然后进行初始网格划分，并通过相对体积比及最优分区来控制初始网格数量，接着采用图划分理论对有限元网格进行区域分解，然后各个分区采用分裂法进行并行网格划分。利用初始体网格进行分区克服了利用初始面网格进行区域分解所带来的负载不均衡问题。提出的初始网格数量控制方法，最大限度的降低了此串行部分对并行效率的影响。针对分区间节点匹配的难题，提出了一种基于共享单元的边界处理方法，有效地解决了分区间边界协调的问题。最后通过算例证明了整个四面体并行生成方法可以获得良好的加速比和并行效率，所产生的网格具有较高质量可以直接用于后续并行计算。

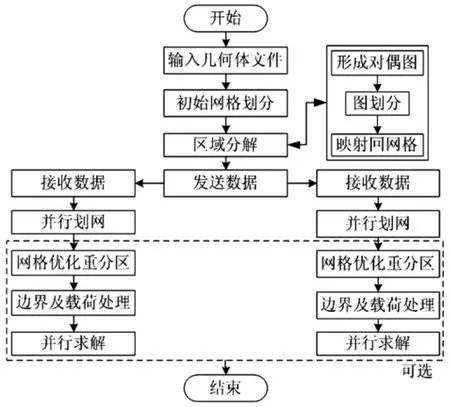
图1 并行网格生成流程图Fig.1 Flow Chart of parallel mesh generation

1 并行网格生成框架

此处所阐述的并行网格划分方法，作为后续自主开发的并行求解器的前处理器的核心算法，克服了传统串行网格划分时间及内存耗费的瓶颈［19］，程序采用C++和Fortran语言编写，利用MVAPICH并行库实现并行通信。本文采用问题并行方式，串行网格划分部分采用前沿推进法。

1.1 并行网格划分算法

如图1为并行网格划分的流程图。输入文件为通用CAD几何文件，采用前沿推进法［20］进行初始网格划分，并控制其产生合理的初始网格数;接着利用图论理论的图划分方法，进行区域分解，将各区域的数据发送到其余进程，然后采用分裂法进行并行网格生成。后续通过边界条件处理提交并行求解器进行求解计算，最后形成可视化后处理文件。在整个文件系统中，除了初始几何文件为单一文件传递外，其余文件均采用多文件传输处理，每个核负责处理自己的文件，并行多文件的利用，在很大程度上提高了程序的执行效率。

1.2 最优初始网格生成方法

初始网格划分的数量决定整个算法中串行部分的时间，划分数量过多，串行时间会过长，因而降低并行效率，划分数量过少，会导致模型失真，网格质量下降，同时所能进行的分区数也受到限制，影响并行规模的扩大。为合理解决此问题，此处采用双重约束对初始网格数量进行控制和优化。首先，保证初始网格的总体积和原几何体体积相对差值不大于5%，从而保证初始网格的几何贴切度，使有限元模型不失真，如式(1)为其约束条件。不同相对体积比初始网格效果如图2所示，可以看到对于单位球，其初始网格的体积和原几何体体积相对差值控制在4.8%时基本能保证模型不失真。其次，在保证最佳分区效果即保证分区均衡度的情况下，确定每个分区最少单元数，由于图剖分和图本身的拓扑有很大相关性，因此只能通过多次试验的方法确定其在一定分区数时对应的最佳单元数。

式中 a，b，c是共顶点的三条棱边的长度，α，β，γ 为相邻棱边组成的面角，ω为这三个面角和的一半。

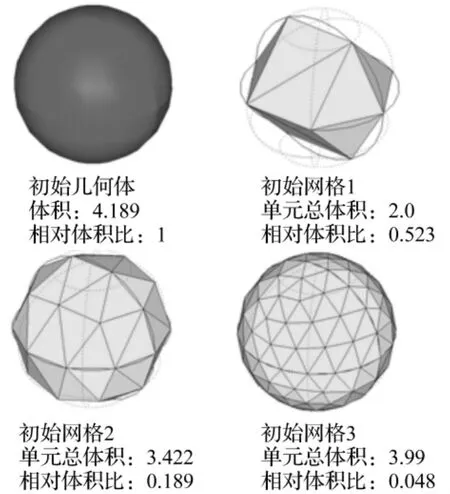
图2 不同体积比初始网格效果示意图Fig.2 Effect of different volume ration of initial mesh

1.3 区域分解技术

有限单元网格的区域分解，采用图论图划分方法。首先将单元信息转换为其对应的对偶图，然后将对偶图利用图论的方法进行区域分解，其过程分为粗化图阶段，图分区阶段及图还原阶段，最后再将分区结果映射还原为有限元网格的区域分解信息。图3所示为有限元网格与其相应对偶图的相互对应关系，每个有限元单元对应对偶图中的一个顶点，具有共享边(面)的单元，在对偶图中其相应的顶点之间，形成一条边。图中顶点和边上的数字代表权重，此处所有节点和边按照等权重处理，大小均置为1。

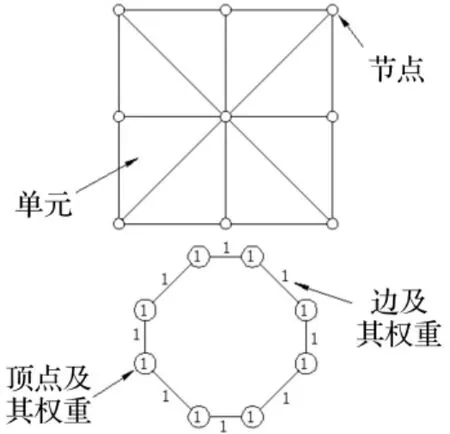
图3 有限元网格及其对偶图Fig.3 Finite element model and its dual graph

有限元模型转换形成的对偶图，利用CSR(compressed storage)格式进行存储。CSR格式在存储稀疏图领域有广泛应用。这种格式利用两个数组来表达图的邻接信息，第一个数组存储第i个顶点相邻顶点的开始和终了地址索引，第二个数组存储着每个顶点的邻接顶点，根据第一个数组中第i个顶点的索引可以在第二个数组中找到与其邻接的顶点。程序中具体实现采用metis的k路图划分方法［21］。基于图论理论的区域分解能够保证负载的均衡，提高并行效率。

1.4 基于分裂法的并行网格生成

初始网格进行区域分解后，由主进程发往各个进程，各从进程接收到数据后，利用分裂法对网格进行并行加密，实现网格的并行生成，直到满足网格数量及精度要求［20，22］。分裂法是在原单元各个边的中点生成新的节点，作为新增网格的顶点，然后分裂产生新的单元，一个三角形单元分裂为四个三角形单元，一个四面体单元分裂为8个四面体单元，其过程如图4所示。

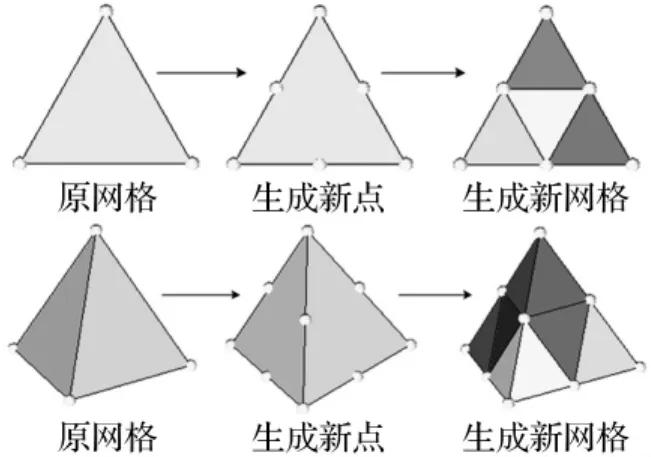
图4 二维、三维单元分裂示意图Fig.4 Schematic of 2D and 3D element split

采用分裂法很大程度上减少了各个分区之间的通信量，但是为了保证网格的整体性，各个分区边界上的节点应该保持一致的编号，否则无法进行后续计算或者网格的合并。为此，各个分区边界之间需要保持一定的通信，这里提出了一种基于共享单元的边界判定方法，首先根据对偶图区域分解结果，确定边界四面体单元;通过遍历所有边界单元的边，并在其所有共享进程之间进行通信，确定边界共享边;采用随机算法在共享进程间分配共享边;划分每个分区的边为内部边、属于自己的边界边、不属于自己的边界边三种类型，分别插入新的节点，并在相应边界之间交换节点信息;产生新的单元;进入下一个循环。基于共享单元的方法，借鉴了文献［10］基于共享节点的方法，同时克服了其无法处理图5情况的一个缺陷，图示该边的两个节点96和113被两个进程共享，采用基于共享节点的方法会判定其为边界边，但是事实上它是内部边;而采用基于单元的边界判定方法，通过对该边界单元四条边的遍历，及与其共享进程的通信，发现其共享进程Core1并没有该边，这样可以判定该边为内部边，而非边界边。基于共享单元分裂法的具体实现流程如图6所示。

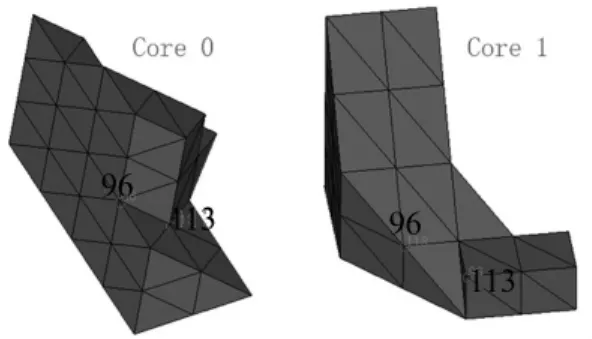
图5 特殊边界棱边示意图Fig.5 Schematic of special edge

2 算例分析

本节通过算例分析该算法的有效性和实用性。算例测试环境均为上海超级计算机中心“魔方”曙光5000A超级计算机，整机理论计算峰值为200 Tflops，具体计算区域为C区，该区由800个刀片式服务器组成，每个服务器包含四颗完全相同的AMD Barcelona 1.9 GHz四核处理器，每个刀片共享内存为64 G。所有服务器操作系统均为64位SuSE Linux Enterprise Server 10 SP2，通过LSF作业系统进行作业管理。

2.1 算例1

算例1选择在电力、冶金、石油、化工、水利等行业有广泛用途的滑动式马鞍支座，通过该算例验证算法的并行性能及可扩展性。首先通过图7直观的展现采用八个计算核心时，并行网格划分的具体实现过程，即包括几何体读入、初始网格划分、区域分解以及并行网格生成等。

图6 基于分裂法的并行网格生成流程图Fig.6 Flow chart of parallel mesh generation based on the split method

通过不同规模的网格及不同规模的核数，对算例进行分析，评估其时间性能，基于初始网格数量的控制方法，对于128核及其以下核数时，串行部分初始网格取877个，256核及其以上核数时，取初始网格取7 016个。如表1所示为不同规模不同核数时，网格划总分时间。可以看到，对于千万数量网格，可以在几秒内完成网格的划分;而对串行很难完成的亿以及十亿量级的网格划分，利用该并行网格生成方法可以很快完成，其中对将近二十亿的网格采用1024个处理核时，可以在大约0.28 min内完成网格划分。

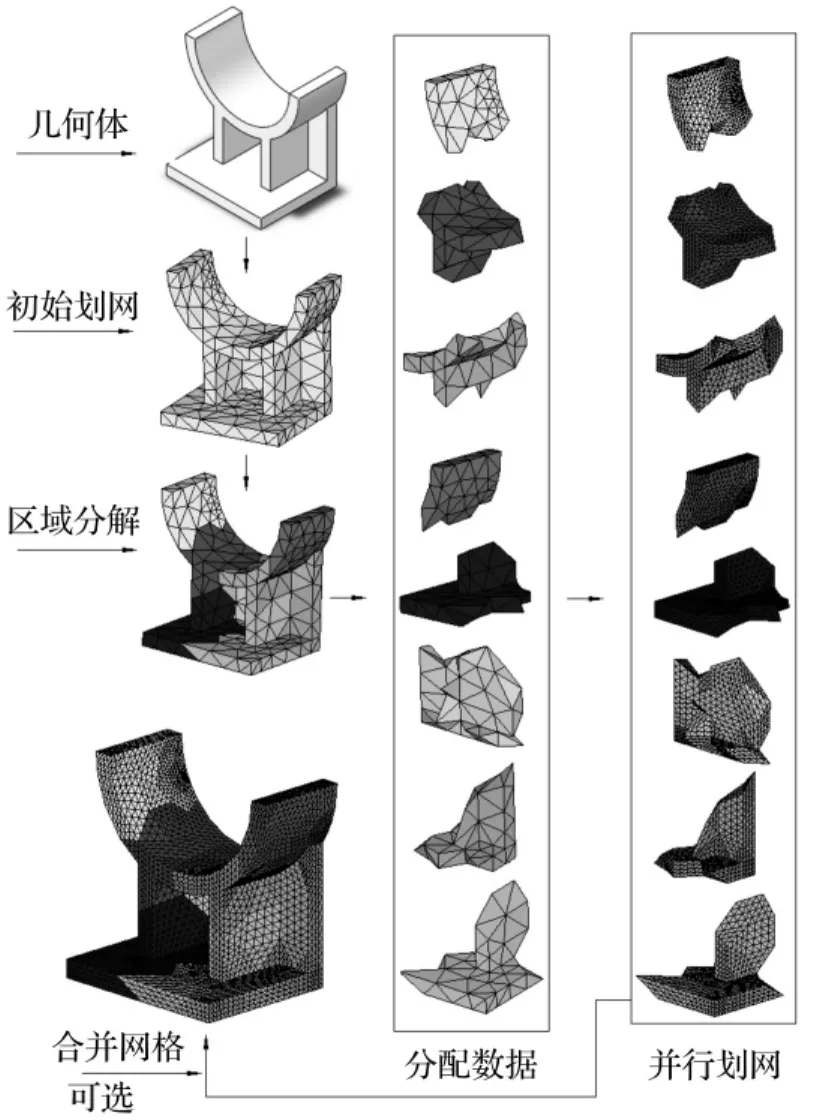
图7 八分区并行网格生成示意图Fig.7 Diagram of parallel mesh generation with 8 partitions

表1 生成不同数量网格总时间(s)Tab.1 Time of different amounts of element generation

并行算法的可扩展性是指随问题规模及计算资源的同比扩大，并行算法效率的稳定性。加速比是衡量可扩展性的常用方法。如图8为在问题规模固定为亿量级网格时，加速比随核数的变化。由图可以看到，在不考虑串行部分即初始网格划分和分区时间的情况下，该算法可以获得相当好的加速比。在考虑串行部分后，整体的加速比有所下降，128核、256核和512核均可以达到70%的并行效率，在1 024核情况下仍然达到大约56%的并行效率。

2.2 算例2

算例2选择具有实际工程应用背景的某核电站防浪堤抗震分析模型进行大规模非结构化网格的并行生成，主要考察生成网格的质量。整个模型长度2 km、宽度950 m、高度210 m。该算例采用1024个核进行网格的并行划分，总运行时间为100.3 s，最终的网格单元数2 750 414 848，节点数480 617 472，如图9所示为防浪堤抗震分析模型1024分区整体网格生成结果及局部网格详图。

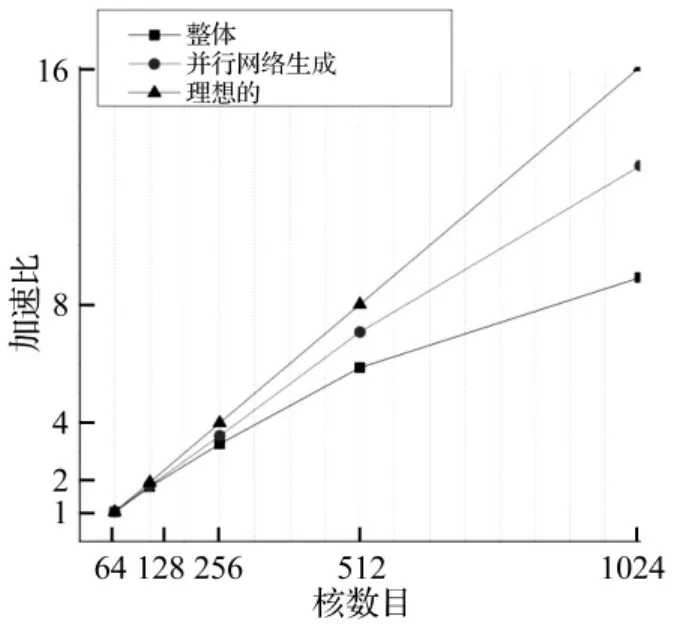
图8 并行网格生成加速比Fig.8 Speedup of parallel mesh generation

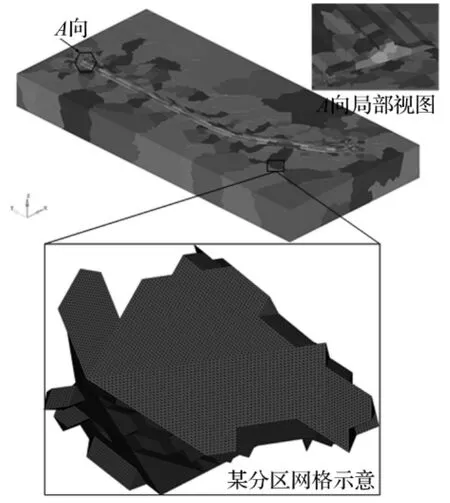
图9 防浪堤抗震模型1024分区并行网格划分结果Fig.9 Parallel mesh generation result of anti-seismic breakwater model with 1024 partitions

并行网格划分方法克服了串行划分方法的时间及内存的瓶颈，但是其网格质量必须满足后续串行或并行求解器的需要，为此，针对该算例分析其网格质量，这里将网格质量Q定义如式:

式中，VolIdeal=8r3/9，为与该四面体同一个外接球的理想四面体的体积，r为该四面体的外接球半径。VolActual为每个四面体的体积，通过式(2)可求得。理想的Q值为0，即该四面体为正四面体时，网格质量最高。如图10为防浪堤抗震模型网格质量的统计结果图，可以看到，Q值集中在0－0.3之间，和商业软件串行产生的网格质量分布情况类似，可以满足后续计算的需要。

图10 防浪堤抗震模型网格质量分布图Fig.10 Mesh quality distribution of anti-seismic breakwater model

3 结论

(1)所提出的非结构化四面体网格并行生成方法，克服了串行网格划分存在的瓶颈问题，通过算例证明了其高效性和所生成网格的实用性。

(2)提出的初始网格数量控制方法，减少了串行部分影响，有效地提高了并行效率;所述的基于共享单元的边界处理方式，有效地解决了各个分区之间边界节点的匹配，对类似边界之间的协调问题具有借鉴意义。

［1］邓荣兵，金先龙，陈峻.爆炸流场与玻璃幕墙动力响应的仿真计算方法［J］.振动与冲击，2011，30(3):14－17.DENG Rong-bing，JIN Xian-long，CHEN Jun.Numerical simulation method for blast flow and dynamic of glass curtain wall［J］.Journal of Vibration and Shock，2011，30(3):14 －17.

［2］ Zhou M，Xie T，Seol S，et al.Tools to support mesh adaptation on massively parallel computers［J］.Engineering with Computers，2012，28(3):287－301.

［3］Jou W.Comments on the feasibility of LES for commercial airplane wings［R］.AIAA －98－2801，1998.

［4］ Baum J D，Luo H，Lhner R.Numerical simulation of blast in the world trade center［C］.AIAA，Aerospace Sciences Meeting and Exhibit，33rd，Reno，NV.1995.

［5］马新武，王芳，赵国群.具有内部特征约束的四边形网格生成方法［J］.计算力学学报，2012，29(6):855－900.MA Xin-wu，WANGFang，ZHAO Guo-qun.An algorithm for quadrilateral mesh generation with internal feature constraints［J］.Chinese Journal of Computational Mechanics，2012，29(6):855－900.

［6］田素垒，张志毅，陈敏，等.四面体网格生成方法的研究与实现［J］.计算机工程与设计，2012，33(11):4416－4421.TIAN Su-lei，ZHANG Zhi-yi，CHEN Min，et al.Research and implementation of methods for tetrahedral mesh generation［J］.Computer Engineering and Design，2012，33(11):4416－4421.

［7］Laemmer I L.Parallel mesh generation［M］.Solving Irregularly Structured Problems in Parallel.Springer Berlin Heidelberg，1997:1 －12.

［8］ AndrH，Gluchshenko O N，Ivanov E G，et al.Automatic parallel generation of tetrahedral grids by using a domain decomposition approach［J］.Computational Mathematics and Mathematical Physics，2008，48(8):1367 －1375.

［9］ Ivanov E G， Andr H， Kudryavtsev A N. Domain decomposition approach for automatic parallel generation of tetrahedral grids［J］.Comput.Methods Appl.Math.，2006，6(2):178－193.

［10］ Ylmaz Y，zturan C，Tosun O，et al. Parallel mesh generation、migration and partitioning for the elmer application［R］.PRACE，2010:1－12.

［11］ Ito Y，Shih A M，Erukala A K，et al.Parallel unstructured mesh generation by an advancing front method［J］.Mathematics and Computers in Simulation，2007，75(5 －6):200－209.

［12］ Blelloch G E，Miller G L，Hardwick J C，et al.Design and implementation of a practical parallel Delaunay algorithm［J］.Algorithmica，1999，24(3－4):243－269.

［13］Chrisochoides N，Nave D.Parallel Delaunay mesh generation kernel［J］.International Journal for Numerical Methods in Engineering，2003，58(2):161－176.

［14］ Lhner R.A parallel advancing front grid generation scheme［J］. International Journal for Numerical Methods in Engineering，2001，51(6):663－678.

［15］关振群，宋超，顾元宪，等.有限元网格生成方法研究的新进展［J］.计算机辅助设计与图形学学报，2003，15(1):1－14.GUAN Zhen-qun， SONG Chao， GU Yuan-xian， et al.Recent advances of research on finite element mesh generation methods［J］.Journal of Computer-Aided Design ＆ Computer Graphics，2003，15(1):1 －14.

［16］李水乡，王云鹏，陈永强.基于局域网的有限元网格分布式并行生成［J］.计算机工程与设计，2005，26(12):3165－3166.LI Shui-xiang， WANG Yun-peng， CHEN Yong-qiang.Distributed parallel FEM mesh generation on LAN［J］.Computer Engineering and Design，2005，26(12):3165－3166.

［17］齐龙，肖素梅，刘云楚，等.基于GPU的并行非结构网格生成技术研究［J］.机械设计与制造，2013(2):184－186.QI Long，XIAO Su-mei，LIU Yun-chu，et al.Research on parallel unstructured mesh generation technology based on GPU［J］.Machinery Design ＆ Manufacturer，2013(2):184－186.

［18］王磊，聂玉峰，李义强.Delaunay四面体网格并行生成算法研究进展［J］.计算机辅助设计与图形学学报，2011，23(6):923－932.WANGLei，NIE Yu-feng，LI Yi-qiang，Advances of research on parallel Delaunay tetrahedral mesh generation ［J］.Journal of Computer-Aided Design ＆ Computer Graphics，2011，23(6):923 －932.

［19］ Larwood B G，Weatherill N P，Hassan O，et al.Domain decomposition approach for parallel unstructured meshgeneration［J］. International journal for numerical methods in engineering，2003，58(2):177－188.

［20］ Schberl J. NETGEN:an advancing front 2D/3D-mesh generator based on abstract rules［J］. Computing and visualization in science，1997，1(1):41－52.

［21］ Karypis G， Kumar V. Metis:a software package for partitioning unstructured graphs，partitioning meshes，and computing fill-reducing orderings of sparse matrices，version 5.1.0［M］.Minneapolis:Department of Computer Science and Engineering University of Minnesota，2013:26－30.

［22］Garatani K，Nakamura H，Okuda H，et al.GeoFEM:High performance parallel FEM for solid earth［C］.High-Performance Computing and Networking.Springer Berlin Heidelberg，1999:133－140.