KPCA和耦合隐马尔科夫模型在轴承故障诊断中的应用

刘 韬，陈 进，董广明

(1.昆明理工大学 机电工程学院，昆明 650500;2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

轴承作为旋转设备的关键部件，其故障是造成旋转机械故障的主要原因之一。因此，对轴承振动信号的状态监测与故障诊断一直是设备维护的重要研究领域［1］。当轴承故障发生时，首先需要从监测信号提取特征;然后对特征进行识别，判断故障类型［2］。

各种特征提取方法从不同角度描述了轴承状态的变化，通常总希望获取尽可能多的特征参数，但是特征维数的增加也会降低故障识别模型的效率。为了降低特征间的相关性，提高计算效率，很多特征约减方法诸如 PCA［3］、LPP［4］等已被引入轴承的故障诊断。但这些约减算法都属于线性映射算法，而轴承的振动信号具有非线性［5］，因此本文采用核主成分分析(Kernel Principal Component Analysis，KPCA)对提取的多维特征进行约减，在尽可能保留特征信息的基础上，降低特征样本的维数。隐马尔可夫模型(Hidden Markov Model，HMM)由于具有的双随机特性，因此被广泛用于轴承和齿轮等设备的故障诊断［6－7］。Brain等提出的耦合隐马尔可夫模型(Coupled Hidden Markov model，CHMM)［8］是对HMM的扩展，它描述了两个或多个相互关联的随机过程统计特性。本文在KPCA特征约减的基础上，利用CHMM对多通道数据的信息融合能力，研究了多链的CHMM在轴承故障诊断中的应用。最后通过实验验证了提出方法的可行性与有效性。

1 理论基础

1.1 核主成分分析

假设原始数据x共有l个样本，可以定义非线性映射 ，:xi→(xi)，i=1，…l，将数据从原始空间 Rn映射到高维空间F。然后对高维空间中的数据φ(x)进行主成分分析，假设(x)均值为零，即=0，则(x)的协方差矩阵可表示为:

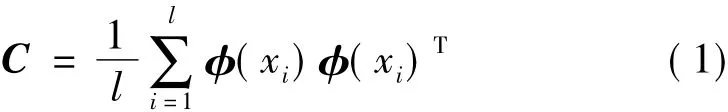
根据主成分分析原理，对矩阵C求解特征值和特征向量，可以得到下式:

式中，λ为C的特征值，V为C的特征向量。

将F空间中的每个样本与式(2)做内积，可以得到:

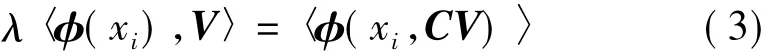
因为特征向量可以由数据集线性表示，所以有:

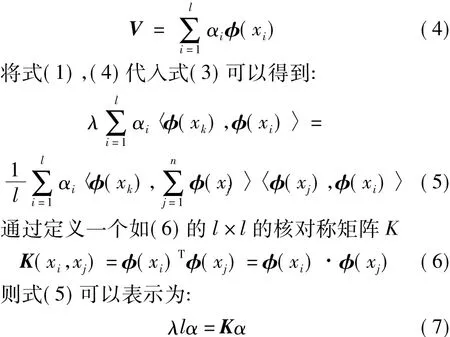
因此，通过求解(7)能得到K的特征值和对应的特征向量，然后就可以根据式(4)求得C的特征向量V，从而得到映射空间F的主元方向。

将K对角化，特征值为λ1≥λ2≥…≥λl，并将对应的特征向量［α1，α2，…αl］ 进行归一化，定义 p为主分量的数量。则有:

KPCA在输入空间仅依赖于输入样本空间的距离和内积，因此特征值及其约减只依赖于核函数及参数的选择。常用的核函数包括多项式核函数、多层感知器核函数和高斯径向基核函数等。由于支持向量对于不同的方法具有不敏感性［9］，即选用不同的核函数分类结果互相接近。因此，为简化计算，本文选用高斯径向基核函数(RBF):

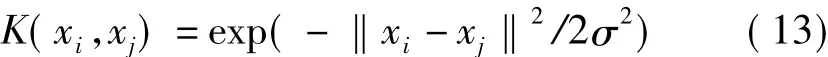
式中σ是宽度参数。在使用RBF进行KPCA分析时，较小的σ会引起过渡拟合，降低分类的泛化性能;而较大的σ会把核简化为一个常数函数，导致核函数变成平凡分类器。因此，本文引入了基于类内类间距离的核函数优选方法［10］，即寻找一个σ使得KPCA分类后的各个特征类的类内距离最小并且特征类间的距离最大［11］:

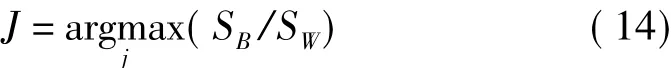
式中，SB是特征类的类间距离，SW各个特征类的类内距离。

1.2 耦合隐马尔耦合可夫模型

HMM是一个双重随机过程，即状态间的转移和各状态下的观测值都是随机的。假定状态序列和序列分别S和O，Rabiner［12］将一个HMM可以定义为:

其中，π=P(q1=Si)，1≤i≤N是初始状态概率向量，q1是t=1时刻，状态为Si的概率。A={aij］是状态转移概率矩阵，定义了t时刻状态为Si转移到t+1时刻状态为Sj的概率。B={bj(k)］是观测值概率矩阵，定义了t时刻，状态为Sj时观测值是vk的概率。

CHMM可以被认为是多个HMM通过在它们的状态序列间引入条件概率而得到的一种多链模型。图1描述了一个的双链的CHMM。

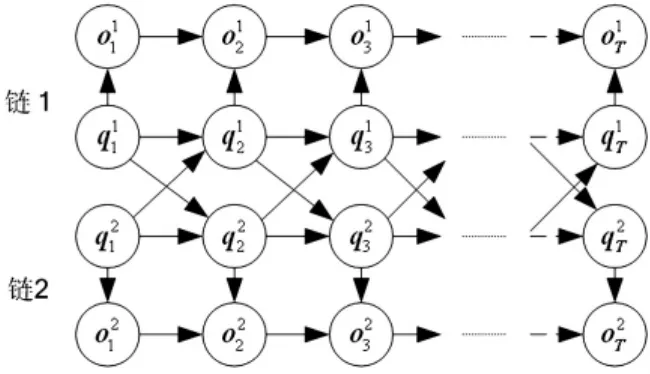
图1 双链的CHMMFig.1 A CHMM with two chains

CHMM同样可以被记为λ=(π，A，B)，但链c在t时刻的状态不但依赖于同链t－1时刻的状态，而且也与耦合链t－1时刻的状态有关，即状态转移概率是P(|qt－1)。但是链c的观测值仅与该链同一时刻的状态有关，因此有P(|qt－1)。如果CHMM的观测值序列和隐藏状态序列分别是{，，…，］和{，q，…，］，则式(15)中的各个参数可以定义为:

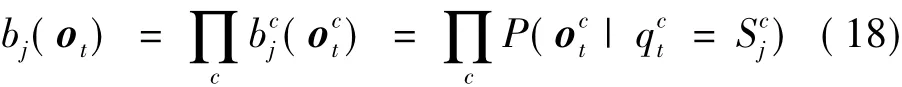
其中，c是链的数目，qt是时刻t时的状态。以双链CHMM 为例，c∈［1，2］，qt={，］。由于振动信号是连续的，通常使用高斯混合模型来拟合每条链在各个状态下的观测值概率密度函数:

式中是链c在状态的高斯元个数。和分别是第m个高斯元在状态的混合系数、均值向量和协方差矩阵。

1.3 基于核主成分分析和耦合隐马尔可夫模型的轴承故障诊断

基于KPCA特征约减和CHMM的轴承故障诊断过程如图2所示，具体步骤如下:

(1)对各个通道的训练和测试数据分别提取的多维特征。

(2)计算高斯核主元的最优参数并利用KPCA对训练和测试数据的特征维数进行约减，生成新的核主成分训练和测试样本。

(3)对训练数据不同状态下的样本分别训练CHMM并保存到模型库中。本文利用轴承在正常(NC)、内圈故障(IRF)、外圈故障(ORF)和滚动体故障(RBF)下的数据分别训练单个CHMM并组成模型库，即:λNC、λIRF、λORF和 λRBF。

(4)将测试样本送入CHMM模型库，分别计算样本在不同模型下的概率P(O|λi)，其中概率最大者就是测试样本的状态，即

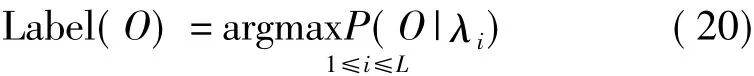
其中L=4，表示轴承有四种状态。

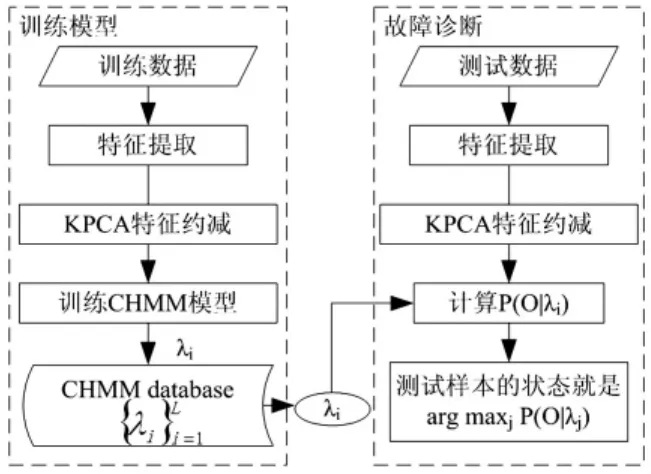
图2 基于KPCA和CHMM轴承故障诊断流程图Fig.2 Scheme of bearing fault diagnosis using KPCA and CHMM

2 实验分析

2.1 实验装置

为验证KPCA和CHMM在轴承故障诊断中的效果，本文利用图3所示的ZST－1轴承试验台分别采集了不同状态下的轴承振动信号。

试验轴承安装在转轴上，内圈随转轴转动，外圈被装夹装置固定，轴承在水平和垂直方向的振动信号分别被两个Kistler8791A250加速度传感器获取，然后通过NI 9234数据采集卡同步采集这两个通道的振动信号，采集程序使用NI LabVIEW编写。两个通道数据的采样频率都是25.6 kHz。实验轴承的型号是GB203深沟球轴承，具体参数如表1所示。试验模拟了轴承在正常状态和三种局部点蚀故障:内圈故障、外圈故障和滚动体故障的运行状况。其中，三种故障利用电火花在相应的表面上分别加工得到。试验一共采集了120组数据，每种状态各30组，每一组数据的时长是0.8 s。以通道一的一组数据为例，各种状态下轴承的时域波形如图4所示。

表1 GB203单列深沟球轴承的主要参数和工作条件Tab.1 Parameters and operating conditions of bearing GB203

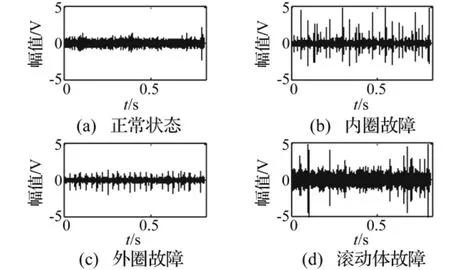
图4 轴承四种状态下的时域波形Fig.4 Time wave of bearing in four status

2.2 特征提取和约减

为了识别轴承故障，本文提取了11个时域和频域的特征并进行特征约减，包括:有效值、峰峰值、零峰值、歪度指标、峭度指标、峰值指标、裕度指标、脉冲指标、波形指标、谱总值和幅值谱熵。

以通道一的数据为例，将采集到的120组数据分为训练和测试数据。各状态下随机选择40%的数据作为该状态的训练数据，其余60%作为测试数据。对各组数据提取11个特征，可以得到训练特征矩阵和测试特征矩阵。然后利用KPCA对训练特征和测试特征进行约减，核函数宽度参数σ的选择如式(14)所述，以0.1为步长，对 σ∈［0.1，10］内的100 点进行优化计算，选取最优的=1.6。利用KPCA对训练特征和测试特征进行约减，为保证约减后的特征主元贡献率超过90%，保留了了前3阶主元进行分析。图5(a)和(b)分是训练特征和测试特征约减后的前3个主元的分布。可以看到，约减后的特征能够有效的辨识轴承4种不同状态下的样本，可以用于轴承故障的诊断。

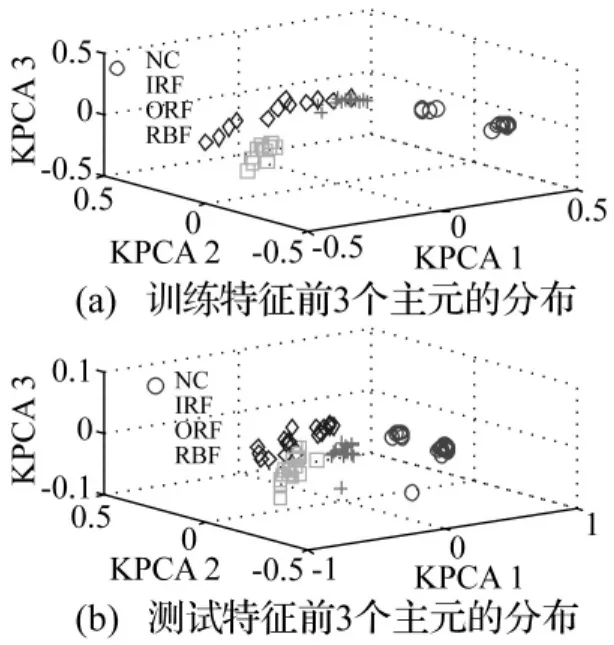
图5 KPCA特征约减结果Fig.5 The KPCA analysis of bearing data

2.3 诊断结果

利用KPCA约减后的训练特征分别训练4种状态下的CHMM模型，然后对测试特征进行诊断。训练和测试特征进行KPCA约减后的结果分别记为选取CHMM的参数如下:耦合链数目c=2，各链的状态数N=2，各状态下高斯元数目M=2。为了比较，本文也对利用PCA方法约减后的特征利用单链HMM模型进行诊断，其中 HMM的 N=2，M=2。HMM和CHMM的计算结果用对数似然率(Log-Likelihood)表示。不同状态的测试样本诊断的准确率如表2所示。为避免单次诊断可能导致的结果过于乐观或悲观，本文采用了5折交叉验证(Five-fold cross-validation)来估计诊断的准确率。每次随机选择各状态40%的样本训练模型，剩余60%的样本则作为测试样本计算诊断准确率，一共运行5次，取5次计算平均值作为最终诊断结果。任一状态的样本单次诊断的准确率可用式(21)进行计算:

其中一次诊断的效果如图6所示，图中a－d分别表示测试样本原本的状态分别是 NC，IRF，ORF和RBF。由图6(a)中可知，NC的测试样本(编号1－18)除编号3外，其余样本都是在模型λNC下得到了最大对数似然率输出，因此判断这些样本为正常状态，而编号3的样本则出现了误分。同理，IRF和ORF状态的样本全都能被正确诊断，RBF的样本则出现了两次误分(编号63和67)。图6(b)是利用通道一的KPCA特征和HMM诊断的结果，除了NC的测试样本出现了一次误分(编号3)，其余样本都能被正确诊断。图6(c)是利用两个通道的KPCA约减特征和CHMM的诊断结果，其中通道一和通道二优化后的宽度参数分别取=1.6 和=1.2。

图6 不同特征和模型的诊断结果Fig.6 Diagnosis results using different feature and models

表2 诊断结果比较Tab.2 Comparison of diagnosis results

表2给出了各种方法对轴承4种状态样本的诊断准确率。可以看到，KPCA的对特征约减的效果好于PCA，通过优化KPCA的宽度参数，可以获得比较理想的约减特征。由于轴承振动信号的非平稳性［13］，利用单通道数据和HMM进行分类时，KPCA特征分类的准确率除RBF样本略低于PCA外，对其余三种状态样本的诊断准确率都高于PCA特征，对全部样本诊断的平均诊断率也从94.2%提高到了96.9%。这也与KPCA特征约减后聚类效果优于PCA一致。同样使用KPCA特征进行训练和测试，CHMM诊断的准确率明显高于单通道的HMM(从96.9%提高到了98.9%)，这是由于双通道数据包含更丰富的信息，而CHMM能更准确的描述多通道数据间的统计特性。诊断准确率的大幅提高也证明了利用CHMM进行轴承故障诊断的有效性。

3 结论

由于KPCA可进行隐式的空间映射，省略了空间映射计算的复杂性，同时可进行非线性的复杂映射，解决了传统PCA只能线性映射，无法反应数据的非线性关系的缺陷。而CHMM的多链结构使得模型能有效的融合多通道数据信息，从而获得比单通道HMM获取更加准确和可靠的诊断结果。

本文提出一种基于KPCA和CHMM的轴承故障诊断方法，KPCA能有效的降低特征维度，增强特征的可分能力，而CHMM则充分利用轴承多通道数据的丰富信息。实验结果表明，所提出的方法比传统的PCA和HMM能更加有效的诊断轴承的故障。

［1］Lou X S，Loparo K A.Bearing fault diagnosis based on wavelet transform and fuzzy inference［J］.Mechanical Systems and Signal Processing，2004，18(5):1077－1095.

［2］Jiang QS，Jia M D，Hu JZ，et al.Machinery fault diagnosis using supervised manifold learning［J］.Mechanical Systems and Signal Processing，2009，23(7):2301－2311.

［3］Sun WX，Chen J，Li JQ.Decision tree and PCA-based fault diagnosis of rotating machinery［J］.Mechanical Systems and Signal Processing，2007，21(3):1300－1317.

［4］Yu J B.Bearing performance degradation assessment using locality preserving projections and Gaussian mixture models［J］.Mechanical Systems and Signal Processing，2011，25(7):2573－2588.

［5］Janjarasjitt S，Ocak H，Loparo K A.Bearing condition diagnosis and prognosis using applied nonlinear dynamical analysis of machine vibration signal［J］.Journal of Sound and Vibration，2008，317(1－2):112－126.

［6］张锐戈，谭永红.基于最优Morlet小波和隐马尔可夫模型的轴承故障诊断［J］.振动与冲击，2012，31(12):5－8.ZHANG Rui-ge，TAN Yong-hong.Fault diagnosis of rolling element bearings based on optimal morlet wavelet and hidden markov model［J］.Journal of Vibration and Shock，2012，31(12):5－8.

［7］滕红智，赵建民，贾希胜，等.基于CHMM的齿轮箱状态识别研究［J］.振动与冲击，2012，31(5):92－96.TENG Hong-zhi， ZHAO Jian-min， JIA Xi-sheng，et al.Gearbox state recognotion based on continuous hidden markov model［J］.Journal of Vibration and Shock，2012，31(5):92－96.

［8］Brand M，Oliver N，Pentland A.Coupled hidden Markov models for complex action recognition［C］//IEEE Computer Society Conference on Computer Vision and Pattern Recognition，San Juan，PR，USA，1997，994－999.

［9］ Bernhard Schlkopf， Alexander Smola， Müller K R.Nonlinear component analysis as a kernel Eigen value problem［J］.Neural Computation，1998:1299－1319.

［10］朱义.基于CHMM的设备性能退化评估方法研究［D］.上海:上海交通大学，2008.

［11］ Yang J，Frangi A F，Yang J Y，et al.KPCA plus LDA:a complete kernel Fisher discriminant framework for feature extraction and recognition［J］.Pattern Analysis and Machine Intelligence，IEEE Transactions on，2005，27(2):230－244.

［12］ Rabiner L R.A tutorial on hidden Markov models and selected applications in speech recognition［J］.Proceedings of the IEEE，1989，77(2):257－286.

［13］ Antoni J.Cyclic spectral analysis of rolling-element bearing signals:Facts and fictions［J］.Journal of Sound and Vibration，2007，304(3－5):497－529.