基于S变换谱阈值去噪的冲击特征提取方法

郭远晶，魏燕定，周晓军，唐 昉

(浙江大学 现代制造工程研究所，杭州 310027)

旋转机械设备出现某些故障时，如齿轮断齿、齿面磨损、轴承滚道或者滚动体表面金属剥落等，很大程度上会出现具有冲击特征的振动状态。但由于旋转机械设备传动系统的复杂性以及工作环境的多样性，各种激励源产生的振动信号相互耦合，导致故障源振动信号通常淹没在强背景信号与噪声中，比较难以识别。因此，若能成功提取所采集振动信号中的冲击特征，即可方便有效地对旋转机械设备相关故障进行诊断。

冲击特征信号是典型的非线性、非高斯信号。对于冲击特征的提取，国内外学者已经进行了一些相关的研究。LEE等［1－2］利用高阶统计量，如峭度、偏斜度等，对信号冲击成分具有高度敏感性的特点，提出以高阶统计量为优化目标函数的盲解卷积算法，从而提取冲击特征。李继猛等［3］提出了基于粒子群算法的多参数同步优化自适应单稳态随机共振方法，最优地检测出了原始信号中的冲击成分。章立军等［4］提出一种基于多尺度Top-Hat变换的形态非抽样小波分解方法，成功提取出了振动信号中的冲击特征。刘小峰等［5］采用Chirplet作为基函数对非平稳的瞬态冲击信号进行自适应分解，然后分别提出了时频滤波与模型逼近、Chirplet函数直接重构的冲击特征提纯方法。针对非高斯信号的处理，Simon等［6］首先提出基于高阶累积量和紧缩原理的时域迭代盲解卷积算法，王宇等［7］则在该算法的基础上，提出了盲解卷积和分层聚类的改进算法，并在机械声信号弱冲击成分提取中获得了较好的效果。杨富春等［8］利用信号的零时滞四阶累积量即峰态对非高斯信号非常敏感的特点，提出了滑动峰态算法的信号冲击特征提取方法。于明月等［9］利用所提出的双自适应小波局部极大模方法，有效地提取出了滚动轴承振动信号中的微弱冲击特征。

从噪声混合的信号中提纯冲击特征，国内外学者针对各自研究的对象信号提出了各种行之有效的方法，但最直接的方法依然是对信号进行降噪处理，以凸显冲击特征。因此，本文提出一种基于S变换谱阈值去噪的冲击特征提取方法。该方法以包含冲击特征的噪声混合信号为研究对象，先利用S变换获得其时频谱，然后根据谱系数的模值大小进行阈值去噪。去噪过程中，阈值函数分别采用了硬阈值函数和软阈值函数，最优阈值则利用步长迭代算法获取。最后利用S逆变换重构得到时域冲击特征。

1 S变换

1.1 连续S变换

S变换由 Stockwell在分析地球物理数据时提出［10－11］。对于给定的连续时间信号x(t)，其S变换定义为

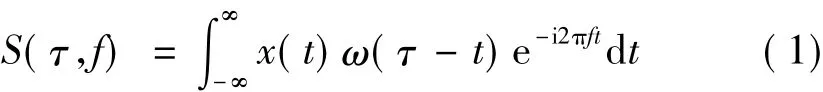
式中，S(τ，f)表示 x(t)的连续 S变换，t表示时间，f表示频率，参数τ控制着分析窗ω在t轴上位置。分析窗ω在时域定义为高斯窗

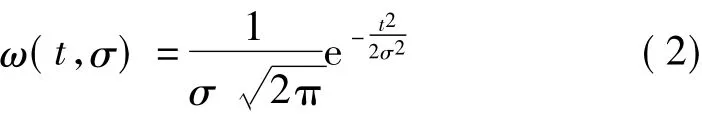
同时将控制窗宽的参数σ定义为信号频率的倒数，即

由此可见，S变换所用高斯窗的时宽与信号频率成反比关系，这使得S变换在信号低频段频率分辨率高，高频段时间分辨率高，也即S变换具有多分辨率特性，克服了短时Fourier分辨率固定的缺点，且对于频率突变且又暂态的信号冲击特征具有较高的敏感性。此外，S变换还满足线性叠加原理，不存在交叉项的干扰。假设噪声混合信号x(t)=s(t)+n(t)，n(t)为噪声信号，则有

S变换的以上特点使得其非常适合于处理与分析非平稳信号，尤其是包含冲击特征的信号。S变换谱表征的是信号局部频谱，因此，对信号x(t)的S变换谱沿时间轴积分，可以得到其Fourier谱，即

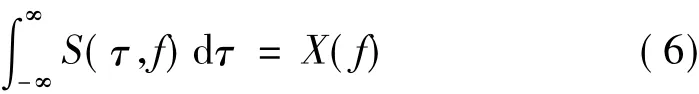
从而由S(τ，f)完全重构时域信号x(t)，即

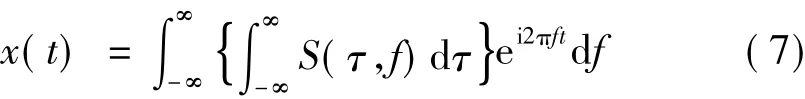
1.2 离散S变换

对于时域离散信号 x(k)(k=0，1，2，…，N －1)，其离散S变换的计算公式如下所示

其中，j，n=0，1，…，N － 1，X(n)为 X(k)的傅里叶变换。

离散S逆变换为

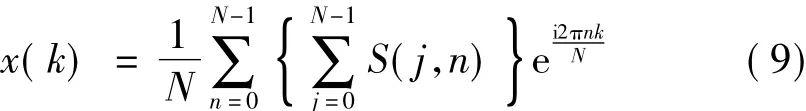
2 S变换谱阈值去噪

为了实现对冲击特征信号x(t)的S变换时频谱阈值去噪，以提纯其冲击特征，首先需要将x(t)进行S变换，得到其时频谱 S(j，n)(j，n=0，1，2，…，N －1)。由于S(j，n)为一个N×N的复数矩阵，对谱S(j，n)进行阈值去噪的方式便有两种:① 对谱系数的实部和虚部分别进行去噪;② 根据谱系数的模值大小进行去噪。考虑到前种方式会改变系数的相位，从而使S逆变换重构得到的时域信号产生附加噪声，所以本文采用后种方式。

为对S变换谱进行阈值去噪，首先需要获取最优阈值，针对于此，本文提出步长迭代算法。显然，最优阈值在［0，max{|S(j，n)|］］的 S 变换谱系数模值区间内。为了减少计算量，可以根据实际情况，定义最优阈值估计的一个较小的模值目标区间［α，β］·max{|S(j，n)|］，其中，［α，β］为模值系数区间，且 0≤α ＜ β≤1。最简单地，设定［α，β］=［0，1］，即 S 变换谱系数模值的全局区间;一般地，可以设定如［α，β］=［0.1，0.6］的子区间。因此，获取最优阈值的步长迭代算法具体步骤如下所述。

步骤1，将模值目标区间或者系数区间分成M个步长，则每个系数步长Δd=(β－α)/M，模值步长ΔD= Δd·max{|S(j，n)|］;阈值变量 δth初始化为 α·max{|S(j，n)|}。

步骤2，令阈值变量δth按模值步长ΔD增大，每增大一个模值步长，得到一个新阈值δnew。

步骤3，以δnew为阈值(包括初始值α·max{|S(j，n)|})进行S变换谱阈值去噪;去噪过程中所采用的阈值函数可以为硬阈值函数、软阈值函数或者其它的阈值函数;最后对去噪后的时频谱进行S逆变换，重构时域信号。

到这里，有必要探讨最优阈值的评价标准。

假设信号 x(k)(k=0，1，2，…，N －1)中真正的信号为s(k)，并包含有加法性噪声u(k)，则x(k)表示为x(k)=s(k)+u(k)。再令S变换谱经过阈值去噪后的S变换谱为S'(j，n)，那么经S逆变换重构得到的时域信号为

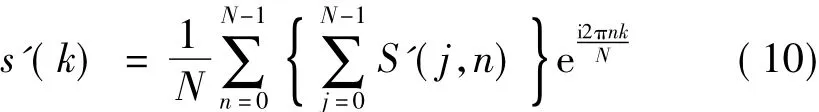
最优阈值δ*th去噪的目标是使s'(k)与真正信号s(k)的均方误差(Mean Squared Error)最小，也即使所谓的风险函数L2－RISK最小化，其定义为

但是，在处理实际信号时，s(k)是不可知的，L2－RISK无法计算，针对于此，本文提出一种改进风险函数，其定义为

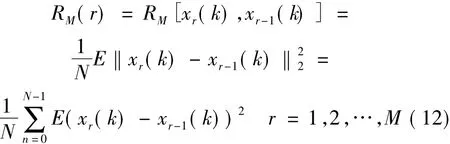
式中，r表示步数变量，xr(k)为阈值变量δth增加了r个模值步长，即 δth= α·max{|S［j，n］ |］ +r·ΔD 时，经过S变换谱阈值去噪后重构得到的时域信号。这样的话，RM(r)就定义为第r步阈值去噪得到的时域信号xr(k)与前一步阈值去噪得到的时域信号xr－1(k)的均方误差。

因此，在步骤3中，重构得到时域信号后，随之计算改进风险函数RM(r)。

步骤4，重复步骤2、3，直到阈值变量δth增加到β·max{|S［j，n］ |］，此时可以得到改进风险函数 RM(r)关于步数变量r或者阈值变量δth的关系曲线。

步骤5，对于硬阈值去噪，RM(r)曲线水平趋势段起始点所对应的阈值变量δth值即可认为是最优阈值。然而，此R(r)曲线一般为非平滑不规则曲线，需M要进一步根据M个RM(r)离散值进行多项式拟合，以得到RM(r)曲线的水平趋势。为使最优阈值δ*th的获取更为准确，拟合曲线的水平段范围应该可能宽，因而拟合次数也应该尽可能高，但其有限制，次数过高会使拟合曲线不能明显呈现甚至没有水平段。最终以拟合趋势曲线水平段起始点所对应的阈值变量δth值作为最优阈值。

对于软阈值去噪，RM(r)曲线通常为衰减的平滑曲线，当RM(r)曲线衰减至呈较为平缓趋势、且其值已经足够小时，其上某一点所对应的阈值变量δth值即可认为是最优阈值。如果按此方式不便判断，则进一步定义RM(r)差分谱

当d RM(r)曲线衰减至呈水平趋势、且其值已经足够小时，其上某一点所对应的阈值变量δth值即可认为是最优阈值δ*th。

需要说明的是，由改进风险函数RM(r)或者其差分谱d RM(r)确定最优阈值δ*th的方法带有一定的主观性与试探性，但其有足够的准确性，并不影响其实用性。

最后，利用步长迭代算法中估计的最优阈值δ*th重新对信号x(t)进行S变换谱阈值去噪，再利用S逆变换重构时域信号，得到信号x(t)中的冲击特征。

3 仿真研究

为验证S变换谱阈值去噪方法对于噪声混合信号冲击特征提取的有效性，构造仿真信号x(t)进行试验。信号x(t)中的冲击成分p(t)由下面指数衰减模型生成，

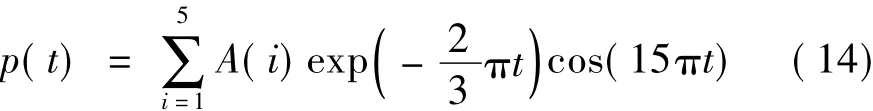
其中，信号幅值序列 A(i)(i=1，2，…，5)，为均值 μ=2，标准差σ=0.3的高斯随机序列，冲击分量p(t)如图1所示。冲击分量叠加高斯白噪声，得到信噪比为0的仿真信号x(t)，如图2所示。

图1 冲击分量p(t)Fig.1 Impact component p(t)

对x(t)进行S变换，得到其时频谱系数的最大模值 max{|S(j，n)|］=1.685 3。在运用步长迭代算法的过程中，取模值系数区间［α，β］=［0.1，0.6］，将区间分成M=100个步长。去噪过程中分别采用硬阈值函数和软阈值函数，其中硬阈值函数的表达式为

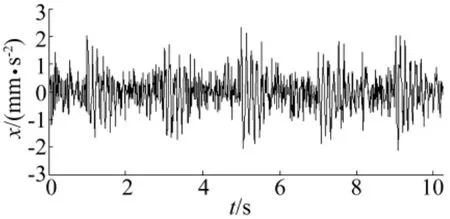
图2 仿真信号x(t)Fig.2 Simulated signal x(t)

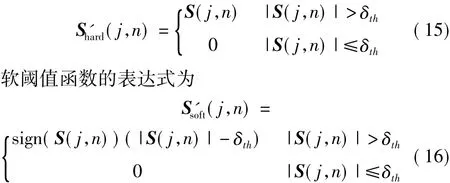
对于硬阈值去噪，RM(r)关于步数变量r的关系曲线及其15次多项式拟合曲线如图3所示。

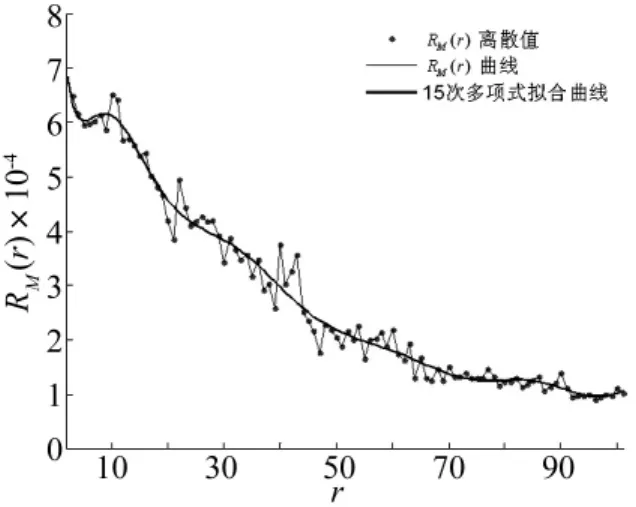
图3 仿真信号x(t)经硬阈值去噪得到的改进风险函数RM(r)曲线及其15次多项式拟合曲线Fig.3 Modified risk function RM(r)curve obtained from the simulated signal x(t)by hard threshold denoising and its 15th degree polynomial curve

可以看出，当阈值变量δth增加的步数r=75，即δth= α·max{|S(j，n)|］+r·ΔD=0.800 5 时，RM(r)曲线出现水平趋势段。因此，估计的最优阈值=0.800 5，然后以此最优阈值对信号x(t)重新进行S变换谱硬阈值去噪，最后利用S逆变换重构得到时域冲击特征p'(t)，如图4所示。

对于软阈值去噪，RM(r)关于步数变量r的关系曲线如图5所示。

可以认为，当阈值阈值变量δth增加的模值步数r=45，即 δth= α·max{|S［j，n］|］+r·ΔD=0.547 7 时，RM(r)曲线趋于水平。进一步地，从图6所示的差分谱d RM(r)曲线可以看出，当r=45时，差分谱d RM(r)曲线衰减呈水平趋势，且其值就已经足够小。因此，估计的最优阈值=0.547 7，然后以此最优阈值对信号x(t)重新进行S变换谱软阈值去噪，最后利用S逆变换重构得到时域冲击特征p'(t)，如图7所示。

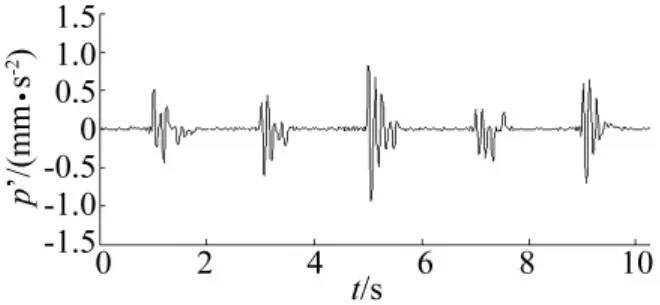
图4 仿真信号x(t)经硬阈值去噪得到的时域冲击特征Fig.4 Time-domain impact feature obtained from the simulated signal x(t)by hard threshold denoising

图5 仿真信号x(t)经软阈值去噪得到的改进风险函数RM(r)曲线Fig.5 Modified risk function RM(r)curve obtained from the simulated signal x(t)by soft threshold denoising

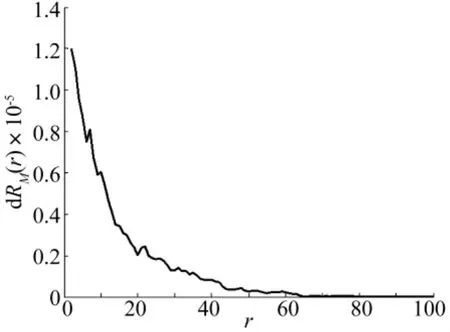
图6 仿真信号x(t)改进风险函数RM(r)的差分谱d RM(r)曲线Fig.6 Difference spectrum d RM(r)curve obtained from the modified risk function RM(r)of the simulated signal x(t)

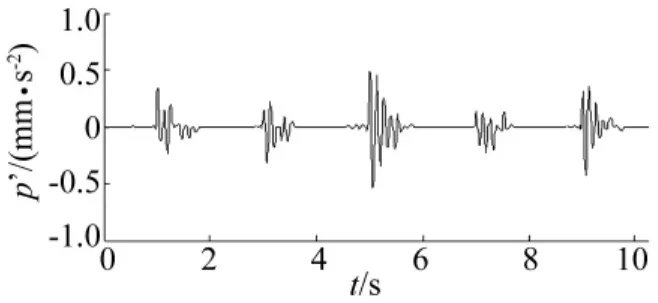
图7 仿真信号x(t)经软阈值去噪得到的时域冲击特征Fig.7 Time-domain impact feature obtained from the simulated signal x(t)by soft threshold denoising

本次仿真试验中，S变换谱硬阈值去噪和软阈值去噪所达到的效果基本一样，均能够从噪声混合信号x(t)中提纯时域冲击特征。对比图1、图4和图7，可以看出，虽然所得到的冲击特征幅值已经失真，这主要是由S变换中的高斯窗函数以及阈值函数所决定的，但成功提取出了作为最重要信息的冲击特征出现周期，进而可以计算冲击特征频率，这验证了所提出的S变换谱阈值去噪方法对于信号冲击特征提取的有效性。

4 轴承故障信号实例分析

为进一步验证S变换谱阈值去噪方法在实际故障振动信号中提取冲击特征的有效性与实用性，下面采用美国Case Western Reserve University电气工程实验室中的相关轴承数据进行试验［12］。试验轴承为试验台驱动端的SKF 6205－2RS轴承。在试验轴承内滚道上用电火花加工出直径为0.177 8 mm，深为0.279 4 mm的凹坑，以模拟轴承内圈单点故障。驱动电机功率2.2 kW，试验转速1 730 r/min。理论计算该轴承内圈故障特征频率为156 Hz。采样频率为12 kHz，采样数据长度为2 048。显然，该轴承在运行过程中，会产生具有冲击特征的振动信号，且冲击特征出现频率与为轴承内圈故障特征频率一致。待分析的轴承故障振动信号如图8所示，现采用S变换谱阈值去噪方法将其中的冲击特征提取出来。

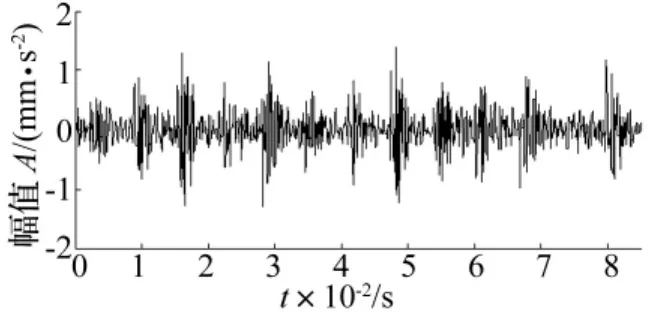
图8 轴承故障振动信号Fig.8 Bearing fault vibration signal

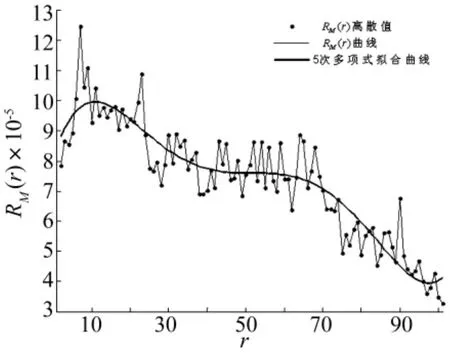
图9 轴承故障振动信号经硬阈值去噪得到的改进风险函数RM(r)曲线及其5次多项式拟合曲线Fig.9 Modified risk function RM(r)curve obtained from the bearing fault vibration signal by hard threshold denoising and its 5th degree polynomial curve

图10 轴承故障振动信号经硬阈值去噪得到的时域冲击特征Fig.10 Time-domain impact feature obtained from the bearing fault vibration signal by hard threshold denoising

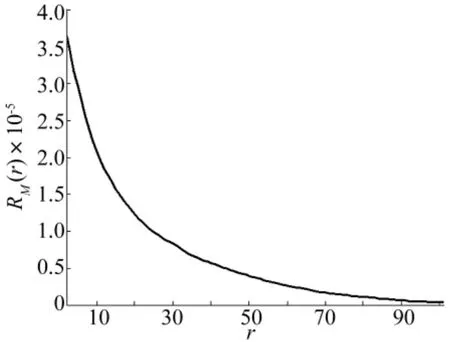
图11 轴承故障振动信号经软阈值去噪得到的改进风险函数RM(r)曲线Fig.11 Modified risk function RM(r)curve obtained from the bearing fault vibration signal by soft threshold denoising

对该轴承故障振动信号进行S变换，得到其时频谱系数的最大模值 max{|S(j，n)|］=0.635 8。在运用步长迭代算法的过程中，取模值系数区间［α，β］=［0.1，0.7］，并将区间分成 M=100 个步长。去噪过程中同样分别采用硬阈值函数和软阈值函数。

对于硬阈值去噪，RM(r)关于步数变量r的关系曲线及其5次多项式拟合曲线如图9所示。

不难看出，当阈值阈值变量δth增加的模值步长数r=45，即 δth= α·max{|S［j，n］|］+r·ΔD=0.765 9时，RM(r)曲线出现水平趋势段。因此，估计的最优阈值=0.235 3，然后以此最优阈值对轴承故障振动信号重新进行S变换谱硬阈值去噪，最后利用S逆变换重构得到轴承故障振动信号中的冲击特征，如图10所示。

对于软阈值去噪，RM(r)关于步长数M的关系曲线如图11所示。

可以认为，当阈值阈值变量δth增加的模值步长数r=26，即 δth= α·max{|S［j，n］|］+M·ΔD=0.1628时，RM(r)曲线衰减趋势较为平缓。进一步地，从图12所示的差分谱d RM(r)曲线看出，当M=26时，差分谱d RM(r)曲线趋于水平，且其值已经很小。因此，估计的最优阈值=0.162 8，然后以此最优阈值对轴承故障振动信号重新进行S变换谱软阈值去噪，最后利用S逆变换重构得到时域冲击特征，如图13所示。

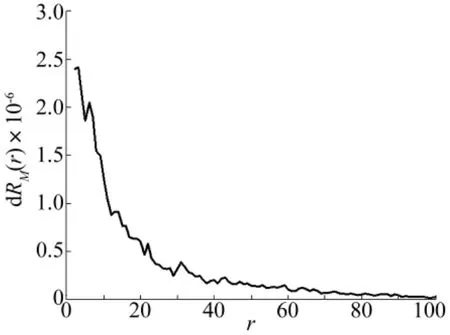
图12 轴承故障振动信号改进风险函数RM(r)的差分谱d RM(r)曲线Fig.12 Difference spectrum d RM(r)curve obtained from the modified risk function RM(r)of the bearing fault vibration signal

图13 轴承故障振动信号经软阈值去噪得到的时域冲击特征Fig.13 Time-domain impact feature obtained from the bearing fault vibration signal by soft threshold denoising

轴承故障振动信号的处理结果显示，S变换谱硬阈值去噪和软阈值去噪这两种方法均能够成功地从轴承故障振动信号中提取出较为纯粹的时域冲击特征。从图10和图13中，可以明显看出冲击特征出现的周期为 Δt=0.006 45 s，对应的频率为 155 Hz，这与该滚动轴承内圈的故障特征频率156 Hz基本一致，从而可以准确作出故障诊断结论。

作为比较，现对轴承故障振动信号分别进行小波硬阈值去噪与软阈值去噪。

小波硬阈值去噪的阈值采用S变换谱硬阈值去噪所用的最优阈值=0.235 3，这样得到轴承故障振动信号的小波硬阈值去噪结果如图14所示。

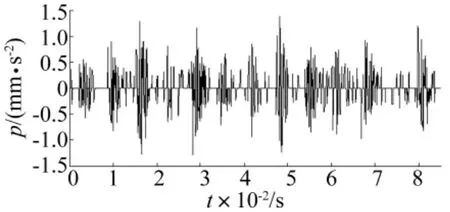
图14 轴承故障振动信号经小波硬阈值去噪得到的时域冲击特征Fig.14 Time-domain impact feature obtained from the bearing fault vibration signal by wavelet hard threshold denoising

小波软阈值去噪的阈值采用S变换谱软阈值去噪所用的最优阈值=0.162 8，这样得到轴承故障振动信号的小波软阈值去噪结果如图15所示。

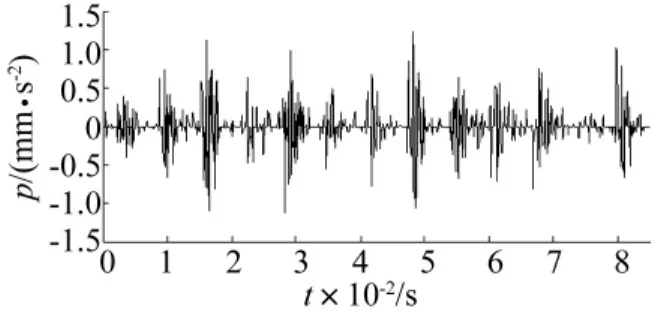
图15 轴承故障振动信号经小波软阈值去噪得到的时域冲击特征Fig.15 Time-domain impact feature obtained from the bearing faultvibration signal by wavelet soft threshold denoising

通过比较可以明显看出，利用步长迭代算法估计的最优阈值，S变换谱硬、软阈值去噪方法所提取出的轴承故障振动信号时域冲击特征更为纯粹，其中的各个冲击特征之间没有噪声成分的干扰。因此，针对含噪信号时域冲击特征的提取，相比于小波硬、软阈值去噪，S变换谱阈值去噪方法更具有优越性。

5 结论

(1)S变换具有多分辨率特性，满足线性叠加原理，且对于暂态的信号冲击特征具有较高的敏感性，非常适合于处理与分析非平稳信号，尤其是包含冲击特征的信号。

(2)利用所提出的改进风险函数RM(r)或者其差分谱d RM(r)，步长迭代算法能够准确有效地从0到S变换谱系数最大模值的区间内估计S变换谱阈值去噪所需的最优阈值，虽然的获取带有一定的主观性，但并不影响其实用性。

(3)S变换谱阈值去噪方法可以成功地从噪声混合信号中提取出较为纯粹的时域冲击特征，且相比于小波硬、软阈值去噪，更具有优越性。最终根据所获取的冲击特征频率，可以有效方便地实现滚动轴承相关故障的诊断。

［1］Lee J Y，Nandi A K.Blind deconvolution of impacting signals using higher-order statistics［J］.Mechanical Systems and Signal Processing，1998，12(2):357－371.

［2］ Lee J Y，Nandi A K.Extraction of impacting signals using blind deconvolution ［J］.Journal of Sound and Vibration，2000，232(5):945－962.

［3］李继猛，陈雪峰，何正嘉.采用粒子群算法的冲击信号自适应单稳态随机共振检测方法［J］.机械工程学报，2011，47(21):58－63.LI Ji-meng， CHEN Xue-feng， HE Zheng-jia. Adaptive monostable stochastic resonance based on PSO with application in impact signal detection ［J］.Journal of Mechanical Engineering，2011，47(21):58 －63.

［4］章立军，阳建宏，徐金梧，等.形态非抽样小波及其在冲击信号特征提取中的应用［J］.振动与冲击，2007，26(10):56－59.ZHANG Li-jun， YANG Jian-hong， XU Jin-Wu， et al.Morphological undecimated wavelet and its application to feature extraction of impulsive signal［J］. Journal of Vibration and Shock，2007，26(10):56－59.

［5］刘小峰，柏林，秦树人.基于自适应时频分解的瞬态冲击信号提纯［J］.机械工程学报，2008，44(11):166－170.LIU Xiao-feng，BO Lin，QIN Shu-ren.Transient impulse signal extraction based on self-adaptive time-frequency decomposition［J］. Chinese Journal of Mechanical Engineering，2008，44(11):166 －170.

［6］ Simon C，Loubaton P H，Jutten C，et al.Separation of a class of convolutive mixtures:a contrast function approach［J］.Signal Processing，2001，81(4):883 －887.

［7］王宇，伍星，迟毅林，等.基于盲解卷积和聚类的机械弱冲击声信号提取［J］.振动工程学报，2009，22(6):620－624.WANG Yu，WU Xing，CHI Yi-lin，et al.Weak transient impulse signal extraction based on blind deconvolution and cluster in acoustical machine diagnosis［J］.Journal of Vibration Engineering，2009，22(6):620 －624.

［8］杨富春，周晓军，张志刚.基于滑动峰态算法的信号弱冲击特征提取及应用［J］.振动与冲击，2009，28(4):103－105.YANG Fu-chun，ZHOU Xiao-jun，ZHANG Zhi-gang.A new method for extracting weak impulse characteristic based on a sliding kurtosis algorithm ［J］.Journal of Vibration and Shock，2009，28(4):103－105.

［9］于明月，陈果.双自适应小波局部极大模方法及其在信号特征提取中的应用［J］.振动与冲击，2013，32(1):53－59.YU Ming-yue，CHEN Guo.Double adaptive wavelet partial maximum modulus method and its application in feature extraction of impulse signals［J］.Journal of Vibration and Shock，2013，32(1):53－59.

［10］Stockwell R G，Mansinha L，Lowe R P.Localization of the Complex Spectrum:The STransform［J］.IEEE Transactions on Signal Processing，1996，44(4):998 －1001.

［11］ Stockwell R G.Why use the S-transform? ［J］.Fields Institute Communications，2007，52:279－309.

［12］ Welcome to the Case Western Reserve University Bearing Data Center Website［EB/OL］.http://csegroups.case.edu/bearing dataconter/home