基于EEMD分解的输电塔阻尼特性识别

沈国辉， 项国通， 邢月龙， 郭 勇， 孙炳楠

(1.浙江大学 土木工程学系，杭州 310058;2.华南理工大学 建筑设计研究院，广州 510640;3.浙江省电力设计院，杭州 310007)

风荷载是输电塔的主要控制荷载，准确合理地计算输电塔在风荷载作用下的动力响应具有重要意义。输电塔的风振响应具有随机、非平稳和非线性等特征，其阻尼特性的识别一直是个难题。通常根据结构动力响应的时间历程来评估阻尼，阻尼的识别方法可以分成两大类，即谱方法和时间序列法。用于阻尼识别的输电塔响应时程通常来源于现场实测和气弹模型风洞试验。

汪江等［1－3］实测了某输电塔的加速度响应，利用半功率谱带宽法识别结构的各阶模态阻尼。但有研究表明［4］，半功率谱带宽法由于受到信号处理中的采样频率、频率分辨率、采样长度等因素影响，识别的阻尼比数据离散较大且不稳定。李正良等［5－8］基于输电塔气弹模型风洞试验的加速度测试结果，利用经验模态分解法(Empirical Mode Decomposition，EMD)获得本征模态函数(Intrinsic Mode Function，IMF)，结合随机减量法和Hilbert变换识别输电塔气弹模型的整体阻尼和气动阻尼。EMD方法在处理非线性、非平稳时间序列表现出一定的优势，但采用EMD方法时可能会存在一定程度的模态混叠现象［9－10］。鉴于EMD方法的不足，Wu等［11］在EMD方法基础上添加了噪声辅助分析，提出了集合经验模态分解法(Ensemble Empirical Mode Decomposition，EEMD)。目前利用EEMD方法进行结构物(包括输电塔)阻尼特性识别的研究几乎没有。

本文以一典型的输电塔为例，分6个风速和7个风向角在B类地貌下进行气弹模型测振风洞试验，分别采用EMD和EEMD方法分解风洞试验获得的加速度时程，对比两种分解方法得到的IMF以分析EEMD方法的优越性，然后运用EEMD方法、改进的随机减量法和Hilbert变换法识别输电塔气弹模型在各风速和风向角下的频率和阻尼，并探讨输电塔顺线向和横线向阻尼随风速和风向的变化特征，为结构物的阻尼识别方法和输电塔的振动特性研究提供参考。

1 阻尼的识别原理和方法

1.1 经验模态分解法(EMD)

经验模态分解法基于信号局部特征的时间尺度，从信号中提取出本征振动模态，采用本征模态函数(IMF)来反应原信号。IMF须满足如下两个条件:①在信号的整个持续时间内，零交点的数目与极值点的数目必须相等或至多相差一个;②在任意时刻，由局部极大值点定义的上包络线和由局部极小值点定义的下包络线之间的平均值为零。

Huang等［9］发展了一种将任意信号分解成本征模态函数(IMF)分量的方法，即经验模态分解法。与其他信号处理方法相比，EMD方法是直接的、后验的、自适应的，其分解基是源自于原始信号。该方法的实质是通过特征时间尺度来识别信号中所固有的本征振动模态。EMD分解的核心是筛分过程，通过筛分得到IMF。筛分的处理过程为:将信号波形中所有局部极大值点和局部极小值点识别出来，用三次样条曲线将所有局部极大点(极小值)连接起来构成原始波形的上(下)包络线，求出上下包络的平均值，将原始信号减去平均值即为一次筛分过程。

EMD存在模态混叠问题，其原因为信号的间断。间断使得时域空间的某些尺度丢失，不仅引起了严重的模态混叠，而且使单独的IMF分量缺乏物理意义。为了减轻EMD方法的模态混叠，Huang等［12］曾提出了间断测试，但模态混叠问题并没有得到非常好的解决。另外，EMD方法边界问题的处理也是一大难点，目前工程上常用的EMD边界处理方法有镜像法、神经网络预测、多项式外延方法等，但各自都有其局限性。

1.2 集合经验模态分解法(EEMD)

集合经验模态分解(EEMD)［11］把一个全体测试的均值定义为真实的本征模态函数分量，其中每个测试都包含了信号和有限幅值的白噪声，使用该方法能够明确地分离出各个尺度的信号，不用任何预先的主观标准选择。

EEMD的原理为:当信号加入均匀分布的白噪声背景时，不同尺度的信号区域将自动映射到与背景白噪声建立的相关的、适当的尺度上;每次独立的试验可能会产生信噪比很大的结果，但足够多的试验全体均值将会消除噪声;全体的均值将会被认为是真正的结果，当试验的个数足够多时，试验全体均值中唯一存在的部分是信号本身。

EEMD方法的实现过程如下［11］:

(1)在目标数据上加入白噪声序列;

(2)将加入白噪声后的序列分解为IMF;

(3)每次加入不同的白噪声序列，重复步骤1、步骤2;

(4)把每次分解得到的相应IMF的均值作为最终的结果。

1.3 改进的随机减量法(RDT)

随机减量法(Random Decrement Technique，RDT)利用随机信号的平均值接近于零的特点，通过时间平均从随机振动信号中提取自由衰减响应。该方法将线性系统在任意激励下的响应看成三个部分组成，即由初位移引起的自由振动、初速度引起的自由振动和随机激励引起的强迫振动。通过大量合理选择的时间片段累加后，获得只有初始位移的自由振动信号。

为了解决信号提取中截取阀值和平均次数的矛盾，本文利用改进的随机减量法［13］，采用了正、负阀值同时截取的提取方法。对于随机响应信号，由正阀值和负阀值截取的信号段具有相同的物理意义。显然，对负阀值截取子信号段变号后再参与叠加平均，就可使参与平均的项增多，使提取的随机特征信号的质量得到提高。

1.4 Hilbert变换和阻尼识别

利用EMD或EEMD方法获得IMF分量后，利用RDT方法提取自由振动衰减信号 X(t)，对其进行Hilbert变换为Y(t):

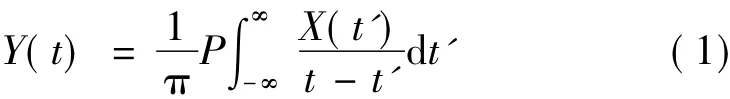
其中P为广义积分的Cauchy主值，由X(t)和Y(t)可以构成一个解析信号:

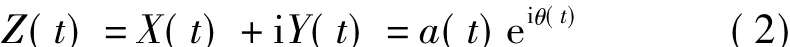
由Hilbert变换得瞬时幅值a(t)、瞬时相位 θ(t)如下:

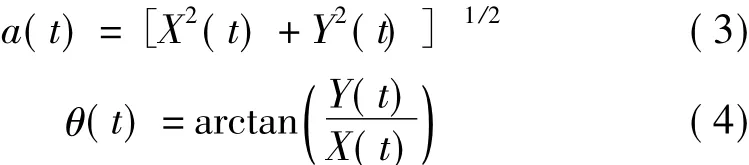
对于小阻尼的单自由度系统，对幅值和相位分别引入对数和微分算子，可得:

式中为阻尼比，C为常数，ω为瞬时频率，ωd为有阻尼系统的频率。设ln a(t)的斜率为p1，θ(t)的斜率为p2(即为频率ωd)，则可识别得阻尼比ζ为:

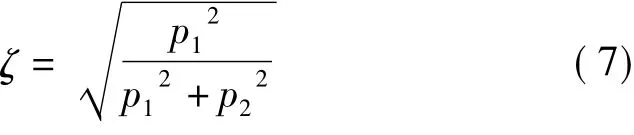
2 某输电塔的气弹模型风洞试验

某输电塔高74.5 m，塔身的平面形状为正方形，其气弹模型采用离散等代刚度法［14］制作，主要考虑输电塔的拉伸刚度相似。模型按1:45缩尺比制作，全塔共有806个杆件，全部采用薄壁铜管和不锈钢无缝毛细管焊接制作，模型通过钢板固定于刚性底座。为了保证受风面积的相似要求，模型杆件外径不足部分首先采用无刚度的泡沫纸外包再用胶带纸封裹，做到几何相似。模型杆件直径为0.4～9.9 mm，杆件壁厚为0.1～0.2 mm，经动力特性标定试验后得到模型相似系数如表1所示，模型的风洞试验照片如图1所示。由于模型为格构式镂空结构，风洞阻塞度不需要修正。

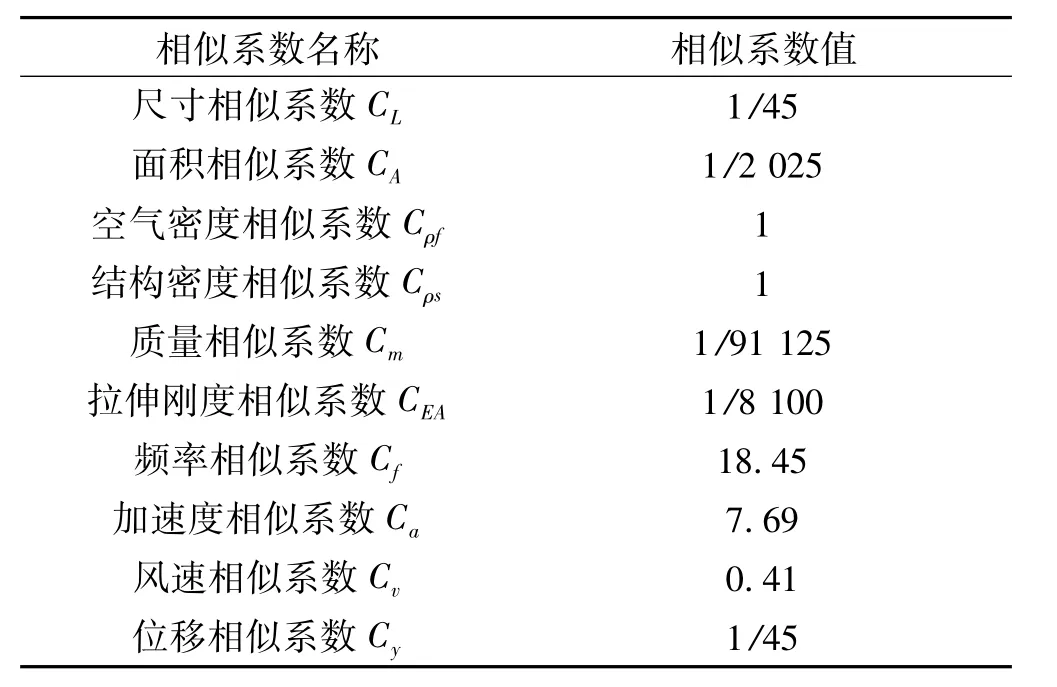
表1 气弹模型的相似系数Tab.1 Similarity coefficients of aero－elastic model

图1 输电塔模型的风洞试验照片Fig.1 Pictures of latticed tower model in wind tunnel

该输电塔的风洞试验在浙江大学ZD－1风洞中进行，试验段长18 m、高3 m、宽4 m。三角尖劈和地面粗糙元置于来流前部，如图1所示，用来模拟B类地貌的大气边界层。根据建筑结构荷载规范［15］要求，B类地貌大气边界层的平均风速V剖面按指数规律变化。对于湍流度Iu剖面，参考日本AIJ规范［16］有:

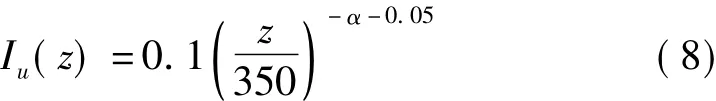
式中z为高度，α为地面粗糙度指数，对于B类地貌取0.16。需要说明的是，试验时由于荷载规范2012版尚未颁布，因此仍采用2001版荷载规范的规定。风洞模拟的风速和湍流度剖面如图2所示，图中平均风速剖面以塔顶高度h的风速为基准进行无量纲处理。由图2可知风洞中很好地模拟了B类地貌的边界层。

在模型上布置12个加速度传感器(每只质量约为2 g)，沿X向(顺线向)、Y向(横线向)各布置6只，灵敏度系数为 0.061 6～0.144 mV/EU，信号采集采用TST5912动态信号测试系统。测试的风向角β及坐标X、Y的方向定义如图3所示。

图2 风洞模拟的平均风速和湍流度剖面Fig.2 Simulated profiles of mean velocity and turbulence intensity in wind tunnel

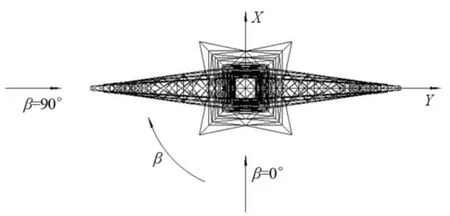
图3 风向角及坐标系统的定义Fig.3 Definition of wind direction and coordinate system

3 EMD与EEMD分解结果的比较

在测试风速18 m/s时0°风向角下输电塔顶部顺线向的加速度时程如图4所示，取1.4 s到1.8 s之间的数据片段进行研究。分别采用EMD和EEMD方法提取各阶IMF模态，为了抑制EMD和EEMD分解的端部效应，采用Rilling等［17］建议的镜像法进行端部数据的处理。

图5给出了EMD和EEMD方法针对图4时程进行IMF分解的结果，计算中EEMD方法所加白噪声幅值取为待分解加速度时程均方根的0.2倍，样本数取500。由图6可知，EEMD方法明显比EMD方法具有更好的分解效果，基于EEMD方法的结果较理想，各阶振荡模态清晰。基于EMD方法的结果存在着一定的模态混叠情况，如图中时间轴1.6 s到1.7 s段，IMF1的结果(图5(a))混叠了IMF2的部分振荡模态(图5(b))，IMF3的结果(图5(c))混叠了IMF4的部分振荡模态(图5(d))。同时基于 EMD方法的结果在IMF4中还存在骑行波(时间轴1.6 s到1.7 s段)，分解结果并不理想。因而EEMD方法分解得到IMF结果更加理想，后面的模态和阻尼识别均基于EEMD方法。

图4 某测点的加速度时程Fig.4 Time history of acceleration on a measured point

4 输电塔阻尼的识别过程

以输电塔顶部横线向的加速度为例，对其在0°风向角、12 m/s试验风速下的加速度时程进行EEMD分解，数据采样频率为500 Hz，采样时间为20 s。对EEMD分解得到的前四阶IMF采用改进的随机减量法提取相应的自由衰减时程c1(t)、c2(t)、c3(t)和c4(t)，如图6所示，随机减量法中的子样本时间长度为0.4 s。

由图6可知，c1至c4均呈现振幅的自由衰减情况，其中c2和c3最为明显，且曲线均比较光滑。将图6的时程进行Hilbert谱变换，获得瞬时频率随时间的变化曲线，其中c3的瞬时频率如图7所示。可知c3对应的频率为28 Hz左右，与输电塔模型横线向的一阶频率刚好吻合，因此EEMD分解后的IMF3代表了输电塔模型横线向的一阶振动。c3时程的自然对数lnα(t)和瞬时相位θ(t)随时间的变化曲线如图8所示，采用拟合方法获得其斜率，再根据式(7)计算得其阻尼比为0.031。

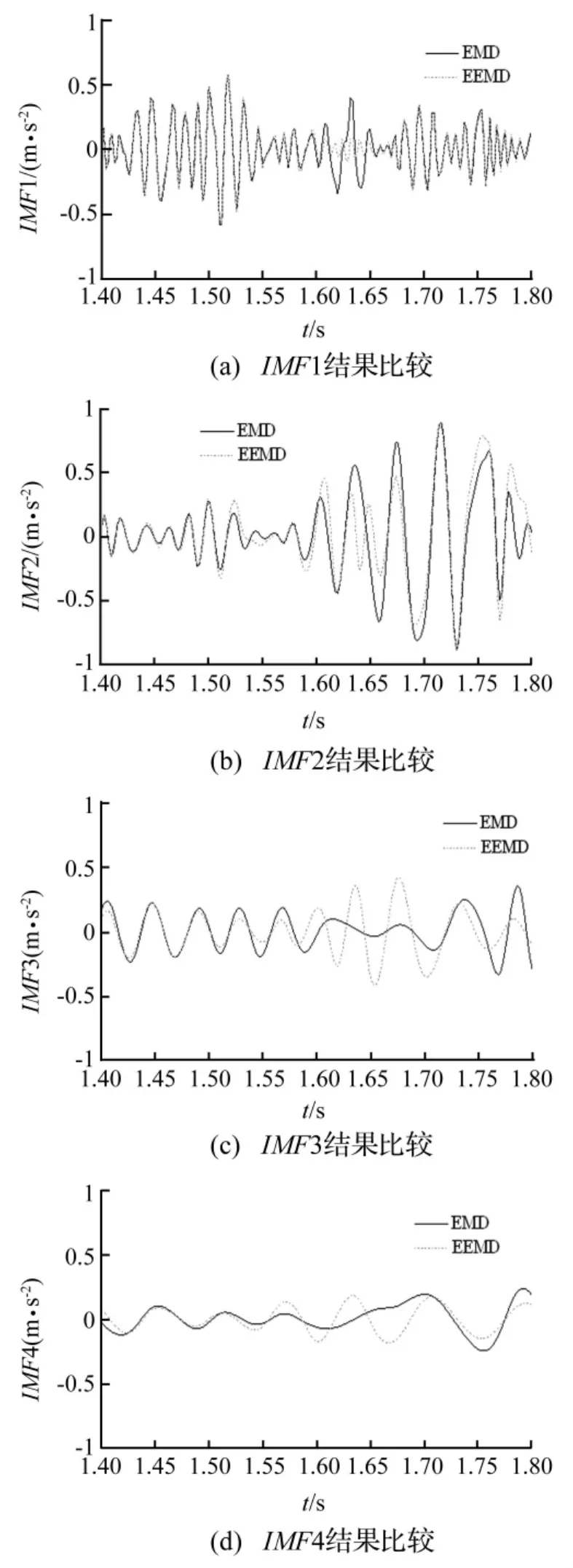
图5 EMD和EEMD分解模态的比较Fig.5 Comparison of decomposition modes obtained from EMD and EEMD methods

5 输电塔总阻尼的识别结果

在风洞中对输电塔模型进行6个风速(8 m/s、10 m/s、12 m/s、14 m/s、16 m/s、18 m/s) 和 7 个风向角(0°、15°、30°、45°、60°、75°、90°)下的测振试验。根据顶部的加速度测试结果，采用EEMD分解法结合改进的RDT法和Hilbert变换，识别主IMF对应的自振频率和总阻尼比，其中顺线向的数据如图9所示，横线向的数据如图10所示。需要说明的是，图中的阻尼为风荷载作用于输电塔上的总阻尼比，包含了结构阻尼和气动阻尼。结构阻尼通常可以采用敲击法进行识别，在实际操作中发现测试获得的结构阻尼比较离散，其原因主要为阻尼与振动幅度有很大的关系，通常认为结构阻尼随着振动幅度的增大而增大［18］。因此本文不分离出结构阻尼和气动阻尼，采用总阻尼来表示。

由图9可知，输电塔顺线向的自振频率总体上随着风速的增大而呈减小趋势，在文献［6］中也发现该规律，频率减少的一个原因是与高风速下总阻尼增大有关;顺线向的总阻尼随着风速的增大总体上呈单调增大趋势。由图10可知，输电塔横线向的自振频率总体上随着风速的增大而呈减小趋势，但离散度比图9中的顺线向数据大;而横线向总阻尼的规律性不明显，在风洞风速10 m/s时有一个突增，然后随着风速增大呈略有增加的趋势。

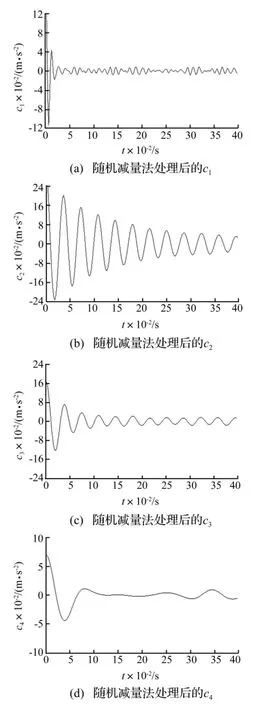
图6 各阶IMF采用随机减量法处理后的时程Fig.6 Time histories of IMF modes after treatment of RDT

图7 c3的瞬时频率Fig.7 Instantaneous frequencies of c3

图8 ln a(t)和θ(t)随时间的变化曲线Fig.8 Curves of ln a(t)and θ(t)with respect to time

图9 顺线向频率和阻尼的识别Fig.9 Identification of frequency and damping in along-line direction

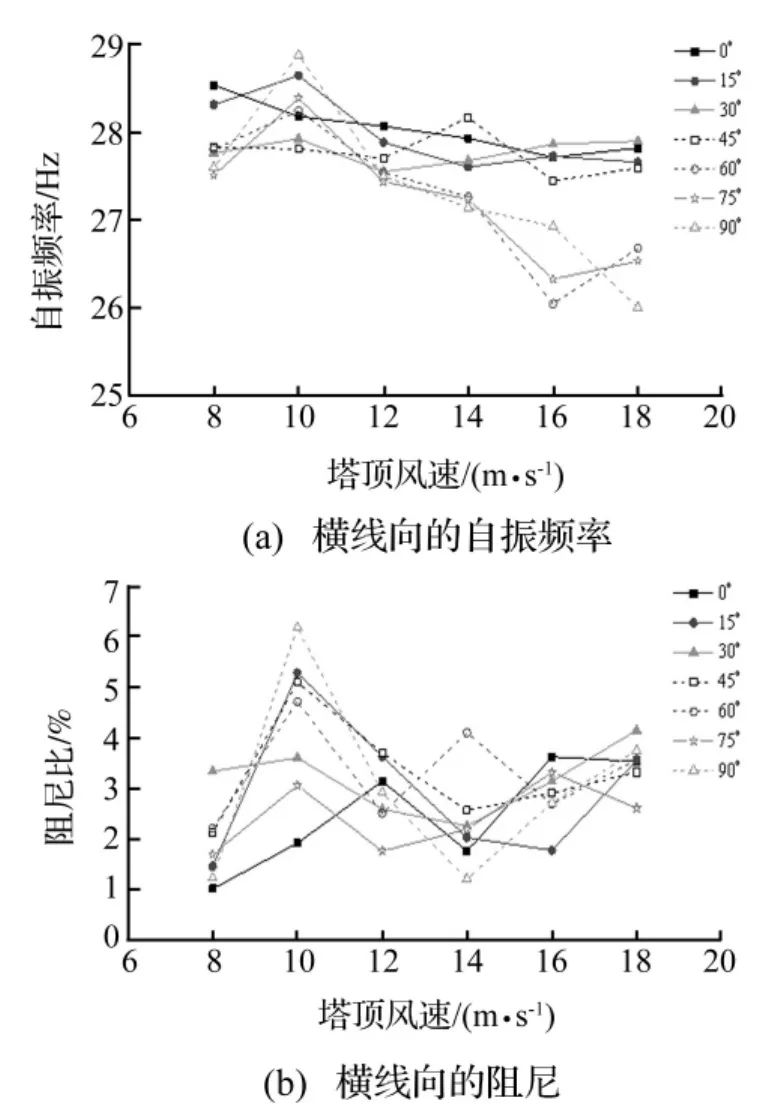
图10 横线向频率和阻尼的识别Fig.10 Identification of frequency and damping in cross-line direction

针对图9和图10所反映的输电塔顺线向和横线向的振动特性，作讨论如下。输电塔的风致振动主要由风绕输电塔杆件引起，风穿过输电塔杆件会产生复杂的空气动力学现象，包含了漩涡脱落、涡激振动、尾流干扰等。相比而言，顺线方向的气动现象(风穿过两片桁架)比横线方向的气动现象(风在横担处需要穿越很多层桁架，具体见图1)相对简单一些，因而输电塔的频率和阻尼随风速风向变化的规律性在顺线方向(见图9)比在横线方向(见图10)要好很多很多。文献［19］从风力谱角度也提到:顺风向(对于0°风向即为顺线向)脉动风力谱是一种典型的纵向风湍流谱，而横风向(对于0°风向即为顺线向)力谱较为复杂，这从另一个方面支持了本文的观点。

6 结论

本文研究基于EEMD的阻尼特性识别方法和输电塔阻尼分布特性，有以下结论:

(1)本文实例发现从加速度时程中分解IMF时采用EEMD方法比EMD方法具有更好的分解效果，基于EEMD方法的IMF时程振荡模态更清晰，而基于EMD方法的结果存在着一定程度的模态混叠，因此推荐使用EEMD方法。

(2)采用EEMD分解法结合改进的RDT法和Hilbert变换，可以从结构响应时程中识别出主IMF对应的频率和阻尼，在动力特性识别时推荐使用。

(3)输电塔顺线向的自振频率总体上随着风速的增大而呈减小趋势，顺线向的总阻尼随着风速的增大而增大，而横线向频率和阻尼随风速变化的规律性不明显。

(4)风穿过输电塔杆件会产生复杂的空气动力学现象，包含了漩涡脱落、涡激振动、尾流干扰等。相比于顺线方向，输电塔在横线方向时风需要绕过更多层桁架，反应在动力特性上便是顺线方向的动力特性随风速变化的规律性更好。

［1］汪江，杜晓峰，田万军，等.500 kV淮蚌线淮河大跨越输电塔振动测试与模态识别［J］.中国电力，2009，42(2):30－33.WANG Jiang， DU Xiao-feng， TIAN Wan-jun， et al.Dynamic testing and model identification of long-span power transmission tower located in 500 kV Huaibeng Line［J］.Electric Power，2009，42(2):30 －33.

［2］何敏娟，闫祥梅，张益国，等.两相邻输电塔的同步环境脉动实测试验研究［J］.振动与冲击，2009，28(11):155－158.HE Min-juan， YAN Xiang-mei， ZHANG Yi-guo， et al.Synchronous test study of two adjacent transmission tower undergoing ambient excitations［J］.Journal of Vibration and Shock，2009，28(11):155 －158.

［3］胡宇滨，马人乐.江阴500 kV输电塔动力性能测试［J］.结构工程师，2002，3:62－66.HU Yu-bin，MA Ren-le.Site experiment of dynamic behavior for Jiangyin 500 kV transmission tower［J］.Structural Engineers，2002，3:62 －66.

［4］应怀樵，刘进明，沈松.半功率带宽法与 INV阻尼计法求阻尼比的研究［J］.噪声与振动控制，2006，2:4－6.YING Huai-qiao，LIU Jin-min，SHEN Song.Half-power bandwidth method and INV damping ration solver study［J］.Noise and Vibration Control，2006，2:4 －6.

［5］李正良，肖正直，韩枫，等.1 000 kV汉江大跨越特高压输电塔线体系气动弹性模型的设计与风洞试验［J］.电网技术，2008，32(12):1－5.LI Zheng-liang， XIAO Zheng-zhi， HAN Feng， et al.Aeroelastic model design and wind tunnel tests of 1 000 kV Hanjiang long span transmission line system［J］.Power System Technology，2008，32(12):1 －5.

［6］任坤，李正良，肖正直，等.环境激励下特高压输电塔线体系气动阻尼的识别［J］.重庆工学院学报(自然科学版)，2009，23(7):64 －68.REN Kun， LI Zheng-liang， XIAO Zheng-zhi， et al.Aerodynamic damping identification of UHV transmission line system under ambient excitation［J］.Journal of Chongqing Institute of Technology(Natural Science)，2009，23(7):64－68.

［7］郭勇.大跨越输电塔线体系的风振响应及振动控制研究［D］.杭州，浙江大学，2006.

［8］熊铁华，梁枢果，邹良浩.基于完全气弹模型风洞试验输电塔风荷载识别［J］.建筑结构学报，2010，31(10):48－54.XIONG Tie-hua，LIANG Shu-guo，ZOU Liang-hao.Wind loading identification of transmission towers based-on wind tunnel tests of full aero-elastic model［J］.Journal of Building Structures，2010，31(10):48 －54.

［9］ Huang N E，Shen Z，Long S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London(series A)，1998，454(1971):903－995.

［10］项国通.格构式圆截面钢管塔风荷载特性的风洞试验研究［D］.杭州，浙江大学，2013.

［11］ Wu Z H， Huang N E. Ensemble empirical mode decomposition:a noise-assisted data analysis method［J］.Advances in Adaptive Data Analysis.2009，1(1):1 －41.

［12］ Huang N E，Shen Z，Long S R.A new view of nonlinear water waves:the Hilbert spectrum［J］.Annual Review of Fluid Mechanics.1999，31(1):417 －457.

［13］张西宁，屈梁生.一种改进的随机减量信号提取方法［J］.西安交通大学学报，2000，34(1):106－107.ZHANG Xi-ning，QU Liang-sheng.Improved method for extracting of random decrement signal［J］.Journal of Xi’an Jiaotong University，2000，34(1):106 －107.

［14］郭勇，孙炳楠，叶尹，等.大跨越输电塔线体系气弹模型风洞试验［J］.浙江大学学报(工学版)，2007，41(9):1482－1486.GUO Yong，SUN Bing-nan，YE Yin，et al.Wind tunnel test on aeroelastic model of long span transmission line system［J］.Journal of Zhejiang University(Engineering Science)，2007，41(9):1482 －1486.

［15］建筑结构荷载规范(GB50009－2001)［S］.北京:中国建筑工业出版社，2002.

［16］ Architectural Institute of Japan.Recommendations for loads on buildings［M］. Japan: Architectural Institute of Japan，2004.

［17］ Rilling G，Flandrin P，Goncalves P.On empirical mode decomposition and its algorithms［C］.IEEE Workshop on Nonlinear Signal and Image Processing NSIP－03，Grado(I)，2003.

［18］嵇学培，谢壮宁，李小康.广州西塔风致响应和气动阻尼特性的试验研究［J］.土木工程学报，2009，42(7):58－64.JI Xue-pei， XIE Zhuang-ning， LI Xiao-kang. An experimental study on the wind induced response and aerodynamic damping of Guangzhou west tower［J］.China Civil Engineering Journal，2009，42(7):58 －64.

［19］张庆华，顾明，黄鹏.格构式塔架风力特性试验研究［J］.振动与冲击，2009，28(2):1－4.ZHANG Qing-hua，GU Ming，HUANG Peng.Experimental study of wind force on latticed tower［J］.Journal of Vibration and Shock，2009，28(2):1 －4.