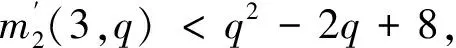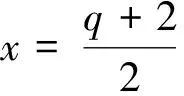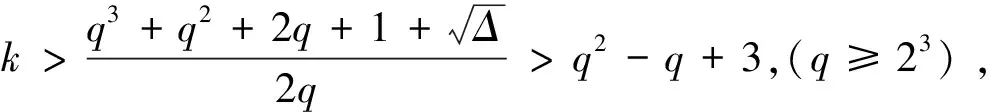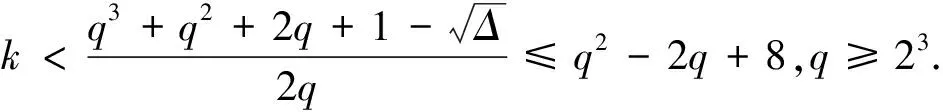关于的上界*

欧 璐，曹金明

(1．湖南大学 数学与计量经济学院，湖南 长沙 410082;2．湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082)

1 预备知识

m2(3,q)=q2+1,q为偶数并且q>2[1-2];

m2(3,q)=q2+1,q为奇数[3];

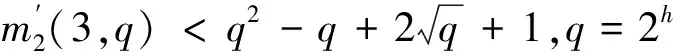
本文将给出结果：

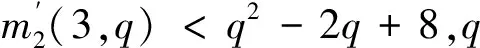
2 需要的有关结论

对任意一个PG(n,q)上k-cap集K而言，我们定义满足|l∩K|=i的这样一条直线l为i-割线.而一条1-割线我们也称为切线；一条2-割线称为二度割线；一条0-割线称为外部线.令t为过K中一点P到K的切线的条数.而σi(Q)为过K外一点Q到K的i-割线的条数，其中i=1,2.因此，有下面的等式成立：

1)t+k=qn-1+…+q2+q+2；

2)σ1(Q)+2σ2(Q)=k.

引理2[8]如果K为PG(n,q)上的完全k-cap，并且q为偶数，那么对PG(n,q)K中的任一点Q都有σ1(Q)≤t.

引理3设K为PG(3,q)上完全k-cap且k

证明令l1,…,lt为过K中一点P的t条切线，考虑以下3种情况：

① 过任何一条切线li恰恰只存在一个平面πli使得|πli∩K|≤2(1≤i≤t).

假设过点P仅仅只有唯一一个平面，不妨设为π，使得|π∩K|≤2，那么就有：πli=π(i=1,…,t).所以经过点P到K的所有切线都在π上，那么有t≤q+1，由等式(1)得到：k≥q2+1，与题设条件相矛盾.

所以过点P至少存在两个不同的平面πj(j=1,2)，满足|πj∩K|≤2.而每一个平面πj(j=1,2)至少都包含q条过点P到K的切线，因此有：t≥2q-1=2(q-1)+1.

② 通过某一条切线，假设为li0，存在两个不同的平面，它们与K相交的点不多于两个(1≤i0≤t).

因为li0是K的一条切线，由caps的定义，所有过li0的平面交K至多有q+1个点.计算所有经过切线li0的q+1个平面中那些属于K中的点的个数得到：k-1≤2+(q-1)q，即k≤q2-q+3，由等式(1)有：t≥2q-1=2(q-1)+1.

③ 经过某一条切线，设为lj0，过它的所有平面中没有一个满足与K的交点不多于2个(1≤lj0≤t).

即过切线lj0的任何一个平面πj都满足|πj∩K|≥q(1≤j≤q+1).又因为有|πj∩K|≤q+1成立，所以由引理1，得知πj∩K能够被扩充为一个完全(q+2)-arc.而每个(q+2)-arc必然会交lj0于不同于点P的一点，设为Pj.如果q+1个Pj点互不相同的话，在lj0上就会出现q+2个点，这是不可能的.所以必定存在其中的两点是相同的点，不妨设它们为P1和P2，即有P1=P2.

这样，如果要计算过点P1到K的切线就得同时考虑点P1到π1∩K上和到π2∩K上这两部分的直线.因为P1不属于K，所以有：σ1(P1)≥2(q-1)+1，由引理2有：t≥σ1(P1)，所以有t≥2(q-1)+1成立.

3 定理及其证明

1)假设存在一个平面π0，满足4≤|π0∩K|≤q-2.令l为过K中点的P到K的任意一条切线，考虑下面两种情况：

计算过l的q+1个平面上属于K中的点的个数得到：

q≥28．

假设其中的任意一点都被重复计算不超过3次，则有：

q2+2q-8

当q≥24时，上面的不等式矛盾.从而在这些点中一定存在一个属于π0K的点，设为P0，满足过该点至少有4个平面使得这些平面与K的交集并上该点成为一个arc,所以：

k≤q2-2q+8.

2)对任意平面：π有:|π∩K|≥q-1或者|π∩K|≤3.

①假设存在平面π0使得|π0∩K|=3或者|π0∩K|=q-1，则在π0上有3(q-1)条切线.

i)设l为K的任一条切线，假设过l至少有3个平面使得它们与K的交点小于等于3，用类似的方法计算过l的q+1个平面上属于K中的点，就得到：

k-1≤3×2+(q+1-3)q=q2-2q+6,

k≤q2-2q+7

ii)否则不考虑π0的话，过l至少有q-2个平面，它们与K的交点至少为q-1个.由引理1，这些平面均可以扩充为一个更大的arc，且这些arc与l有唯一不属于K的交点.同(1)中②的证明类似，在π0上总共有3(q-1)(q-2)个这样的交点.

假设其中的任意一个交点都被重复计算不超过2次，则有：

q2-11q+5<0．

显然，当q≥24时，上面的不等式矛盾.从而一定存在属于π0K的一点，不妨设为P1，满足过该点至少有3个平面，它们与K的交集并上该点就成为一个arc，则有：

k≤q2-2q+8．

②对任意平面π有|π∩K|≥q或者|π∩K|≤2.

i)设P∈K，过点P至少有3个平面，使得它们与K的交点不超过2，则有：

k≤q2-2q+8．

ii)最多存在两个平面，不妨设为π1和π2，它们与K的交点不超过2，从而由引理3有t≥2(q-1)+1成立，所以有：

k≤q2-q+3．(*)

设l1,…,lt-1为过P点到K的不考虑π1∩π2这条直线的所有切线.考虑其中的任一条lj.

因为过lj的所有平面中至多只含有π1和π2中的一个，所以至少有q个平面，它们与K的交点不少于q.计算过切线lj的所有平面中属于K中点的个数，其中设mh为与K相交h个点的平面个数：

k-1≥1+mq(q-1)+qmq+1=

1+(q-mq+1)(q-1)+qmq+1=

q2-q+1+mq+1．

假设mq+1≥2，则有k≥q2-q+4，这与(*)相矛盾.

所以过lj至少有q-1个平面，设为βi，满足|βi∩K|=q.

下面考虑其中任意一个平面βi.对于∀Q∈βiK且Q为lj上的点，则有：σ1(Q)+2σ2(Q)=q，由于q与2σ2(Q)都为偶数，得到σ1(Q)也为偶数，则σ1(Q)≥2，即过点Q除切线lj外，至少还有一条切线在βi中.考虑以下几种情况.

ⅱ)在lj上存在不属于K的点Q2，使得过lj至少存在两个平面πi，使得πi∩K∪{Q2}是πi上的arc(其中i=1,2).这时，计算过点Q2到K的所有切线有：

σ1(Q2)-1≥2(q-1)+(q-3)=3q-5,

t≥σ1(Q2)≥3q-6,

k≤q2-2q+8．

ⅲ)在lj上任意不属于K的点Q1，使得过lj恰有一个平面π，使得π∩K∪{Q1}为平面π上的arc.考虑以下两种情况.

a)还存在另外一条切线L，在L上至少存在平面π′，使得π′∩K∪{Q1}为平面π′上的arc.这时，计算过点Q1到K的所有切线有：

t≥σ1(Q1)≥2q+q-2≥3q-2,

k≤q2-2q+4≤q2-2q+8．

b)任意切线上的不属于K的点Q1，过点Q1最多只有一个平面π″，使得π″∩K∪{Q1}为平面π″上的arc.这时，计算所有这些点的个数有：

k(t-1)q≤(q+1)(q3+q2+q+1-k)．

又t+k=q2+q+2，代入上式有：

qk2-(q3+q2+2q+1)k+(q+1)(q3+q2+q+1)≥0．

解这个二次不等式，并令

Δ=(q3+q2+2q+1)2-4q(q+1)(q3+q2+q+1)．

那么有：

至此，原命题全部得证.

[1] QVIST B. Some remarks concerning curves of the second degree in a finite plane[J].Anm Acad Sci Fenn Ser A，1952,(12):341-345．

[2] STORME L, THAS J A. New apper bounds for the sizes of caps in finite projective spaces[J]. Geom, 2002,(73):176-193.

[3] BOSE R C. Mathematical theory of the symmetrical factorial design[J].Sankhyä,1947,(8):107-166．

[4] STORME L, SZÖNYI T. Caps inPG(n,q),qeven,n≥ 3[J]. Geom Dedicata, 1993, (45):163 -169．

[5] CHAO J M. On the size of a cap inPG(n,q) withqeven andn≥ 3[J]. Geometriae Dedicata,1999,(74):91-94．

[6] FERRET S, STORME L. On the size of complete caps in PG(3, 2h)[J]. Finite Fields Appl, 2004,(10):306-314.

[7] HIRSCHFELD J W P. Projective geometries over finite fields[M]. Oxford: Oxford University ,1979．

[8] HIRSCHFELD J W P, THAS J A. General galoi geometries[M]. Oxford: Oxford University Press,1991．