待定系数法求自然数幂和
2014-09-17李卫高
李卫高
(漯河医学高等专科学校,河南漯河462002)
自然数幂和是一个很古老的问题,人们很早就熟悉了低次幂求和公式,也提供了低次幂求和的宝贵经验.直到现在,任意次自然数幂求和仍是人们关心的话题,其中所用的方法各种各样,结果也不尽相同.笔者通过利用二项式定理展开一个和式,并加以整理,得到了一个含有任意次自然数幂和的式子.经过赋值合并,给出了隔次自然数幂和组合公式,由此公式,用待定系数法,最终得到了和伯努利公式类似的幂和公式.
由
+…
(1)
令x=-1,得
(2)
(2)-(1),得
(3)
(3)式是一个关于隔次自然数幂和组合公式,以下为方便起见,在书写与m有关的有限项连加式的时候,因最后一项与m的奇偶性有关,只写前面的项,后面略去.
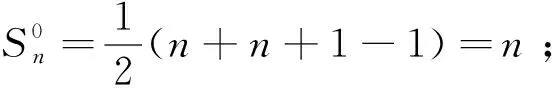


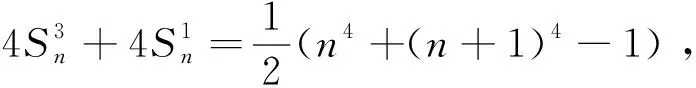


(3)式左端,
比较左右两端的系数,得
所以
其中λk由如下式子确定:
例如

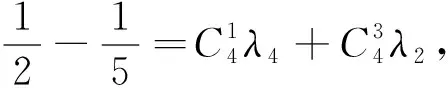
进一步计算可算出

n=input(′n=′)
A(1,1)=factorial(2);b(1)=1/2-1/3;
for k=2:1:n
for j=1:k
A(k,j)=factorial(2*k)/[factorial(2*(k-j)+1)*factorial(2*j-1)];
end
b(k)=1/2-1/(2*k+1);
end
x(1)=1/12;
for k=2:1:n
for j=1:k-1
b(k)= b(k)-A(k,j)*x(j);
end
x(k)=b(k)/A(k,k);
end
x
输入n=20:


查阅资料可以发现,上述结果和历史上伯努利的幂和公式是类似的.
雅谷·伯努利(1654-1705)在《猜度术》(1713)中得到任意次幂的求和公式,根据他的原著,此式表示为
式中A=1/6,B=-1/30,C=1/42,D=-1/30, …是著名的伯努利数.
[参 考 文 献]
[1] 罗见今.自然数幂和公式的发展[J].高等数学研究,2004,7(4):56-61.
[2] Heath T L. 阿基米德全集. 朱恩宽,李文铭,等译[M].西安:陕西科学技术出版社, 1998.
