路面平整度的时间序列模型
2014-09-17王佳秋马松林
王佳秋, 王 葳, 邓 慧, 马松林
(1.黑龙江科技大学理学院,哈尔滨150027; 2.哈尔滨工业大学交通学院,哈尔滨150001)
1 引 言
2 道路基础描述
2.1 道路等级介绍
道路的形式化表达是分析和研究的基础,道路描述或者用时域的统计数字特征——道路不平顺均值、方差、时域或时差域的更高阶统计量(高阶矩)描述,或者用频域的Fourier频谱、PSD函数、谱矩来描述.在我国道路功率频谱密度(PSD)函数由幂律函数形式给出[1],将功率频谱密度PSD描述转换成有理函数形式.定理指出只要平稳序列的谱密度是有理函数形式,则它一定是一个ARMA或AR时间序列模型,这为应用时序方法建立道路模型奠定了理论基础.
有理函数功率谱参数估计不平路面度功率谱的有理函数形式之一为[2]
(2-1)
式中A为常数(1/m);Q为常数(m);σ为空间频率(c/m).
文献中仅给出了沥青、水泥及粗糙路面的A,Q数值,而未给出通用的将路面分为五级的数值.1987年Robson等人提出了路面不平度功率谱的一种幂函数公式,该式可转变成如下形式:
(2-2)
式中Csp为路面不平度系数(m2/c/m),σ1为空间频率下限(值为0.1c/m),σ2为空间频率上限(值为2c/m).式(2-1)中的A及Q是常数,式(2-2)中的Csp由实验测得.而两式描述的是同一随机过程,因此式(2-1)中的常数可由给定的式(2-2)通过非线性参数估计的方法确定,其模型为
(2-3)
式中c1,c2为常数,m为所取空间频率σ的个数.
公式(2-3)构成典型的非线性约束最优化问题,一些通用软件可用于该问题的求解,优化结果列于表2-1中.

表 2-1 参数估计值
上述主要将功率频谱密度描述转换成有理函数形式,介绍关于道路级别的评定方法.这里只介绍了五个级别路面的相关数值,为后文给出一维路面高度数据并且评定其路面等级提供参考.
3 非标准道路时序模型
已知测量道路数据序列即道路样本{xi}且足够长,建立模型的过程如下:
3.1 对测量数据序列进行预处理
包括剔除异常值,数据平滑化,非平稳序列经一次或多次差商(差分)后的平稳化,非零均值序列的零均值化等.
抽取某医院在接收的患有2型糖尿病的晚期非小细胞肺癌的患者,共136例,且所选的所有患者均符合国际通用的糖尿病和非小细胞肺癌的诊断标准,将这些患者平均且随机的分为两组,即对照组和试验组,每组68例。其中,试验组患者包括男性病患34例,女性患者 34 例,年龄38~74 岁,平均(54.8±12.4)岁;对照组包括男性患者33例,女性患者35例,年龄39~76岁,平均(55.3±13.1)岁。对两组的一般资料统计学处理,结果发现差异无统计学意义(P>0.05),具有可比性。
3.2 模型识别和定阶
3.3 确定模型参数和检验模型适用性
对AR模型前已确定阶次,故容易得到模型参数的估计值.常用的估计模型参数的方法有矩方法、最小二乘法和极大似然法.当样本满足正态分布且足够长时,采用最小二乘法估计参数可得到与采用极大似然法基本一致的结果,最小二乘法就是使得残差平方和达到最小条件下所得到的对未知参数的估计值.由于时序模型的谱密度仅依赖于有限参数——自回归系数、滑动平均系数及输入白噪声的方差,因此可以通过对时序模型的谱估计转化得到对模型参数的估计,而其中参数化的谱估计以最大熵谱估计方法为代表,与AR模型的线性自回归不同,ARMA模型的回归是非线性的,不能用最小二乘法估计出模型的参数,而需用非线性最小二乘法——泰勒级数展开线性化或广义最小二乘法,其计算过程复杂、计算量很大.常用矩方法估计ARMA模型参数,也可用二级最小二乘法估计模型参数,即首先导出一足够高阶的AR模型,然后利用AR模型估计ARMA模型的输入输出互相关特性并进而确定其参数.
进行模型适用性检验,时序方法中发展了一系列的准则以检验模型的适用性,这些准则主要有:白噪声检验准则,残差平方和检验准则.适用性检验对于时序模型而言,实质上就是模型定阶,尤其对ARMA模型,可以称这些准则为定阶准则.如果模型通过了适用性检验则模型是正确的,且具有所需的模拟精度,该模型能被外推用于道路数据库模型中.
4 道路平整度实例分析
4.1 数据的采集
本文所用到的数据是由道路综合检测车对实际路段测得.该设备是由哈尔滨工业大学交通学院侯相深,马松林,王华等人自行开发设计,是采用电脑自动化检测技术、以测距传感器和定位传感器为工具的多点车辙测量仪,可通过USB接口的传输线将采集的数据存入在检测车上的便携式处理器,进行数据处理.检测车由16个传感器组成,可以同时测量一个行车道断面的16个点,并且可以连续密集的采集路面表面的数据.经室内标定,该仪器的测量相对误差均在1%以下,如表4-1所示,完全可以满足工程要求[3].

表 4-1 标定的相对误差(%)
本文所采用的数据是道路综合所得,横向一共有16个测点,每点间隔0.2米,截取其中50米路段的数据进行实际建模.采集的车辙数据经去除抖动处理后,本文只研究一维数据,一共250个数据.见表4-2.

表4-2 路面高度数据(mm)
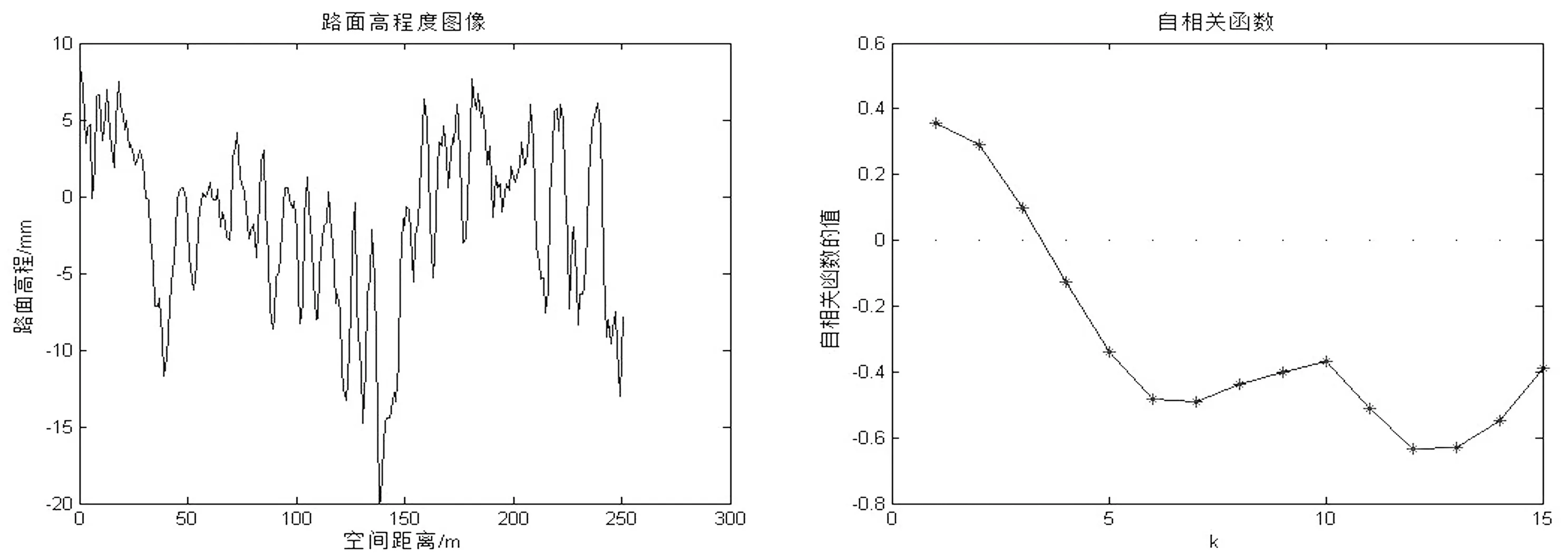
图1 路面高程度 图2 零均值化序列的自相关函数
4.2 数据的处理
由于时间序列模型建立在严密的统计学理论基础之上,因此对样本的容量、样本的性质有一定的要求.首先,它要求样本容量最好要50个以上只有这样才使得后模型诊断与检验有意义;其次,它要求样本时间序列必须是一个平稳过程.
选择的样本Xt除了满足上述两个条件以外还要要满足使用近期的数据这样对以后路面研究的实用性更强.本文的样本选取长度为50米.由于检测车每隔0.2米一测,所以一共250个数据点,显然,该序列为随机时间序列,其容量满足条件要求.用Matlab软件画出该序列的趋势图,如图1所示.通过对时序图的趋势观察,发现该时间序列不满足平稳性的条件,由此可见该随机过程为非平稳的时间序列.
4.3 平稳性的检验
由时间序列图可以看出有明显的趋势性,需要将时间序列平稳化.在前面已经给出了平稳化的方法中较有效地方法是采用差分法,若一次差分后序列还不满足平稳性条件,可以进行二次差分,直到得到的序列是平稳的时间序列为止.
首先进行一步差分,其差分的格式为
ΔXk=Xk+1-Xk,k=1,2,…,95.
记
Yk=ΔXk,k=1,2,…,95,
可得一次差分后的时间序列.再对一阶差分后的数据进行零均值化.
采用自相关系数图检验法[4].如果差分后所得的平稳时间序列为白噪声时间序列,那么该序列的自相关系数将近似服从均值为零,所以可给出置信度为95%的置信区间.若在该区间内则说明样本间存在相关性,即可得出该序列并非白噪声序列.
样本自协方差函数为
样本自相关函数
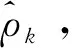

表4-3 零均值化后的自相关系数
可利用计算出的数据画出差分前后的自相关函数图检验序列的平稳性.如图2.
5 道路平整模型分析
5.1 模型的识别和估计
对模型的识别,我们一般通过考察平稳时间序列的自相关和偏自相关系数的性质来进行模型的选择.通常根据差分后自相关函数图,很难确定自相关系数的趋势,为此还需进一步观察样本偏相关系数的性态.利用Matlab软件求出差分后样本偏相关系数的数据如表5-1所示.

表5-1 零均值化后的偏相关系数
一般而言,如果自相关系数表现出拖尾而偏自相关系数表现出p阶截尾,则选择AR(p)模型;如果自相关系数表现出q阶截尾而偏自相关系数表现出拖尾,则选择MA(q)模型;如果自相关系数和偏自相关系数均表现出拖尾,则选择ARMA(p,q)模型.所谓偏相关函数φkk截尾,指
即φkk在k等于p时不为0,在p以后都等于0,图像像截断了尾巴一样,而且尾巴截断在k=p的地方.
我们再用AIC和BIC准则来确定模型的阶数[5],其中
当样本长度为N,p,q达到某一对数值时,AIC达到最小,此时的p,q为最佳的模型阶数.
本文应用EVIEWS软件运行,可以得出ARMA(2,0)即AR(2)的AIC值最小,所以该模型为最佳拟合模型.
自相关图像是拖尾的,偏相关图像是结尾的,所以应该用AR(P)模型.p由偏相关函数来确定,
YT=φ1YT-1+φ2YT-2+εT.
通过EVIEWS软件进行极大似然估计估计模型参数,求得
φ1=0.434968,φ2=-0.221342,
计算可得最终线型模型为
YT=0.434968YT-1-0.221342YT-2+εT.
回代YT=ΔXT=XT+1-XT得到原时间序列的的线型为
XT+1-XT=0.434968(XT-XT-1)-0.221342(XT-1-XT-2)+εT.
整理得
XT+1=1.434968XT-0.656310XT-1+0.221342XT-2+εT.
5.2 模型的残差检验
参数估计后,我们对模型的残差序列进行白噪声检验,若残差序列不是白噪声序列,需要进一步改进模型;如果残差序列的样本自相关系数都落入随机区间内,即没有任何自相关个别的在统计上显著,那么可以说残差序列是纯随机的[6].对AR2进行检验得到图3,可以看出残差序列的样本自相关系偏相关系数数都落在正负0.2随机区间内,因此该模型是合适的.

图3 残差分析
5.3 预测、检验和评价
以251个数据的最后三个数据-13.07,-10.4,-7.87为初始数据带入模型
XT+1=1.434968XT-0.656310XT-1+0.221342XT-2+εT.
对后三个数据进行外推,外推数据如下表并且列出了真实值,计算出绝对误差和相对误差.结果见表5-2.
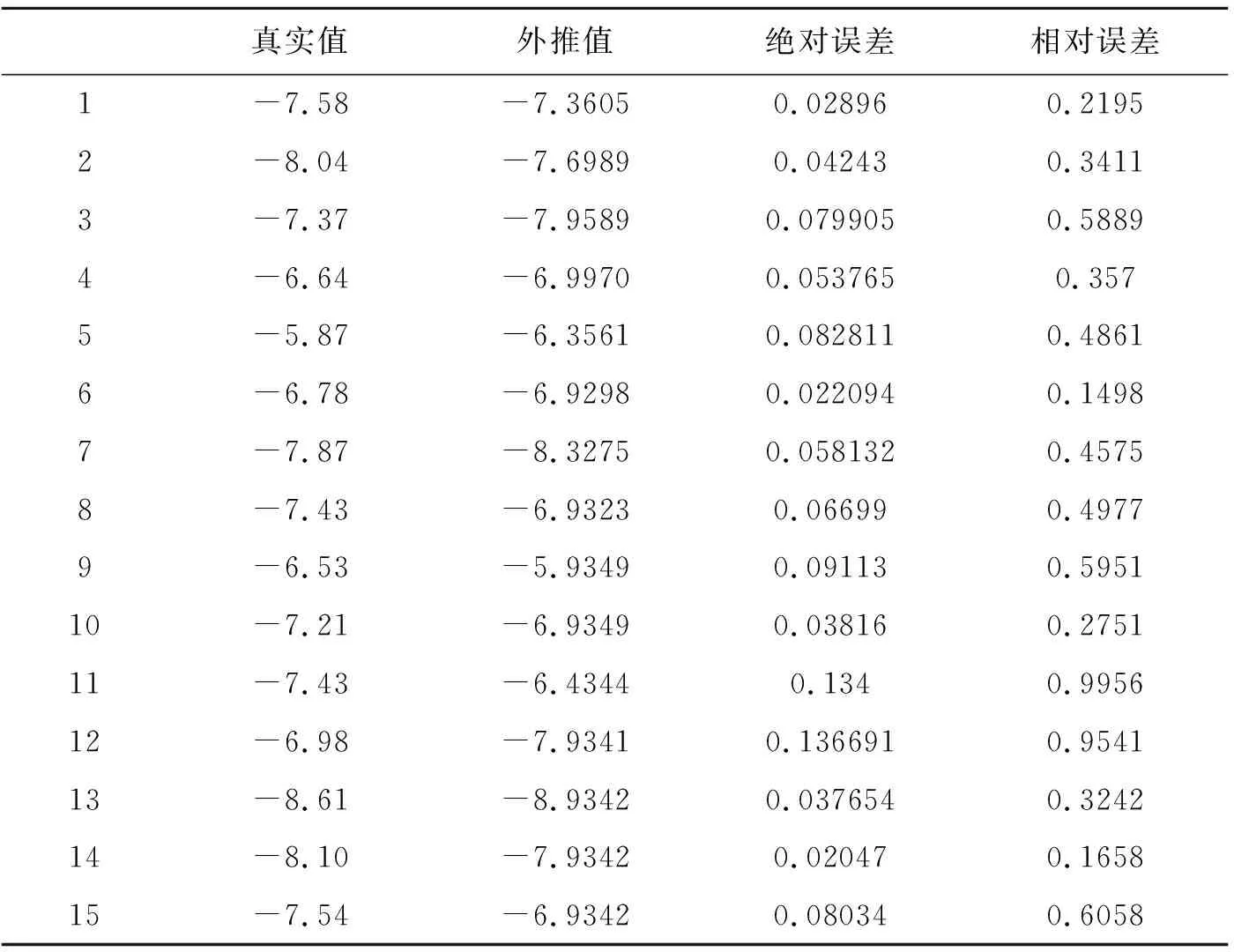
表5-2 外推结果
从模型的预测数据可得出最大相对误差为0.9956%,最大绝对误差为0.134.本文参考数据是道路实测路面高度,经过计算得出该数据为非标准道路路面数据,模型的预测精度比较高.
[参 考 文 献]
[1] 檀润华,陈鹰,路甬祥.路面对汽车激励的时域模型建立及计算机仿真[J].中国公路学报,1998,11(3):96-102.
[2] 谢伟东,王磊.随机信号在路面不平度仿真中的应用[J].振动测试与诊断,2005,25(2):126-130.
[3] 姚金斌,李志林.股市预测的一个随机时间序列模型及其实证[J].吉首大学学报,2008,5(2):1-3.
[4] 王行建,刘欣.ARMA时间序列模型的研究与应用[J].自动化技术与应用, 2008,27 (10):1-3.
[5] 黄建洪,陈志伟,傅戈雁.时间序列预测模型的建模方法与应用[J].机械制造,2007,11(5):1-2.
[6] 侯相深.车辙仪的开发要点[J].哈尔滨工业大学学报,2004:1-3.
