适用于TATB,RDX,HMX 含能材料的全原子力场的建立与验证

金 钊 刘 建 王丽莉 曹风雷 孙 淮,*

(1上海交通大学化学化工学院,上海200240;2中国工程物理研究院计算机应用研究所,四川绵阳621900)

1 引言

含能材料在航天、国防、能源领域有着重要的应用.采用理论与计算化学方法研究含能材料能够弥补实验研究方法的不足,提高研发效率.与量子化学方法对比,基于分子力学力场的模拟方法能够在较大尺度下预测材料特别是含能材料与高分子复合材料的物理性质,1-7但力场参数的不足严重阻碍了这一类方法的应用.

文献中已有一些关于含能材料的分子力学力场的报道.Sorescu等8,9采用刚性分子模型开发了环三亚甲基三硝胺(RDX)和环四亚甲基四硝胺(HMX)的力场,分子间的相互作用使用库仑和Buckingham势函数(简称SRT力场)来表示.计算结果显示该力场可以比较准确地描述晶体的结构.Smith和Bharadwaj10开发了HMX的全原子力场,其力场函数包括了分子内和分子间两部分,其中分子内部分用简谐振动函数描述键长、键角,余弦函数描述二面角,而分子间的非键项采用Buckingham势函数和修正的库仑项(简称SB力场).Boyd等11开发了RDX的全原子力场,分子内键参数采用Morse函数,角参数为简谐振动函数,二面角采用余弦函数形式,分子间非键作用函数形式为Buckingham势函数和库仑项(简称Boyd力场).Gee等12开发了三硝基三氨基苯(TATB)的力场,其分子内势函数形式和SB力场一样,但分子间势函数采用的是Lennard-Jones(12-6)势函数和库仑项(简称Gee力场),该力场在描述TATB晶体结构方面具有相当的稳定性和准确性.这些工作表明:用经验的力场函数模型可以较好地描述这一类含能材料的物理性质.但是已报道的力场均是针对单一分子开发的,而使用的函数形式也不一致,因此这些力场不具备可迁移性和在通用软件中的普适性.

为了扩大分子模拟方法在含能材料领域里的应用,需要建立具有可迁移性和普适性的分子力学力场.只有具有可迁移性,力场才可以用来预测不同条件下的物理性质.构建可迁移性力场的要点是同时拟合一组相似的分子,在不同的分子中根据相同的化学环境定义一致的原子类型,以获得在不同的条件下均可适用的参数.本文以TATB、RDX、HMX为对象,开发一个对此类材料分子适用的分子力学力场.为了普适性的要求,我们采用常用的力场函数形式,这样得到的力场可以在通用的分子模拟软件(如LAMMPS,13,14NAMD15和GROMACS16)上直接使用.

本文以几种常见的含能材料为研究对象,采用量子化学计算和分子动力学模拟等方法,开发了可迁移的力场.应用所得力场计算了分子和分子晶体的性质,并通过计算材料的p-V状态方程和机械性质对该力场进一步验证.

2 计算模型和方法

2.1 分子结构

图1 TATB、RDX和HMX的分子结构Fig.1 Molecular structures of TATB,RDX,and HMX

TATB分子是一个苯的六个氢原子分别被硝基和氨基取代而形成的包含分子内氢键的平面结构,RDX和HMX是含有硝胺基团的六元环和八元环.分子的结构见图1.TATB和RDX的稳定结构单一,但HMX有三种稳定的构象,分别为α-HMX、β-HMX和γ-HMX.这三种构象的差异在于四个硝基的相对位置不同:α-HMX的四个硝基位于八元环的同一侧;β-HMX的四个硝基中相邻的两对分别位于八元环的两侧;而γ-HMX的四个硝基中的一个位于八元环一侧,其余三个位于另一侧.

2.2 晶体结构

常温常压下TATB只有一种晶型,属于三斜晶系,每个晶胞有2个分子,为P1空间群.17RDX分子在常温常压下形成一种稳定的晶体,属于正交晶系,每个晶胞有8个分子,为Pbca空间群.18而HMX分子能形成四种晶型(α-HMX、β-HMX、γ-HMX、δ-HMX),其中γ-HMX为水合晶型,19这里不做研究.HMX在常温常压下稳定存在的是β型晶体,该晶体由β构象的HMX分子构成,每个晶胞2个分子,为单斜晶系P21/C空间群;20当温度升至375-377 K时,β-HMX晶体转换成α-HMX晶体,它由α构象构成,每个晶胞含有8个α-HMX,为正交晶系Fdd2空间群;21当温度升至433-437 K时,α-HMX晶体转换成δ-HMX晶体,它也由α构象构成,六方晶系P6122空间群,每个晶胞6个α-HMX分子.22γ构象的HMX分子不形成晶体.分子模拟所研究的五种晶体结构均引自文献,17,18,20-22建模使用Direct Force Field 7.1软件包.23超晶胞的组成如下:TATB含有3×3×4个单胞、RDX 含有2×2×2个单胞、β-HMX含有4×2×3个单胞、α-HMX含有2×1×4个单胞、δ-HMX含有3×3×1个单胞.

2.3 量子化学计算方法

量子化学计算采用B3LYP密度泛函方法和6-31G(d,p)基组24,25优化单分子结构、计算ESP26和Mulliken27电荷分布、构象能及分子的总能量对笛卡尔坐标的一阶和二阶导数.这些数据用来拟合力场的键参数和电荷参数.量子化学计算采用Gaussian 03软件包28实施.

2.4 力场势函数形式

采用的势函数包括成键项(分子内)和非键项(分子间)两部分.成键项包括键、角、二面角、面外键角和交叉项等.非键项包括静电相互作用(库仑形式)和范德华相互作用(LJ 12-6形式):

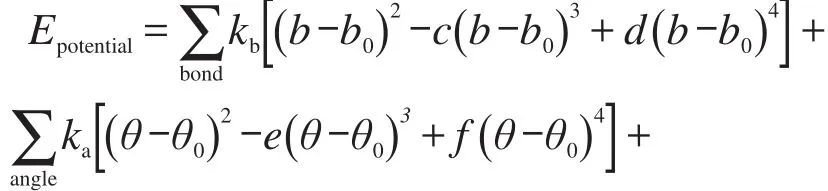
式中键参数部分kb、ka、kt、ko、kbb、kba分别为键伸缩、角伸缩、二面角扭转、面外键角、键键交叉项和键角交叉项的力常数,b为键长,θ为键角,φ为二面角,χ为面外键角,下标0表示相应的平衡值,c、d、e、f为系数;非键参数部分q为原子所带电荷数;rij是非键原子间的距离,r0ij是原子i和原子j的范德华相互作用半径,εij是原子i和原子j的相互作用势阱.

计算范德华相互作用时,不同原子间的Lennard-Jones参数采用Lorentz-Berthlot混合规则得到:

2.5 参数化方法

力场参数化是对分子内和分子间的参数分别优化并迭代的过程.为了保持力场参数的一致性,亚甲基和氨基的参数由我们以前推导的烷烃和胺类化合物的参数迁移得到.其它参数通过如下步骤得到:首先,确定并固定初始的电荷及范德华(VDW)参数,用最小二乘法拟合量子化学DFT计算的能量和能量导数确定分子内的键参数.电荷的初始参数用量子化学方法计算的Mulliken电荷,VDW的初始参数用OPLS力场29中相似的原子类型的非键参数.这样得到一个完整的力场后再用分子动力学模拟TATB、RDX和HMX晶体的晶胞性质、升华焓,并同实验数据对比优化电荷和VDW参数.上述过程循环迭代得到优化的力场参数.拟合过程使用Direct Force Field 7.1软件包.

2.6 分子动力学模拟

晶体的分子动力学模拟部分采用LAMMPS软件包,长程电荷作用采用Ewald/n方法,截断半径(cut off)为1.0 nm,时间步长1 fs,模拟时间2 ns,其中1 ns平衡,1 ns采样.采用恒温恒压系综(NPT),用Nose/Hoover控温控压方法,允许超晶胞的6个自由度(即3个边长和3个夹角)变化.

3 力场的建立和初步验证

3.1 原子类型

原子类型的定义仅仅与其附近的拓扑结构有关,根据原子在分子中所处的环境定义.原子类型的定义由三部分组成:中心原子的元素符号、中心原子连接其它不同原子的个数和备注项.例如:c_4h2,c表示中心原子为碳,4表示碳原子一共连4个其它原子,h2表示碳原子所连的4个其它原子中有两个是氢原子,所以c_4h2表示的是亚甲基上的碳原子类型.本文涉及到的原子类型有如下几种:苯环上连氨基的碳原子c_3an,苯环上连硝基的碳原子c_3ani,亚甲基上碳原子c_4h2,亚甲基氢原子h_1,氨基氢原子h_1n,氨基氮原子n_3h2,连硝基的氮原子n_3no,硝基上氮原子n_3o,硝基上氧原子o_1n.

3.2 电荷和VDW参数的确定

量子化学计算得到的ESP和Mulliken电荷见表1.从数据可以看出,对于相同的原子类型,Mulliken电荷比ESP电荷在不同的分子间更稳定.这是由于ESP电荷是通过拟合静电势得到的,拟合的结果受到采样方式的影响.26而根据波函数确定的Mulliken电荷更能准确地反映原子间电子密度的分布,因此我们选择Mulliken电荷作为初始电荷.

分子间相互作用本质上都是源于库仑力,可以用电荷-电荷、电荷-偶极、偶极-偶极以及包括四极矩和诱导偶极在内的库仑力来表达.而在力场方法中仅用到了位于原子上的电荷和VDW势、电荷分布和VDW势的结合用来表达分子间的相互作用.因此电荷分布可以在一个较宽的范围里采用,而分子间相互作用的其余部分由VDW势来表达.这一现象在OPLS29和COMPASS30的力场开发中已有报道.我们在优化电荷和VDW参数时也看到由Mulliken电荷推导出的电荷参数过分高估分子间相互作用,以致无法调整VDW参数来得到合理的晶格能.这是因为在形成分子晶体时分子间排列紧密,而这些分子都含强极性基团硝基,点电荷模型在近距离产生过强的静电作用.我们把点电荷参数统一地缩小至0.65倍,再调整VDW参数,得到了较好的效果.

表2列出优化的VDW势(即LJ 12-6函数)的参数和电荷参数.为了参数的完整性,从烷烃和胺类迁移的参数也一并列出.LJ 12-6参数按原子类型给出,不同原子类型间的相互作用采用组合规则(式2)计算.电荷用键增量(bond increment)30表达.对每个原子,其所带的电荷由式(3)计算得到,

式中j表示与i相连的所有其它原子.

3.3 分子性质

力场中的分子内参数是在分子间参数确定后通过拟合DFT计算的能量和能量导数确定的,完整的分子内参数在Supporting Information中给出.在得到参数以后,用分子力学方法对TATB、RDX和HMX分子进行结构优化并同量子化学计算结果对比来验证参数的可靠性.根据文献报道,B3LYP/6-31G(d,p)计算可以在实验精度范围里较好地再现分子的结构和构象能的实验值.24,25

表1 给定原子类型在不同分子里的ESP和Mulliken电荷Table 1 ESPand Mulliken charges for atom types in different molecules

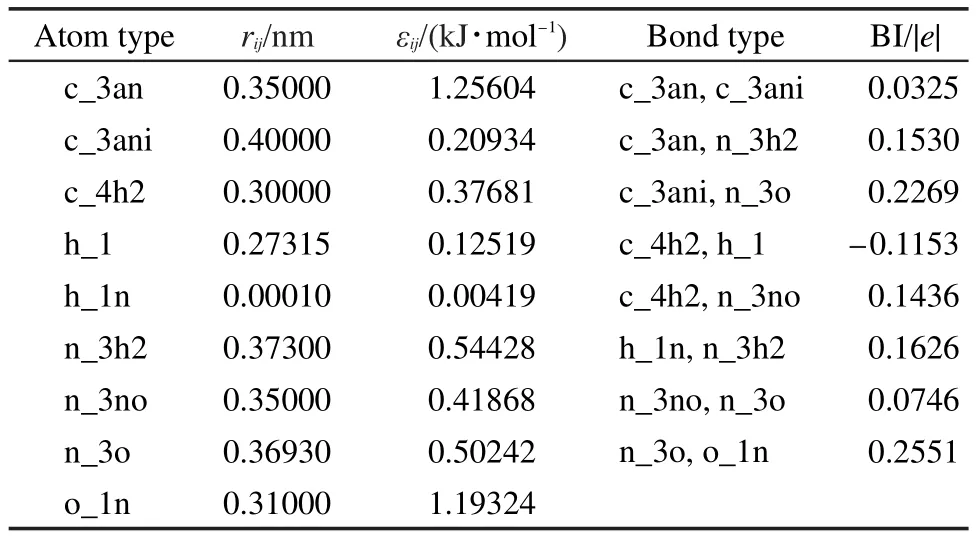
表2 范德华参数和电荷键增量参数Table 2 VDW and bond increment(BI)parameters of all the atom types

用优化参数计算所得到的键长、键角、二面角和基态简正振动频率等结果与量子化学结果对比如图2所示.力场优化的键长与量子化学优化的键长的均方差(MSD)小于0.0015 nm,键角的均方差小于3.7°,二面角均方差小于21.5°,振动频率均方差小于95 cm-1.二面角较大的均方差源于在HMX的三种构象中个别含H原子的二面角最大偏差达到40°左右.通过提高二面角的力常数可以将此偏差进一步减小,但刚性太大的二面角函数影响了力场在描述凝聚相物理性质时的表现.这一问题也反映了力场方法的局限性.

3.4 晶胞结构和升华焓

晶胞结构和升华焓是用来优化非键参数的指标.用优化的参数在实验温度21,22和常压下对TATB、RDX和HMX晶体进行模拟得到的晶胞参数、晶体密度及升华焓在表3列出,并与实验值17,18,20-22,31,32进行对比.

由结果可以看出,力场能准确描述这些晶体的结构性质,模拟的晶胞边长结果与实验值差别全部小于3.6%.晶胞夹角最大差异为TATB的β角,与实验测量值相差4.1°,其余夹角偏差全部小于2.3°.在室温下得到的晶体密度与实验值相吻合.TATB的密度为1.923 g·cm-3,比实验值偏低0.72%.RDX晶体密度的计算结果为1.801 g·cm-3,比实验值偏低0.28%.β-HMX的密度比实验值低1.7%.总的来说,这些数据优于文献中报道的力场8,11,33得到的结果,只有Gee力场12计算得到了和实验完全一致的数据,是例外.对于模拟温度高于常温的两种材料α-HMX和δ-HMX,密度相比于实验值较大,分别是偏小5.6%和3.6%.

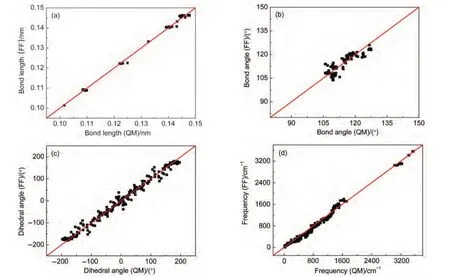
图2 用力场(FF)和量子化学(QM)方法优化得到的分子键长(a),键角(b),二面角(c)及振动频率(d)的对比Fig.2 Comparisons of optimized bond lengths(a),bond angles(b),dihedral angles(c),and vibrational frequencies(d)between quantum chemistry(QM)and force field(FF)methods

表3 晶体的晶胞参数、密度和升华焓(ΔHsub)Table 3 Crystal cell parameters,densities,heat of sublimation(ΔHsub)

表3中升华焓ΔHsub按照如下公式进行近似计算:

上式中,Einter是体系的内聚能,即分子间相互作用;R为摩尔气体常数,8.314 J·K-1·mol-1;T为温度.α-HMX和δ-HMX的升华焓缺乏准确的实验测量值.TATB、RDX和β-HMX的升华焓计算结果和实验值相比偏差分别为2.9%、1.2%和-4.1%.而之前的力场预测的误差分别是TATB:-22.7%(Gee34),RDX:-11.4%(SRT8),-10.9%(Boyd11)和β-HMX:3.0%(SB33).

4 晶体的状态方程和机械性质

我们通过计算晶体的状态方程和机械性质进一步验证了得到的力场的可靠性.这些性质的计算对优化参数有指导意义,但没有直接用来优化参数,因此提供了更为严格的测试条件.

含能材料晶体在高压下的热力学状态方程是描述该类材料的一个重要性质.我们计算了298 K下几种含能材料分子晶体的压力-体积(p-V)曲线.图3是计算得到的TATB、RDX和β-HMX的p-V曲线及其和文献35-39的对比.其中RDX在大于4 GPa的压力下会发生相变,因此只计算了小于4 GPa的情况.从图中可以看出,TATB的预测结果和实验值基本一致;而RDX在高压下和实验值稍有偏差,高估体积约0.9%;β-HMX的结果和实验值相比在低压下(0.5 GPa)体积偏小0.8%左右.总的来说,这些数据优于文献中报道的计算值.

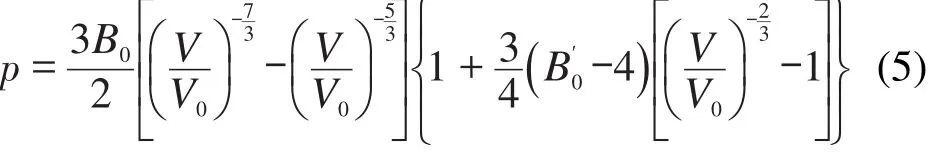
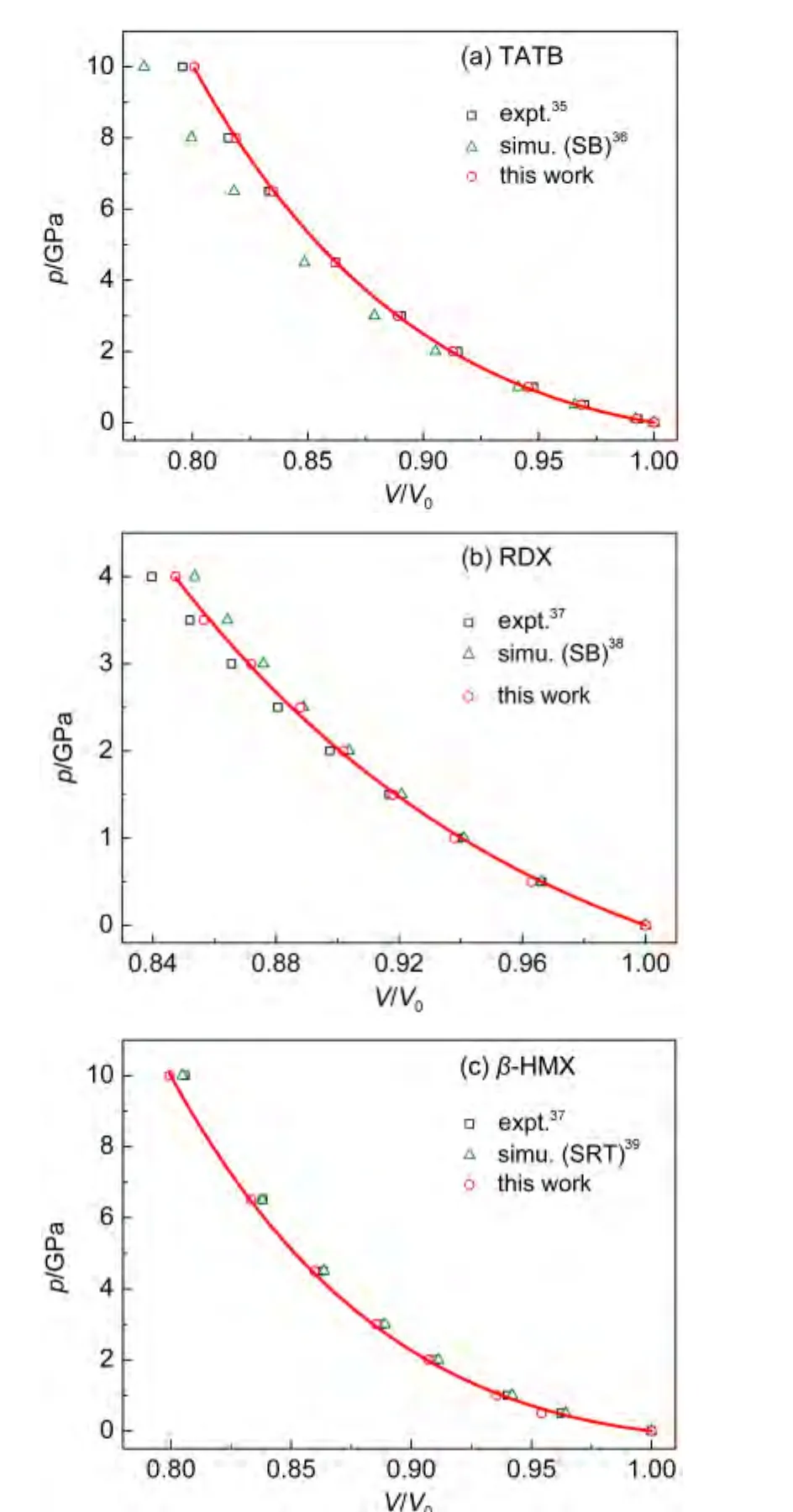
图3 TATB、RDX和β-HMX在298 K下的p-V曲线Fig.3 p-V curves of TATB,RDX,and β-HMX at 298 K

表4 298 K下晶体的体积模量(B0)及其一阶导数(B′0)的理论计算值Table 4 Calculated bulk modulus(B0)and their first derivatives(B′0)at 298 K

体积模量及其对压力的一阶导数利用三阶Birch-Murnaghan公式拟合p-V曲线得到:式中B0为晶体的体积模量,B'0为体积模量对压力的一阶导数,p为压力,V为该压力下材料的体积,V0为初始条件下材料的体积.表4为拟合三种材料的p-V曲线所得的体积模量的计算结果与文献报道结果35-39的对比.由表中数据可以看出,该力场在预测材料机械性质上有着较好的表现,所得结果和实验值以及其它理论计算值相比都比较接近.

5 结论

报道了一个适用于TATB、RDX和HMX含能材料的,可以在通用软件中使用的分子力学力场,并通过计算分子和分子晶体的物理性质验证了该力场.验证结果显示该力场可以较好地重现量子化学DFT预测的分子结构、构象和振动频率,得到和实验值基本一致的(包括HMX在不同温度下的三种晶型)的晶胞参数、密度和升华焓.扩展到预测TATB、RDX和β-HMX分子晶体的等温p-V曲线、体积模量及其对压力的一阶导也得到与文献报道的计算和实验数据一致的结果.这些结果显示了用经验的力场函数可以在较大温度压力范围内描述含能材料的物理性质.和文献中已发表的力场对比,由于采用了统一的力场函数形式和原子类型描述含硝基、氨基的芳香或非芳香性环状化合物,本文提出的力场具有更好的可迁移性和普适性,为我们进一步深入研究这些含能材料的物理性质提供了可能,也为我们进一步开发粗粒化力场、在更大尺度上研究这一类材料打下了基础.

Supporting Information: The valence parameters of the force field have been included.This information is available free of charge via the internet at http://www.whxb.pku.edu.cn.

(1)Gee,R.H.;Maiti,A.;Bastea,S.;Fried,L.E.Macromolecules 2007,40,3422.doi:10.1021/ma0702501

(2) Maiti,A.;Gee,R.H.;Hoffman,D.M.;Fried,L.E.J.Appl.Phys.2008,103,053504.doi:10.1063/1.2838319

(3) Xiao,J.;Huang,H.;Li,J.;Zhang,H.;Zhu,W.;Xiao,H.J.Mater.Sci.2008,43,5685.doi:10.1007/s10853-008-2704-0

(4) Xu,X.;Xiao,J.;Huang,H.;Li,J.;Xiao,H.J.Hazard.Mater.2010,175,423.doi:10.1016/j.jhazmat.2009.10.023

(5) Zhou,Y.;Long,X.;Wei,X.J.Mol.Model.2011,17,3015.doi:10.1007/s00894-011-0977-8

(6) Huang,Y.C.;Hu,Y.J.;Xiao,J.J.;Yin,K.L.;Xiao,H.M.Acta Phys.-Chim.Sin.2005,21,425.[黄玉成,胡应杰,肖继军,殷开梁,肖鹤鸣.物理化学学报,2005,21,425.]doi:10.3866/PKU.WHXB20050416

(7) Xiao,J.J.;Gu,C.G.;Fang,G.Y.;Zhu,W.;Xiao,H.M.Acta Chim.Sin.2005,63,439.[肖继军,谷成刚,方国勇,朱 伟,肖鹤鸣.化学学报,2005,63,439.]

(8) Sorescu,D.C.;Rice,B.M.;Thompson,D.L.J.Phys.Chem.B 1997,101,798.doi:10.1021/jp9624865

(9) Sorescu,D.C.;Rice,B.M.;Thompson,D.L.J.Phys.Chem.B 1998,102,6692.doi:10.1021/jp981661+

(10)Smith,G.D.;Bharadwaj,R.K.J.Phys.Chem.B 1999,103,3570.doi:10.1021/jp984599p

(11) Boyd,S.;Gravelle,M.;Politzer,P.J.Chem.Phys.2006,124,104508.doi:10.1063/1.2176621

(12) Gee,R.H.;Roszak,S.;Balasubramanian,K.;Fried,L.E.J.Chem.Phys.2004,120,7059.doi:10.1063/1.1676120

(13) Plimpton,S.J.Comput.Phys.1995,117,1.doi:10.1006/jcph.1995.1039

(14)Plimpton,S.LAMMPS:Large-ScaleAtomic/Molecular Massively Parallel Simulator.http://lammps.sandia.gov.

(15) Phillips,J.C.;Braun,R.;Wang,W.;Gumbart,J.;Tajkhorshid,E.;Villa,E.;Chipot,C.;Skeel,R.D.;Kale,L.;Schulten,K.J.Comput.Chem.2005,26,1781.

(16) Van Der Spoel,D.;Lindahl,E.;Hess,B.;Groenhof,G.;Mark,A.E.;Berendsen,H.J.J.Comput.Chem.2005,26,1701.

(17) Cady,H.H.;Larson,A.C.Acta Crystallogr.1965,18,485.doi:10.1107/S0365110X6500107X

(18) Choi,C.;Prince,E.Acta Crystallogr.Sect.B 1972,28,2857.doi:10.1107/S0567740872007046

(19) Cady,H.H.;Smith,L.C.Los Alamos Scientific Laboratory Report LAMS-2652 TID-4500;LosAlamos National Laboratory:LosAlamos,NM,1961.

(20) Choi,C.S.;Boutin,H.P.Acta Crystallogr.Sect.B 1970,26,1235.doi:10.1107/S0567740870003941

(21) Cady,H.H.;Larson,A.C.;Cromer,D.T.Acta Crystallogr.1963,16,617.doi:10.1107/S0365110X63001651

(22) Cobbledick,R.;Small,R.Acta Crystallogr.Sect.B 1974,30,1918.doi:10.1107/S056774087400611X

(23) Direct Force Field,7.1;Aeon Technology Inc.:San Diego,CA,USA,2012.

(24) Rice,B.M.;Chabalowski,C.F.J.Phys.Chem.A 1997,101,8720.doi:10.1021/jp972062q

(25)Riley,K.E.;Op't Holt,B.T.;Merz,K.M.J.Chem.Theory Comput.2007,3,407.doi:10.1021/ct600185a

(26)Breneman,C.M.;Wiberg,K.B.J.Comput.Chem.1990,11,361.

(27) Mulliken,R.S.J.Chem.Phys.1955,23,1833.doi:10.1063/1.1740588

(28) Frisch,M.;Trucks,G.;Schlegel,H.;et al.Gaussian 03,Revision C.02;Gaussian Inc.:Wallingford,CT,2004.

(29)Jorgensen,W.L.;Maxwell,D.S.;Tirado-Rives,J.J.Am.Chem.Soc.1996,118,11225.doi:10.1021/ja9621760

(30) Sun,H.J.Phys.Chem.B 1998,102,7338.doi:10.1021/jp980939v

(31) Rosen,J.M.;Dickinson,C.J.Chem.Eng.Data 1969,14,120.doi:10.1021/je60040a044

(32) Taylor,J.W.;Crookes,R.J.J.Chem.Soc.Faraday Trans.1976,72,723.doi:10.1039/f19767200723

(33) Bedrov,D.;Ayyagari,C.;Smith,G.D.;Sewell,T.D.;Menikoff,R.;Zaug,J.M.J.Comput.Aided Mater.Des.2001,8,77.doi:10.1023/A:1020046817543

(34) Rai,N.;Bhatt,D.;Siepmann,J.I.;Fried,L.E.J.Chem.Phys.2008,129,194510.doi:10.1063/1.3006054

(35) Stevens,L.L.;Velisavljevic,N.;Hooks,D.E.;Dattelbaum,D.M.Propellants Explos.Pyrotech.2008,33,286.doi:10.1002/prep.v33:4

(36) Bedrov,D.;Borodin,O.;Smith,G.D.;Sewell,T.D.;Dattelbaum,D.M.;Stevens,L.L.J.Chem.Phys.2009,131,224703.doi:10.1063/1.3264972

(37) Olinger,B.;Roof,B.;Cady,H.In Proceedings of International Symposium on High Dynamic Pressures;Commissariat a l′EnergieAtomique:Paris,France,1978;p 3.

(38) Zheng,L.;Thompson,D.L.J.Chem.Phys.2006,125,084505.doi:10.1063/1.2238860

(39)Sorescu,D.C.;Rice,B.M.;Thompson,D.L.J.Phys.Chem.B 1999,103,6783.doi:10.1021/jp991202o