大型管件管端过弯矫圆三步法控制策略

展培培，赵 军，李 平，尚京华

(1.燕山大学先进锻压成形技术与科学教育部重点实验室，河北秦皇岛 066004;2.中国第一重型机械股份公司重型技术装备基础科学研究院，辽宁大连 116113;3.燕山大学里仁学院，河北秦皇岛 066004)

近年来，随着我国对油气输送、风电、核电等基础设施的投入日益增大，其相关产业中所需的钢管、弯头、三通等大型管件的产量也在逐步增加，进而对各类管件的质量要求也越来越严格［1-2］.成品管件的管体椭圆度和管端椭圆度都是衡量管件品质的重要指标.美国制管协会API Spec 5L标准［3］规定，管件制品的管体椭圆度不应超过钢管公称直径的1.0%，而对于管端，若其椭圆度超标后，将直接导致在车削管端焊接坡口时出现困难，使其尺寸不达标，进而影响具体使用过程中管件间的焊接连接工艺，因此管端椭圆度要求较管体更为严格.

相关研究表明大型直缝焊管生产过程中的扩径工艺对管体的椭圆度有一定的矫正作用［4-7］，并且在此基础上殷璟等［8-10］分析了缩径工艺，并从实验上证实了该工艺具有矫圆效果理想，操作简单等优点.潘鑫［11］通过数值模拟方法提出了焊管的整圆定径工艺，即通过使用两瓣模对焊管施压使其周长产生0.5%的永久变形，从而改变管坯椭圆度.贺幼良［12］和王关荣［13］分别研究了适用于压力容器的外抱式和内撑式整圆工艺，同时给出了合适的模具参数尺寸和工艺参数.然而上述的矫圆工艺均在矫正椭圆度的同时改变了管件的截面周长尺寸，因此限制了其广泛应用.当前，大型管件生产厂家使用的较为广泛的矫圆方法均是使用一对小曲率圆弧瓣模压制管坯端部，使其产生塑性变形，从而矫正椭圆度误差(简称为管端过弯矫圆［14］).该工艺具有操作简单，效率高等优点，并且能同时使用同一组模具完成多种规格管坯的矫圆，节约了生产成本.然而该工艺主要停留在依赖操作人员的经验阶段，通过反复测量、反复压制管坯的方式，从而严重地影响了矫圆效率，因此，生产厂家急需有效的控制策略指导其生产过程.先前，本文作者建立了两步法过弯矫圆控制策略［15］，但是该控制策略需要在实际应用前首先完成管坯材料性能试验，从而限制其应用.为此，本文建立了不依赖于管坯材料性能参数的三步法过弯矫圆控制策略.

1 管端过弯矫圆概述

管端过弯矫圆是一种基于弹塑性小变形的矫圆工艺，矫圆前后被矫对象截面几何中性层周长近似不变.由圣维南原理可知，管坯沿其轴向方向可分为三个主要区域，即与模具接触的管端主变形区，其长度用L表示，受变形影响的牵连变形区，以及未变形区，如图1所示.

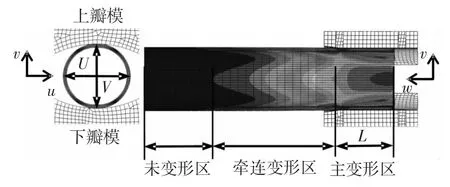
图1 管端过弯矫圆示意图

主变形区的变形过程示意图如图2所示.变形过程中，A点及其临近区域中性层曲率不断增大，产生同向弯曲，B点及其临近区域中性层曲率不断减小，产生反向弯曲.考虑到弯曲回弹的影响，初始纵向椭圆必须矫至横向椭圆，卸载后管坯截面才能成为圆形，因此称此工艺为过弯矫圆工艺.

图2 管端模压式过弯矫圆示意图

2 过弯矫圆等价关系

为降低分析难度，首先通过实验方法分析待矫圆管坯的矫圆过程与圆截面管坯压扁过程，确定两个成形过程的工艺参数与卸载后椭圆度之间的相关关系，进而寻求将压扁过程的规律用于过弯矫圆过程中的可能性.

实验在WDD-LCT-150型电子拉扭组合多功能实验机上完成，位移控制精度为0.01 mm.管坯的测量采用便携式三坐标测量仪完成，其测量精度为0.01 mm.管坯试件采用两种不同规格的直管，相关参数如表1所示，经测量圆截面直管坯具有一定的初始椭圆度，其值的范围小于0.1%.根据过弯矫圆工艺的特点，本文所涉及的实验均采用同一套模具.模具模腔半径的设计原则为确保管坯在矫圆过程中充分进入塑性变形的同时不发生管坯局部畸变.实验模具模腔截面圆弧半径Rd为120 mm.为降低矫圆瓣模端部附近对管坯的应力集中，瓣模的一端被加工成锥角为7°长度为20 mm的倒角.实验装置和管坯试样如图3所示.

表1 管坯试样几何参数

图3 过弯矫圆实验装置

制定实验方案如下:第一步，压扁过程，以确定的压下量h和主变形区长度L将管端压成椭圆，记录卸载后的管端椭圆度;第二步，矫圆过程，将第一步卸载后具有一定椭圆度管坯绕其轴线旋转90°，并以与第一步相同的实验装置，相同的方式和相同的压下量压制管坯，记录管端最后的残余椭圆度.

椭圆度［3］的定义为

式中，U、V分别为图1所示的以外表层度量的管端u方向轴长和v方向轴长，D为管坯的公称外径.

不同规格的管坯在不同压下量，不同变形区长度条件下的实验结果如表2所示.其中相对压下量的定义为

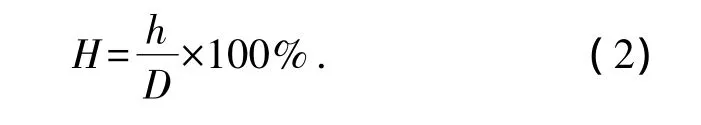
由实验结果可知，管坯残余椭圆度最大为0.31%，最小为0.19%，都远小于1%的标准要求.但是管坯最终的椭圆度都为正值，且在一小范围内波动，表明材料反复加载时的包辛格效应和材料性能的波动是造成该现象的主要原因.

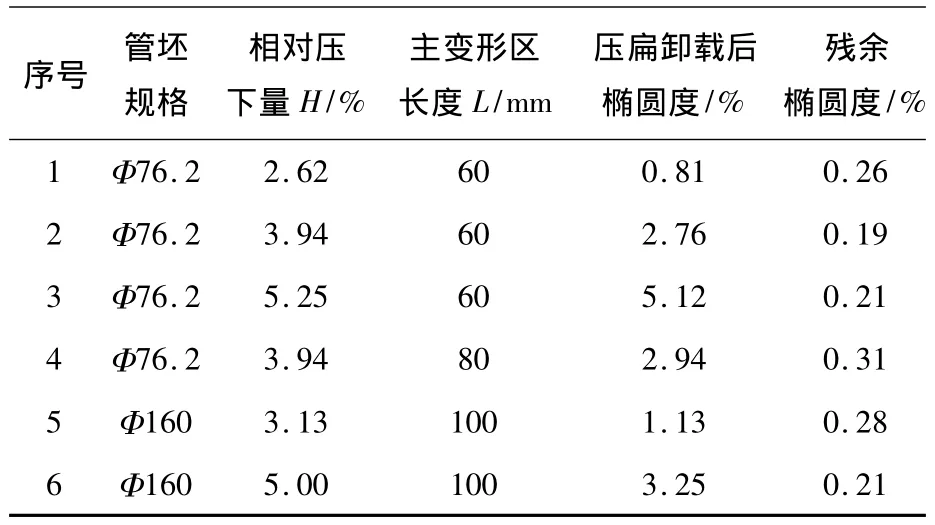
表2 过弯矫圆等价关系实验结果

实验结果表明:在工程应用的精度范围内，管端的矫圆过程等价于压扁过程，所谓等价是指可以用圆截面管坯经模压方式压成待矫圆管坯椭圆度所需压下量作为过弯矫圆的压下量对待矫圆管坯进行矫圆处理.

3 管端压扁弹复规律

分析同批次、同型号的不同管坯管端压扁过程的弹复规律以及同一个管坯在多次的被压扁时的弹复规律是否具有一致性将从根本上影响控制策略.因此，本文从两个角度在实验上分析了管端压扁规律，一种是采用同批次、同型号的多个管坯，另外一种是只采用一个管坯.

在不同主变形区长度条件下，不同规格管坯的压扁过程中卸载后管端椭圆度与相对压下量之间的关系曲线如图4所示.实验装置和管坯规格与上述等价关系实验相同.其中Φ76.2 mm管坯的弹复规律是采用同批次、不同管件在不同主变形区长度的条件下分别使用不同的压下量时被压扁而获得，而Φ160 mm管坯的弹复规律曲线是用同一个管件在使用不同压下量时被压扁而获得.

图4 卸载后椭圆度与相对压下量关系曲线

对同一个管件采用不同的压下量进行压制时，将管坯的压下量定义为:以首次预压上瓣模接触管坯时为压下行程零点，以加载后上瓣模相对于压下行程零点的偏移量为各压制步的压下量h，如图5所示.

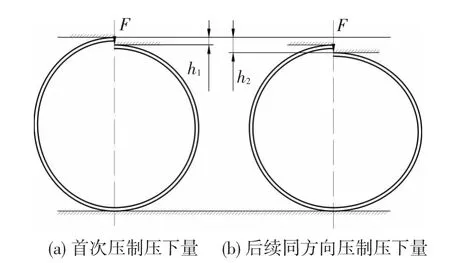
图5 压下量定义示意图

由图4可知，相对压下量较小时，管坯处于弹性变形范围内，卸载后管端椭圆度不变，而随着压下量逐渐增大，卸载后管端椭圆度递增.

由椭圆度标准［3］可知，待矫管坯的初始椭圆度均大于1%，因此被矫管坯在矫圆前后的管端椭圆度变化量应大于1%.线性拟合塑性变形阶段卸载后椭圆度大于1%的数据，线性拟合的相关系数R值均大于0.99.由此可以表明在被矫管坯的实际椭圆度变形量范围内和工程允许的精度范围内完全可以使用线性关系来制定过弯矫圆的工艺参数.而在塑性变形阶段卸载后椭圆度小于1%的范围内的实验点距离所拟合的直线较远.考虑是因为管坯刚进入了塑性屈服，而钢铁材料的塑性屈服平台导致了该阶段变形的不稳定性，以致该范围内的实验点向所拟合直线的上方偏离.

比较图4所示主变形区长度不同的Φ76.2 mm管坯结果可知，变形区长度为60 mm时的相对压下量与卸载后椭圆度之间线性关系中的斜率小于主变形区长度为70 mm时，而主变形区长度为40 mm时的斜率又明显小于60 mm时，即随着变形区长度的增大，其线性关系的斜率也逐步增大.

4 三步法过弯矫圆控制策略

合理的工艺控制策略是提高生产效率的主要手段之一.根据上述管端压扁过程弹复规律，即在椭圆度变化量大于1%时卸载后椭圆度与相对压下量的线性关系以及过弯矫圆等价关系，建立了三步法过弯矫圆控制策略.

对一批同型号的管件，首先通过对首支管件进行两次预压而得到管坯压扁过程的弹复规律，即上述线性关系的数学表达式，然后根据该弹复规律计算出首支管件矫圆所需的压下量，完成其矫圆过程.而在后续的管件矫圆时即可直接根据所得到的弹复规律计算出待矫管坯矫圆所需的最佳压下量.

4.1 三步法控制策略的基本步骤

三步法控制策略示意图如图6所示.其中直线1的意义为管端压扁过程的弹复规律，直线2的意义为初始椭圆度为δ0的管坯管端矫圆过程的弹复规律.根据上述压扁过程与矫圆过程的等价关系可知，两条直线的起始点横坐标和斜率相等.

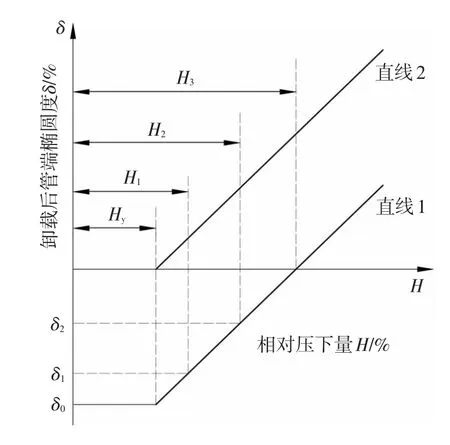
图6 三步法控制策略示意图

三步法控制策略的具体步骤如下:

第一步，以一定的相对压下量H1沿首支管坯的长轴方向压制管端，同时保证管端卸载后椭圆度与初始椭圆度相比的变化量大于1%，记录卸载后管端椭圆度δ1;

第二步，同第一步，以一定的相对压下量H2继续预压管坯端部，压制方向与第一步相同，同样记录卸载后管端椭圆度δ2;

第三步，通过两次预压结果计算管端压扁过程和椭圆度为δ0的管端矫圆过程的弹复规律，即直线1和直线2的方程;

第四步，利用第三步计算结果，计算首支管矫圆所需压下量，即终压所需相对压下量H3，并对管坯进行第三次压制，完成矫圆过程，同时修正弹复规律.

管坯经过第一、二步的压制后存在两种情况，一种为椭圆度方向与初始椭圆度方向相同，即弹复后长轴方向仍为初始状态的长轴方向，另一种情况为椭圆度方向与初始椭圆度方向相反.相同时，第三步的矫圆压下量根据图5所示定义，相反时，将管坯视为待矫圆新管坯，并根据管端椭圆度直接预测矫圆压下量.

第五步，利用上述得到到弹复规律直接预测后续管坯矫圆所需最佳压下量并对其进行矫圆.

采用三步法控制策略矫圆过程中，管端的主变形区长度L保持不变.第三次矫圆相对压下量H3的计算方式如下:

设管端压扁过程弹复规律的直线方程，即直线1的方程为

式中k为斜率，Hy为横轴截距.则直线2的方程可表述为

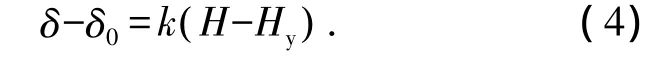
如图 6 所示，点(H1，δ1)、(H2，δ2)在直线 2上，将两点坐标带入式(4)即可解得

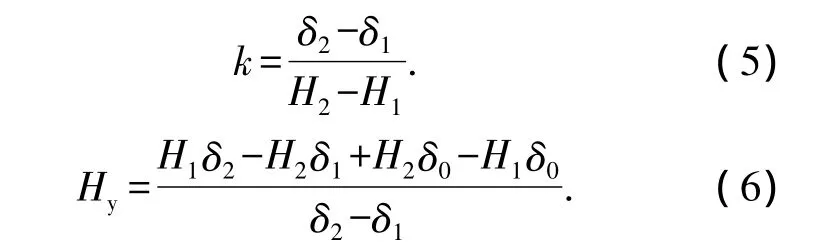
从而可得到管端压扁过程的弹复规律，即式(3).首支管矫圆所需压下量分两种情况确定，当经过前两步压制后管端椭圆度方向与初始椭圆度方向相同时，终压所需变形量H3为

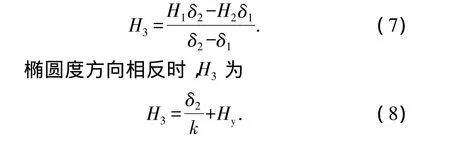
4.2 首支管坯预压压下量的确定

由上述的控制策略可知，合理地选择预压压下量是准确获得压扁过程弹复规律的关键.根据过弯矫圆的特点，制定首次预压压下量h1的流程图如图7所示.首先采用初始压下量ha沿长轴方向压制管坯端部，ha的大小以加载后管坯端部截面椭圆度近似等于0为准，即

式中U0为管端初始状态图1所示的u方向轴长，V0为管端初始状态v方向轴长.待测得卸载后管端椭圆度 δa后，判断的值是否大于1%，若大于则完成首次预压过程，若小于则判断管坯是否进入塑性变形，即是否等于0，若等于0则用2ha继续试压管坯端部，若不等于0则以修正后的压下量hm压制管坯端部，进而得到卸载后管端椭圆度δm.hm的表述为

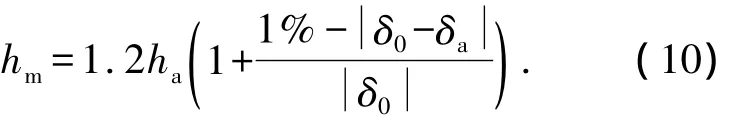
为了简化第二次预压压下量的制定规程，规定第二次预压时的压下量为

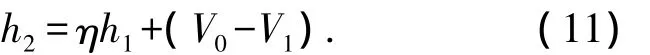
式中η∈(1-1.5)为常系数，V1为管端第一次预压卸载后v方向轴长.

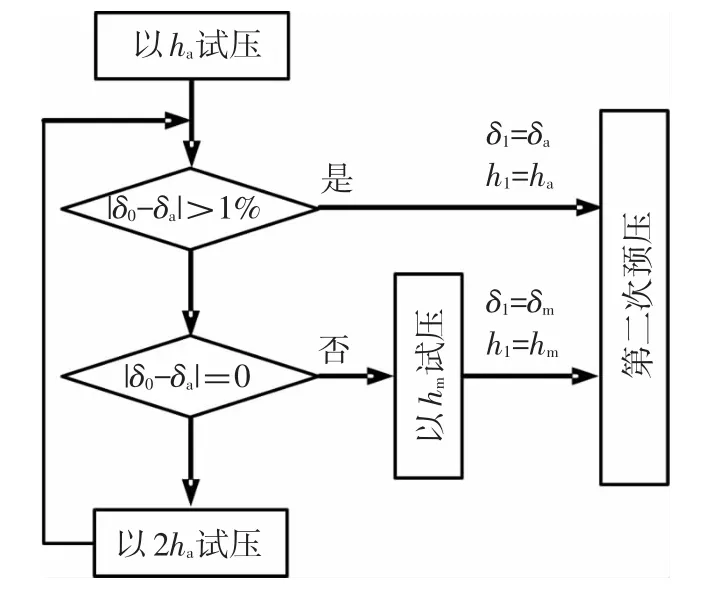
图7 预压压下量的确定流程图

4.3 后续管坯矫圆最佳压下量的预测及压扁弹复规律的修正

待完成了首支管坯的矫圆后，对于后续初始椭圆度为δ'的管坯可根据所得到的弹复规律直接预测最佳矫圆压下量H'，即

然而，由于管坯材料性能的波动及操作误差的影响，利用式(12)给出的最佳矫圆压下量并不能保证管坯矫圆后椭圆度刚好为0.而且若管坯材料性能差异较大时，甚至可能存在一次矫圆不达标现象.此种情况时可根据Hy的值和首次压制结果重新计算直线1的表达式，以计算该管坯的矫圆压下量对其进行二次矫正.对于矫圆后椭圆度达标管件，则根据具体矫圆结果对弹复规律中的k和Hy进行修正.

假定以最佳矫圆压下量Hi对初始椭圆度为δi的第i个管坯矫圆后残余椭圆度为根据图5所示，点)在直线1上.结合首支管三次压制的结果即可根据最小二乘法对直线1的方程参数进行修正.

4.4 控制策略的实验验证

根据上述三步法矫圆控制策略，选取了三个初始椭圆度不同的Φ160 mm管坯(表1)对其进行了实验验证，结果如表3所示.管坯的初始椭圆度通过使用压力机径向压制管坯而获得.矫圆实验的管坯主变形区长度L均为100 mm.实验装置同上.表3中1号管坯为矫圆控制策略的首支管坯，矫圆分三步完成，前两次为预压，首次预压相对压下量根据式(9)和式(2)确定，第二次预压的相对压下量根据式(11)确定，且常系数η取1.2.2号及3号管坯均采用的根据1号管坯压制结果所得到的弹复规律直接预测的矫圆最佳相对压下量矫圆.

表3 直管管端控制策略实验结果

为了验证该控制策略是否适用于异型管件的管端矫圆，选取了三个主管管端初始椭圆度不同的等径三通对控制策略进行进一步验证，结果如表4所示.管坯几何尺寸如表一所示，三通的初始椭圆度由成形后的蠕变引起.考虑到三通主管管端直壁段较短，主变形区长度选择20 mm.同样表4中1号管坯为矫圆控制策略的首支管坯.由于管坯初始椭圆度较小当试压相对压下量为3Ha时管坯才进入塑性屈服，且卸载弹复后椭圆度差量 δ0-δa小于1%.因此采用修正后的压下量hm作为管坯的首次压制压下量.首次压制后管坯椭圆度已经符合标准要求，但是为获得管坯的卸载规律，将初始管坯以式(11)和式(2)确定的相对压下量 (η=1)进行了第二次压制，并根据两次的压制结果重新将管坯矫圆.

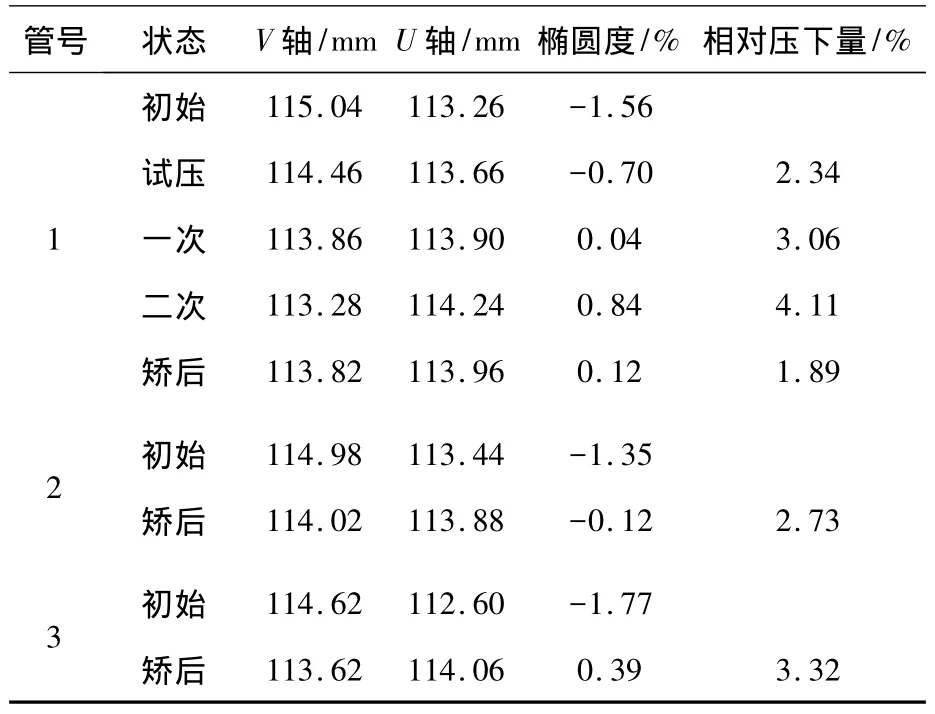
表4 三通主管管端控制策略实验结果

由两种不同形状管坯的实验结果可知，首支管件的最终椭圆度分别为0.20%和0.12%，而后续管件的管端矫圆过程均由一次压制完成，并且矫圆后的最终椭圆度均不大于0.5%.管坯的残余椭圆度同时出现了正值与负值，表明管坯材料性能的波动对最终的矫圆结果有一定影响，但是最终的结果均远小于标准要求.由此证实了本文所建立的过弯矫圆三步法控制策略可以准确可靠地为过弯矫圆工艺制定最佳工艺参数，从而为后续的过弯矫圆智能化控制策略奠定了基础.并且，最终的实验结果还间接的证明了本文所采用的过弯矫圆等价关系在工程应用意义上的合理性.

根据图6所示相关关系和过弯矫圆等价关系将表3和表4中的矫圆过程实验数据，即相对压下量和椭圆度实验数据，转换成相应的圆截面管坯压扁过程弹复规律曲线上的数据(用矫圆时管坯的残余椭圆度减去初始椭圆度的所得值代替圆截面管坯在相同相对压下量条件下变形后的椭圆度大小)，并进行进行最小二乘法直线拟合处理，得到的线性规律如图8所示.

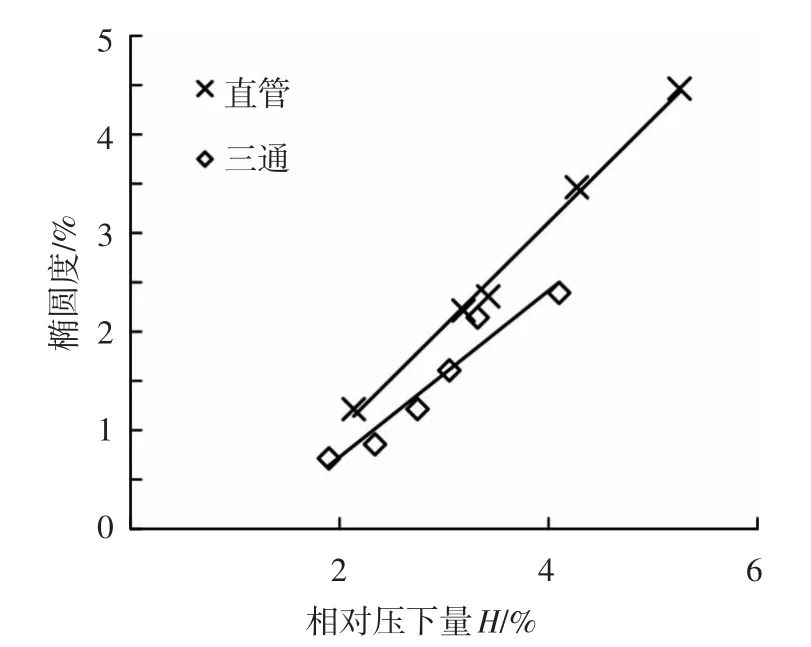
图8 矫圆数据直线拟合结果

可知，拟合后最终结果较为理想，实验点基本在拟合直线附近，由此再次证明了采用线性关系制定过弯矫圆工艺参数的合理性.

5 结论

1)管端矫圆过程与管端压扁过程存在等价关系.所谓等价，是指在工程精度允许的范围内当管坯材质、壁厚、截面几何中性层周长、以及模压方式均相同时，矫圆所需的压下量等于圆截面管坯压成待矫管坯椭圆度所需的压下量.

2)在工程精度的许可范围内，管端压扁过程中当管端的椭圆度变化量在矫圆的变形量范围内时，即椭圆度变化量大于1%时，可以直接采用卸载后管端椭圆度与相对压下量之间的线性关系代替二者之间的真实关系.

3)根据过弯矫圆等价关系和压扁过程的弹复规律建立了管端过弯矫圆三步法控制策略，即对于待矫的同批管件，首先通过三步压制首支管件获得弹复规律，然后根据弹复规律直接预测后续管件的最佳矫圆压下量.

4)利用直管件和三通管件对三步法控制策略进行了验证，实验结果表明，可以将管端最终的残余椭圆度控制在0.5%以内.

［1］杨秀琴.关于我国钢管行业发展战略的思考(上)［J］.钢管，2006，35(1):12-18.YANG Xiuqin.Proposal for Development of Domestic Steel Tube making industry(PartⅠ)［J］.Steel Pipe，2006，35(1):12-18.

［2］杨秀琴.关于我国钢管行业发展战略的思考(下)［J］.钢管，2006，35(2):10-14.YANG Xiuqin.Proposal for Development of Domestic Steel Tube making industry(PartⅡ)［J］.Steel Pipe，2006，35(2):10-14.

［3］ANSI/API Specification 5L，forty-foruth edition，ISO 3183:2007， Specification forline pipe， ［S］.Washington DC:2009.

［4］殷璟，赵军，屈晓阳，等.大型管件扩径矫圆弹复分析［J］.机械工程学报，2011，47(12):32-42.YIN Jing， ZHAO Jun， QU Xiaoyang， etal.Springback Analysis of Expanding and Setting Round for Large Diameter Pipe［J］.Chinese Journal of Mechanical Engineering，2011，47(12):32-42.

［5］范利锋，高颖，李强.大口径直缝焊管机械扩径工艺的研究进展［J］.重型机械，2011，(5):1-5.FAN Lifeng，GAO Ying，LI Qiang.Research progress of mechanical expanding technology for large diameter welded pipe［J］.Heavy Machinery，2011，(5):1-5.

［6］KARRECH A，SEIBI A.Analytical model for the expansion of tubes under tension［J］.Journal of Materials Processing Technology，2010，210(2):356-362.

［7］ZHAO Jun，YIN Jing，MA Rui，et al.Springback equation of smallcurvature plane bending［J］.SCIENCE CHINA:Technological Sciences，2011 54(9):2386-2396.

［8］殷璟，赵军，孙红磊，等.大型管件的模压式精确缩径矫圆［J］.光学精密工程，2011，19(9):2072-2078.YIN Jing，ZHAO Jun，SUN Honglei，et al.Precise compression and setting round by mold for large pipes［J］.Optics and Precision Engineering，2011，19(9):2072-2078.

［9］于海平，李春峰.管件电磁成形数值模拟方法及缩径变形分析［J］.材料科学与工艺，2004，12(5):536-539.YU Haiping，LI Chunfeng.Numerical modeling methods of electromagnetic forming and analysis of electromagnetic tube-compression［J］.Materials science ＆technology，2004，12(5):536-539.

［10］黄金龙，曾志新，陈举聪，等.微小型轴向内沟槽铜管缩径缺陷实验研究［J］.材料科学与工艺，2012，20(4):116-120.HUANG Jinlong，ZENG Zhixin，CHEN Jucong，et al.Forming defects of axial inner micro-grooved copper tubethrough two-split dies rotary swaging process［J］.Materials science＆ technology，2012，20(4):116-120.

［11］潘鑫，陈鹏，钱勇.大口径直缝焊管整圆定径工艺过程的数值模拟［J］.钢管，2009 38(5):70-73.PAN Xin，CHEN Peng，QIAN Yong.Numerical simulation of rounding-sizing process of large-sized straight welded pipe［J］.Steel pipe，2009 38(5):70-73.

［12］贺幼良，乔进先，贾春德.焊管整圆工艺研究［J］.焊管，1998，21(3):20-23.HE Youliang，QIAO Jinxian，JIA Chunde.The Circularization Technique for Welded Pipes［J］.Welded pipe and tube，1998，21(3):20-23.

［13］王关荣.压力容器整圆模的设计和应用［J］.压力容器，1991，6:40-44.WANG Guanrong.The design and application of rounding moulds for pressure vessels［J］.Pressure vessel Technology，1991，6:40-44.

［14］赵军，展培培，曹宏强.管线钢管内胀过弯矫圆最佳工艺参数预测［J］.材料科学与工艺，2010，18(1):70-74.ZHAO Jun，ZHAN Peipei，CAO Hongqiang.Prediction of processing parameters about roundness bend correcting technology for steel pipe［J］.Materials science＆ technology，2010，18(1):70-74.

［15］ZHAO Jun，ZHAN Peipei，MA Rui，et al.Control strategy of over-bending setting round for pipe-end of large pipes by mould press type method［J］.Trans.Nonferrous Met.Soc.China，2012，22:329-334.