MEO卫星相对相位自主保持策略
2014-09-15王洋刘莹莹黄河周军
王洋, 刘莹莹, 黄河, 周军
(西北工业大学 精确制导与控制研究所, 陕西 西安 710072)
0 引言
完全自主轨道保持可以有效降低卫星的运行成本,提高卫星应对突发事件的能力[1]。我国研发的二代北斗导航星座由MEO,GEO,IGSO三种卫星组成,其中MEO卫星多达24颗,如果能够实现MEO卫星的自主轨道保持,则可以极大地提高星座的工作能力,同时降低维护成本。具有完全自主轨道保持能力的卫星必须具有完全自主的导航与轨道控制。
天文导航是真正意义上的完全自主导航,轨道外推导航或者GPS导航都不是完全的自主导航。轨道外推导航需要定期注入轨道初值,所以不是完全的自主导航,GPS卫星BLOCKⅡR利用轨道外推的方式进行自主导航,可以实现180天用户测距误差优于6 m,缺点是在无地面站导航数据的情况下,缺乏时间基准,误差不断累积,难以实现长时间自主运行[2]。GPS导航受制于GPS系统,也不是完全的自主导航方式,且主要适用于LEO轨道[3]。天文导航虽然是完全自主导航,但是精度低,位置误差接近1 km(1σ)[4],PRISMA项目中利用高精度GPS导航实现自主轨道保持,导航的位置与速度误差分别优于10 cm(1σ)与1 mm/s(1σ)[5]。
国内外对于自主轨道控制也进行了许多的研究,Mclnnes提出了一种基于位函数的环状星座自主轨道控制方法[6],这种方法的缺点是推力器需要产生连续的推力。Junhua Xiang等提出了一种利用轨道要素之间的线性关系,间接补偿相位以及升交点赤经的漂移[7],但是并未讨论导航误差以及初始入轨偏差的影响。
本文对二代北斗导航星座中MEO卫星相对相位的自主轨道保持问题进行了研究。在分析摄动影响的基础上,通过相位的变化量间接求取轨道长半轴偏差,克服低精度的天文导航对轨道控制的影响,采用间接求取的长半轴偏差进行轨控,可以有效消除相对相位的漂移。
1 相对相位演化
a,e,i,Ω,ω,M为开普勒轨道六要素,下面轨道根数如无特殊说明,皆指平轨道根数。设tk时刻,卫星i的轨道相位角为λik,平近点角为Mik,近地点角距ωik,则对于卫星1和2,设t2>t1,分别有:
(1)
对于MEO卫星摄动运动而言,只有长期变化才会引起卫星轨道构型的根本变化,太阳光压主要引起周期变化,下面研究地球非球形与第三引力体引起的长期摄动变化,设Mec与Mtc分别为地球非球形摄动与第三引力体引起的平近点角长期变化率,ωec与ωtc分别为地球非球形摄动与第三引力体引起的近地点角距的长期变化率,由文献[8]可知,对于小偏心率轨道有:
(2)
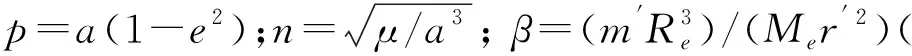
不考虑入轨偏差时,相对相位变化量Δλ为:
Δλ=(λ21-λ11)-(λ20-λ10)
=(λ2c-λ1c)(t1-t0)
(3)
式中,λ2c和λ1c为相位角长期变化率。
由文献[8]可知,对于MEO卫星,长半轴a以及轨道倾角i无长期变化,则由式(2)可知,同一MEO轨道面的卫星,Mtc,ωtc,Mec以及ωec是相同的,即λ2c与λ1c相同。长期来看,空间摄动不会引起相对相位的长期变化。考虑卫星存在入轨长半轴偏差Δa,相应的轨道角速度偏差为Δn。
Δλ=Δn(t1-t0)
(4)
因此,相对相位控制的目标就是消除初始入轨长半轴偏差。
2 相对相位自主控制
2.1 自主轨道控制面临的问题
卫星的初始瞬时轨道根数为:i=55°,Ω=30°,a=27 732.14 km,ω=30°,e=0.004 8,u=0°。
天文导航只能测量出位置与速度信息,需要研究轨道根数的误差分布,假设位置与速度的误差标准差分别为1 km与0.1 m/s[4],经过l=20 000次蒙特卡洛法实验,可得长半轴a的误差分布δa0如图1所示。对数据进行迭代统计[9],得到各个瞬时轨道根数的误差标准差与误差均值如表1所示。
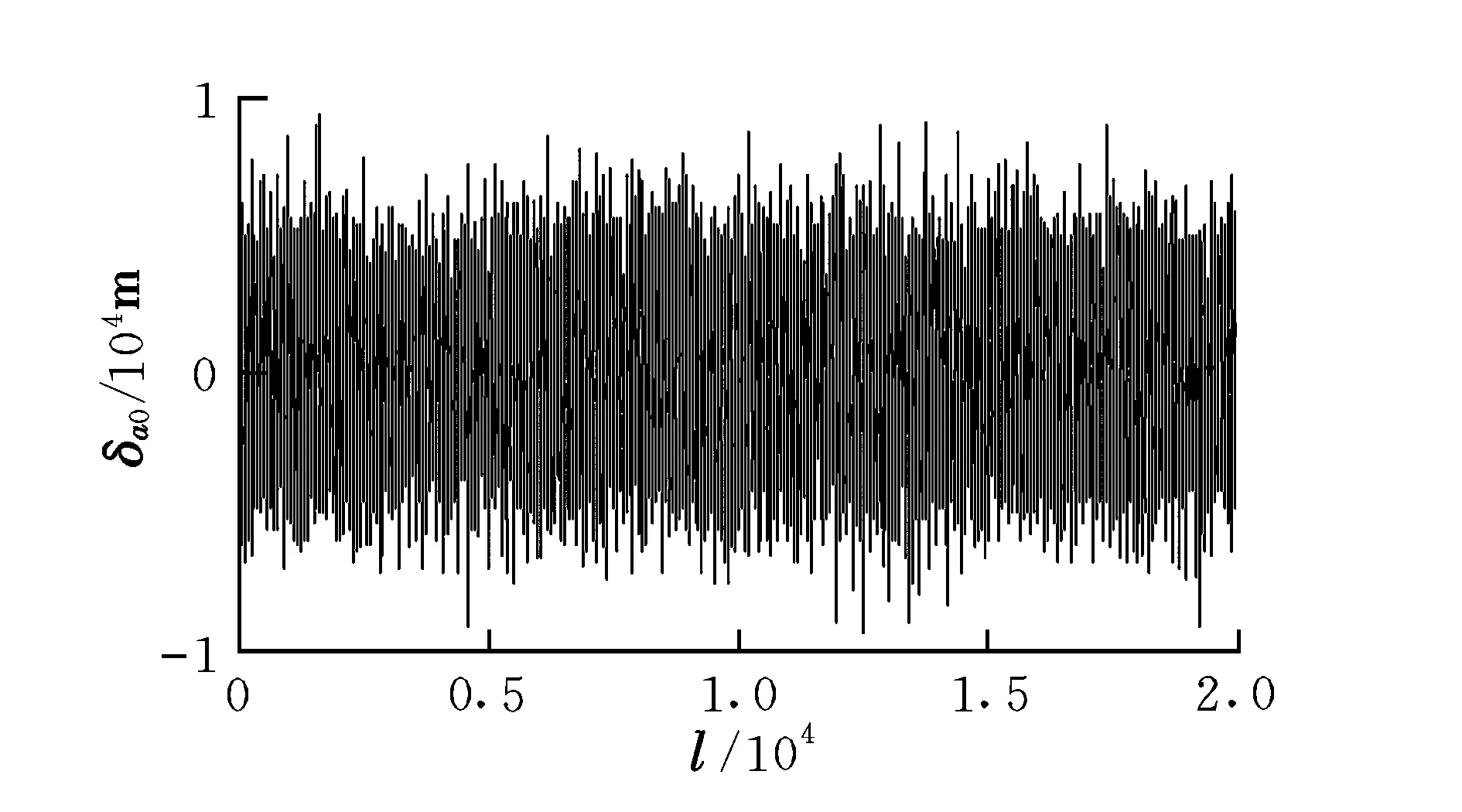
图1 轨道根数误差Fig.1 Orbit element error
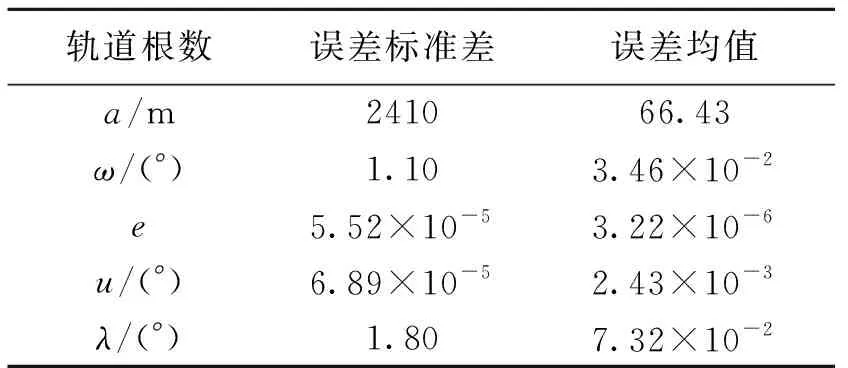
轨道根数误差标准差误差均值 a/m241066.43ω/(°)1.103.46×10-2e5.52×10-53.22×10-6u/(°)6.89×10-52.43×10-3λ/(°)1.807.32×10-2
对于卫星i与卫星j,其长半轴分别为ai和aj,轨道角速度分别为ni和nj,长半轴偏差Δaij=aj-ai,轨道角速度偏差Δnij=nj-ni。卫星i为标称轨道,则有如下关系存在[10]:
(5)
由表1可知,在天文导航情况下,长半轴a的误差标准差达到2 km以上,而当ai=27 730.14 km,Δaij=1 km时,相对相位漂移高达每年13°。如果直接采用天文导航所得到的长半轴偏差进行控制,则相对相位会在短时间内迅速漂移,这样将会加大控制燃料的消耗与控制的频率,无法保证卫星的长期轨道保持的要求。
2.2 相对相位自主保持方案
设tk时刻,卫星i的偏近点角为Eik,纬度俯角为uik,真近点角为fik,轨道周期为Ti,不失一般性,取卫星1和2,通过控制卫星2来控制相对相位,Δλ为相对相位角差,ΔE为相对偏近点角差,Δu为相对纬度幅角差。定义如下:
(6)
由式(5)可得:
(7)
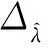
下面证明当t1-t0=NT1(N=1,2,…)时,有Δu≈ΔE成立,由轨道力学有:
ΔE-f(e,E)=Δn12NT1
(8)
其中:
ΔE=(E21-E11)-(E20-E10)
f(e,E)=e[(sinE22-sinE21)-
(sinE12-sinE11)]
由于t1-t0=NT1,则E21≈E20,且E11=E10,则f(e,E)≈0,所以有:
ΔE≈Δn12NT1
(9)
同时,考虑t0到t1时间较短,假设近地点角距ω未发生变化。
Δu-ΔE= (f22-E22)-(f21-E21)+
(f11-E11)-(f12-E12)
≈0
(10)
则可知Δu≈ΔE。
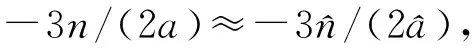
(11)
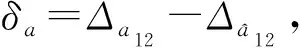
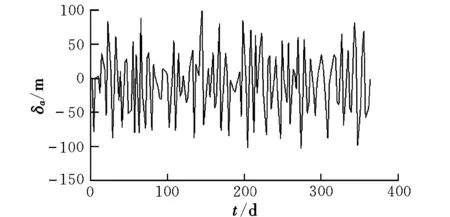
图2 估计误差Fig.2 Estimation error
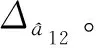
GPS卫星也是MEO卫星,其地理经度的控制采取了极限环的控制策略,通过极限环实现地理经度的稳定[11-12],考虑设计合适的极限环实现相对相位的稳定。
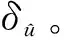
长半轴的控制量为f,控制之前的长半轴为a0,则控制之后的长半轴a1=a0+f。其中f由下式给出:
(12)
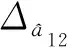
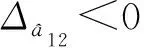
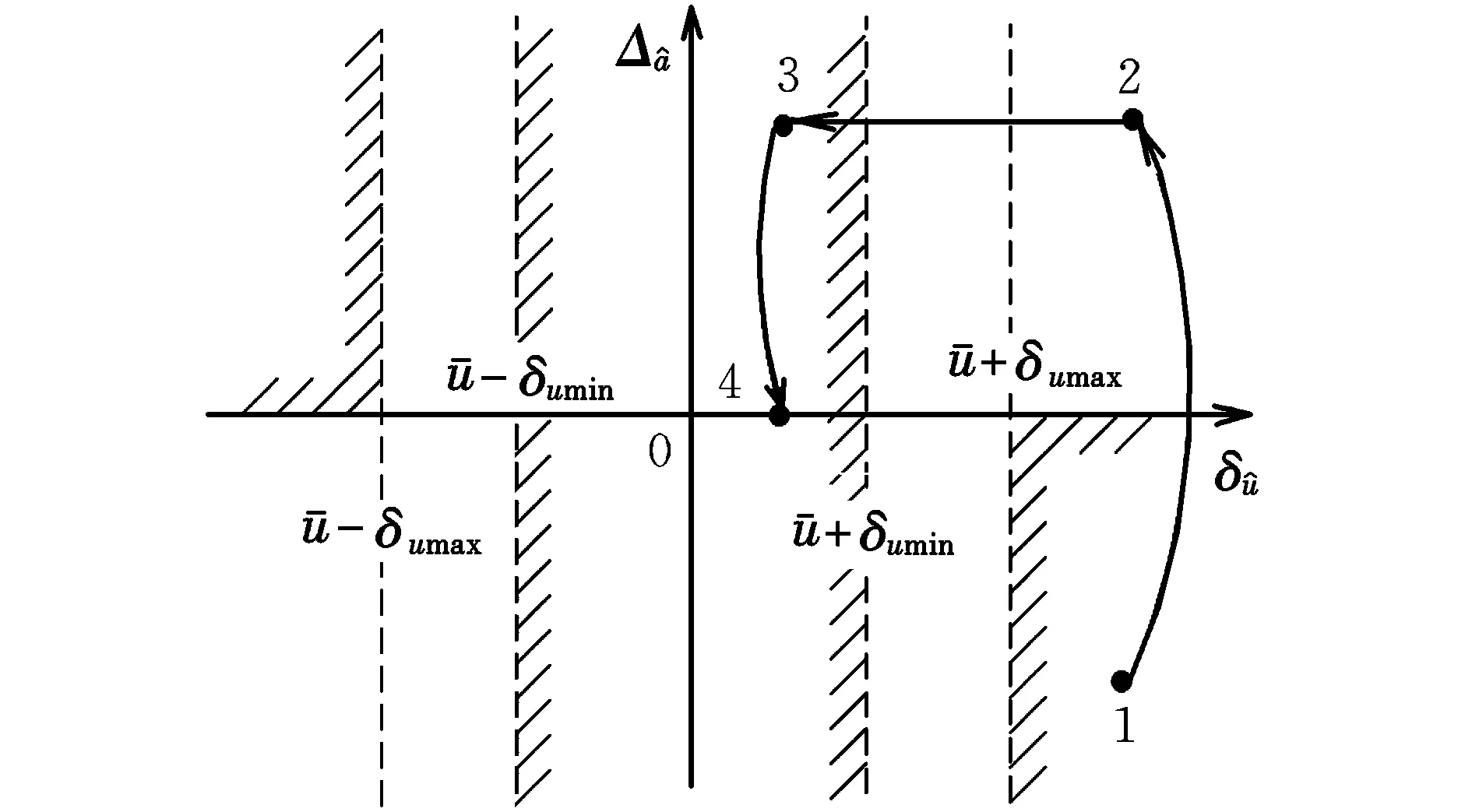
图3 控制相位图Fig.3 Diagram of phase control
3 仿真算例
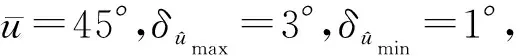
长半轴的控制量由式(12)给出,Ft如图4所示,其中第1次推力器喷气时间为21.26 s,第2次为15.19 s。由图5给出真实的长半轴偏差Δa12。设tk时刻,卫星1与卫星2的相位角差δλ=λ2k-λ1k。由图6给出δλ。
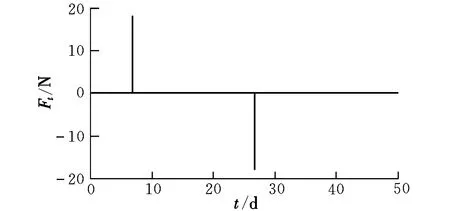
图4 切向控制力Fig.4 Tangential force

图5 长半轴偏差Fig.5 Semimajor axis deviation
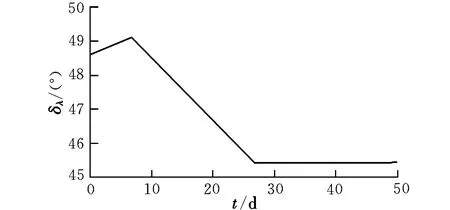
图6 相位角差Fig.6 Phase angle difference
4 结束语
本文研究了北斗导航星座的MEO卫星相对相位的完全自主保持问题,在分析相对相位漂移的基础上,考虑到天文导航低精度的特点,设计了一种间接求取长半轴补偿量从而实现相对相位稳定的轨道控制策略。仿真验算证明,在长半轴导航误差标准差高达2 410 m的情况下,采用所设计的控制策略仍然能够有效地实现相对相位的长期稳定控制,说明该策略完全能够满足MEO卫星相对相位自主保持的要求。
文中采用估计精度较高的纬度幅角u代替相位角λ设计控制律,在小偏心率的MEO轨道中效果良好,以后研究的重点是如何解决大偏心率下的相对相位自主保持问题。
参考文献:
[1] Conger R E,Gurevich G,Werts J R.Autonomous on-board orbit control[R].AIAA-2002-1976,2002.
[2] 陈忠贵,帅平,曲广吉.现代卫星导航系统技术特点与发展趋势分析[J].中国科学,2009,39(4):686-695.
[3] 秦红磊,梁敏敏.基于GNSS的高轨卫星定位技术研究[J].空间科学学报,2008,28(4):316-325.
[4] 宁晓琳,马辛.地球卫星自主天文导航滤波方法性能分析[J].控制理论与应用,2010,27(4):423-430.
[5] D’Amico S,Ardaens J S.Spaceborne autonomous formation-flying experiment on the PRISMA mission [J].Journal of Guidance, Control,and Dynamics,2012,35(3):834-849.
[6] Mclnnes C R.Autonomous ring formation for a planar constellation of satellites[J].Journal of Guidance,Control,and Dynamics,1995,18(5):1215-1217.
[7] Xiang Junhua,Zhang Yulin.Design and simulation of autonomous control system of satellite[C]//First International Conference on Innovative Computing,Information and Control.Beijing:IEEE,2006:109-112.
[8] 刘林. 航天器轨道理论[M].北京:国防工业出版社,2000:99-270.
[9] 李新国,方群.有翼导弹飞行动力学[M].西安:西北工业大学出版社,2004:129-135.
[10] 胡松杰,申敬松,郇佩.基于参考轨道的Walker星座相对相位保持策略[J].空间控制技术与应用,2010,36(5):45-49.
[11] Bob E S,Graig D E.GPS orbit evolution:1998-2000[R].AIAA-2000-4237,2000.
[12] Bob E S,Giorgio E O G.Decade-scale GPS orbit evolution and third body perturbations [R].AIAA-2008-7070, 2008.
