驾驶员最优控制模型的应用研究

薛红军, 巫火根, 张晓燕, 张峰

(西北工业大学 航空学院, 陕西 西安 710072)

0 引言

人机系统工程是以控制论、模型论和优化论为基础的综合性边缘技术学科,建立科学、准确的人的数学模型是人机工程学研究的重点[1]。人的数学模型建立方法有多种,随着控制理论的发展而不断发展,由基于早期的经典控制理论的驾驶员传递模型到基于现代最优控制理论的驾驶员最优控制模型,相继又出现了模糊控制、鲁棒控制、预见预测控制和智能控制模型。通过对驾驶员控制决策特性的进一步研究,又有了驾驶员的最优鲁棒控制模型、预见预测控制模型以及基于神经网络的驾驶员模型。20世纪60年代末到70年代初期,Kleinman等[2]依据随机最优控制(LQC)理论提出了驾驶员最优控制模型(OCM),随后又出现了改进后的OCM模型,如1976年建立的HOCM模型[3],1979年建立的LQOCM(LQG-OCM)模型,1992年Davidson[4]在HOCM和LQG-OCM模型的基础上又建立起来了MOCM(MODIFIED-OCM)模型,1994年Edkins[5]建立了SOCM(SUB-OPTIMAL PILOT MODEL)模型,这些模型既可以实现单轴任务的分析研究,也可以实现对多轴多环的复杂控制任务的研究。

本文通过建立驾驶员的MOCM模型,形成人机闭环仿真系统,分析人机系统的飞行品质,并将其与试验中驾驶员的Cooper-Harper评价尺度(PR)进行对比分析,验证驾驶员最优控制模型的有效性和准确性。本文主要针对驾驶员最优控制模型的应用进行了分析研究。

1 MOCM数学模型

驾驶员最优控制模型基于如下假设:受过良好训练的驾驶员能够以一种近似最优的方式控制系统,在其自身的极限能力内调整增益和补偿量,以最小化一个客观的评价函数并给出其主观评分[6]。MOCM的结构如图1所示。

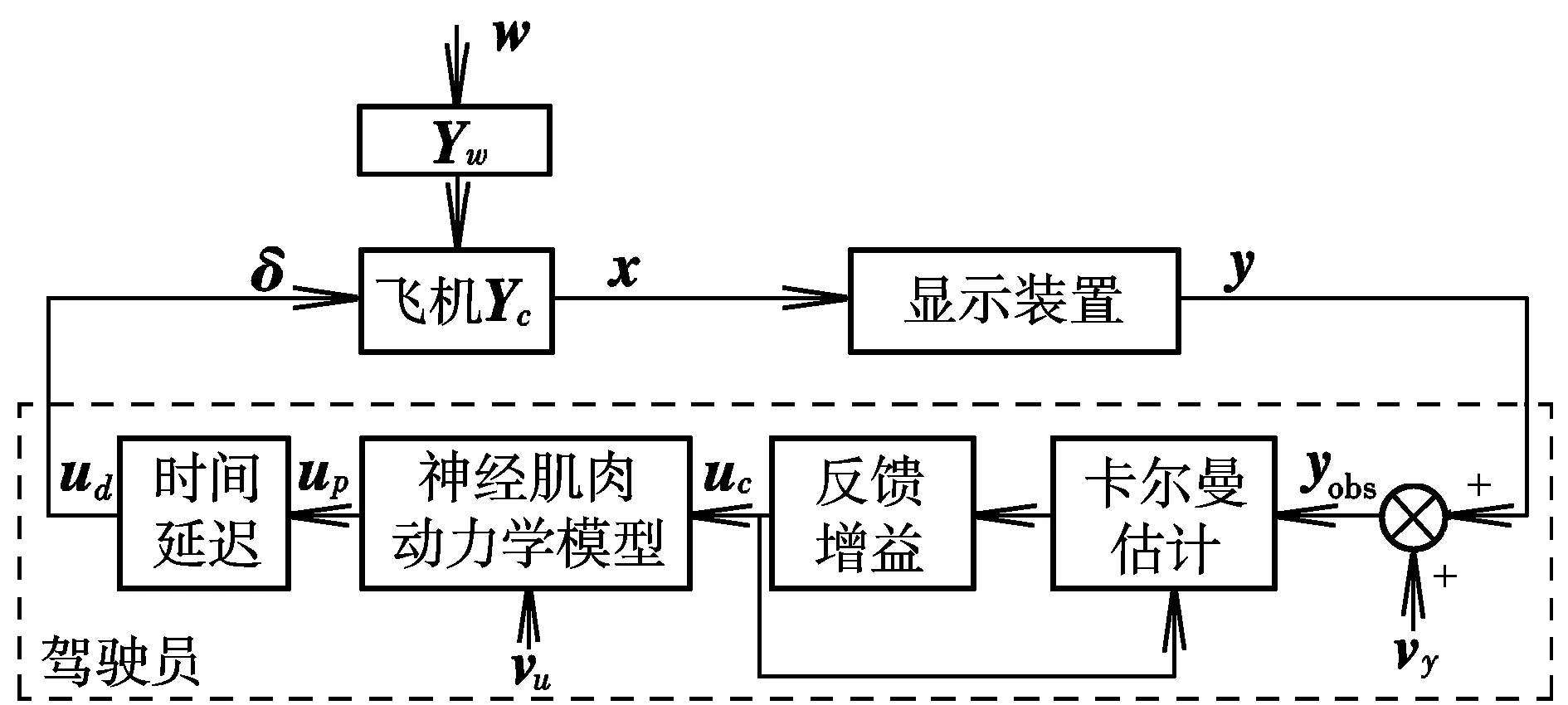
图1 MOCM结构框图Fig.1 Structure of MOCM

飞机的动力学模型状态是可控的,被控对象带扰动的动力学常系数空间状态方程如下[7]:

(1)

式中,x为n维状态向量；δ为驾驶员模型的nu维输出状态向量;w为协方差W的nw维零均值高斯白噪声;y为驾驶员模型的nv维输入状态向量。驾驶员的延迟时间用二阶Pade近似替代(因为在驾驶员感兴趣的频率范围(0.1～10.0 rad/s)内，二阶Pade近似可以很好地等效纯延迟e-τs)。

(2)

将式(1)和式(2)结合可得:

或

控制任务的要求是使得二次性能指标Jp最小。

(Qy≥0,r≥0,f>0)

定义新的状态变量χT=[xup]T,得到新的增广状态空间方程如下:

或

应用LQG理论可以得到增广状态矩阵方程的最优全状态反馈增益为:

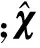
(A0)TK+KA0+Q0-KB0f-1(B0)TK=0

神经肌肉动力学模型由下式决定:

因此可以得到:

考虑到人操纵输入的不确定性,加入了控制噪声vu。

式中,vu为零均值协方差Vu的高斯白噪声。从而可以得出下面新的增广矩阵:

或

状态估计由Kalman滤波得到:

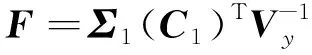
A1Σ1+Σ1(A1)T+W1-

W1=diag(WVu),W≥0,Vu≥0

整个人机闭环系统的状态方程为:

I1=[Ip0],Cδ=[0Cd1]

驾驶员的状态空间方程为:

或

根据Lyapunov方程,可以求出状态向量的协方差值P。

yT=[yobsδ]T的协方差按下式计算:

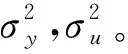
2 MOCM模型的仿真应用

2.1 试验介绍

本文采用的试验数据就是在LAMARS模拟器上完成的。根据文献[8],试验中对飞机施加的干扰信号为正弦函数的叠加(Sum-of-Sines)信号,这种信号的数学模型如下:

任务由13个正弦函数组成,相角φi随机选择,任务增益K根据所需任务幅值来确定。ωi在0.1～30.0 rad/s之间线性分布,Ai取值为2 rad/s,最终俯仰角的干扰信号如图2所示。

图2 俯仰角干扰信号Fig.2 Driving noise of pitch angle

图3所示是提供给驾驶员完成补偿控制任务的误差信号的显示器。图中,θe为俯仰角误差,φe为滚转角误差。本次试验中只关注俯仰角误差,因此驾驶员的任务就是在飞机受到干扰的情况下让θe尽可能为零。

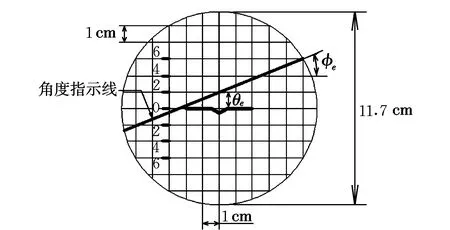
图3 补偿信号显示器Fig.3 Compensation signal display

以5个比较典型的飞机俯仰角传递函数为例[8],应用驾驶员最优控制模型对飞机飞行品质等级进行评估,与真实的驾驶员给出的主观评价作比较。5个飞机的传递函数如下:

第1个传递函数与积分环节非常接近,可以当作积分环节来处理,其它4个的特性如表1所示。

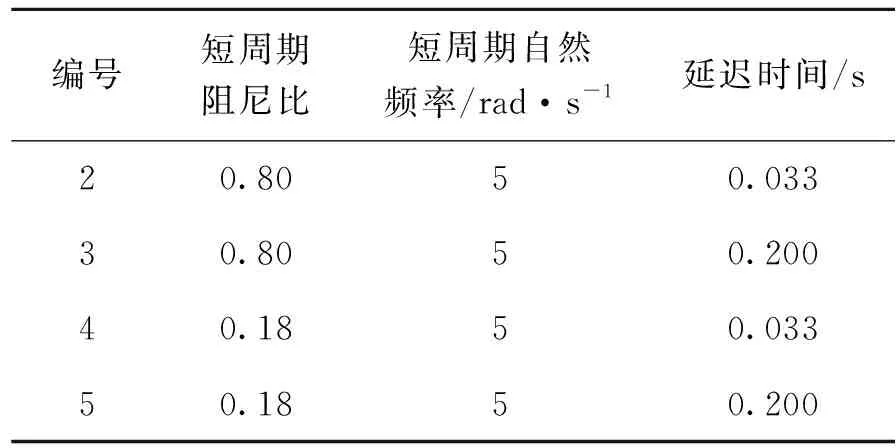
表1 飞机的动力学特性Table 1 Aircraft dynamics

这5个模型很好地代表了一般飞机的传递函数,覆盖的飞机动力学模型范围比较广,每一种情况都由6名不同的驾驶员来完成评价,然后取其给出PR值的平均值,如表2所示。

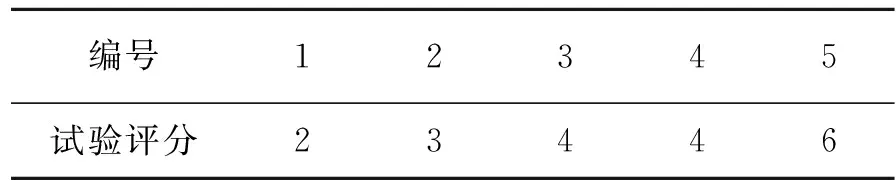
表2 试验的Cooper-Harper评分(PR)Table 2 Cooper-Harper ratings of test

从表2中可以看出,编号为1和2的飞机飞行品质等级为1级,编号为3～5的飞机飞行品质等级为2级。

2.2 模型参数

在LAMARS飞行仿真模拟器上的追踪信号f(t)是正弦函数的叠加信号,可以用高斯白噪声经过滤波器的有色噪声来模拟。

有色噪声的输入形式有3种,分别加在飞机动力学模型的输入端、输出端和中间,如图4～图6所示。根据试验中的实际情况,本文加在输出端。

图4 噪声加在飞机输入端Fig.4 Noise injected at aircraft input end

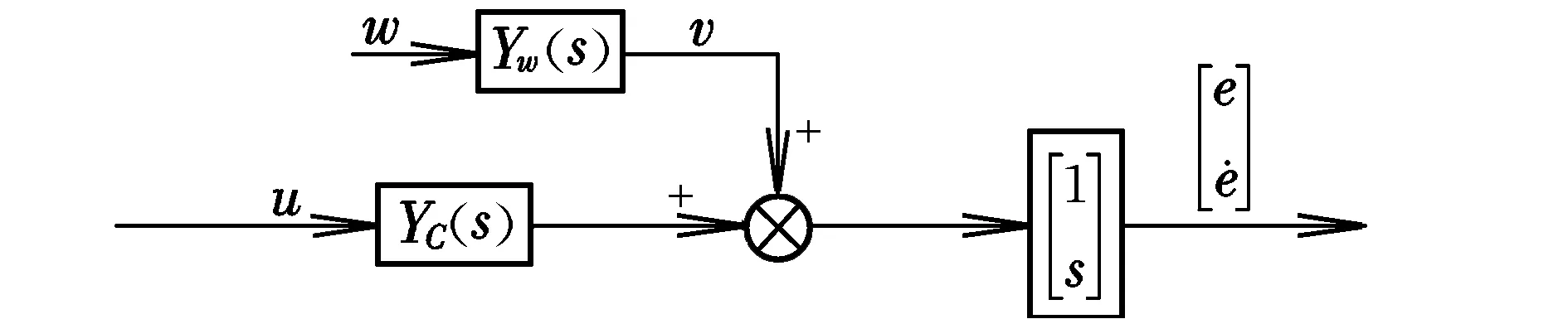
图5 噪声加在飞机输出端Fig.5 Noise injected at aircraft output end

图6 噪声加在飞机中间Fig.6 Noise injected in the middle of the aircraft

对于单轴任务,Vy和Vu由下式求得:

式中,ρy和ρu为噪信比,需要先给定,ρy的取值与显示器、驾驶员自身因素以及驾驶环境有关,最终通过迭代计算让噪信比达到给定的值,此时的Vy和Vu就是所需要的噪声强度。驾驶员Cooper-Harper评分与性能指标之间的关系式为:

式中,ωw为滤波器的带宽。

2.3 仿真计算结果及分析

根据表3给定的参数,基于MOCM模型建立人机闭环系统,利用驾驶员Cooper-Harper评分与性能指标之间的关系式得到计算结果,如表4所示。通过与表2的试验结果相比较可以看出,仿真计算结果与试验结果非常接近。

表3 MOCM模型参数Table 3 Parameters of MOCM

表4 仿真的Cooper-Harper评分(PR)Table 4 Cooper-Harper ratings of simulation

由系统仿真得到驾驶员的MOCM最优控制模型描述函数为:

YP1=δ/e=

YP2=δ/e=

YP3=δ/e=

YP4=δ/e=

YP5=δ/e=

3 结束语

本文对5个飞机的动力学模型建立了人机闭环系统,得到了驾驶员的MOCM最优控制模型,最后利用相关计算指标得到了驾驶员的Cooper-Harper评价尺度。经过比较可知,计算结果与试验结果相一致。结果表明,此方法可以应用到人机系统的飞行品质分析中,在飞机设计的初期就可以对飞机的性能做出评估。本文只针对驾驶员的单轴操纵任务建立了人机闭环系统模型,以后还需要对多轴任务作出应用研究。当被控对象难以控制时,模型预测与真实驾驶员评价的一致性会差一些,就需要对驾驶员Cooper-Harper评分与性能指标之间的关系式进行修正,从而建立更准确的关系式,这需要大量的试验数据作支撑,这也是下一步的研究方向。

参考文献：

[1] 徐浩军,刘东亮,孟捷.基于系统仿真的飞行安全评估理论与方法[M].北京:国防工业出版社,2011:7.

[2] Kleinman D L,Baron S,Levison W H.An optimal control model of human response-part I:theory and validation[J].Automatica,1970,6(3):357-369.

[3] Toader Adrian,Ursu Ioan.PIO I-II tendencies,part 2:improving the pilot modeling[J].INCAS Bulletin,2011,3(1):109-118.

[4] Davidson J B,Schmidt D K.Modified optimal control pilot model for computer-aided design and analysis[R].NASA-TM-4384,1992.

[5] Edkins C R.The prediction of pilot opinion ratings using optimal and sub-optimal pilot models[R].AD-A278679,1994.

[6] 胡兆丰.人机系统和飞行品质[M].北京:北京航空航天大学出版社,1994:39.

[7] Toader Adrian, Ursu Ioan.PIO I-II tendencies case study,part 1:mathematical modeling[J].INCAS Bulletin,2010,2(1):91-102.

[8] Edkins Craig R.Human pilot response during single and multi-axis tracking tasks[R].AD-A275080,1993.