开关磁阻电机的模糊自适应简化控制

马云龙，章 玮

(浙江大学电气工程学院，浙江杭州310027)

0 引 言

近年来随着电力电子和微电子技术的发展，开关磁阻电机(SRM)越来越受到关注。相对于其他电机，其具有结构简单、成本低廉、运行可靠、调速范围广、各相独立等特点，在航空、汽车等领域得到了大量应用。但是由于SRM特有的开关特性，在运行过程中伴随着较大的转矩波动，由此产生的严重的噪声和振动会对SRM的应用产生较大的制约［1-3］。因此，国内外学者都对SRM的控制策略进行了很多研究。

模糊控制是一种不需要了解被控对象精确数学模型的智能控制方法，对被控对象参数变化不敏感，非常适合应用于SRM的控制。针对SRM的特点，学者们进行了很多关于模糊控制的研究，文献［4］研究了一种查表方式的模糊控制，在低成本的单片机上也有较好的性能;文献［5-6］对模糊PI控制进行了研究，得到了较好的性能。上述方法的模糊规则一旦选定无法更改，而模糊自适应能够根据不同场合实现在线改变模糊规则，该方法的核心在于校正因子的选择，对于校正因子的选择，文献［7-8］分别采用了遗传算法和神经网络算法，都有很好的动态和静态响应;文献［9］中提出了一种校正因子进行模糊计算的方法，有较好的响应性能。但是上述方法在线改变模糊规则的同时，带来了较大的计算量，给模糊自适应的实现带来了困难。

本研究结合模糊自适应方法，讨论自适应因子对控制的影响，提出一种简化的校正因子选择方法，实现根据特定场合在线改变模糊规则，通过仿真和实验验证模糊自适应控制方法对SRM调速控制具有良好的性能。

1 开关磁阻电机控制模型

1.1 系统框架

以8/6为例的SRM控制框图如图1所示，基本的控制方法采用PWM斩波控制。

图1 SRM控制框图

为了使控制更灵活，变频器拓扑结构采用四相不对称半桥结构，不对称半桥拓扑如图2所示。

图2 不对称半桥拓扑

1.2 模糊控制器设计

模糊自适应控制框图如图3所示。模糊自适应控制基本结构采取双输入单输出的方式，其中输入量为误差E，误差的变化量EC，输出U，校正因子α。根据系统控制的要求选取不同的α，可以实现在线对模糊规则表的改变。

图3 模糊自适应控制框图

模糊化的过程主要是将精确的输入量转化为模糊控制识别的模糊子集中。这里E、EC、U整数化的论域为{±7，±6，±5，±4，±3，±2，±1，0}。当输入量被转化到模糊论域后，需要转化到模糊子集才能进行模糊推理，此处E、EC、U 都采用7档，即{负大(NB)，负中(NM)，负小(NS)，零(Z)，正小(PS)，正中(PM)，正大(PB)}，模糊子集可以通过隶属度函数描述，采用的三角形隶属度函数如图4所示。本研究采取的模糊推理方式为Mamdani模糊推理方法。

图4 隶属度函数

带有校正因子的模糊规则一般可以用下式的控制规则表示:

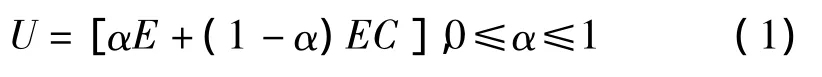
输出量对计算结果进行取整运算，式中的α称为校正因子，通过改变α的值，可以改变偏差和偏差变化的不同加权程度，避免规则定义中过大的不平滑性［10］。对于SRM的运行，由转矩平衡式可知:

在启动或者大范围速度变化时，调节器输出指令电流Ι*一般输出值较大，导致输出电磁转矩Te较大，而摩擦阻力Βω和负载转矩TL的影响较小，加速过程可视为匀加速，而转矩脉动对转矩影响较小可视为有较大的E而EC近似不变，最优的控制量应选择较大的α值，随着转速的升高，误差Ε也在减小，控制量的α值不再增加，此过程中最优α可以近似与E呈线性关系;而在稳态运行时，Te可视为恒定值，而实际转矩会由于SRM的开关特性有一定抖动，可视为扰动量ΔTe，转矩平衡式中其他量基本不变，因此，稳态运行时影响控制量较大的是EC，应选用较小的α值，为了简化运算，可认为最优的α值与EC呈线性关系，由此当扰动出现后α值变小，并保持该值。同时为了避免模糊规则表频繁改变，需要在变化中设置阈值，并且采用增量的形式，具体的表达式如下式所示:

式中:k1，k2—需要保证校正因子的增量在0～1之间;σ，δ，ε—误差和误差偏差量的门阈值;α(0)—可以设为0.5。

此时的模糊规则表如表1所示。

表1 α=0.5时模糊规则表

本研究解模糊采用的是重心算法，即取隶属度函数曲线在连续域上与横轴所包围的面积的重心为模糊推理的输出值，如下式:

式中:μ(ui)—输出元素的隶属度函数，ui—输出函数的语言值。

2 仿真和实验结果

2.1 仿真验证结果

为了验证前述方法的正确性，本研究分别采用仿真和实验的方法对SRM进行调试。仿真采用Matlab的Simulink组件，被控对象为一台8/6的开关磁阻电机，驱动器采用四相不对称半桥。

仿真时设定条件如下:

开通角0°;关断角30°;给定转速为500 r/min;分别采用 α =0.2，0.8 和 f(E，EC)，α =f(E，EC)为式(3)所给定函数。

其中，3种情况进行启动时不同α速度响应如图5所示。由图5可以发现，在启动时由于误差较大，对控制起主要影响的是E，因此α=0.8的速度响应速度最快，而 α=0.2的上升最慢，而 α=f(E，EC)性能介于二者之间。

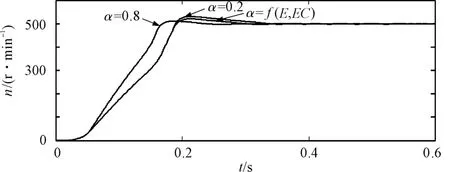
图5 启动时不同α速度响应

为了验证不同α值对突加负载的响应，设置在稳定运行在500 r/min时，电机突加突卸负载时转速波形如图6(a)所示，突加负载时转矩响应放大如图6(b)所示。从图6中可以发现，使用变校正因子的方法能够对扰动有很好的抑制作用。

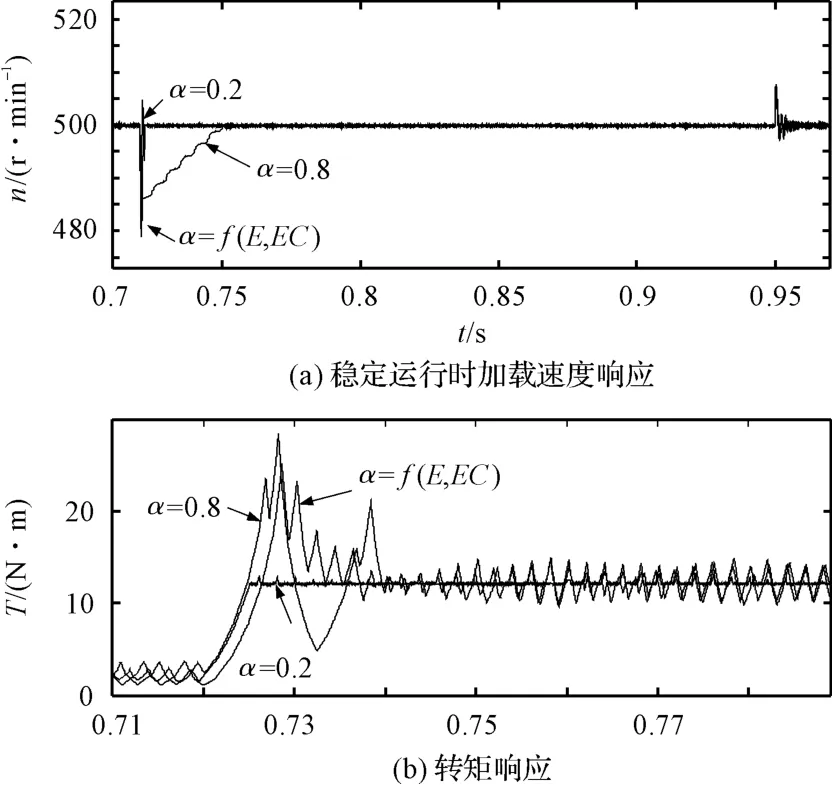
图6 稳定运行时加载速度的响应及转矩响应

2.2 实验验证结果

实验采用8/6四相SRM，不对称半桥驱动电路。电机最大电感0.226 03 H，最小电感0.028 65 H，最大磁链为0.273 44 Wb，额定转矩 0.95 N·m，额定转速1 500 r/min，额定电压132 V，额定功率150 W，控制芯片采用 TI公司的 TMS320F28335，光栅码盘线数为2 500线，4倍频后使用。

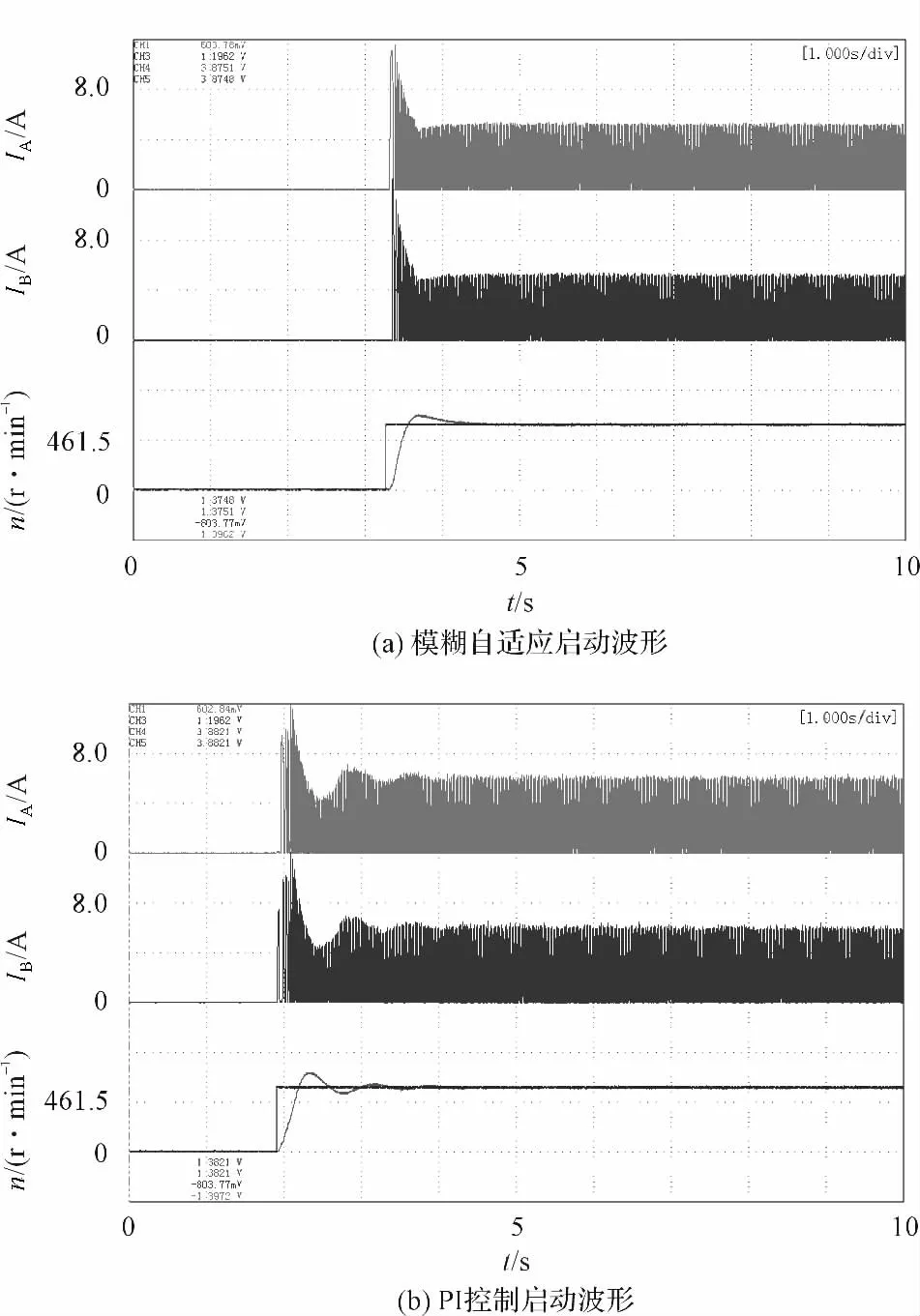
图7 模糊及PI波形

实验时，母线电压为30 V，从静止开始空载给定转速600 r/min，其中速度给定和速度响应曲线采用DA输出滤波后显示，示波器截屏的时间刻度都为1 s/div。PI控制的速度给定及响应曲线和A、B两相的电流波形如图7(a)所示，带有校正因子的模糊控制波形如图7(b)所示。突加突卸负载时模糊自适应和PI控制的波形如图8(a)、8(b)所示。对比可以发现模糊自适应方法具有较好的动态和静态响应。

图8 模糊自适应及PI控制突加突卸负载

3 结束语

针对SRM运行中的非线性和强耦合现象，本研究将模糊自适应控制应用到SRM调速控制中，通过仿真和实验，验证了带有校正因子的模糊自适应方法在SRM调速系统中有较好的动态和静态响应性能，对运行中开关特性造成的转矩波动有一定抑制作用。简化的校正因子选择方法兼顾了运算量和性能，实现了不同运行条件下的平稳切换。研究人员可以根据变化的需求，改变校正因子变化的系数，避免了模糊规则变化过快或者过慢的情况。同时笔者根据实际使用的情况设置了误差限，以避免采样等问题产生的小误差而引起系统的振荡现象。

［1］王宏华.开关型磁阻电动机调速控制技术［M］.北京:机械工业出版社，1995.

［2］吴建华.开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000.

［3］吴红星.开关磁阻电机系统理论与控制技术［J］.北京:中国电力出版社，2010.

［4］王宏华.SR电机模糊控制器设计研究［J］.中小型电机，2000，27(6):26-30.

［5］TAHOUR A，AISSAOUI A G，MEGHERBI A C.Fuzzy PI control through optimization:A new method for PI control of switched reluctance motor［C］//Complex Systems(ICCS)，2012 International Conference on.Singayore:［s.n.］，2012:1-7.

［6］孙建忠，白凤仙.基于DSP的开关磁阻电机调速系统的模糊控制［J］.电机与控制应用，2007，34(5):33-36.

［7］修 杰，夏长亮.基于遗传算法的开关磁阻电机自适应模糊控制［J］.电工技术学报，2007，22(11):69-473.

［8］MARSALINE B M，MARIMUTHU N S，SINGH N A.Optimizing the switching angles of SRM using adaptive neurofuzzy controller［C］//Information and Communication Technology in Electrical Sciences(ICTES 2007)，2007.ICTES.IET-UK InternationalConferenceon. 2007. Chennai，Tamilnadu，India:［s.n.］，2007:448-451.

［9］孙 丹，贺益康，智大为.基于非线性模型的开关磁阻电机自适应模糊控制［J］.电工电能新技术，2001，20(4):9-13.

［10］席爱民.模糊控制技术［M］.西安:西安电子科技大学出版社，2008.